随着供应链中信息化的不断加强,供应商和各销售商之间普遍建立了便捷而可靠的订单管理等信息系统,而各经销商之间往往数量众多且存在一定竞争性和信息壁垒,相互联系依然不是很普遍。在此情景下,如何通过供应商引导调整经销商之间的货物转运,实现供应链优化成为一个重要课题。以往学者也认为,通过库存共享(即独立经销商们对整个供应链进行协商转运)可为供应商和整个供应链带来库存汇集效应(inventory pooling effect),可有效减少经销商的库存量,节省供应商的生产及库存费用、避免浪费,也可更好更及时地满足市场消费需求。Singha等[1]比较了集中和分散供应链的优缺点。实践中,有供应商通过给经销商提供现金奖励等方式,鼓励存货在销售网络中共享及转运,但这需要所有经销商都参与到整个协调系统中来,现实中面临很多不确定性,因此较难操作。
Shao等[2]将分散型供应链系统分为横向分散型系统(即经销商之间是相互独立的)、纵向分散型系统(即经销商均独立于供应商)和完全分散型系统(即横向、纵向都分散的系统)。多数研究都围绕横向分散型系统进行,根据经销商之间的合作程度可将协调策略分为转运价格(TP)和利润分配规则(PA)两种,但以往研究通常只考虑了全部经销商参与而供应商未参与的部分供应链,且采用较简单的单周期模型。本研究提出了一种供应商和经销商都参与的“纵向集中而横向分散”供应链模型,简称“半分散型”系统,且在双周期的情景下,该模型的库存转运优化如何进行?供应商及经销商在每个周期的最优决策是什么,如何设计双周期可变合同使供应商和经销商之间达到博弈均衡呢?这是本研究的重点。
双周期或多周期模型在现实中广泛存在,经销商们在收到第一批货物并销售一段时间后,会面临需要补货或者退回多余订货的情况,需要在第2周期进行库存调整,但调整依据是供应商和经销商之间签订的可调节供货协议。供应链协议调节模型此前由Li等[3]学者提出,并进行了动态理论分析;协议调节能否奏效的关键是经销商是否愿意接受协议,即每个经销商是否获得利益最大化的复杂博弈。因此,研究这类问题的关键便是供应商如何制定首次批发价格及再次采购价等,使得这一复杂博弈达到均衡。
1 文献分析库存分配及转运是供应链研究的一个热点问题。Agrawal等[4]学者研究了集中型供应链中的库存再分配问题,发现在一个分散型供应链里使用奖励措施才能实现库存的重新最优分配。国内方面,李晓宏等[5]研究发现在需求信息及时更新的情况下,转运可增加经销商及整个供应链的效益;李怡娜等[6]发现在供应商生产能力约束下,货物转运可缓冲市场波动风险,同时增加供应链的期望利润。这些研究集中于转运在特殊情形下对供应链个体及整体效益的影响,但未涉及如何设计转运机制以达到供应链均衡这一重要问题。
为实现供应链买卖双方的利益均衡,供应合同往往设定很多变量,如价格、数量、交货时间等可调整的参数,很多研究及实践中都常常提到这些特别的供应合同:如“采购折扣优惠合同”、退货合同、数量弹性合同、利润分成合同及期权合约[7]。此外,一些公司还采用供应合同组合,如惠普(HP)的合同组合主要考虑“价格优势”和“库存风险”的平衡点:50%采购签订长期合同,35%签订不具约束力的协议,15%为现货采购,提高灵活性。现货市场采购提供了理论上的库存控制灵活性,但其价格和产量的不确定性增加了供应的风险[8]。Agrawal等[4]考虑制造商可以选择短期和长期协议与供应合同,长期协议可缩短交货时间。Moinzadeh等[9]研究认为长期的供应合同的商品价格相对低一些,而短期合同的商品价格相对要高;Anupindi等[7]的研究涉及到同时采用几个供应合约的问题,每个合同指定一个价格,承诺每年最低采购数量和允许的最大年采购量。Anupindi等[7]研究的供货合同为:买方须提交最低累计数量的多期采购,而卖方给予买方一定的退货折扣价格优惠;Moinzadeh等[10]还研究了可调整的固定交货合同,当买方货物库存超过一定水平,在以后的采购中,买方被允许调整采购量。这些供应链研究不断引入变量进行探索,但其研究对象往往又是纵向的供应商和经销商之间的集中系统,未同时进行横向经销商(分散系统角度)的研究,存在一定局限性。
关于货物运转的理论模型,Rudi等[11]最先考虑了横向分散型系统的转运问题,提出一个单周期模型,假设只有两个经销商,转运仅发生在销售周期末,且经销商无条件接受任何转运价格,该研究证明存在唯一的纳什均衡订货数量并解出了转运价格函数。后续的相关研究多基于Rudi等的研究框架,如Hu等[12]利用类似模型证明了协调转运价格并不总是存在。钱宇等[13]重点研究了医药行业的供应链中转运订货和定价决策问题,结论为:转运虽然不能协调分散型供应链,但可以显著提高供应链效率。还有些研究考虑了横向分散型系统内假定经销商之间有部分合作,采用“PA”参与分配转运,并增加了所有经销商的总利润。Anupindit等[7]考虑了多个(超过两个)经销商的情况,假定经销商无权决定转运量,但有一个PA组合可以实现联盟博弈的一个核心(Core)均衡。Granot等[14]拓展了这项研究,放宽假设,允许经销商自主决定转运量。Huang等[15]比较了TP和PA两种方法,建议采用由一个中立的中心仓库来引导协调转运。近年来一些文献研究了横向分散型系统内非合作的经销商之间的部分协调转运问题。在Rudi等[11]研究的基础上,Yan等[16],以及Hanany[17]考虑在经销商之间信息不对称的情况下,需要一个中立的第三方来实现协调转运。但这些研究都忽略了第三方的利润诉求及是否愿意参与协调机制的问题。另外,陈敬贤等[18]利用数值分析研究了收益分享比例对协调供应链的作用。禹爱民等[19]的研究表明,在网络经销商与传统实体经销商竞争的情况下,转运虽不能完全协调分散型供应链,但在实体经销商的引导下,制定价格机制可实现经销商双赢。Dong等[20]研究了转运对纵向分散型供应链的影响,结合供应商的批发价格决策策略,比较完全分散型系统、纵向分散型系统的效率,但未考虑如何协调转运问题。以上这些研究都是单周期模型转运,Rong等[21]考虑了双周期模型,允许经销商在第2周期初作前瞻性的主动转运,证明了恒定的转运价格不能实现供应链协调均衡,Sharma等[22]还研究了多期间的模型,但这些研究又都没有考虑什么样的转运价格才能实现供应链的均衡。
现有的中外文献都集中于经销商之间的协商转运机制,尽管研究十分深入,但由于博弈理论分析难度过大,多数采用了单周期模型,通常也只针对经销商的部分供应链,这样的转运机制很难达成。本研究突破现有转运机制研究的局限,探索供应商通过可调节的供货协议引导经销商进行转运的机制,建立合理、严谨的双周期模型,分别求解完全集中型、半分散型系统模式下供应商和经销商的库存数量及价格的最优均衡决策。
2 模型构建 2.1 模型设定本研究先开发一个完全集中的分配供应链系统,这是一个可以实现最优生产和库存结构的分配与再分配动态系统模型。这里区分一下转运和再配送的定义,转运专门指经销商之间的货物流转,而再配送则是指供应商和经销商之间的发货与补货,供应商可能需要在发货之后给经销商再添补或接收退回货物。
假定一个供应商给n个均匀分布的经销商发货,用k表示某经销商,k= 1, …, n,用i表示发货的2个期间(i=1,2),用FX (·)表示随机变量函数X在概率空间(Ω, F, P)上的累计分布函数(cdf),其它相关设定如下。
Dki指经销商k在i期间的商品需求量(订货或供货量),其概率密度函数(pdf)为fi(s),累计分布函数(cdf)为Fi(s),s∈lR,方便起见,假定当s < 0时,fi(s)= 0。
hi是供应商和各经销商在每个周期的单位持有成本,假设供应商和经销商之间持有成本相等,本研究也将讨论供应商持有成本低于经销商持有成本的情况。
ci是第i期每单位商品的生产成本,假定c2-c1<h1,持有成本包括机会成本、仓储成本和物流成本。如果c2-c1<h1,经销商在第2期订货进行生产的成本c2比在第1期就生产好放入仓库产生的成本c1+h1更便宜。因此,这时供应商不会在第1期间进行过度生产并持有库存。
pi和ri是每个经销商在第i期间的单位处罚成本(违规退货、取消定单或合作解除的处罚价格)和单位收益,合理假定为ri+pi≥c2,否则第2期就不可能生产。经销商k在第1期中多余的需求量将会被积压,产生处罚成本p1;若第2期再定货,但经销商k不产生超额需求,处罚成本为p2。根据通常规律:设定基本成本价格中,处罚性价格pi是最大的,其次是滞销货物留在手上付出的单位成本hi;可变供应合同中,经销商对供应商增加货物(进货)的价格PBi要大于减少货物(退货)的价格PSi,因此有基本大小关系:
pi>hi;Pi>PBi≥PSi;而PSi与w(批发价)之间虽没有可比性,但通常w≥PSi。
设定v是供应链中在第2期末的单位商品残值,系统会产生残值,假设v≤(c1+h1+h2)∧(c2+h2)。
以上是本文涉及的基本数量关系,接下来构建模型将基于这些价格与成本之间的关系进行判断。
本研究的双周期过程设计为:在第1期(或在之前的某个时间开始1期,由于生产提前)开始时,供应商按单位成本c1生产,并分发给经销商(这期间供应商不持有库存)。在第2期的开始,客户的需求量发生不平衡变换:一些经销商可能不够销售需要加货,而一些又有剩余可能有低于最佳库存水平的需要调货出去。根据经销商的库存水平,供应商决定以单位成本c2产生并重新分配经销商之间的库存。重新分配库存完成,而且经销商第2期销售结束后,库存商品的残值为v/单位商品。
2.2 集中型供应链系统建模及分析研究将创建一个动态集中系统模型,先求解出这个系统在第2期间的最优生产和分销决策。然后再推导第1周期的最优决策,包括生产多少以及如何在经销商之间进行转运。
1) 第2期间的分析。
先定义Π2c(x)作为第2期间利润最大化的表达式,此时的库存函数为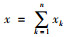
此时,xk表示经销商k的库存量,利润函数主要依赖于总需求库存水平x,而不是每一个经销商某时间的库存数量水平x1, …, xn,运输成本暂忽略不计。供应商在第2期间需决定是否再生产及产品在各经销商之间的分配数量,当经销商经过补货或退货之后,这个重新分配的库存数量zk可能大于或小于xk,但因货物若最终被退回的残值小于生产成本c2,所以供应商总设法在经销商之间进行调货,使其不退货给供应商,这里满足一个条件: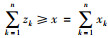
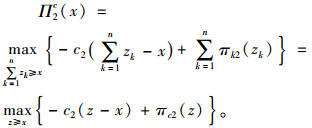
|
(1) |
这里,zk≥0,k=1,…,n,zk是经销商的库存分额,
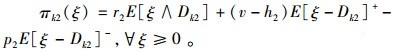
|
(2) |
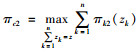
接下来讨论第2期的最优产量(Q)和最优再分配库存策略(ZQ0)的问题,此时有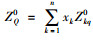

命题1 根据第2期间开始时的实际库存情况x∈lR,第2期间的最优产量及重新库存分配政策决定是:
(1) 当x < ZQ0,应该增加产量水平到ZQ0,分发给各经销商,使其库存水平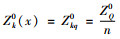
(2) 当x≥ZQ0,供应商不应该增加产量,而是通过集中系统在经销商之间进行调货,每个经销商的库存份额为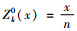
2) 第1期间的分析。
假定供应商开始时是0库存,其面临的总库存是各经销商库存之和。
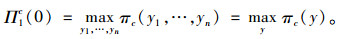
|
(3) |
对于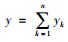
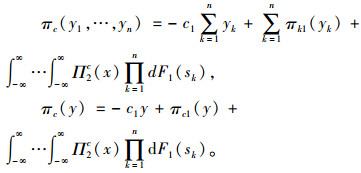
|
(4) |
此时,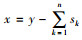
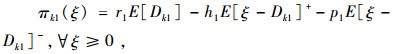
|
(5) |
并且
接下来讨论第1期的最优产量和最优再分配库存策略,假设产量为y,每个经销商的最优价值产量yk(k=1,…,n),其系统最大化的收益为πc(y),Y0为其间的最大产量的价值,有
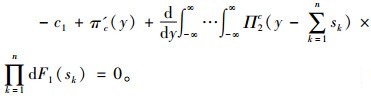
|
(6) |
命题2 供应商第1期间的最优产量是达到最大化的产量Y0并分发给各经销商。
2.3 半分散型供应链系统的库存再分配为了利润最大化,供应商在第1期间与经销商约定批发价格的同时,通过签订调整协议的方式鼓励各经销商在第2期间进行库存调整,进行加货或向其他经销商转移库存。其中,供应商与经销商之间用Stackelberg模型(Stackelberg game)进行分析,而经销商之间采用纳什均衡(Nash game)进行分析。
假设wk是经销商k从供应商那里获得商品的批发价,PkB和PkS分别是第2期间经销商获得或调出商品的调整价格,假定PkB≥PkS;γk是经销商k的补偿支付,如果γk>0,则意味着经销商需要支付一笔费用出来参与调整库存; 相反若γk < 0,则他通过参与这个协议可以收到一笔补偿金|γk|。比起单纯的批发协议,经销商利用这个其他经销商参与的库存调整协议可使其获利更多或减少损失。当然,实际中协议约定的价格,以及wk、PkB和PkS等可能是某个数值,也可能是某个函数,跟第2期间的库存状况等具有相关性。设定一个Stackelberg模型,供应商作为引导者,如果他提供的协议可以提升整个系统的利润水平,他将采用充分协调及提供补偿支付的方式推行这个协议,让经销商都能参与,当然供应商也能最终通过系统增加的利润获得补偿。当经销商参与进来,他们之间也形成一个纳什均衡的博弈:如果合同价格是常数,这个博弈只影响独立决策的个别经销商(根据价格自行决定其批发数量增加或减少);如果合同规定价格不是常量的,而是跟库存水平等相关,这个博弈可能就不完全。因此,这里假设供应链中各方之间的信息对称。
对于经销商k,yk是第1期间的采购数量,zkB和zkS分别代表经销商在第2期间增加或减少的库存比重,在第2期间,经销商最大利润期望为Π2kr(xk|x-k),其中xk表示该经销商此时的库存水平,而x-k表示其他经销商的库存水平,x-k=[x1, …, xk-1, xk+1, …, xn]。
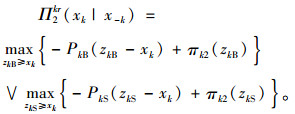
|
(7) |
yk表示该经销商的批发数量,而y-k表示其他经销商的批发数量,第1期间该经销商最大利润期望函数为
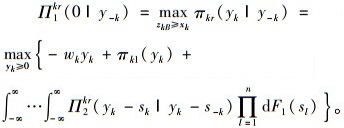
|
(8) |
对于第2期间,经销商需要补充不够的库存或减少多余的库存,因此其调节合同的价格PkB和PkS,其数值存在最优增加买入价格和卖出减少价格分别为
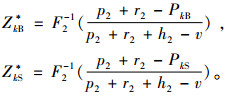
|
最后,经销商第1期间的最优采购数量,其纳什均衡可以通过方程πkr'(yk|y-k)=0, k=1, …, n进行求解。
对于供应商,在给定了经销商的最优条件之后,经销商需要确定每一个期间的最佳生产量,其中第1期间最优的生产量为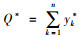
第2期间是否增加生产决定于商品转运之后是否满足了加货需求,若要增加生产,产量为二者之间差值。
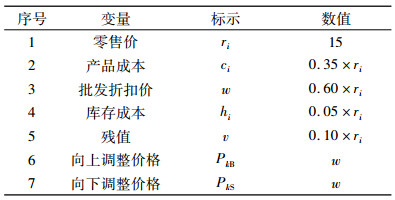
3 验证案例 3.1 案例基本假设本研究案例的选择需满足3个条件:1)存在一个供应商和多家经销商的供应链系统;2)经销商之间不发生横向集中转运;3)存在通过供应商引导的转运库存调节行为。经过调研及筛选,发现国内一家漫画出版与发行公司——广州漫友文化科技发展有限公司供应链基本符合这些特征。该公司为漫画书刊的供应商,每月都向经销商批发很多动漫读物,在全国有5个一级经销商(分别在广州、武汉、北京、上海及成都)及若干中小经销商,公司与这些经销商签订了供货协议,但各经销商之间并没有签约或存在联盟关系。该公司安排部分经销商之间在每月销售末期按约定条件进行转运调货,相关货物转运信息和款项往来通过供应商和经销商之间纵向完成,符合纵向集中而横向分散的半分散型供应链系统特点。
漫友产品供应链各参数指标如表 1,该公司采用了恒定批发价方式调整库存。本研究将使用双周期模型对3种供应链状态(集中型、半分散型及完全分散型)的数据进行对比,看哪种类型优化效果更好。其中,半分散型模式为企业实际发生数据,而集中型、完全分散型为推导和运算数据。
| 表 1 验证模型的基本指标 Tab. 1 Base parameters for the computational study about the case |
根据双周期模型的3种情况。1)在集中型供应链中,供应商和经销商之间的最优决策是联合决定的,当然决策者是供应商,所有经销商参与调节,在第1个期间和第2个期间的开始阶段都进行生产。在第1期间供应商需要决定最优生产量及如何最优地将所需库存分配给各个经销商;在第2期间开始,供应商也通过第1期间的销售情况,在经过所有经销商参与(横向及纵向)调节后决定最优生产量及每个经销商的重新分配理想数量。2)在完全分散型模式下,经销商在经历第1期间的销售后,只能通过与供应商进行直接沟通,库存过多则退回货物接受处罚,若货物不够则进行直接补货。3)本案例实际情况为半分散型供应链(纵向集中而横向分散),供应商与各经销商签订了调节库存协议,目的是改进经销商及整个供应链增加企业利润。依照此合同,在第2期间初始,每个经销商可以根据自己在第1期间的销售量及与供应商早在生产启动之前商定加货或退货的价格调整自己的库存量。当然,这里的“购买”和“卖出”都是虚拟的,实际的库存是通过供应商的牵线直接由货多的经销商A运给了缺货的经销商B。所以这个双向可调节合同是实现供应商引导调节,并使经销商可以进行独立决策的关键工具。
优化效果跟提前约定的处罚成本数值相关,通常有3种情况:P1表示经销商在2个期间对未销售出商品的处罚相同;P2表示对第1期间的处罚重于第2期间;P3表示第2期间的处罚重于第1期间。对经销商的处罚成本类别见表 2。
| 表 2 对经销商的处罚成本类别 Tab. 2 Category of penalty cost to the retailers |
除了处罚成本,模型的优化效果还与经销商在两个期间的采购量比重相关。假定经销商采购需求呈正态分布,D1表示第1、第2期间采购数量均值与标准差都相同;D2、D3表示在第2期间的采购量均值和标准差比第1期间要小,在后两种情况下,在第1期间结束的时候经销商更有动力调节多余的商品给其他经销商,调节效应更大。经销商的需求分布参数见表 3。
| 表 3 经销商的需求分布参数 Tab. 3 Parameters of the demand distributions for retailers |
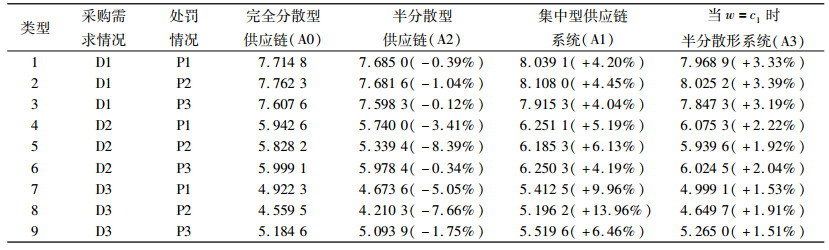
本研究以完全分散型供应链(A0)作为基准,与集中型(A1)和半分散型(A2)的供应链优化数值做比较,看哪种方式的优化效果较好。同时调整参数,得到A3的数值(表 4)。
| 表 4 集中型、半分散型、完全分散型供应链的优化效益比较(百万元人民币) Tab. 4 Comparison of centralized, semi-decentralized and decentralized systems(RMB1000, 000) |
从表 4可看出,整体而言,集中型供应链系统的(A1)优化效果最佳;其次是完全分散型供应链系统(A0);优化效果最差的是半分散型供应链(A2)。这一结果似乎与预期的结果并不一致,但当改变条件使“w=c1”的情况下(A3),半分散型供应链优化效果明显增加。
4 结论及未来研究方向通过文献分析发现,双周期条件下纵向集中而横向分散的半分散型供应链均衡问题是一个重要课题,因此本研究利用数学方法建立了一个双周期可变协议供应链模型,分别从集中型和半分散型两种情形进行推导,求解出最优均衡决策,最后进行实证检验,研究形成了3个方面的基本结论。
4.1 存在双周期集中式供应链的数量均衡条件供应商存在第1期间的最优产量Y0,以及第2期间的最优产量ZQ0:当库存量x < ZQ0,供应商增加产量水平到ZQ0并分发给各经销商,使其库存水平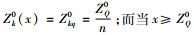
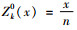
供应商通过协议方式确定与各经销商之间的博弈关系:供应商(主)和经销商(从)之间为主从博弈,经销商之间为纳什博弈,协议允许经销商根据协议价格及自身情况调整库存量,且可以独立决定是否接受供应商提供的协议:若拒绝,可从经销商处进行补货或退回货物;而选择接受协议的经销商需在纳什博弈中决定自己的第1期间的批发量和第2周期采购量,达到可能存在的纳什均衡:经销商第1期间最优采购量可通过π'kr(yk|y-k)=0, k=1, …, n进行求解,此时供应商最优的生产量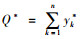
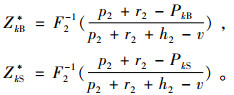
|
通过漫友公司的实际案例验证结果发现,在双周期模型中,优化效果最好是集中式供应链(最高13%),但其在现实中操作难度较大;半分散式与完全分散式供应链系统进行比较,发现其优化效果与供应商制定的批发价和实际生产成本之间的数值接近程度相关:当批发价接近成本时,优化效应最为显著(最高3.39%);反之,若批发价与成本偏离过大,则半分散式供应链产生的效益甚至比完全分散式更差(最多降8.39%)。因此,可变调节协议的指标设定尤为重要。此外,可调节协议设定的处罚条款(P)及经销商在两期间的需求分布(D)对3种供应链的优化效果均存在调节效应。
当然,本研究存在一定局限性:1)研究中忽略了运输成本; 2)对供应链个体之间信息对称性、消费需求的分布更新等影响要素未展开分析。此外,只验证了漫友文化一家公司的实际数据,若能纳入更多企业的数据进行验证,更能确保模型的可靠性。这些将在以后的研究中不断完善和探索。
| [1] |
SINGHA, PARTHANADEE, BUDDHAKULSOMSIRI.A comparison of inventory management between decentralized and centralized distribution networks with backorder//Industrial engineering management science and applications 2015[M].Berlin:Springer Berlin Heidelberg, 2015, 349(1):485-490.
|
| [2] |
HAO H., KRISHNAN H., MCCORMICK S T.. Incentives for transshipment in a supply chain with decentralized retailers[J].
Manufacturing & Service Operations Management, 2011, 13(3): 361-372.
|
| [3] |
LI R, RYAN J K. Inventory flexibility through adjustment contracts[J].
International Journal of Production Research, 2012, 50(7): 1955-1978.
DOI: 10.1080/00207543.2011.564667. |
| [4] |
AGRAWAL V, CHAO X, SESHADRI S. Dynamic balancing of inventory in supply chains[J].
European Journal of Operational Research, 2004, 159(2): 296-317.
DOI: 10.1016/j.ejor.2003.08.017. |
| [5] |
李晓宏, 孙林岩, 李刚. 需求信息更新条件下经销商间调货策略研究[J].
系统工程学报, 2008, 23(6): 689-695.
LI X H, SUN L Y, LI G. Research on horizontal transshipment policy with demand information updating[J]. Journal of Systems & Engineering, 2008, 23(6): 689-695. |
| [6] |
李怡娜, 徐学军. 双分销渠道下短生命周期产品供应链转运策略[J].
计算机集成制造系统, 2010, 16(1): 155-164.
LI Y N, XU X J. Supply chain transshipment strategy for short life-cycle product under dual-channel[J]. Computer Integrated Manufacturing Systems, 2010, 16(1): 155-164. |
| [7] |
ANUPINDI R, BASSOK Y, ZEMEL E. A general framework for the study of decentralized distribution systems[J].
Manufacturing & Service Operations Management, 2001, 4(3): 349-368.
|
| [8] |
KLEINDORFER P R, WU D J. Integrating long-and short-term contracting via business-to-business exchanges for capital-intensive industries[J].
Management Science, 2003, 49(11): 1597-1615.
DOI: 10.1287/mnsc.49.11.1597.20583. |
| [9] |
MOINZADEH K, NAHMIAS S. A continuous review model for an inventory system with two supply modes[J].
Management Science, 1988, 34(6): 761-773.
DOI: 10.1287/mnsc.34.6.761. |
| [10] |
MOINZADEH K, NAHMIAS S. Adjustment strategies for a fixed delivery contract[J].
Operations Research, 2000, 48(3): 408-423.
DOI: 10.1287/opre.48.3.408.12435. |
| [11] |
RUDI N, KAPUR S, PYKE D F. A two-location inventory model with transshipment and local decision making[J].
Management Science, 2001, 47(12): 1668-1680.
DOI: 10.1287/mnsc.47.12.1668.10235. |
| [12] |
HU X, DUENYAS I, KAPUSCINSKI R. Existence of coordinating transshipment prices in a two-location inventory model[J].
Management Science, 2007, 53(8): 1289-1302.
DOI: 10.1287/mnsc.1060.0694. |
| [13] |
钱宇, 陈剑. 供应链中考虑下游转运的订货和定价决策研究[J].
中国管理科学, 2008, 12(1): 53-60.
QIAN Y, CHEN J. Research on ordering and pricing decisions in a supply chain with downstream transshipment[J]. Chinese Journal of Management Science, 2008, 12(1): 53-60. |
| [14] |
GRANOT D, SOSIC G A. Three-stage model for a decentralized distribution system of retailers[J].
Operations Research, 2003, 51(5): 0771-0784.
DOI: 10.1287/opre.51.5.771.16749. |
| [15] |
HUANG X, SOSIC G. Transshipment of inventories: dual allocations vs. transshipment prices[J].
Manufacturing & Service Operations Management, 2010, 12(2): 299-318.
|
| [16] |
YAN X, ZHAO H. Inventory sharing and coordination among n independent retailers[J].
European Journal of Operational Research, 2015, 243(2): 576-587.
DOI: 10.1016/j.ejor.2014.12.033. |
| [17] |
HANANY E, TZUR M, LEVRAN A. The transshipment fund mechanism: coordinating the decentralized multilocation transshipment problem[J].
Naval Research Logistics, 2010, 57(4): 342-353.
|
| [18] |
陈敬贤, 王国华, 梁樑. 协调多经销商横向转载的收益共享契约[J].
中国管理科学, 2013, 21(3): 80-87.
CHEN J X, WANG G H, LIANG L. The revenue-sharing mechanism: coordinating the multiloeation lateral transshipment problem[J]. Chinese Journal of Management Science, 2013, 21(3): 80-87. |
| [19] |
禹爱民, 刘丽文. 供应链下游经销商的转运库存策略[J].
系统管理学报, 2013, 22(1): 1-9.
YU A M, LIU L W. The transshipment between two types of retailers in the downstream supply chain[J]. Journal of Systems & Engineering, 2013, 22(1): 1-9. |
| [20] |
DONG L, RUDI N. Who benefits from transshipment? Exogenous vs. endogenous wholesale prices[J].
Management Science, 2004, 50(5): 654-657.
|
| [21] |
RONG Y, SNYDER L V, SUN Y. Inventory sharing under decentralized preventive transshipments[J].
Naval Research Logistics, 2010, 57(6): 540-562.
DOI: 10.1002/nav.v57:6. |
| [22] |
SHARMA, ABOUEE, BERMAN. Optimal joint replenishment and transshipment policies in a multi-period inventory system with lost sales[J].
Operations Research, 2015, 63(2): 342-350.
DOI: 10.1287/opre.2015.1358. |
 2016, Vol. 19
2016, Vol. 19