平稳的电力供给是维持社会正常生产生活的保证,而电力物资是确保电力供应安全、生产运行稳定和故障修复及时的基础。然而,大部分电力物资呈间断需求,这种需求特性使得对电力物资的库存管理陷入两难困境。一方面,如果精简库存,则无法保证电力物资的及时供应,影响电网的高效运行和企业现金流的正常运转;另一方面,如果提高库存水平,则会产生高额的库存成本和报废损失。因此,如何提升间断需求电力物资的库存管理水平,是电网企业面临的重大挑战之一。
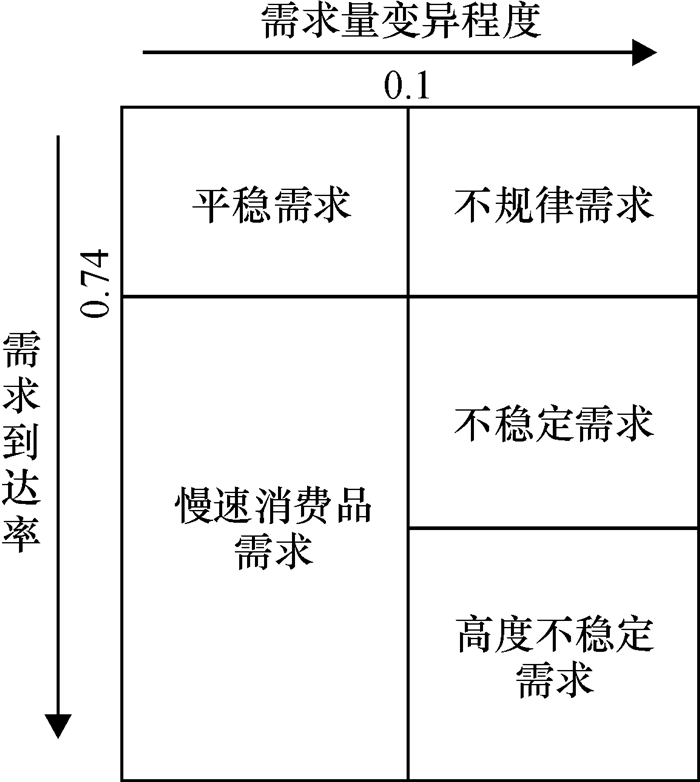
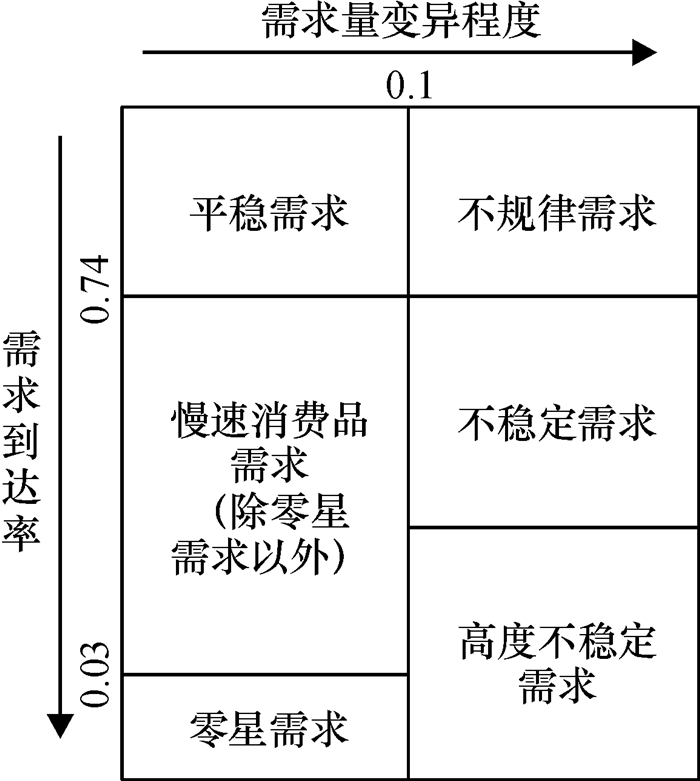
以往的ABC分类法[1]在快销业以及传统的制造业里面应用非常广,但对于电力物资来说,由于其主要应用在运行维护以及建设项目方面,其中建设项目中的物资属于A类,SKU数目不多,需求量占比几乎高达80%,这些物资一般是连续需求或者是单次批量很大的间断需求,其需求预测方法以及库存控制策略均比较成熟;而用于运行维护的物资集中在B类及C类,SKU数目非常多,其需求量占比不大,且绝大多数物资的需求呈间断特征,所以有必要更加深入地对属于B、C类的间断需求电力物资进行分类和分析。Eaves[2]根据需求量变异程度和需求到达率将需求分为五类, 如图 1所示,其中,“慢速消费品需求”、“不稳定需求”和“高度不稳定”三类属于间断需求。本文的研究对象零星需求就是电力物资间断需求里面最难的一类,属于C类物资。这类零星需求每年只发生几次,或者很多年才发生一次,是电力物资需求预测的重难点,所以本文对Eaves的分类重新进行了刻画,即以需求到达率0.03为临界值,将“慢速消费品需求”分成两部分,其中需求发生频率较低(即需求到达率小于0.03)的部分为零星需求,如图 2所示。众所周知,对不同种类的物资应该采取不同的库存控制策略。有的电力物资可以采用备库等方式,而呈零星需求特性的电力物资一般采取协议采购的策略,即由电力公司预测出未来一段时间内零星需求物资的采购金额,并将相关预测信息共享给距离电力公司较近的供应商,向供应商确保在这段时间内消耗库存。这样一来,电力公司本身无需设置安全库存,同时,供应商根据协议进行备货,可以大大降低其库存成本。
|
图 1 Eaves提出的需求分类 Fig. 1 Eaves' categorization scheme |
|
图 2 本文的需求分类 Fig. 2 Our categorization scheme |
以往研究中对间断需求产品库存管理的方法大致可以分为两类。一类方法将间断需求序列拟合成复合分布,以成本为导向建模,得到最低期望成本下的库存水平作为最优库存水平。文献[3-13]分别研究了复合伯努利分布、复合泊松分布和复合伊朗分布下的最优库存策略。这些模型得出的间断需求产品最优库存水平相较于传统的报童模型都有一定优越性,但是对于需求序列难以拟合成复合分布的零星需求,这种方法是无效的。另一类方法通过预测产品需求得到最优库存水平。为了解决间断需求预测问题,以往的文献中提出了多种方法。其中许多方法都来源于对军事备件使用率的预测[14]。Haber等[14]考察了几种间断需求产品的预测方法,其中包括基于专家意见归类预测的方法。Silver[15]以及Smith等[16]提出了基于历史数据预测间断需求的贝叶斯方法。Syntetos等[17]提出了对Croston[18]步骤纠偏的SBA方法。Levén等[19]提出了基于Croston[18]方法的ERP系统执行方案,既可以预测快消品需求,也可以预测间断需求;然而,这个方法是有偏的[20]。Willemain等[21]将马尔科夫链与Bootstrap方法结合来预测间断需求。Altay等[22]对Wright[23]提出的Holt方法进行修正,并将其与Croston[18]方法比较。许绍杰等[24]提出一种针对间断需求的组合预测模型,该模型从自相关序列和解释变量序列两个方面进行组合预测,并对两个预测结果进行整合得到最终的预测结果。王文[25]提出了基于时间序列的支持向量机预测和基于影响因素的支持向量机的间断需求预测方法,并通过实例研究验证了这两种方法的有效性。这些需求预测方法都从不同角度预测了特定类型的间断需求,但是在预测发生次数极少、量极小的零星需求时效果并不好。因此,这两类解决间断需求库存管理的方法均不适用于零星需求。
针对零星需求的特点,Dalhart[26]提出了产品池的概念,即将多种产品归集起来预测总体需求。这种思路有效地规避了零星需求数据量少的研究困境。在此基础上,Dekker等[27]将产品按照季节性类型分成不同的产品池,对每个产品池以季节性指数为依据预测未来需求,得到远高于Holt-Winter模型的预测精度。Caniato等[28]的研究表明,基于产品池的预测方法更加适应季节性变动或管理性变动的产品需求,而对于随机变动的产品需求效果不好。Shenstone等[29]对4种预测模型得到的产品池未来需求作出区间估计,作为合理的库存水平。这种区间估计的方法虽然避免了单纯使用需求率作为库存管理依据而带来的误导,但是需要通过预测模型模拟生成大量需求估计值,而这些预测模型并不适用于零星需求。针对这些研究的缺陷,Lindsey等[30]以产品池为研究对象,提出了一种对产品池内未发生历史需求产品的总需求率作区间估计的方法。
本文基于Lindsey等[30]提出的方法,将一个零星需求产品组内发生1个和2个需求的产品数目作为区间估计输入值,对产品组内未发生需求的产品集合建立未来总需求率的区间估计。选取3个参数:产品组规模、单个产品理论需求率和置信水平,对区间估计进行可靠性检验,得到此方法适用的参数范围,然后选择符合参数条件的电力物资构建产品组。产品组内所有电力物资在数据期间内均发生需求,但是从中截取一个连续的时间片段,则会有一些物资在这段时间内呈零需求,这些物资组成目标产品集合。对目标产品集合作总体理论需求率的区间估计。根据目标产品集合在整个时间长度内的实际需求率,对它们的单价加权平均,得到这些物资的总体单价水平。将这个单价水平与区间估计结果相乘,计算出这些物资单位时间内供应所需资金,以此作为相应物资协议采购合同的金额。通过协议采购,采购方与供应商能达成良好的合作关系,提高采购效率,也保证了物资的及时供应,顺应国网公司集约化物资管理的趋势,有效地解决了零星需求电力物资的采购和库存管理难题。
1 方法介绍本文的研究对象是一个零星需求产品组,假设产品组内所有产品需求独立且服从泊松分布。在观察期间内,产品组内未发生需求的产品构成了目标产品集合。这个目标产品集合的总体理论需求率及其区间估计是本方法最终要求的结果。以下是运算中需要用到的变量和符号:
n为产品组内产品数目;
λi为产品i的理论需求率,i=1, 2, …n;
t为需求观察期时长;
ψi(t)表示若i在t期间内未发生需求则为1,若发生需求则为0;
Mj(t)表示在t期间,发生了j次需求的产品数目;
M1(t)/t为∧(t)的统计量;
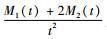
Zα/2为标准正态概率分布上侧面积为α/2时的Z值。
∧(t)是未发生需求产品的理论需求率之和,即目标产品集合的总体理论需求率。根据定义,
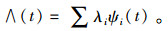
|
(1) |
因为假设产品组内所有产品的需求均服从泊松分布,所以由泊松分布期望公式,可以得到
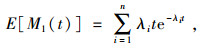
|
(2) |
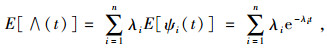
|
(3) |
即
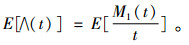
|
(4) |
同理可得
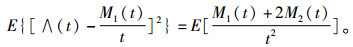
|
(5) |
由上可知,M1(t)/t是∧(t)的无偏估计量,而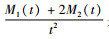
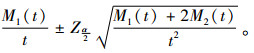
|
(6) |
其中α为标准第1类错误率,取1%、5%或10%,分别对应99%、95%和90%的置信水平。
显然,区间估计可靠性受M1(t)/t分布的拟合优度影响,而拟合优度与一系列参数取值相关。本文选用3个参数:产品组规模、单个产品理论需求率和置信水平,通过两个模拟实验,探究在怎样的参数范围内,区间估计的结果是可靠的,为之后在实际物资中选取产品组和目标产品集合提供依据。
根据这种方法,仅通过观察期间零星需求产品组内发生1个和2个需求的产品数目以及时间长度,就可以得到产品组内未发生需求产品组成的目标产品集合的总体理论需求率的区间估计。根据目标产品集合的总体需求率和价格水平,可以确定协议采购中的合同金额。
2 数值分析 2.1 可靠性检验因为无法精准把握实际物资的理论需求率,所以不使用实际电力物资进行可靠性检验,而使用模拟生成的需求序列。本文的数据中包含2 330种电力物资在157周的需求信息,且所有物资在数据期间均发生至少1个需求,则从中截取时间长度为100周的数据,会显示有部分物资呈零需求。因此,本文选择100周作为模拟使用的时间长度,在后文对电力物资进行需求率区间估计时也将截取100周数据。
为了确定可靠区间估计下产品组规模的范围,进行模拟1。为保证产品组中有足量的产品在100周内发生0、1或2个需求,设定1/100、1/200和1/300三种单个产品理论需求率取值。同时,为覆盖所有电力物资数据,设定产品组规模范围在50个到2 500个之间。模拟1具体参数选取如下:
产品组规模/个:50,100,150,200,250,300,350,400,450,500,600,700,800,900,1000,1500,2000,2500;
单个产品理论需求率(个/周):1/300,1/200,1/100;
置信水平:90%,95%,99%。
将这些参数相互组合,得到18×3×3=162种参数组合。本文将在这162种参数设置下分别进行模拟实验,探究在怎样的产品组规模条件下能够得到可靠的区间估计。
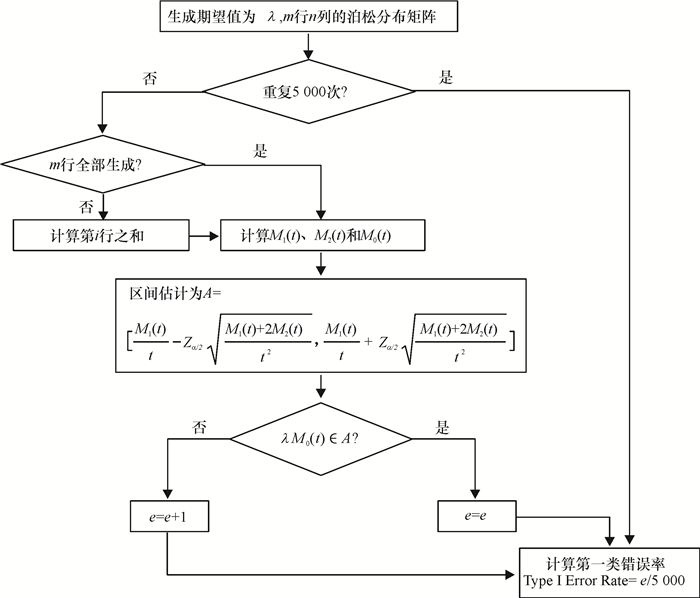
以产品组规模为200个,单个产品理论需求率为1/300(个/周),置信水平为95%的参数组合为例来说明模拟实验的过程。操作流程如图 3。
|
图 3 模拟实验流程图 Fig. 3 The flow chart of simulation experiment |
1) 生成期望为1/300、200行、100列的泊松分布矩阵,以此模拟包含200个产品的产品组(所有产品需求率均为1/300)在100个时间长度下的需求数据,矩阵中的每一行都代表其中一个产品的需求数据。
2) 计算每一行之和,并计算和为1和2的个数,分别得到M1(t)和M2(t),在t=100和置信水平为95%的设定之下由公式计算出估计区间。
3) 计算和为0的个数,得到M0(t),将其乘以泊松分布的期望即1/300,得到未发生需求产品理论需求率之和。若此结果在第2步估计出的区间之内,则不发生第1类错误;若不在区间之内,则发生第1类错误。
4) 上述步骤重复5 000次,计算出第1类错误发生的次数和错误率。若第1类错误率在可接收范围之内,则认为区间估计结果可靠;反之,则认为区间估计结果不可靠。设定α前后两个标准差之内为可接受范围。则α为1%、5%和10%时对应的可接受范围分别是[0.007,0.013]、[0.044,0.056]和[0.092,0.108]。
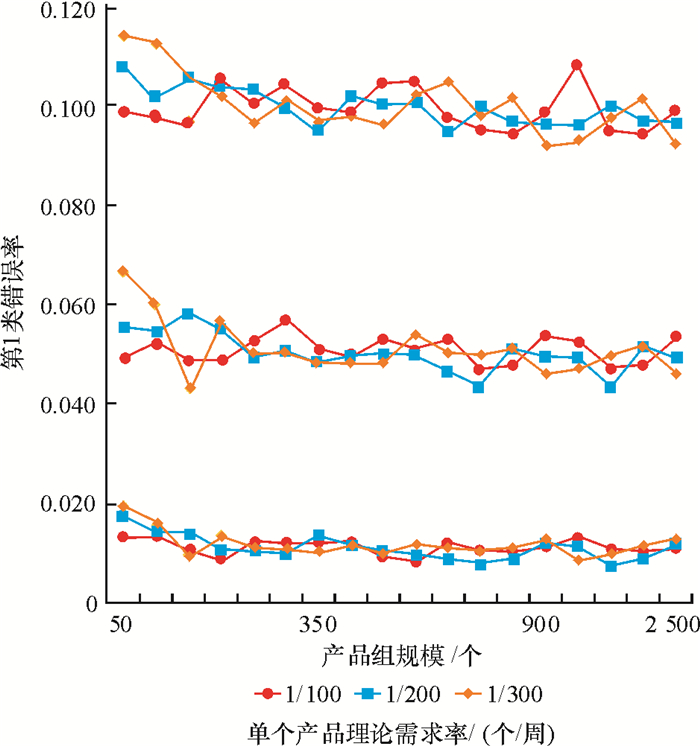
对162种参数组合下区间估计可靠性的检验结果见表 1和图 4。由图 4可知,当产品组规模过小或过大时,得到的区间估计结果不可靠;当产品组规模在350~900之间时,对产品组内未发生需求产品理论需求率之和的区间估计较为可靠。在对电力物资构建产品组时,产品组规模选取要在350~900之间。
|
图 4 模拟1第1类错误率 Fig. 4 Type Ⅰ error of simulation 1 |
| 表 1 模拟1第1类错误率 Tab. 1 Type Ⅰ error of simulation 1 |
为了确定可靠区间估计下单个产品理论需求率的范围,进行模拟2。为使结果不因产品组规模的取值而产生偏差,模拟2中产品组规模取值不变。根据模拟1,产品组规模在350~900之间时,区间估计结果较为可靠。为了简化模拟过程,选择这个范围的最小值350作为模拟2中的产品组规模。2 330种电力物资在157周的实际需求率在1/157到1(个/周)之间。由于时间序列长度只有157,实际需求率可能略高于理论需求率,所以在设定需求率时,也选取了一些小于1/157(个/周)的值。本文对模拟2的参数选取如下:
产品组规模/个:350;
单个产品理论需求率(个/周):1/1 000,1/800,1/600,1/400,1/300,1/200,1/100,1/50,1/30,1/20,1/15,1;
置信水平:90%,95%,99%。
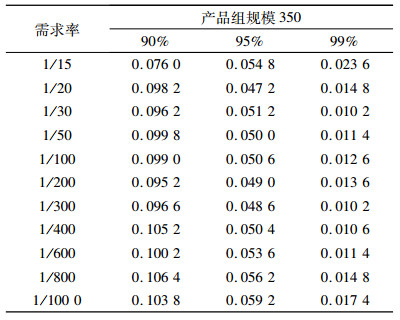
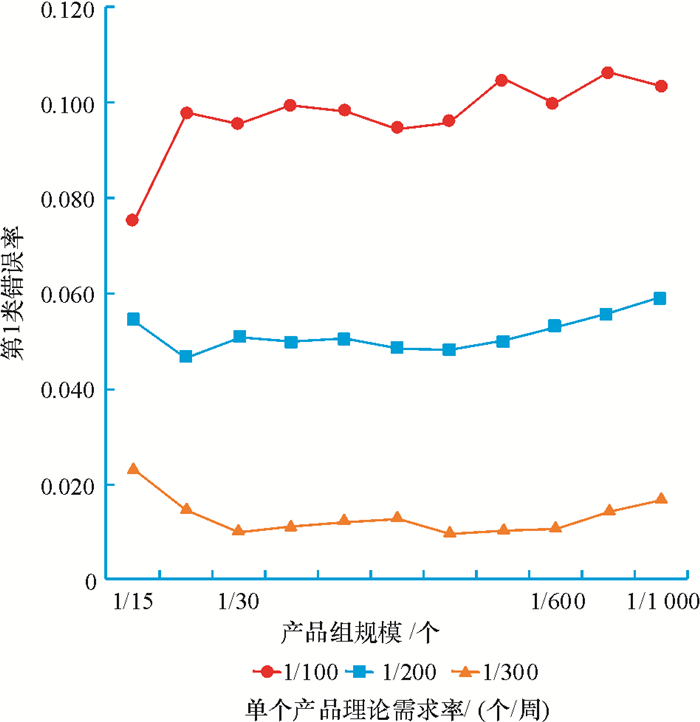
因此得到12×3=36个参数组合。与模拟1的步骤相同,模拟2在36种参数组合下,探究得到可靠区间估计下的单个产品理论需求率范围。模拟结果见表 2和图 5。由于当单个产品理论需求率为1(个/周)时,在100周内,所有产品发生需求均超过2个,也即发生0或1个需求的产品数目均为0,区间估计结果没有实际意义,所以模拟结果中不包含这种情况。
|
图 5 模拟2第1类错误率 Fig. 5 Type Ⅰ error of simulation 2 |
| 表 2 模拟2第1类错误率 Tab. 2 Type Ⅰ error of simulation 2 |
从图 5可以看出,当单个产品理论需求率在1/600~1/30之间时,区间估计可靠性较高。
2.2 零星需求电力物资需求率区间估计首先,选取产品组。由于当单个产品理论需求率为1/600~1/30时,区间估计准确性较高,所以筛选出实际需求率在这个区间中的物资。对这些筛选出的物资进行泊松分布拟合检验,得到需求服从泊松分布的物资,一共631种。631在350~900之间,所以就选取这631种物资作为产品组。
然后,定位目标产品集合。本文截取了第58周到第157周的数据,发现在这631种物资中,有137种物资在这100周中未发生需求。因此,本文就将这137种物资定位为目标产品集合。
最后,根据产品组在所选100周时间长度内的需求数据,由式(6)得到目标产品集合的总体理论需求率及其区间估计。在置信水平为90%、95%和99%时,区间估计结果分别为[1.40,2.16]、[1.33,2.23]和[1.19,2.37](个/周)。计算这137种产品在整个157周的实际需求率之和,结果为1.57(个/周),落在上述3个区间之内。由此可以判定,对这137种物资总需求率的区间估计在3个置信水平下都是可靠的。
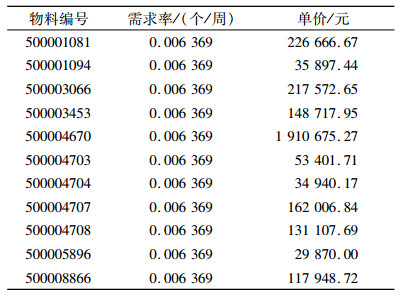
2.3 协议采购方案拟定表 3为部分目标集合内物资的实际需求率及单价。本文将目标产品集合在157周内的实际需求率作为权重,对它们的单价加权平均,得到这个目标产品集合的总体单价水平为人民币30 190.16元。则在90%、95%和99%3种置信水平下,这些物资所需的金额区间估计分别为[42 326.84,65 150.13]、[40 141.63,67 335.34]和[35 875.27,71 601.70](元/周)。采购方可根据不同考量,由上述区间中选取合适的金额作为协议采购合同金额。
| 表 3 目标产品集合需求率与单价示例 Tab. 3 The demand rate and the unit price of the target product set> |
上述对于这137种物资的协议采购方案只是一个例子。在现实的电力物资采购中,各种物资来源于不同的供应商。因此,可以将电力物资需求数据按照供应商不同分开,对每一个供应商所供应的物资按照以上方法计算协议采购合同金额。
在协议采购方案的构建中,本文从所有数据中截取一个100周的时间长度,最后得到对这个时间长度内未发生需求的物资理论需求率之和的区间估计,但是对那些在这个期间中发生过少量需求(例如需求量为1个)的物资,并没有估计出需求水平。针对这个问题,可以截取不同的时间片段,作多次需求水平的区间估计,但是这种处理方法在实际中有诸多不便,所以需要改进优化,使其操作更加简易。
3 结论无论是通过需求拟合复合分布,还是通过需求预测,对间断需求物资尤其是零星需求物资作库存管理是很困难的,这也成为企业管理者面对的重大挑战之一。本文提出的方案对这些电力物资实行零库存,通过框架采购协议,实现物资随时需求随时供给,达到100%的服务水平,同时实现了零库存成本和零短缺成本的库存管理目标,且不会因为突然的需求而消耗大量现金流。本文提出的区间估计方法能够很好地适应零星需求电力物资特性,对框架协议的构建特别是合同金额的确定有指导作用。
但是这种方法仍然存在一些局限性。1)本文的方法只有在产品需求服从泊松分布时才能成立,这就使得这种方法对一部分物资是不适用的。2)在检验Lindsey等[30]提出的区间估计的方法可靠性时,设定每一个产品组所有产品的理论需求率相同,这一设置在实际中并不适用。在从区间估计角度对零星需求物资作库存控制和协议采购的未来研究中,可以探究其他需求分布下的区间估计方法。
| [1] |
郑美凤. 有限需求信息下的间断需求预测及库存控制研究[D]. 上海: 上海大学, 2012.
ZHENG Meifeng. Intermittent demand forecast and inventory control in the presence of limited historical demand data [D]. Shanghai: Shanghai University, 2012. |
| [2] |
EAVES A H C, KINGSMAN B G. Forecasting for the ordering and stockholding of consumable spare parts[J].
Journal of the Operational Research Society, 2004, 55(4): 431-437.
DOI: 10.1057/palgrave.jors.2601697. |
| [3] |
FEENEY G J, SHERBROOKE C C. The (S-1, S) inventory policy under compound Poisson demand[J].
Management Science, 1966, 12(5): 391-411.
DOI: 10.1287/mnsc.12.5.391. |
| [4] |
MATHEUS P, GELDERS L. The (R, Q) policy subject to a compound Poisson demand pattern[J].
International Journal of Production Economics, 2000, 68(3): 307-317.
DOI: 10.1016/S0925-5273(99)00110-3. |
| [5] |
BABAI M Z, DALLERY J Z Y. Analysis of order-up-to-level inventory systems with compound Poisson demand[J].
European Journal of Operational Research, 2011, 210(3): 552-558.
DOI: 10.1016/j.ejor.2010.10.004. |
| [6] |
DUNSMUIR W T M, SNYDER R N. Control of inventories with intermittent demand[J].
European Journal of Operational Research, 1989, 40(1): 16-21.
DOI: 10.1016/0377-2217(89)90267-1. |
| [7] |
JANSSEN F, HEUTS R, DE KOK A. On the (R, s, Q) inventory model when demand is modelled as a compound Bernoulli process[J].
European Journal of Operational Research, 1998, 104(3): 423-436.
DOI: 10.1016/S0377-2217(97)00009-X. |
| [8] |
TEUNTER R H, SYNTETOS A A, BABAI M Z. Determining order-up-to levels under periodic review for compound binomial(intermittend) demand[J].
European Journal of Operational Research, 2010, 203(3): 619-624.
DOI: 10.1016/j.ejor.2009.09.013. |
| [9] |
LARSEN C, THORSTENSON A. A comparison between the order and the volume fill rates for a base-stock inventory control system under a compound renewal demand process[J].
Journal of the Operational Research Society, 2008, 59(6): 798-804.
DOI: 10.1057/palgrave.jors.2602407. |
| [10] |
GUPTA A K, ZENG W B, WU Y. Probability and statistical models:foundations for problems in reliability and financial mathematics[M]. Boston: Springer Science + Business Media, LLC, 2010.
|
| [11] |
LARSEN C, THORSTENSON A. The order and volume fill rates in inventory control systems[J].
International Journal of Production Economics, 2014, 147: 13-19.
DOI: 10.1016/j.ijpe.2012.07.021. |
| [12] |
LARSEN C, KIESMULLER G P. Developing a closed-form cost expression for an (R, s, nQ) policy where the demand process is compound generalized Erlang[J].
Operations Research Letters, 2007, 35(5): 567-572.
DOI: 10.1016/j.orl.2006.11.002. |
| [13] |
SAIDANE S, BABAI M Z, AGUIR M S, et al. On the performance of the base-stock inventory system under a compound Erlang demand distribution[J].
Computers & Industrial Engineering, 2013, 66(3): 548-554.
|
| [14] |
HABER S E, SITGREAVES R. A methodology for estimating expected usage of repair parts with application to parts with no usage history[J].
Naval Research Logistics Quarterly, 1970, 17(4): 535-546.
DOI: 10.1002/(ISSN)1931-9193. |
| [15] |
SILVER E A. Bayesian determination of the reorder point of a slow moving item[J].
Operations Research, 1965, 13(6): 989-997.
DOI: 10.1287/opre.13.6.989. |
| [16] |
SMITH B R, VEMUGANTI R R. A learning model for inventory control of slow-moving items[J].
AIIE Transactions, 1969, 1(3): 274-277.
DOI: 10.1080/05695556908974443. |
| [17] |
SYNTETOS A A, BOYLAN J E. On the Bias of intermittent demand estimates[J].
International Journal of Production Economics, 2001, 71(1): 457-466.
|
| [18] |
CROSTON J D. Forecasting and stock control for intermittent demands[J].
Journal of the Operational Research Society, 1972, 23(3): 289-303.
DOI: 10.1057/jors.1972.50. |
| [19] |
LEVÉN E, SEGERSTEDT A. Inventory control with a modified Croston procedure and Erlang distribution[J].
International Journal of Production Economics, 2004, 90(3): 361-367.
DOI: 10.1016/S0925-5273(03)00053-7. |
| [20] |
BOYLAN J, SYNTETOS A. The accuracy of a modified Croston procedure[J].
International Journal of Production Economics, 2007, 107(2): 511-517.
DOI: 10.1016/j.ijpe.2006.10.005. |
| [21] |
WILLEMAIN T R, SMART C N, SCHWARZ H F. A new approach to forecasting intermittent demand for service parts inventories[J].
International Journal of Forecasting, 2004, 20(3): 375-387.
DOI: 10.1016/S0169-2070(03)00013-X. |
| [22] |
ALTAY N, RUDISILL F, LITTERAL L A. Adapting Wright′s modification of Holt′s method to forecasting intermittent demand[J].
International Journal of Production Economics, 2008, 111(2): 389-408.
DOI: 10.1016/j.ijpe.2007.01.009. |
| [23] |
WRIGHT D J. Forecasting data published at irregular time intervals using an extension of Holt′s method[J].
Management Science, 1986, 32(4): 499-510.
DOI: 10.1287/mnsc.32.4.499. |
| [24] |
许绍杰, 张衡, 聂涛, 等. 基于组合预测的间断性需求器材预测[J].
系统工程与电子技术, 2012, 34(1): 111-114.
XU Shaojie, ZHANG Heng, NIE Tao, et al. Forecasting for materials with intermittent demand based on combined forecasting[J]. Systems Engineering and Electronics, 2012, 34(1): 111-114. |
| [25] |
王文. 基于支持向量机的不常用备件需求预测方法研究[D]. 武汉: 华中科技大学, 2006.
WANG Wen. Research on support vector machines based forecasting method for rarely used spare parts demand. [D]. Wuhan: Huazhong University of Science and Technology, 2006. |
| [26] |
DALHART G. Class seasonality-a new approach [C]. Proceedings of 1974 Conference of American Production and Inventory Control Society, October 21-25, 1974, 2nd edn. APICS, Washington, DC, 1974: 11-16.
|
| [27] |
DEKKER M, VAN DONSELAAR K, OUWEHAND P. How to use aggregation and combined forecasting to improve seasonal demand forecasts[J].
International Journal of Production Economics, 2004, 90(2): 151-167.
DOI: 10.1016/j.ijpe.2004.02.004. |
| [28] |
CANIATO F, KALCHSCHMIDT M, RONCHI S, et al. Clustering customers to forecast demand[J].
Production Planning & Control, 2005, 16(1): 32-43.
|
| [29] |
SHENSTONE L, HYNDMAN R J. Stochastic models underlying Croston′s method for intermittent demand forecasting[J].
Journal of Forecasting, 2005, 24(6): 389-402.
DOI: 10.1002/(ISSN)1099-131X. |
| [30] |
LINDSEY M, PAVUR R. Prediction intervals for future demand of existing products with an observed demand of zero[J].
International Journal of Production Economics, 2009, 119(1): 75-89.
DOI: 10.1016/j.ijpe.2009.01.006. |
 2016, Vol. 19
2016, Vol. 19