2. 上海交通大学 机械与动力工程学院,上海 200240
2. School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200240, China
随着社会的发展以及各类突发事件的频发,人们对于科学的应急管理的需求越来越高,医疗应急作为应急管理管理中至关重要的一环,也逐渐得到更多学者的关注。在现有的医疗应急文献中,基于理论分析、经验借鉴和历史教训总结等方式进行的定性研究占绝大多数,主要集中在应急体系构建[1]、应急队伍建设[2]以及基于突发事件类型的医疗应急响应策略[3-5]等问题上。然而也有不少学者将系统仿真、运筹学、优化算法等定量方法运用到医疗应急领域,指导医疗应急决策。例如,Hurwitz等[6]通过建立柔性的仿真平台以及运用运筹学方法和新颖的事件驱动算法,来定量管理医院急诊部门的拥堵问。Li等[7]通过建立多目标数学模型研究了在大规模流感爆发时病人在不同医院之间的最优分配。Alanis等[8]采用二维马尔科夫链模型对医疗应急服务系统(EMS)进行建模,用于计算EMS系统的性能指标。
资源配置是应急响应中的重要问题,有效的资源配置不仅能够减少资源浪费,还能提高伤员救治率和医疗服务水平。部分学者对此类问题进行了研究。Wang等[9]采用基于Agent的仿真来对大规模伤亡事件下的医疗响应进行建模,从而识别出应急方针和资源配置水平对应急处置效果的影响。Araz等[10]通过构建设施选址和线性规划模型研究了在大规模急性传染病爆发时的药品分发点选择和分发点医务人员的最优配置问题。凌思维等[11]在对需求进行分级的基础上研究了灾后医疗物资在各受灾点的最优配置。然而此类文献大多是从全局的角度研究突发事件的医疗应急响应,鲜有针对单个医疗服务机构进行的资源配置研究,且没有将医疗资源的常规需求和应急需求统筹考虑。
为解决突发事故发生时医院常规病人和突发病人之间的资源分配问题,为医院的应急资源配置决策提供定量指导,本文根据系统动力学对整个就诊系统进行了仿真建模。首先根据病人就诊系统内部的病人流转和演化机制得到系统动力学流图,在此基础上,通过对病人就诊过程中关键要素的规律和特征进行分析,构建了病人健康动态、医务人员诊断信心和决策以及基于贝叶斯预测分布的诊断时间和突发病人到达过程等子模型。最后通过仿真实验,对3种不同的资源配置规则进行了比较。
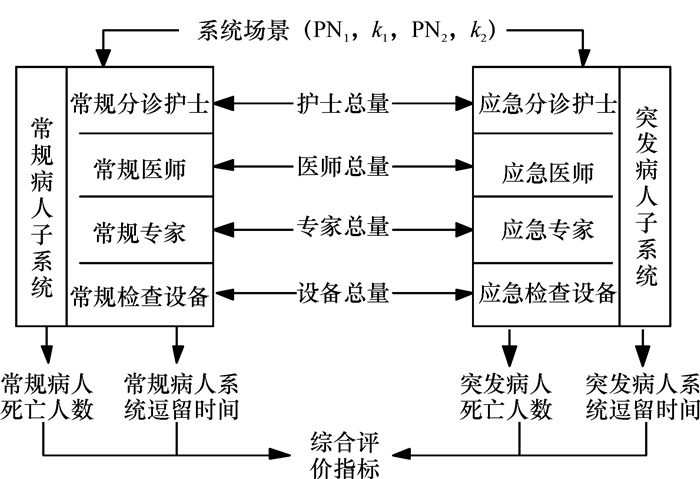
1 系统建模 1.1 问题描述当较大规模的突发事故发生时,医院的突发病人往往会在短时间内大量增加。由于突发病人病情较常规病人更容易恶化,为了尽可能地提高救治水平,医院通常会开通绿色通道用于专门处理突发病人,并暂停对常规病人的接收[12]。与此同时,院内已经挂号的常规病人仍需继续诊断治疗。在这种情况下,整个医疗系统可以看作是由常规病人子系统和突发病人子系统构成,如图 1所示。医疗资源(分诊护士、医师、专家和检查设备)在这两个子系统之间的分配方式会极大地影响整个应急处置效果。图 1中,PN1为常规病人数量,PN2为突发病人规模,k1为常规病人恶化率系数,k2为突发病人恶化率数。
|
图 1 系统资源配置 Fig. 1 System resources allocation |
针对上述问题,本文主要考虑3种资源分配规则。在一定的系统场景下,不同的资源配置规则决定了不同的资源配置方案。为定量地评价不同资源分配规则的优劣,分别对两个子系统进行系统动力学仿真建模,并以系统场景和资源分配方案作为输入,以整个系统的死亡率和所有病人的平均系统逗留时间作为仿真系统的输出,根据仿真输出结果对3种资源分配规则在不同场景下的应急处置效果进行比较。
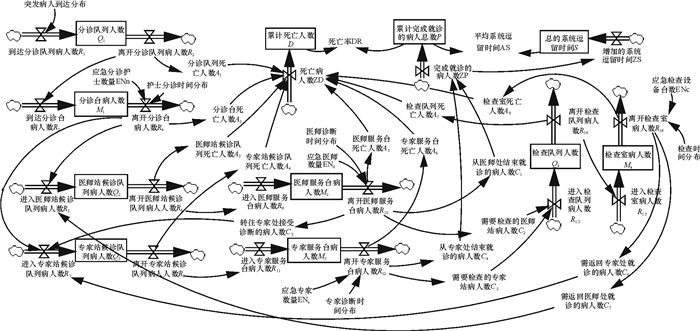
由于突发病人子系统和常规病人子系统的就诊流程基本一致,以突发病人子系统为例,根据突发病人就诊系统的内部流转和演化机制,得到其系统动力学流图,如图 2所示。常规病人子系统动力学流图与此类似。
|
图 2 突发病人子系统动力学流图 Fig. 2 System flow for accident patients |
在该流图中,各关键变量之间的关系表示如下。

|
(1) |
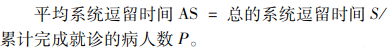
|
(2) |
其中,
累计死亡人数D = INTEG(死亡病人数ZD,0);
死亡病人数ZD =分诊队列死亡人数A1 +分诊台死亡人数A2 +医师站候诊队列死亡人数A3 +专家站候诊队列死亡人数A4 +医师服务台死亡人数A5 +专家服务台死亡人数A6 +检查队列死亡人数A7 +检查室死亡人数A8;
累计完成就诊的病人数P= INTEG(结束就诊的病人数ZP,0);
结束就诊的病人数ZP =从医师处结束就诊的病人数C1 +从专家处结束就诊的病人数C4;
总的系统逗留时间S = INTEG(结束诊断病人的系统逗留时间S,0)。
1.2 子模型构建根据上述系统动力学流图,对突发病人子系统和常规病人子系统中涉及的关键要素建立相应的子模型,包括病人健康动态模型、医务人员诊断和决策模型以及基于贝叶斯预测分布的诊断时间和突发病人到达过程模型。
1.2.1 病人健康动态病人的病情随时间不断恶化,直到死亡或者结束诊断。以δ表示病情恶化率, H0∈[0, 1]表示病人的初始生理状态(H0 = 0表示死亡,H0 = 1表示理想的生理状态),则病人从到达医院至死亡之前的生理状态为H(t) = H0-δt(t为病人等待时间)。综合考虑恶化率和生理状态,定义病人的健康状况RH(t)为
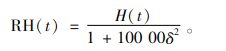
|
(3) |
式中:RH(t)∈[0, 1),δ∈(0, 1)。
1.2.2 医务人员的诊断和决策医务人员的每次诊断都会产生相应的诊断结果和诊断信心,且诊断结果和诊断信心与医务人员的能力水平L和病人的健康状况RH(t)有关。同时,诊断结果和诊断信心决定医务人员的诊断决策。定义分诊护士、医师和专家的能力水平分别为LN = 10,LD = 20,LE = 30。
1) 病情诊断结果DH(t)。
病情诊断结果DH(t)是医务人员对病人健康状况RH(t)的估计。一般来说,医务人员能力越强或病人的健康越接近极端状态(非常严重或者非常健康),诊断结果越准确,误差越小[13]。据此特性,用Beta分布来描述医务人员对病人的病情诊断结果,令DH(t)服从众数为RH(t)的Beta分布,另一形状参数为能力水平L。那么诊断结果DH(t)的方差为
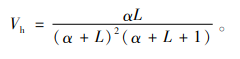
|
(4) |
其中
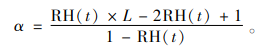
|
(5) |
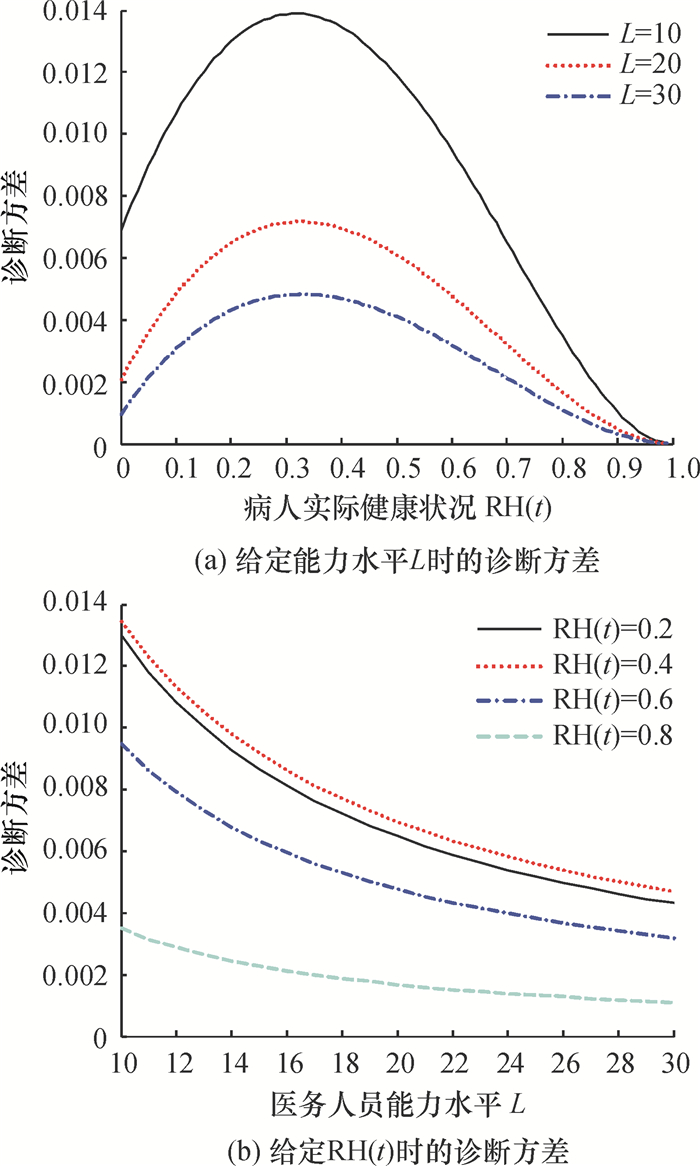
诊断结果的方差Vh与医务人员的能力水平L和病人的健康状况RH(t)的关系如图 3所示。
|
图 3 诊断方差与L和RH(t)的关系 Fig. 3 Diagnostic variance under given L or RH(t) |
2) 医务人员的诊断信心DC(t)。
同样,医务人员的能力越强或病人的健康越接近极端状态,诊断信心越强且信心方差越小[13]。用Beta分布来描述医务人员的诊断信心,令诊断信心DC(t)服从众数为DC_m(t)的Beta分布,形状参数为能力水平L,众数DC_m(t)的表达式为
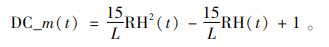
|
(6) |
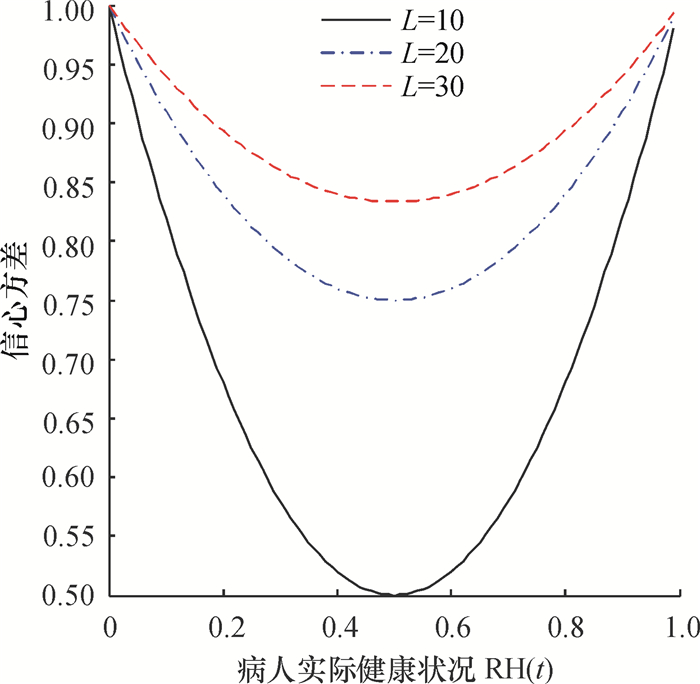
式(6)表明,RH(t)越接近0和1,信心众数越大;L越大,信心众数越大,如图 4所示。
|
图 4 信心众数与RH(t)和L的函数关系 Fig. 4 Relations Hetween confidence mode and L, RH(t) |
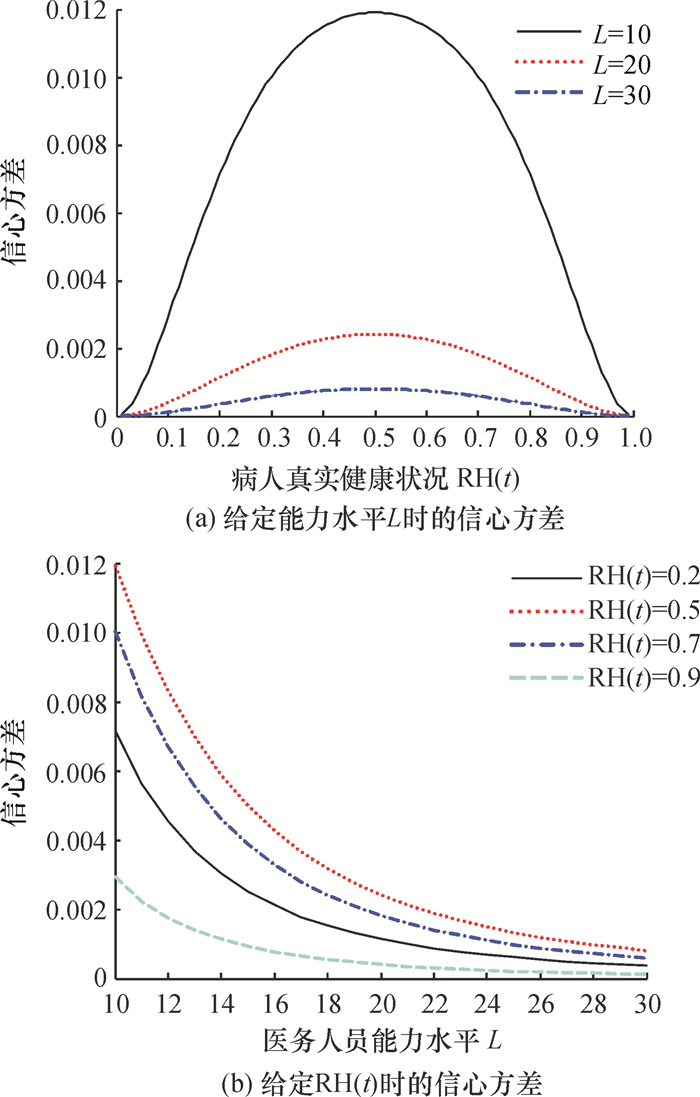
能力水平L和病人健康状况RH(t)对医务人员的信心方差的影响则如图 5所示。
|
图 5 信心方差与L和RH(t)的关系 Fig. 5 Confidence variance under given L or RH(t) |
3) 诊断决策。
分诊护士根据自己对病人的诊断结果和诊断信心将病人进行分流,将病情较严重或者诊断信心不足的病人分流到专家处,其余的病人则分流到医师处。采用综合指标SI来考量分诊护士的诊断决策:
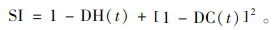
|
(7) |
式中:DH(t)∈(0, 1), DC(t)∈(0, 1), SI∈(0, 2)。当SI大于阈值SI*时,此时病人被分流至专家处;SI小于SI*时,病人被分流至医师处。
医师接收病人后,根据诊断结果和信心有如下决策。
1) 诊断信心DC(t)大于等于医师的信心阈值Cd*时,医师根据诊断结果DH(t)落入的区间范围作出相应的诊断决策(抢救、留观、住院和开处方),病人处理完成。
2) 诊断信心DC(t)小于医师信心阈值Cd*,且病人没有接受过辅助检查时,则病人需要前往检查站接受辅助检查,检查完成之后返回接受二次诊断。
3) 诊断信心DC(t)小于医师的信心阈值Cd*,且病人已经接受过辅助检查时,该病人将被转到专家处接受进一步诊断。
专家的诊断过程与医师类似,然而由于专家的能力水平最高,当专家对病人的诊断信心Ce*不足且病人已经进行过辅助检查时,专家必须作出最终的诊断决策。
1.2.3 突发病人到达过程和各服务站诊断时间由于医院缺乏突发事故病人到达的历史数据,难以使用经典的点估计和经验频率分布来模拟突发病人的到达过程,因而采用贝叶斯预测分布来描述突发事故病人的到达时间间隔。令AI(arrival interval)表示突发事故病人的到达时间间隔。根据常见的病人到达随机过程,令AI服从参数为λ(未知)的指数分布,λ的先验分布为参数为a和b的Gamma分布,参数a和b根据主观先验信息确定。由于Gamma分布是指数分布参数λ的共轭分布,在给定AI的一些观测数据AI =(ai1,ai2,ai3,…,ain)后,可以得到λ的后验分布为a′=a+n和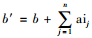
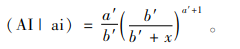
|
(8) |
相比于直接采用指数分布而言,后验预测分布融合了主观先验信息,并能够随着观测数据的增加不断对分布进行更新,使之更加接近实际的病人到达过程。
类似地,对于病人(包括突发病人和常规病人)在各个服务站的服务时间,也采用贝叶斯预测分布。用ST(service time)表示病人在某服务站的服务时间,不失一般性,令ST服从均值为Ξ,精度为Λ的正态分布,其中Ξ和Λ均未知。假定Ξ和Λ服从无信息的联合先验分布为:π(Ξ, Λ)=1/Λ, Λ > 0[15]。在给定ST的部分观测值st=(st1, st2, st3, ……stn)之后,可得到Ξ和Λ的后验分布如下:Ξ服从参数为st、(n-1)/s2、自由度为n-1的t分布,Λ则服从参数为(n-1)/2和ns2/2的Gamma分布(st为样本均值,s2为样本方差)。进而根据贝叶斯条件概率可求得ST的后验预测分布为
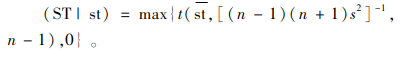
|
(9) |
在式(9)中,由于服务时间不可能为负,故舍弃相应的负值。
2 模型仿真与结果分析在对上述就诊系统进行建模的基础上,输入资源分配方案,通过运行系统仿真,会输出病人平均系统逗留时间AS(average stay)和死亡率DR death rate)两个指标,进一步构建如下综合评价指标:
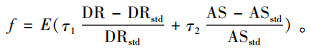
|
(10) |
式中:DRstd,ASstd是死亡率和平均系统逗留时间的参考值。τ1, τ2则是上述两个评价指标偏离参考值的惩罚系数。E表示数学期望,由于仿真的随机性,在同一资源分配方案下,仿真的输出结果也会随机波动,故采用期望值表示。
2.1 仿真实验设定和模型验证以上海市某三甲医院为研究对象,进行仿真初始设定。
1) 资源总量。分诊护士9人,医师12人,专家8人,辅助检查设备4台。
2) 病人特征。病人的初始生理状态H0~ uniform[0.5, 1),由于病人从到达医院到死亡的时间大部分介于10 min到1 000 min之间,令δ0~ 0.01×Beta (2, 2),常规病人的恶化率为δ1 = k1×δ0, 突发病人的恶化率δ2 = k2×δ0。其中,k1,k2为恶化率系数,表征常规病人和突发病人整体病情的严重程度。
3) 突发病人到达过程。由于没有具体的观测数据,突发病人的到达时间间隔采用无观测数据的贝叶斯预测分布,即a′=a, b′=b。根据经验确定先验参数为a = 42.2, b = 21.3。
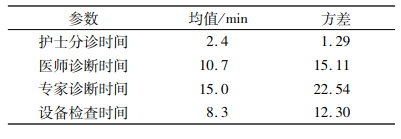
4) 服务时间。病人在各服务站服务时间采用有观测数据的后验预测分布,分别在医院各服务站随机抽取n = 100个病人,统计其在各服务站的诊断时间,得到如表 1所示数据,进一步可得到病人在各服务站服务时间的贝叶斯预测分布为:护士分诊时间STn~ max{t(2.4, 1.32, 99), 0}, 医师诊断时间STd~ max{t(10.7, 15.4, 99), 0}, 专家诊断时间STe~ max{t(15.0, 23.0, 99), 0}, 辅助检查时间STc~ max{t(8.3, 12.5, 99), 0}。
| 表 1 服务时间数据统计 Tab. 1 Statistical data for service time |
5) 诊断阈值。根据护士分流比例、病人需要接受辅助检查的比例、病人不同最终去向比例等实际系统关键参数,反复运行仿真模型,调整阈值参数,使得模型中的概率与实际情况大致一致。得出最终的阈值参数为SI* = 1.1,Cd* = 0.85,Ce*= 0.71。
为验证模型的有效性,分别改变常规病人子系统和突发病人子系统的关键变量如资源数量、病人恶化率、病人数量等,系统输出的死亡率和病人系统逗留时间的变化趋势与真实系统一致,证明了模型的有效性。同时,为保证仿真结果的可靠性,采用终止型序贯程序法确定仿真次数以确保仿真输出值置信度为90%,置信区间半宽小于点估计的15%.
2.2 资源分配规则比较针对不同的系统场景,通过仿真,对3种资源分配规则进行比较。
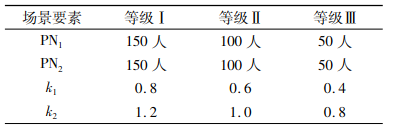
根据常规病人和突发病人的规模以及病人恶化率系数考虑不同的系统场景,场景要素包括:常规病人数量PN1、常规病人恶化率系数k1、突发病人规模PN2和突发病人恶化率系数k2。其中,常规病人的数量PN1表示突发事件发生时系统中未完成诊断的常规病人数,而突发病人规模PN2则表示在突发事件发生后前来医院就诊的病人总数。将每个要素定性地分为3个等级,如表 2所示,通过4种要素的不同组合共构建34=81种场景。
| 表 2 场景要素及其等级 Tab. 2 Scene elements grading |
在常规病人和突发病人之间进行资源分配的规则考虑以下3种。
规则1 根据系统中常规病人的数量PN1和突发病人的数量PN2的比值进行资源分配, 病人数量越多分配的资源也越多。
规则2 根据常规病人的恶化率系数k1与突发病人的恶化率系数k2的比值进行资源分配。恶化率系数越大,分配的资源数量越多。
规则3 综合考虑常规病人和突发病人的数量和恶化率,以如下方式进行资源分配:
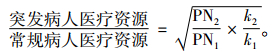
|
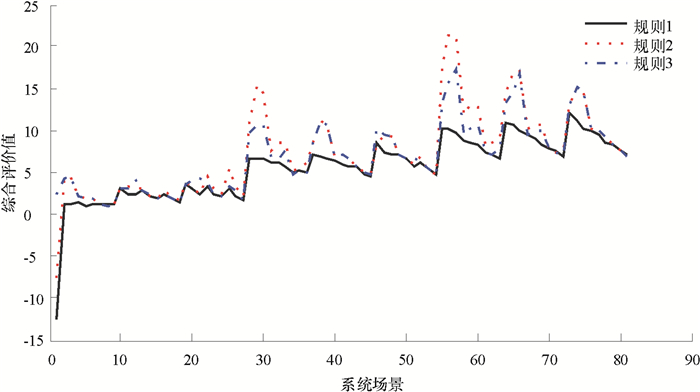
在不同场景下依据3类资源分配规则得到的资源分配方案的仿真结果如图 6所示。
|
图 6 不同场景下3类资源配置规则的系统性能 Fig. 6 System performance under three resources allocation rules in different scenes |
从图 6中可以看出,在不同的系统场景下,3种规则对应的仿真结果的差别变化也很大,但根据突发病人和常规病人的病人规模之比进行资源分配(规则1)几乎在所有的场景中都具有最优的应急处置效果。相比之下,根据病情恶化率之比(规则2)得到的仿真结果在大部分场景下都比另外两种规则差,而综合考虑病人规模和恶化率(规则3)则能够得到介于规则1和规则2之间的应急处置效果。这说明在病人恶化率和病人规模这两个因素中,常规病人和突发病人在数量上的差异是决定医疗资源分配的主要因素,而恶化率为次要因素。因此,针对本文所解决的问题,参考常规病人和突发病人的规模来进行应急资源分配决策是相对明智的做法。
3 结论在研究突发事件下医疗系统中的资源分配问题时,通过对医疗系统进行系统动力学建模仿真,解决了难以用解析的方式进行数学建模的医疗资源分配方案的评价问题。在建模过程中,考虑了病人病情的实时变化和医务人员的诊断信心与决策,并采用贝叶斯预测分布来描述医务人员的评估时间和突发病人的到达时间间隔。通过仿真实验,对不同的资源配置规则进行了比较,证明了基于病人规模的资源分配规则具有更好的应急处置效果。本文的研究对于医疗机构的应急资源分配决策提供支持也为应急预案的制定提供了依据。
| [1] |
刘铁民. 应急预案重大突发事件情景构建——基于"情景-任务-能力"应急预案编制技术研究之一[J].
中国安全生产科学技术, 2012, 8(4): 5-12.
LIU T M. Study on scenes' construction of emergency planning--part 1 of emergency planning technology based on "scene-task -ability"[J]. Journal of Safety Science and Technology, 2012, 8(4): 5-12. |
| [2] |
JONES D A, BAGSHAW S M, BARRETT J, et al. The role of the medical emergency team in end-of-life care: a multicenter, prospective, observational study[J].
Critical care medicine, 2012, 40(1): 98-103.
|
| [3] |
ZHANG L L, LIU X, LI Y P, et al. Emergency medical rescue efforts after a major earthquake: lessons from the 2008 Wenchuan earthquake[J].
The Lancet, 2012, 379(9818): 853-861.
DOI: 10.1016/S0140-6736(11)61876-X. |
| [4] |
石胜蓉. 群体性突发事件应急救援的"一体化模式"[J].
重庆医学, 2011, 40(16): 1612-1613.
SHI S Y. "Integration model" for massive emergency rescue[J]. Chongqing Medicine, 2011, 40(16): 1612-1613. DOI: 10.3969/j.issn.1671-8348.2011.16.021. |
| [5] |
WOOLHOUSE M E J, RAMBAUT A, KELLAM P. Lessons from Ebola: improving infectious disease surveillance to inform outbreak management[J].
Science translational medicine, 2015, 7(307): 307rv5.
DOI: 10.1126/scitranslmed.aab0191. |
| [6] |
HURWITZ J E, LEE J A, LOPIANO K K, et al. A flexible simulation platform to quantify and manage emergency department crowding[J].
BMC Medical Informatics and Decision Making, 2014, 14(1): 1-11.
DOI: 10.1186/1472-6947-14-1. |
| [7] |
SUN L, DEPUY G W, EVANS G W. Multi-objective optimization models for patient allocation during a pandemic influenza outbreak[J].
Computers & Operations Research, 2014, 51: 350-359.
|
| [8] |
ALANIS R, INGOLFSSON A, KOLFAL B. A Markov chain model for an EMS system with repositioning[J].
Production and Operations Management, 2013, 22(1): 216-231.
DOI: 10.1111/poms.2012.22.issue-1. |
| [9] |
WANG Y, LUANGKESORN K L, SHUMAN L. Modeling emergency medical response to a mass casualty incident using agent based simulation[J].
Socio-Economic Planning Sciences, 2012, 46(4): 281-290.
DOI: 10.1016/j.seps.2012.07.002. |
| [10] |
ARAZ O M, FOWLER J W, NAFARRATE A R. Optimizing service times for a public health emergency using a genetic algorithm: locating dispensing sites and allocating medical staff[J].
IIE Transactions on Healthcare Systems Engineering, 2014, 4(4): 178-190.
DOI: 10.1080/19488300.2014.965394. |
| [11] |
凌思维, 杨斌, 孙少文. 基于需求分级的应急医疗资源配置[J].
广西大学学报(自然科学版), 2014, 39(2): 358-364.
LING S W, YANG B, SUN S W. Emergency medical resources allocation based on demand hierarchy[J]. Journal of Guangxi University(Natural Science Edition), 2014, 39(2): 358-364. |
| [12] |
ABIR M, CHOI H, COOKE C R, et al. Effect of a mass casualty incident: clinical outcomes and hospital charges for casualty patients versus concurrent inpatients[J].
Academic Emergency Medicine, 2012, 19(3): 280-286.
DOI: 10.1111/acem.2012.19.issue-3. |
| [13] |
WANG S, HOLLOWAY L E, DEPRIEST P, et al. Analysis of Hospital Rapid Response Protocols Using Simulation [C/OL].(2012-08-20). http://xueshu.baidu.com/s?wd=paperuri%3A%28b219323226d386f5e68e008be219e7a7%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Ficp.jsp%3Farnumber%3D6386403&ie=utf-8.
|
| [14] |
DEGROOT M H. Optimal statistical decisions [M]. NY:John Wiley & Sons, 2005.
|
| [15] |
MORTON D P, POPOVA E. A Bayesian stochastic programming approach to an employee scheduling problem[J].
IIE Transactions, 2004, 36(2): 155-167.
DOI: 10.1080/07408170490245450. |
 2016, Vol. 19
2016, Vol. 19