随着物流技术的飞快发展,企业之间的竞争也越来越激烈,每个企业为了提升自己的竞争力,都在寻求一种适合自身发展的供应链管理策略,如越库(cross-docking)、供应商管理库存、物流配送网络优化等。越库是一种高效快速的调度策略,货物从入库货车被直接转运至出库货车,在越库中心停留的时间不超过24 h,有时甚至会缩短到1 h内。这不仅加快了顾客响应时间,提高了服务质量,而且也减少了货物的储存成本。很多大型企业(如沃尔玛、UPS、丰田等[1-3])都已采用越库策略优化供应链流程,越库已成为仓库管理的主流技术[4]。
越库策略的成功实施关键取决于有效的车辆调度,即货车的仓门分配和排序决策,它直接决定了入库货车和出库货车是否最佳协调、货物是否能快速通过越库中心。目前,国内外相关文献大多研究单仓门环境下的越库车辆调度。文献[5]研究两台机越库流水车间调度问题,在证明该问题是NP难问题的基础上,提出了基于Johnson规则的启发式算法和分支定界算法。文献[6]研究以带权总完工时间为目标的相同问题,提出逆向动态规划算法, 并证明算法至少可以求解25个工件规模的问题。文献[7]研究了运输时间非对称不确定性条件下的越库调度问题,以最小化完工时间为目标建立了混合整数规划模型,提出了期望值修正算法和基于修正期望值的启发式算法。文献[8]研究考虑缓存区的越库车辆调度问题,提出9种优化车辆停靠顺序的排序策略,使停留在缓存区的货物总数最小化,来达到最小化完工时间的目的,并设计了启发式求解算法。文献[9]采用文献[8]的算法所得解为起点,提出解决上述问题的差分进化算法、遗传算法、粒子群算法、禁忌搜索算法和蚁群算法,数值实验证明所提的差分进化算法性能最优。文献[10]则提出两种组合差分进化算法,并证明其优于典型的差分进化算法。文献[11]研究以最小化越库操作总时间和入库货车延迟时间为目标的车辆排序优化问题,设计了3个多目标算法进行求解。
多仓门环境下的越库车辆调度问题研究相对较少。如文献[12]研究以最小化货物在越库中心的传送距离为目标的货车仓门分配问题,并设计分散搜索算法解决问题。文献[13]研究出库货车的离开时间限于一定时间窗的入库货车调度问题,提出6种元启发式算法,通过数值实验说明蚁群算法的性能较好。文献[14]研究货物装卸带有时间窗,并且越库中心容量有限的入库货车调度问题,以最小化操作成本和惩罚成本为目标,设计禁忌搜索算法和遗传算法来优化问题。文献[15]对文献[14]的研究问题进行扩展,考虑货车到达和离开有时间窗限制,并设计自适应禁忌搜索算法进行求解。文献[16]和[17]针对入库和出库货车的仓门分配和顺序优化问题,分别设计了邻域搜索算法和遗传算法进行求解。
越库车辆调度的现有文献都考虑自由装卸方式,即货车上的货物按任意顺序装卸,这比较符合货物批量大、种类少的情形。随着顾客需求越来越多样化,货物的批量变少而种类变多,货车单次接收的供应商数量或配送的顾客数量变多。这时货车的取货、送货顺序通常是固定的,这就决定了入库货车和出库货车上的货物存在卸载和装载顺序要求。这不仅增加了仓门分配和车辆调度的限制因素,使组合优化难度增加,而且容易放大由于调度不当引起的各种效率低下现象。例如,造成出库货车在装运仓门处等待时间加长,延长越库总操作时间,或者货物在运转中心储存时间加长,增加货物储存成本等。
本文针对上述实际问题,首先建立考虑货物装卸顺序要求的越库车辆调度数学规划模型,并提出改进粒子群算法(ω-PSO)进行求解。最后通过不同规模的数值实验,把改进粒子群算法的求解结果与标准粒子群算法(PSO)和遗传算法(GA)的求解结果进行对比分析,验证所建模型的正确性和设计算法的有效性。
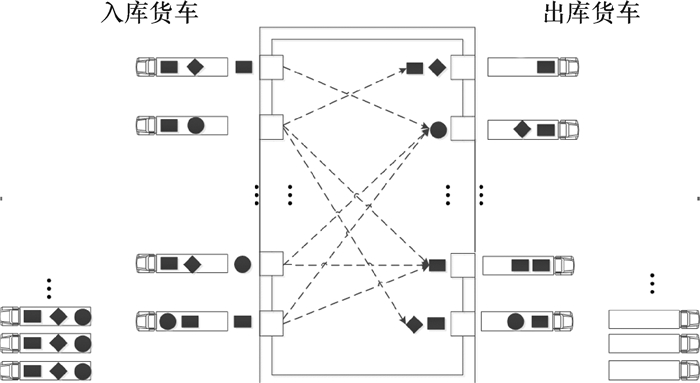
1 问题描述及模型设计 1.1 问题描述越库调度系统的结构如图 1所示。越库配送中心有多辆货车和多个仓门,并且货车数量大于仓门数量,货物从入库货车上卸载下来,在配送中心进行扫描、分拣等操作后,马上装运到出库货车上。货物的装卸顺序需按照货物在货车上的排列顺序进行,决策者需要决策每辆货车分配到哪个仓门,以及货车按什么次序停靠到指定仓门进行卸货或者装货。
|
图 1 越库系统结构图 Fig. 1 The framework of a cross docking system |
所研究问题有以下假设:1)所有仓门同时只能停靠1辆货车;2)货车一旦停靠,需等待货车上的所有货物卸载或者装载完毕后才能离开;3)货物只有在货车停靠仓门后才可以进行装卸;4)所有货物的单位卸载或装载时间相同;5)每辆货车同时只能装卸1个货物;6)每种货物只有1个。
1.2 数学模型为上述问题建立整数线性规划模型,模型中用到的数学符号如下。
M为入库货车数量;
N为出库货车数量;
O为接收仓门数量;
P为装运仓门数量;
K为货物种类数量;
Sop为货物从接收仓门o转运到装运仓门p所需时间;
T为完工时间,从第一辆入库货车开始卸载货物到最后一辆出库货车完成装载货物的时间;
d为货车交换时间;
t为单位货物的卸载/装载时间;
CTm为入库货车m的停靠时间;
DTn为出库货车n的停靠时间;
FTm为入库货车m的离开时间;
LTn为出库货车n的离开时间;
GTk为货物k开始卸载的时间;
HTk为货物k开始装运的时间;
Z为一个大数;
rmk表示如果入库货车m上有货物k则为1,反之为0;
snk表示如果出库货车n上有货物k则为1,反之为0;
amkk′表示如果货物k比货物k′后从入库货车m上卸载下来则为1,反之为0;
bnkk′表示如果货物k比货物k′后装上出库货车n则为1,反之为0。
决策变量:
ymo表示如果入库货车m分配到接收仓门o则为1,反之为0;
znp表示如果出库货车n分配到装运仓门p则为1,反之为0;
pmm′o表示如果分配到接收仓门o的入库货车m比入库货车m′后停靠则为1,反之为0;
qnn′p表示如果分配到装运仓门p的出库货车n比出库货车n′后停靠则为1,反之为0。
数学模型:
min T。
s.t.
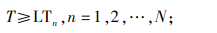
|
(1) |
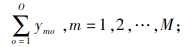
|
(2) |
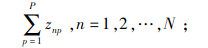
|
(3) |
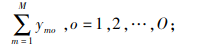
|
(4) |
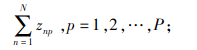
|
(5) |
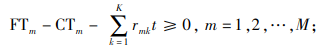
|
(6) |
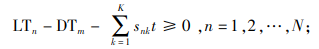
|
(7) |
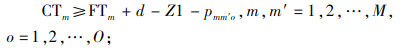
|
(8) |
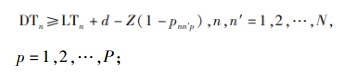
|
(9) |
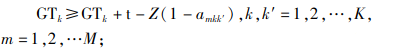
|
(10) |
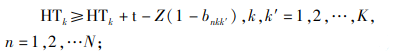
|
(11) |
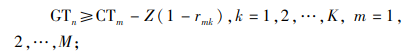
|
(12) |
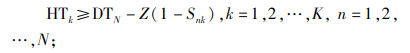
|
(13) |
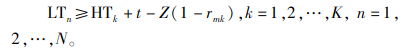
|
(14) |
约束(1)表明完工时间的取值范围;约束(2)和(3)保证每辆货车只可以分配1个仓门;约束(4)和(5)规定每个仓门都必须参与调度;约束(6)和(7)保证入库货车和出库货车一旦停靠必须等待自身货物装卸完毕才能离开;约束(8)和(9)表明每个仓门同时只可以停靠1辆货车;约束(10)和(11)保证货物按既定次序装卸,即每件货物只能在它之前的货物卸载或装载完毕后才开始卸载或装载;约束(12)、(13)和(14)联合定义了货车之间发生转运关系的必要条件。
2 算法设计 2.1 标准粒子群算法介绍粒子群优化算法(particle swarm optimization,PSO)模拟鸟群集体觅食的行为,通过粒子之间的协作,使群体达到最优目标。它是一种基于群体迭代的、在解空间里追随最优粒子进行搜索的算法。其基本原理是在D维空间中,有Q个粒子, xi=(xi1, xi2, …, xiD)表示第i个粒子的位置,把xi代入适应函数f(xi)可求得适应值,vi=(vi1, vi2, …, viD)表示第i个粒子的飞行速度, Pbesti=(Pbesti1, Pbesti2, …, PbestiD)表示第i个粒子经历过的最好位置, Gbestg=(Gbestg1, Gbestg2, …, GbestgD)表示种群所经历过的最好位置。每一次粒子飞行速度的迭代过程都按照式(15)进行更新:
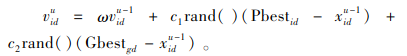
|
(15) |
其中ω为惯性权重,用来调节对解空间的搜索范围;c1和c2为学习因子,用于调整粒子的自身经验与社会经验在其运动过程中起到的作用;rand()为(0, 1)之间均匀分布的随机数,增强搜索的随机性;u为当代迭代次数。根据式(16)可以计算每个粒子更新后的位置:
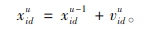
|
(16) |
通常情况下,粒子的飞行速度被限制在[-vmax, vmax]内,位置被限制在[-xmax, xmax]内,当飞行速度或者位置超过这个值域时,则取临界值,防止粒子在迭代过程中飞离搜索空间。
2.2 ω-PSO设计 2.2.1 惯性权重的改进在粒子群算法中,惯性权重起着权衡全局搜索和局部搜索的作用。当惯性权重较大时,算法倾向于全局搜索,当惯性权重较小时,算法倾向于局部搜索。为了使算法能够更好地平衡全局搜索和局部搜索,本文采用动态地改变惯性权重的方法,达到动态调整算法搜索能力的作用。
目前,大多数文献针对于惯性权重的改进都是线性的改变,如文献[18]。但粒子群算法搜索过程是非线性且复杂的,从全局搜索到局部搜索的线性变化并不能真实地反应搜索全局最优解所需的搜索过程[19]。因此,本文对惯性权重进行非线性改进,由于算法在前期需要较大的惯性权重值来扩大算法搜索范围,在后期需要较小的惯性权重来搜索最优解,结合余弦函数曲线特性,本文提出惯性权重按照式(17)进行非线性改变的策略来优化问题。
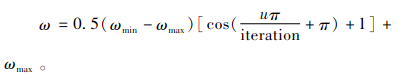
|
(17) |
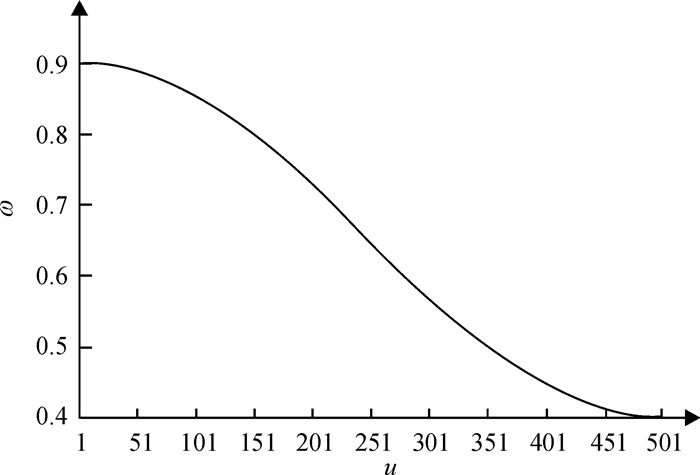
其中ωmax为初始权重,ωmin为最终权重,u为当代迭代次数,iteration为最大迭代次数,本文中ωmax的值为0.9,ωmin的值为0.4,iteration的值为500,ω的动态变化曲线如图 2所示。与线性改变策略相比较,本文提出的改变策略让惯性权重在算法初期和后期变化更加平缓,使算法在前期全局搜索能力更强,在后期局部搜索最优解能力也更强。
|
图 2 惯性权重变化曲线 Fig. 2 The change curve of inertia weight |
本文按照入库和出库两个部分对粒子进行编码。对于每个粒子,位置编码为两个A维向量:Xv和Xr,其中,A对应于入库部分的货车数M或出库部分的货车数N,Xv的每一维分别表示每个货车分配的仓门编号,Xr的每一维分别表示每个货车的停靠次序,同时,粒子的速度也编码成两个A维向量Vv和Vr。这种方式虽然使问题的维数增加,但这并不会增加改进粒子群算法计算的复杂性,这一点通过在后文与遗传算法进行对比得以验证。
2.2.3 初始解集的建立位置向量Xv的每一维随机取[1, B]之间的整数,其中,B对应于入库部分的接收仓门数O或出库部分的装运仓门数P。为了满足模型中每个仓门都必须参与调度的约束条件Xv,需包含[1, B]之间的所有整数,否则,重新初始化该位置向量。位置向量Xr从第1维开始依次在[1, A]之间产生不同的随机实数,然后,按照这些实数从小到大的顺序来确定货车的停靠次序。速度向量Vv的每一维随机取[-(B-1), (B-1)]之间的实数,Vr的每一维随机取[-(A-1), (A-1)]之间的实数。这种方式保证初始粒子群的每个粒子都是可行解,为后续优化减少了不必要的计算,提高了算法的运行效率。
2.2.4 整数规范原则基本粒子群算法主要针对连续函数进行搜索运算。而越库车辆的仓门分配和排序问题属于离散组合优化问题。为此,本文提出整数规范原则,对算法进行离散化。
在更新粒子位置向量时,Xv向下取整,Xr按照值从小到大的顺序依次重新取值1, 2, …, A。例如,8辆货车、4个仓门的问题,经过迭代后位置向量如表 1所示,进行整数规范后的位置向量如表 2所示。它对应的解为:货车1分配到仓门3, 停靠次序为1;货车2分配到仓门2, 停靠次序为3;货车3分配到仓门3, 停靠次序为7;货车4分配到仓门3, 停靠次序为2;货车5分配到仓门4, 停靠次序为8;货车6分配到仓门1, 停靠次序为4;货车7分配到仓门1, 停靠次序为5;货车8分配到仓门2, 停靠次序为6。
| 表 1 迭代后的位置向量 Tab. 1 The position vector after iterating |
| 表 2 整数规范后的位置向量 Tab. 2 The position vector after integer coding |
在迭代过程中,由于父代粒子飞行的方向和距离具有一定的随机性,因此子代中一些粒子的Xv向量可能没有包含1~B的所有整数,即有的仓门没有分配货车,这种解称之为非可行解。针对这种情况,本文采用替换策略对非可行解进行修复:首先找出非可行解中未被分配货车的仓门,然后找出该仓门在粒子局部最优解中所分配的货车及次序,用它们替换掉非可行解中相同位置的部分,最后对因此造成重复的货车次序进行调整。假设粒子i迭代后成为非可行解,如表 3所示,仓门2未被分配货车。该粒子的局部最优解如表 4所示,将其中的仓门2所分配的货车及其次序替换掉表 3中相同位置的部分,即原来分配到4号仓门的货车2和货车5调整到仓门2,且次序分别修改为3和5。这时,货车6和7的次序需要由3和5调整成4和8。修复后粒子i的位置向量如表 5所示。通过这种方法,在剔除非可行解的同时也使得粒子从局部最优解遗传到优秀信息,提高算法的运算效率。
| 表 3 粒子i的位置向量 Tab. 3 The position vector of particle i |
| 表 4 粒子i的局部最优解位置向量 Tab. 4 The local best position vector of particle i |
| 表 5 修复后的粒子i的位置向量 Tab. 5 The right position vector of particle i |
本文研究的是最小值优化问题,完工时间越短,粒子适应值越高。单个粒子的适应值
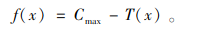
|
(18) |
式中, Cmax是预先指定的一个较大的数,T(x)为该粒子完工时间,其计算方法详述如下。
入库货车m的停靠时间
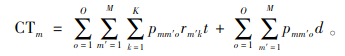
|
(19) |
在式(19)中,入库货车m的停靠时间由两部分组成:1)和入库货车m分配在同一个仓门,且比入库货车m先停靠的货车上货物的卸载时间之和;2)入库货车m停靠之前,其所在仓门处货车的交换时间之和。当入库货车m为第一个停靠接收仓门时,CTm的值为0。
在模型中,货物是连接出库货车和入库货车的关键因素,在计算完工时间时,货物的装卸时间也起着至关重要的作用。货物k开始卸载时间GTk和开始装载时间HTk分别按照式(20)和式(21)计算。

|
(20) |
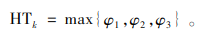
|
(21) |
其中,
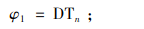
|
(22) |
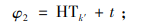
|
(23) |
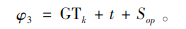
|
(24) |
式(20)中,货物k的开始卸载时间分两种情况:
1) 若货物k第1个从货车m上卸载时,其开始卸载时间为货车m的停靠时间;
2) 若货物k不是第1个从货车m上卸载时,其开始卸载时间为其前面1个货物k′的开始卸载时间加上货物k′卸载所需时间。
式(21)中,货物k的开始装载时间分3种情况:
1) 若货物k在装运仓门处等待被装载,且它是出库货车n的第1件货物,则它的开始装载时间等于出库货车n的停靠时间,即为φ1;
2) 若货物k在装运仓门处等待被装载,但不是第1件待装货物,则其开始装载时间等于其前面一个货物的开始装载时间加上货物k′装载所需时间,即为φ2;
3) 若出库货车等待货物k从接收仓门o转运到装运仓门p处再进行装载,则货物k的开始装载时间等于其开始卸载时间、卸载时间和仓门间运输时间之和,即为φ3。φ1、φ2和φ3分别按照式(22)、(23)和(24)计算。
出库货车n的离开时间按照式(25)计算。
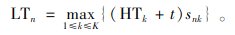
|
(25) |
式(25)中,出库货车n的离开时间为出库货车n上最后一个货物k的开始装载时间加上该货物装载所需时间。最后一辆出库货车的离开时间即为越库操作的完工时间。
2.2.7 交叉操作在粒子群算法中,最优个体控制了种群的搜索方向,所有粒子在飞行过程中都向最优个体靠拢,使得种群容易陷入局部最优,为了保持种群的多样性,本文对粒子进行交叉操作。在算法迭代过程中,若全局最优粒子Gbestg连续e代未发生改变,则根据每个粒子适应值的大小,把种群分成各占一半的精英种群和交叉种群,并对交叉种群中的粒子进行交叉操作,精英种群保持不变,这样使得算法在搜索过程中恢复了种群多样性的同时也保留了质量优秀的粒子。交叉过程采用单点交叉方式,例如对粒子i和j进行交叉时,在(1, A)之间随机产生1个整数f,分别把粒子i的位置向量Xv、Xr和速度向量Vv、Vr中f维之后的部分与粒子j相应部分进行互换,得到新的粒子i′和j′。
2.2.8 算法步骤1) 初始化问题参数,生成初始解集;
2) 计算粒子适应值,并根据粒子适应值更新局部最优解和全局最优解;
3) 判断是否满足交叉操作条件,满足则进行交叉操作,不满足则直接进行下一步操作;
4) 根据式(17)更新惯性权重ω;
5) 根据式(15)、(16)更新粒子位置和飞行速度(实数向量);
6) 把所有粒子位置向量按照整数规范原则进行修改(整数向量);
7) 对子代中不可行解进行修复;
8) 判断是否满足终止条件,满足则结束,否则转到步骤2)。
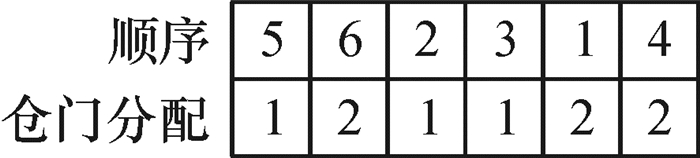
2.3 遗传算法设计要点 2.3.1 染色体编码遗传算法采用自然数编码,根据所研究问题的特点,构造双层基因染色体,第1层表示货车顺序,第2层表示货车分配的仓门。图 3为货车数为6、仓门数为2的染色体构造示意图。
|
图 3 染色体构造示意图 Fig. 3 The sketch map of chromosome |
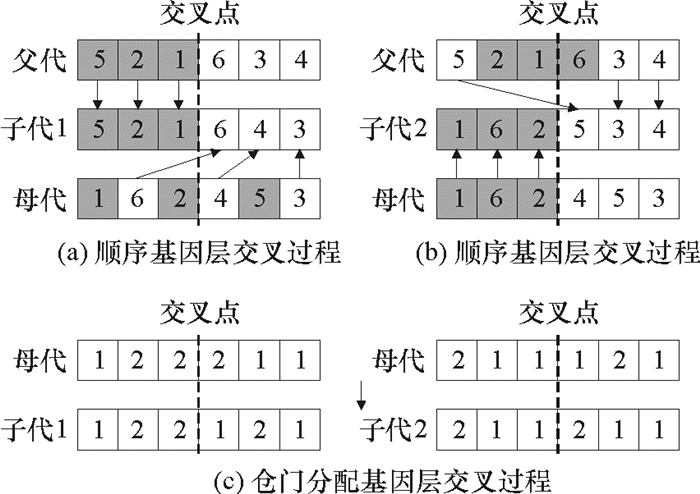
交叉过程采用单点交叉方式,随机产生1个交叉点,将父代染色体划分为两部分。针对顺序基因层,子代1中的第1部分为父代的第1部分,第2部分由母代中与父代第1部分相异基因组合而成,子代2的产生过程与子代1类似,第1部分为母代第1部分,第2部分由父代中与母代第1部分相异基因而成,图 4(a)和(b)表示了两个染色体顺序基因层交叉操作过程。针对仓门分配基因层,子代1由父代第1部分和母代第2部分组成,子代2则相反,如图 4(c)所示。
|
图 4 交叉操作 Fig. 4 The cross-over operation |
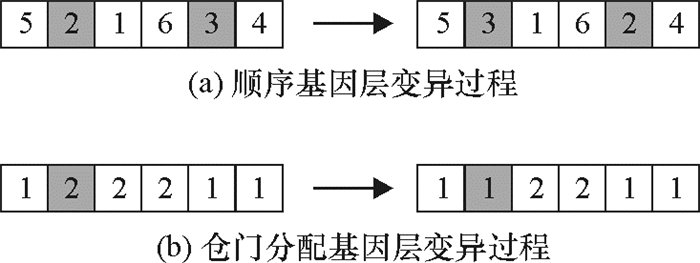
在变异过程中,顺序基因层采用互换变异方式,随机选择两个基因位,将它们的值进行互换;仓门分配基因层采用单点变异方式,随机选择1个基因位,采用[1, B]之间随机产生的异于该基因位原值的随机整数进行替换,父代染色体的变异过程如图 5所示。
|
图 5 变异操作 Fig. 5 The mutation operation |
由于本文研究的越库车辆调度问题在国际上尚无标准测试数据,本文根据实际情况随机产生大量的实验数据来验证ω-PSO算法的有效性。所有实验均在Intel Core i3-3240 CPU@3.40GHz 4.0G内存的计算机上进行,算法均用VC++6.0语言编写。
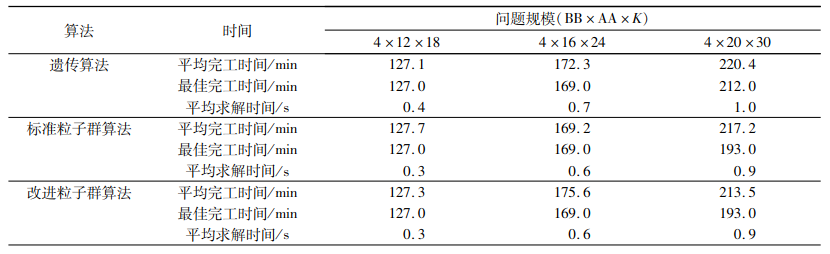
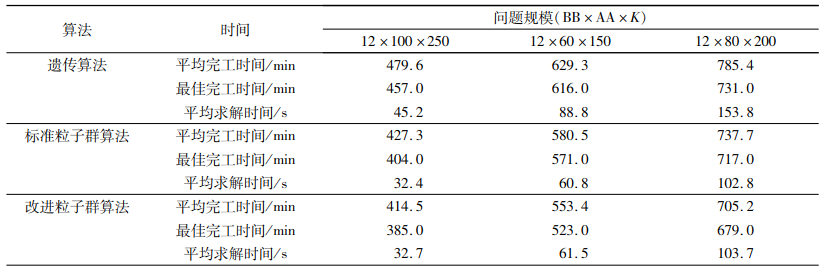
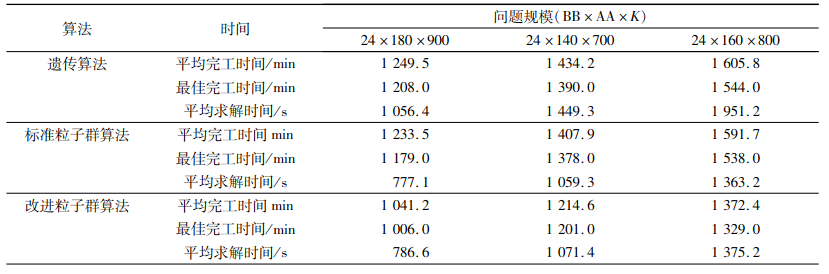
根据仓门总数、货车总数、货物种类数的不同将问题分为小、中、大3个规模,每个规模分别用GA、PSO、ω-PSO三种算法进行10次独立随机实验。3种算法的参数如表 6~8所示,为了保证算法比较的公平性,它们的迭代次数和种群规模相同,PSO和ω-PSO算法的学习因子、惯性权重按照文献[20]的推荐值来选择,该文献详细论述了选择过程,本文不再重复。实验结果如表 9~11所示,其中BB×AA×K表示该问题规模为BB个仓门、AA个货车、K种货物,其中O=P=BB/2,M=N=AA/2。
| 表 6 GA参数 Tab. 6 The parameters of GA |
| 表 7 PSO参数 Tab. 7 The parameters of PSO |
| 表 8 ω-PSO参数 Tab. 8 The parameters of ω-PSO |
| 表 9 小规模问题的3种算法结果 Tab. 9 Results of GA, PSO and ω-PSO of instances with small scales |
| 表 10 中等规模问题的3种算法结果 Tab. 10 Results of GA, PSO and ω-PSO of instances with middle scales |
| 表 11 大规模问题的3种算法结果 Tab. 11 Results of GA, PSO and ω-PSO of instances with large scales |
从表 9~11可以看出,对于小规模算例,改进粒子群算法在求解质量上与标准粒子群算法和遗传算法相差不大,都可以找到最优解,在求解时间上改进粒子群算法和标准粒子群算法基本一致,但优于遗传算法;对于中等规模算例,改进粒子群算法在求解质量上的表现最为突出,在求解时间上的表现要稍逊于标准粒子群算法,但仍然优于遗传算法;对于大规模问题,改进粒子群算法的表现基本与中等规模一致。为了更加直观地比较改进粒子群算法相对于标准粒子群算法在求解质量和时间上的改善,本文定义了两者之间的求解质量Gap1和求解时间Gap2,计算公式如下:
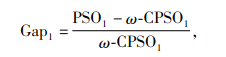
|
(26) |
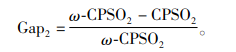
|
(27) |
式中,PSO1和PSO2表示标准粒子群算法的平均完工时间和平均求解时间,ω-CPSO1和ω-CPSO2表示改进粒子群算法的平均完工时间和平均求解时间。中等规模和大规模问题下相对Gap值如表 12所示,可以看出,改进粒子群算法与标准粒子群算法相比,求解质量上的优势相对于求解时间上的劣势要突出很多。
| 表 12 标准粒子群算法与改进粒子群算法相对Gap Tab. 12 The relative gap between PSO and ω-PSO |
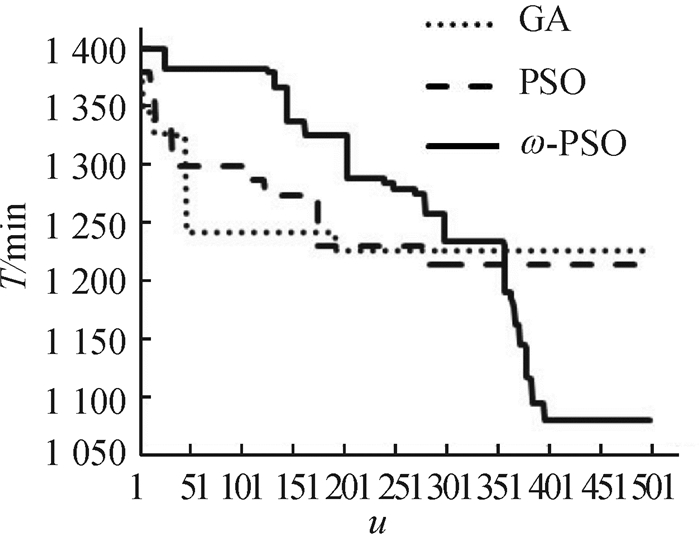
为了更加清晰地表现3种算法的性能差异,本文选用大规模问题(仓门总数24,货车总数140,货物种类数700)绘制它们的进化曲线图,如图 6所示,纵坐标表示完工时间,横坐标表示迭代次数。由图 6可知,标准粒子群算法和遗传算法都较早陷入了局部最优,而改进粒子群算法的迭代曲线是不断下降的,因此,改进粒子群算法拥有较强的跳出局部最优的能力,且在进化初期更趋向于全局搜索,与预期目标一致。
|
图 6 3种算法进化曲线图 Fig. 6 The evolution curve of GA, PSO and ω-PSO |
在越库调度过程中,将货物的实际装卸顺序要求考虑在内,使得车辆调度研究更加贴近现实,对实际运作具有十分重要的指导意义。本文研究了一种考虑货物装卸顺序要求的越库仓门分配和货车排序优化问题,建立以最小化完工时间为目标的整数线性规划模型,并提出改进粒子群算法进行求解。通过数值实验表明所提算法与标准粒子群算法和遗传算法相比,在求解质量上有明显优势,尤其在仓门数、货车数和货物种类数较多的情况下,优势更加显著。在以后的研究中,将进一步考虑货车以中断和非中断方式停靠的越库仓门分配和车辆排序优化问题。
| [1] |
STALK G, EVANS P, SHULMAN L E. Competing on capabilities: the new role of corporate strategy[J].
Harvard Business Review, 1992, 70(2): 57-69.
|
| [2] |
FORGER G. UPS starts world's premiere cross-docking operation[J].
Modern Material Handling, 1995, 11(1): 36-38.
|
| [3] |
CE W. Cross docking: concepts demand choice[J].
Material Handling Engineering, 1998, 53(7): 44-49.
|
| [4] |
凤伟. 越库:未来仓库管理的主流[J].
科技资讯, 2008, 31(1): 167.
FENG W. Cross-docking system: the main technology of future warehouse management[J]. Science & Technology Information, 2008, 31(1): 167. |
| [5] |
CHEN F, LEE C Y. Minimizing the makespan in a two-machine cross-docking flow shop problem[J].
European Journal of Operational Research, 2009, 193(1): 59-72.
DOI: 10.1016/j.ejor.2007.10.051. |
| [6] |
马东彦, 陈峰. 以总全完工时间为目标的两台机越库排序的动态规划算法[J].
上海交通大学学报, 2007, 41(5): 852-856.
MA D Y, Chen F. Dynamic programming algorithm on two machines cross docking scheduling with total weighted completion time[J]. Journal of Shanghai Jiaotong University, 2007, 41(5): 852-856. |
| [7] |
陈杰, 陈峰. 非对称不确定性越库调度算法[J].
上海交通大学学报, 2010, 44(9): 1302-1306.
CHEN J, CHEN F. Algorithm on cross docking scheduling in asymmetrically uncertain environment[J]. Journal of Shanghai Jiaotong University, 2010, 44(9): 1302-1306. |
| [8] |
YU W, EGBELU P J. Scheduling of inbound and outbound trucks in cross docking systems with temporary storage[J].
European Journal of Operational Research, 2008, 184(1): 377-396.
DOI: 10.1016/j.ejor.2006.10.047. |
| [9] |
BOLOORI Arabani A R, FATEMI Ghomi S M T, ZANDIEH M. Meta-heuristics implementation for scheduling of trucks in a cross-docking system with temporary storage[J].
Expert Systems with Applications, 2011, 38(1): 1964-1979.
|
| [10] |
LIAO T W, EGBELUA P G, CHANG P C. Two hybrid differential evolution algorithms for optimal inbound and outbound truck sequencing in cross docking operations[J].
Applied Soft Computing, 2012, 12(1): 3683-3697.
|
| [11] |
BOLOORI Arabani A R, ZANDIEH M, FATEMI Ghomi S M T. A cross-docking scheduling problem with sub-population multi-objective algorithms[J].
International Journal of Advanced Manufacturing Technology, 2012, 58(1): 741-761.
|
| [12] |
TARHINI A, MAKKI J, CHAMSEDDING M M J. Scatter search algorithm for the cross-dock door assignment problem[C/OL]. (2014-04-13). http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6820575.
|
| [13] |
LIAO T W, EGBELUA P G, CHANG P C. Simultaneous dock assignment and sequencing of inbound trucks under a fixed outbound truck schedule in multi-door cross docking operations[J].
Int. J. Production Economics, 2013, 141(1): 212-229.
DOI: 10.1016/j.ijpe.2012.03.037. |
| [14] |
MIAO Z W, LIM A, MA H. Truck dock assignment problem with operational time constraint within crossdocks[J].
European Journal of Operational Research, 2009, 192(1): 105-115.
DOI: 10.1016/j.ejor.2007.09.031. |
| [15] |
MIAO Z W, CAI S, XU D. Applying an adaptive tabu search algorithm to optimize truck-dock assignment in the crossdock management system[J].
Expert Systems with Applications, 2014, 41(1): 16-22.
DOI: 10.1016/j.eswa.2013.07.007. |
| [16] |
KUO Y. Optimizing truck sequencing and truck dock assignment in a cross docking system[J].
Expert Systems with Applications, 2013, 40(14): 5532-5547.
DOI: 10.1016/j.eswa.2013.04.019. |
| [17] |
LEE K, KIM B S, JOO C M. Genetic algorithms for door-assigning and sequencing of trucks at distribution centers for the improvement of operational performance[J].
Expert Systems with Applications, 2012, 39(1): 12975-12973.
|
| [18] |
余小兵. 基于改进粒子群算法的多目标应急物资调度[J].
工业工程, 2014, 17(3): 18-21.
YU X B. Multi-objective emergency supplies scheduling based on improved particle swarm optimization[J]. Industrial Engineering Journal, 2014, 17(3): 18-21. |
| [19] |
纪震, 廖惠连, 吴青华.粒子群算法及应用[M].北京:科学出版社, 2009:21.
|
| [20] |
EBERHART R, SHI Y. Comparing inertia weights and constriction factors in particle swarm optimization[C/OL]. (2000-07-16). http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=870279.
|
 2016, Vol. 19
2016, Vol. 19