混流装配线排序问题已成为学者研究的热点。文献[1]以最小化超载时间与空闲时间的费用为目标,采用免疫粒子群优化算法求解,但该研究没有考虑其他影响装配线效率的因素; 文献[2]建立了以最小化超载时间、最小化调整时间和最小化产品变化率为目标的优化模型,利用混合群优化算法求解,文献[3]则对文献[2]中的目标通过遗传算法进行求解,这两种算法对问题的求解都取得了一定的效果,但未对这三个目标的冲突和竞争进行分析; 文献[4]同时考虑零部件消耗速率均匀化和最小生产循环周期最短两个目标,采用加权和的方法把多目标优化问题转化为单目标优化问题,设计了一种基于遗传算法和模拟退火算法的混合求解方法; 文献[5]设计了改进的离散群优化算法求解以最小超载、空闲和调整时间的费用为目标的多目标优化模型; 文献[6]采用加权和的方法将以最小化调整时间和最小化超载时间与空闲时间为目标的优化问题转化为单目标问题,提出了一种混合人工蜂群算法; 文献[7]建立了以最小化工作站闲置/超载总成本、产品变化率和产品切换总时间为目标的混流装配线排序多目标优化模型,并设计了一种改进多目标猫群优化算法进行求解; 文献[8]同时考虑零部件消耗均匀化和最小生产循环周期最短两个优化目标,提出了一种多目标遗传算法,该研究没有考虑缓冲区容量的约束,而且只是将多目标优化的结果与标准遗传算法单目标优化结果进行了比较; 其他有关混流装配线排序问题的研究可参考综述性文献[9-10]。尽管装配线排序问题研究较多,但是对缓冲区容量约束下,同时考虑关键部件消耗均匀化和完工时间最小目标的混流装配线排序问题研究甚少,因此,本文设计新的多目标优化算法对该问题进行求解。
1 数学模型 1.1 关键部件消耗均匀化
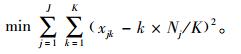
|
(1) |

|
(2) |
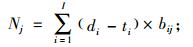
|
(3) |
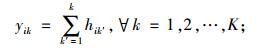
|
(4) |
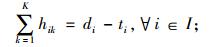
|
(5) |
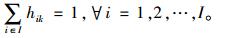
|
(6) |
其中,xjk为装配前k个产品消耗部件j的数量,Nj为装配完所有产品消耗部件j的数量,di为产品i的订单需求数量,ti是产品i的多余库存量,如果产品i被安排在第k个位置进行装配,则hik为1,否则hik为0,yik表示前k个产品中产品i的数量,bij为一件产品i需要部件j的数量。如果部件j的消耗是均匀的,那么,当完成第k件产品后,部件j消耗的数量应该等于(k×Nj/K)。优化目标(式(1))就是尽可能使得当完成第k件产品后,部件j实际消耗的数量xjk尽可能地与(k×Nj/K)接近。
1.2 最长完工时间最小化
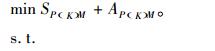
|
(7) |
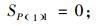
|
(8) |
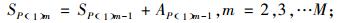
|
(9) |
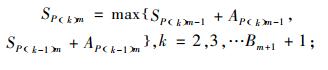
|
(10) |
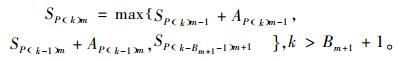
|
(11) |
其中,SP(K)M和AP(K)M分别为最后一件产品P(K)在最后一个工位M上开始装配的时间和所需的装配时间,Bm为工位m和工位m-1之间的缓冲区容量。
2 多目标遗传算法(MOGA) 2.1 算法步骤S1:产生初始种群P(0),种群规模为Mg,令进化代数g=0。
S2:对P(g)中的个体进行Pareto排序,将排序级别为1的个体加入非支配解集Gset中,非支配解集规模为Ng,初始为空,当Gset中个体的数量超过Ng时,要对其进行修剪。
S3:计算P(g)中各个体的小生境计数。
S4:计算P(g)中各个体的适应度值。
S5:进行选择、混合交叉和启发式变异操作。
S6:保留精英个体。
S7: g=g+1,如果g>G,则输出Gset中所有的非支配解; 否则,转S2。
2.2 关键步骤的实现1) 编码:采用整数编码的方式,每种产品用一个唯一的整数代替。
2) 产生初始种群。
S1:采用NEH方法[11]产生1个临时装配序列,其余(Mg-1)个临时装配序列随机产生。
S2:如果产品的多余库存量多于临时序列中该产品的计划数量,则删除所有该产品,否则,从前往后在临时装配序列中删除与多余库存量相同数量的该产品,则剩下的各产品型号的组合即为实际的装配序列。
3) 帕累托分级。
S1:令级数r=1。
S2:任选候选个体xc,如果xc不被P(g)中其他所有个体支配,则令其级数ran(xc)=r。重复此步骤,直到P(g)中个体都被选作候选个体为止。
S3:删除所有级数为r的个体。
S4:如果P(g)中仍有尚未确定级数的个体,则令r=r+1,转S2。
4) 修剪:当Gset的规模超过设定值Ng时,则计算个体的小生境计数,从Gset中删除具有最大小生境计数的个体,如果多个个体的小生境计数相同时,则随机删除一个,重复此步骤,直至Gset的规模等于设定值Ng。
5) 小生境计数。
S1:按下式确定个体之间的距离
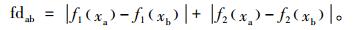
|
(12) |
其中,f1(xa)、f2(xa)、f1(xb)、f2(xb)分别是个体xa和xb的目标函数值。
S2:按下式计算共享函数值
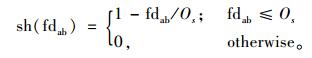
|
(13) |
其中,Os是共享参数。
S3:按下式计算小生境计数
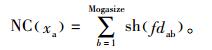
|
(14) |
6) 适应度:因为种群中个体的帕累托级数值越小,则该个体的质量越好,小生境计数越小,则种群中个体的分布性越好,所以为了使具有较小帕累托级数值和较小小生境计数的个体获得较高的适应度,按下式计算个体适应度fit(xa):
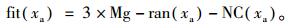
|
(15) |
7) 选择。
S1:按照适应度值由高到低的顺序,选择Mg×Ps个优良个体直接加入下一代种群,比例值Ps事先设定。
S2:对于种群中每一个未被选中的个体,采用随机的方式产生一个新个体,如果新个体支配该未被选中的个体,则将新个体加入下一代种群,如果在连续10次循环中仍不能找到该支配解,则也将该未被选中的个体直接加入下一代种群。
8) 混合交叉。
对于每一对按照交叉概率Pc选择的父本个体,随机从LOX,PMX和modOX 3种交叉算子[12]中任选一种进行交叉操作,然后根据个体适应度值由高到低的顺序从两个子代个体和两个父代个体中选择两个最优个体代替种群中的2个父本个体。
9) 启发式变异。
S1:在每一个根据变异概率Pm选择的进行变异操作的个体中任选三个基因。
S2:任意交换3个基因的位置,产生6个邻域个体。
S3:从6个邻域个体中选择适应度值最大的个体作为变异结果。
10)精英策略。
S1:根据适应度值对临时种群Pt(g)和Gset中的个体进行降序排列。
S2:选择Gset中最优的Q0个个体替换Pt(g)中最差的Q0个个体。
3 多目标模拟退火算法(MOSA) 3.1 算法步骤S1:随机产生初始种群Sset, 种群规模为Ms,令循环次数t=0,初始温度Te=T0。
S2:从Sset中随机选取一个当前个体。
S3:如果终止条件(Te < Ts或t>tmax)满足,则对Sset中的个体进行Pareto分级,输出所有级别为1的非支配个体,否则执行以下步骤。
S4:循环以下步骤Ni次。
1) 采用INV[12]算子,由当前个体产生一个候选个体。
2) 如果候选个体与Sset中的所有个体都不互相被支配,则将该候选个体作为新的当前个体,同时将该候选个体加入Sset中,并对Sset进行修剪; 否则,如果该候选个体支配Sset中的一个或多个个体,则用该候选个体替换Sset中第一个找到的被支配个体,同时将该候选个体作为新的当前个体; 否则,如果Metropolis准则是“真”,则用该候选个体作为新的当前个体。
S5:Te=Te×Cr,t=t+1,转S3。
3.2 修剪当Sset的规模超过设定值Ns时,计算每个个体的小生境计数,删除具有最大小生境计数的个体,如果多个个体的小生境计数相同时,则随机删除一个,重复此过程,直至Sset中规模等于设定值Ns。
3.3 Metropolis准则Metropolis标准表明被支配个体被接受的概率,该概率值按下式计算:
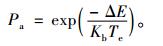
|
(16) |
式中,ΔE是候选个体与Sset中支配它的所有个体间的最小距离,Kb为Boltzman常数。对于被支配的候选个体,首先计算Pa,然后随机产生u(0≤u≤1),如果u < Pa,则Metropolis准则为“真”,否则为“假”。
4 优化结果的比较本文采用了满意度函数的方法用于多目标算法优化结果的比较。非支配解集中的每个个体的满意度按照下式计算。
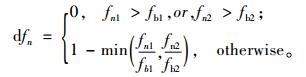
|
(17) |
其中,fn1和fn2分别是个体n的第一个和第二个目标函数值,fb1和fb2分别是非支配解集中第一个目标和第二个目标的最大值。非支配解集的满意度按下式计算,N是非支配解集中个体的总数。
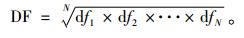
|
(18) |
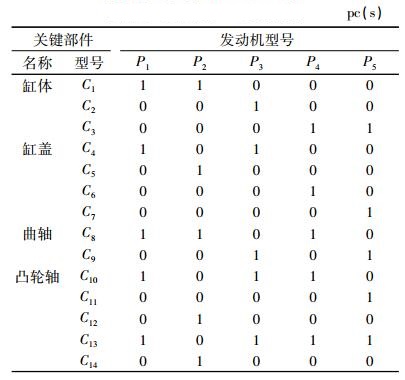
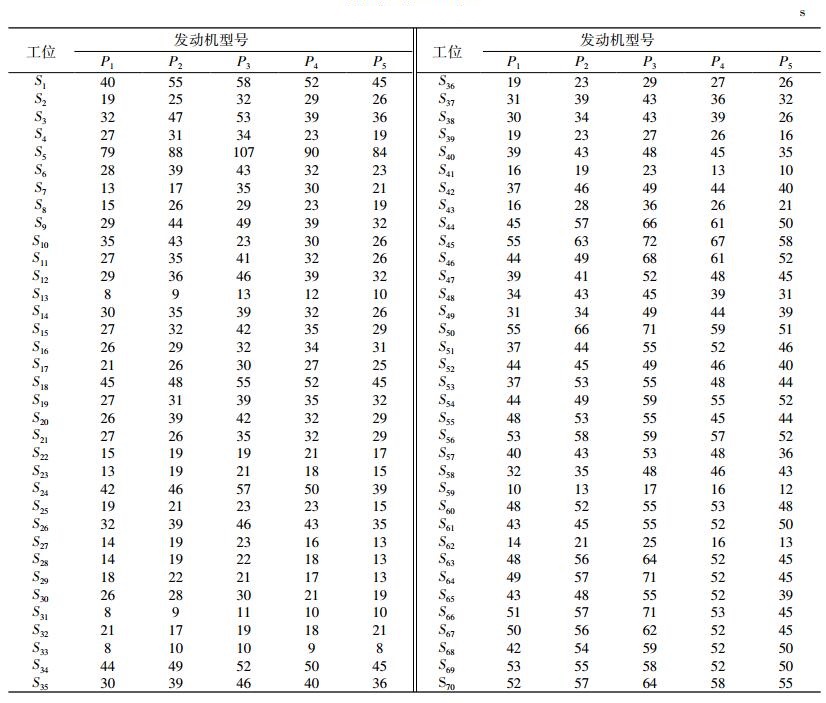
以某汽车制造企业发动机装配线的实际数据验证所设计多目标优化算法的优化性能。该发动机装配线共有70个工位,相邻工位间缓冲区容量分别为:(1,2,1,2,1,1,3,1,2,1,1,1,2,1,2,1,1,3,1,2,1,1,1,2,1,2,1,1,3,1,2,1,1,1,2,1,2,1,1,3,1,2,1,1,1,2,1,2,1,1,3,1,2,1,1,1,2,1,2,1,1,3,1,2,1,1,2,1,2),可混流生产5种型号的发动机,每台发动机均需使用4种关键部件,即缸体、缸盖、曲轴和凸轮轴,每种关键部件有多种型号。发动机订单需求量分别为(60,70,40,80,40),5种发动机的多余库存分别为10台,产品-部件矩阵如表 1所示,作业时间如表 2所示。从订单需求量中减去每种发动机计划期初多余库存量,可以看出,最小生产循环为(5,6,3,7,3),重复10次生产即可满足订单需求。
| 表 1 产品-部件消耗矩阵 Tab. 1 Product-part matrix |
| 表 2 作业时间 Tab. 2 Process time |
算法采用Matlab编程实现,在PC机(Pentium (R) 4, CPU 2.80 GHz, 2G)上运行,针对不同的算法参数组合经过大量的计算实验,选择的MOGA算法参数:Mg=50,G=50,Pc=0.85,Pm=0.20,Ng=10,Os=20,Q0=2,Ps=0.20;MOSA算法参数:T0=50,Ts=1,Co=0.95,kmax=50,Ni=30,Ms=50,Ns=10,Os=20,Kb=0.005。
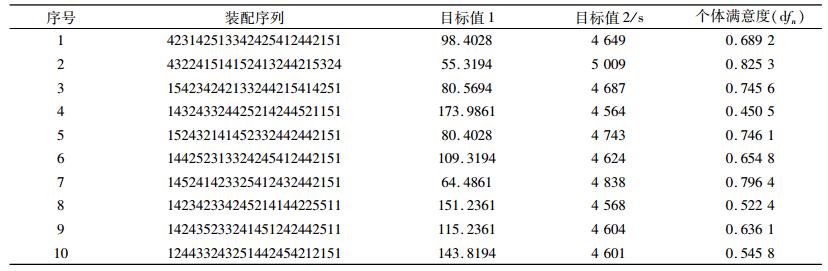
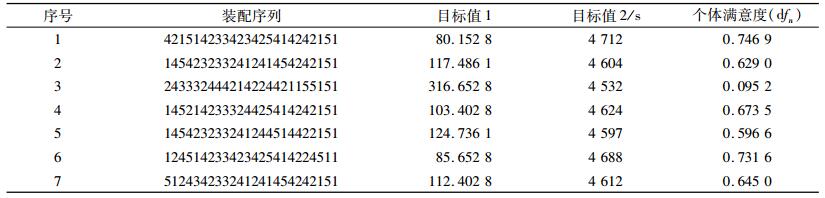
多目标遗传算法的优化结果和个体满意度如表 3所示,计算时间642 s,多目标模拟退火算法的优化结果和个体满意度如表 4所示,计算时间723 s。
| 表 3 MOGA算法优化结果 Tab. 3 Optimization results of MOGA |
| 表 4 MOSA算法优化结果 Tab. 4 Optimization results of MOSA |
从表 3和表 4可以看出:1) MOGA找到的非支配解的个数多于MOSA找到的非支配解的个数; 2)根据公式(18)计算两种算法优化所得的非支配解集的满意度值,结果分别为0.6501和0.5059,说明MOGA优化结果的满意度要高于MOSA优化结果的满意度; 3) MOGA的CPU耗时要短于MOSA,说明MOGA的优化效率更高。
6 结论1) 以关键部件消耗均匀化和最大完工时间最小化为目标,建立了缓冲区容量约束下发动机混流装配排序问题数学模型,设计了两种多目标优化算法用于问题的求解。
2) 结合实例,比较了两种算法的优化结果,发现在解的数量、满意度和计算效率3个方面,多目标遗传算法均具有优势。
| [1] |
郑永前, 王永生. 免疫粒子群算法在混流装配线排序中的应用[J].
工业工程与管理, 2011, 16(4): 16-20.
ZHENG Yongqian, WANG Yongsheng. An immunity particle swarm sequencing algorithm for mixed-model assembly lines[J]. Industrial Engineering and Management, 2011, 16(4): 16-20. |
| [2] |
HYUN C J, KIM Y, KIM Y K. A genetic algorithm for multiple objective sequencing problems in mixed model assembly lines[J].
Computers & Operations Research, 1998, 25(7/8): 675-690.
|
| [3] |
刘炜琪, 刘琼, 张超勇, 等. 基于混合粒子群算法求解多目标混流装配线排序[J].
计算机集成制造系统, 2011, 17(12): 2590-2598.
LIU Weiqi, LIU Qiong, ZHANG Chaoyong, et al. Hybrid particle swarm optimization for multi-objective sequencing problem in mixed model assembly lines[J]. Computer Integrated Manufacturing Systems, 2011, 17(12): 2590-2598. |
| [4] |
苏平, 于兆勤. 基于混合遗传算法的混合装配线排序问题研究[J].
计算机集成制造系统, 2008, 14(5): 1001-1007.
SU Ping, YU Zhaoqin. Hybrid genetic algorithms for sequencing problems in mixed model assembly lines[J]. Computer Integrated Manufacturing Systems, 2008, 14(5): 1001-1007. |
| [5] |
董巧英, 阚树林, 桂元坤, 等. 基于改进离散微粒群优化算法的混流装配线多目标排序[J].
系统仿真学报, 2009, 21(22): 7103-7108.
DONG Qiaoying, KAN Shulin, GUI Yuankun, et al. Mixed model assembly line multi-objective sequencing based on modified discrete particle swarm optimization algorithm[J]. Journal of System Simulation, 2009, 21(22): 7103-7108. |
| [6] |
鲁建厦, 翁耀炜, 李修琳, 等. 混合人工蜂群算法在混流装配线排序中的应用[J].
计算机集成制造系统, 2014, 20(1): 121-127.
LU Jiansha, WENG Yaowei, LI Xiulin, et al. Application of hybrid artificial bee colony algorithm in mixed assembly lines sequencing[J]. Computer Integrated Manufacturing Systems, 2014, 20(1): 121-127. |
| [7] |
刘琼, 范正伟, 张超勇, 等. 基于多目标猫群算法的混流装配线排序问题[J].
计算机集成制造系统, 2014, 20(2): 333-342.
LIU Qiong, FAN Zhengwei, ZHANG Chaoyong, et al. Mixed model assembly line sequencing problem based on multi-objective cat swarm optimization[J]. Computer Integrated Manufacturing Systems, 2014, 20(2): 333-342. |
| [8] |
YU J F, YIN Y H, CHEN Z N. Scheduling of an assembly line with a multi-objective genetic algorithm[J].
International Journal of Advanced Manufacturing Technology, 2006, 28(5): 551-555.
|
| [9] |
BOYSEN N, FLIEDNER M, SCHOLL A. Sequencing mixed-model assembly lines: survey, classification and model critique[J].
European Journal of Operational Research, 2009, 192(2): 349-373.
DOI: 10.1016/j.ejor.2007.09.013. |
| [10] |
JIMENEZ P. Survey on assembly sequencing: a combinatorial and geometrical perspective[J].
Journal of Intelligent Manufacturing, 2013, 24(2): 235-250.
DOI: 10.1007/s10845-011-0578-5. |
| [11] |
WANG L, ZHANG L, ZHENG D Z. An effective hybrid genetic algorithm for flow shop scheduling with limited buffers[J].
Computers & Operations Research, 2006, 33(10): 2960-2971.
|
| [12] |
WANG L, ZHENG D Z. An effective hybrid heuristic for flow shop scheduling[J].
International Journal of Advanced Manufacturing Technology, 2003, 21(1): 38-44.
DOI: 10.1007/s001700300005. |
 2016, Vol. 19
2016, Vol. 19