在当今激烈的竞争环境下,中国企业遭受了前所未有的质量风暴。中国制造业的危机的原因之一是由于中国企业较少将先进的质量工具应用在产品设计阶段,设计能力的缺失限制了企业自称研发能力的提高,而先进质量管理理念的缺乏,更是使得这种危机日益加重。质量管理的重要理念就是产品质量首先要设计其次才能制造。产品设计是获得高质量产品的首要保证。六西格玛管理就是时下最为先进的质量管理理念,其在中国的推广也最为迅速,我国政府和许多企业都积极地将其引入进来。六西格玛管理的DMICA流程中I(improvement)阶段的主要工具就是试验设计(design of experiments,DOE)。试验设计旨在通过调整系统中的输入变量以分析输入变量与输出响应之间的关系,并使输出响应达到最优值。系统中只有一个输出响应的问题成为单响应优化问题,通过回归方法以及一般的优化方法就能实现。然而,随着工业技术的发展,产品(过程)越来越复杂,顾客需求越来越具有多样性,加之对系统设计问题研究的深入,我们常常遇到通过某种函数关系要比通过一元变量,甚至多元变量能更充分的描述质量特性[1]。这种描述过程(或产品)质量特性的函数关系成为轮廓(profile)[2],利用试验设计方法对质量特性为轮廓的输出响应进行优化,是目前质量工程领域的研究热点。从系统设计角度来看,质量特性为轮廓的输出响应问题我们可以称为函数响应系统。输出响应q不是一个特定的值,而是关于某个变量q≤p的曲线函数,其输出是一条曲线,称为“profile”或“shape”,通过对每条曲线在每个观测点上的值的研究来描述系统的性能[3]。输出的profile假设可以通过可控因子进行调整,其还有可能受噪声的影响,但是本文忽略噪声的影响。函数响应系统问题和田口的信号响应系统[3]或者动态稳健设计问题[4-6]相似,Wu和Joseph[7]称为多目标系统。在信号响应系统问题研究中,Yj被称为信号因子,且j水平很少,其试验的目的是通过调整信号因子水平来调节响应值。动态响应系统的稳健参数设计就是通过这种调整,使得Zk=ak1Y1+ak2Y2+…akpYp=A′kY在噪声的影响下有最小的波动。而函数响应系统的试验设计,虽然试验数据和动态响应系统试验有着相同的结构,但是我们的目的是获得Z=A′Y和Y=(Y1, Y2, …, YP)′, 的理想关系。每一轮试验都会得到一个完整的profile,试验结果profile尽可能地接近目标profile,这个profile由样本函数在S的不同点上的观测值构成,在空间统计学中,将Ak=(ak1, ak2, …, akp)′这种点定义为locations,与其相似的领域是生物统计学[8]中的纵向分析[9-11](longitudinal analysis),其响应值是关于时间的函数。许多作者对profile研究大多停留在产品的控制阶段,被称为“profile monitoring”[12-14]。而在试验设计阶段的相关研究很少,Nair[15]曾提出了基于频率域函数响应系统的建模方法来获得稳健性。本文就是在应用试验设计方法基础上,将profile看成由多个观测点组成,每个观测点看成一个独立的响应,将函数响应问题转化为多响应问题,提出了基于主成分分析法的双响应曲面模型和满意度函数相结合的profile优化方法。
1 函数响应优化方法的综述 1.1 主成分分析法主成分分析,就是利用降维的思想,将多个变量转化为少数几个主成分的统计分析方法。其最早是由Pearson[16]提出后经Hotelling[17]进一步发展。利用主成分分析法将P个输出响应(需提前对数据进行标准化以消除量纲的影响)转化为q(q≤p)个无关的主成分,并取特征值大于1的主成分作为优化指标。
用Yj表示第j个输出响应标准化后的数据,可以得到
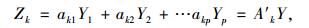
|
(1) |
用矩阵表示为
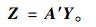
|
(2) |
其中,Y=(Y1, Y2, …, YP)′, Ak=(ak1, ak2, …, akp)′,A=(A1, A2, …, Aq),Z=(Z1, Z2, …, Zq)′,Zk表示第k个主成分,k=1, 2, …, q。第k个主成分的系数ak1, ak2, …, akp是Y的协方差矩阵的第k个特征值所对应的特征向量的元素,满足ak12, ak22, …, akp2=1。
Liao[6]曾指出此方法的两个缺陷就是:1)当特征值大于1主成分不止一个时,仍为多响应问题; 2)舍弃特征值小于1的主成分会导致部分信息的缺失。鉴于此,Liao[18]又提出了一种加权主成分分析法,将每个主成分的方差贡献率作为权重系数,将所有主成分的综合得分做为最终的多响应绩效指标。为解决上述问题,Liao提出了一种基于加权主成分分析的多响应优化方法,选取每个主成分的方差贡献率作为权重系数,以所有主成分的加权和做为最终的多响应绩效指标。主成分的方差贡献率表示为
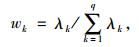
|
(3) |
其中,wk为第k个主成分的方差贡献率,λk为Y的协方差矩阵的第k个特征值。方差贡献率为每个主成分所解释的方差占总方差的比例,表示该主成分对总方差的影响及其相对重要程度,也反映了主成分的信息含量值,保证信息的完整性。所有主成分的加权和即多响应的绩效指标为
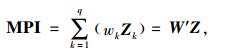
|
(4) |
其中,W=(w1, w2, …wq) ′。
主成分分析法多是应用在多响应优化中,本文将主成分分析法应用到函数响应及Profile的优化中,将每个观测点所对应的观测点看成独立的响应,将Profile优化转化为多响应的优化问题,通过加权主成分分析法对多个响应赋予合理的系数,最终将多响应问题转化为单响应的优化问题,并解释原问题的全部方差,保证信息的完整性。但是此方法的最大缺点就是其优化过程只考虑了响应的均值而没有考虑响应方差的优化,缺乏稳健性。本文就是基于此将双响应曲面法与其结合,解决这一问题。
1.2 满意度函数法满意度函数法是一种简便易行、应用广泛的多响应输出的优化方法。此法最早由Harrington提出来,后来经Derringer[19]等加以改进,使其更加科学与适用。该方法主要思路是将响应值yi转化为满意度函数di,di∈[0, 1]。响应接近目标值,di无限趋近1,响应偏离目标值,di趋近于0或等于0。单个满意度函数为式子(5)。其中,di为第i个响应的个体满意度函数;Li,Ui和Ti分别为第i个响应的下界、上界和目标值;指数si和ti反映了目标值在多大程度上必须被满足。它决定着满意度函数的形状。
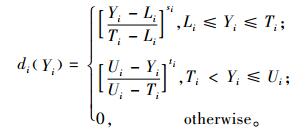
|
(5) |
对于望大型响应,个体满意度函数为:

|
(6) |
对于望小型响应,个体满意度函数为:

|
(7) |
双响应曲面法最早由Myers和Carter[20]提出,弥补波动较大时单响应模型失效情况。随后Vining和Myers[21]对此法进一步改进并扩大到了多响应优化中。双响应曲面法通过同时优化响应的均值和标准差,在保证响应均值尽量接近目标值前提下,使响应的波动尽量最小。假定共有k个可控变量,分别为x1, x2, …xk,则
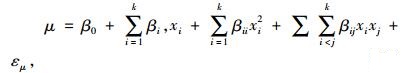
|
(8) |
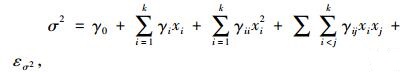
|
(9) |
其中,μ为响应均值,σ为响应标准差,β和γ是模型系数,ε为随机误差。关于双响应曲面优化方法主要有以下几种。
1) Vining和Myers[22]为代表的约束优化法。约束优化就是以均值作为约束条件,标准差为目标函数,通过最小化标准差以达到优化的目的,以望目型为例,假设响应目标值为T,其约束优化问题如下表示:
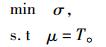
|
(10) |
2) 均方误差法。
此法由Lin和Tu[23]提出,其形式为
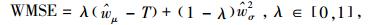
|
(11) |
以均值的偏差来换取方差的极大程度减小。权重λ可根据实际情况选取。最小化WMSE所得到一组可控变量组合即为该问题的最优解。
3) 拉格朗日乘子法。
此法是由Mayer提出的。他将两个响应进行主次区分。双响应优化就将两个响应做主次区分并将次响应作为约束条件,对主响应进行最大或最小处理[24]。具体形式为

|
(12) |
令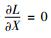
双响应曲面法是单响应优化最常用的方法,后来Quesada[25]将双响应曲面方法扩展至多响应问题的优化。其算法如下:
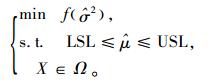
|
(13) |
其中,Ω为可控因子的可行域; 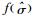
本文所提方法具体步骤如下。
1) 拟合各个观测点的响应均值和方差回归方程。假设共有s个观测点,其对应的观测值为Y(1), Y(2), Y(3), …Y(s),k个输入变量,进行了n次试验,并重复测量。拟合得到第q个观测点响应的均值与标准差的回归方程为:
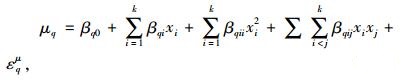
|
(14) |
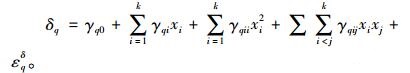
|
(15) |
其中,μq和σq表示第q个观测点所对应的响应值的均值和标准差,βij与γij是模型系数,εij为随机误差。
2) 然后利用式(5)~(7)求得各个观测点均值和方差的满意度函数值d(μqj)和d(σqj)。
3) 利用式(1)对均值和满意度值进行主成分分析。
均值第m个主成分值为
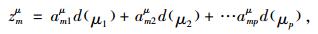
|
(16) |
am1μ, am2μ, …ampμ为第m个主成分的系数。
方差的第m个主成分值为

|
(17) |
an1μ, an2μ, …anpμ为第n个主成分的系数。
4) 计算各响应系数和方差满意函数值的主成分综合得分为:
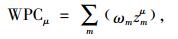
|
(18) |
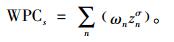
|
(19) |
其中权重ω即为主成分的方差贡献率。
5) 利用加权均方误差函数,计算最终的函数响应绩效指标OPI:
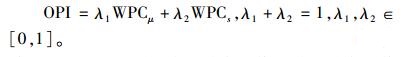
|
(20) |
其中,权重λi可根据位置满意度值和散度满意度值的相对重要程度,或历史经验及实验者的偏好而定。在本文中,主成分得分越小越好,故OPI越小代表质量水平越高,即优化以OPI望小为目标。
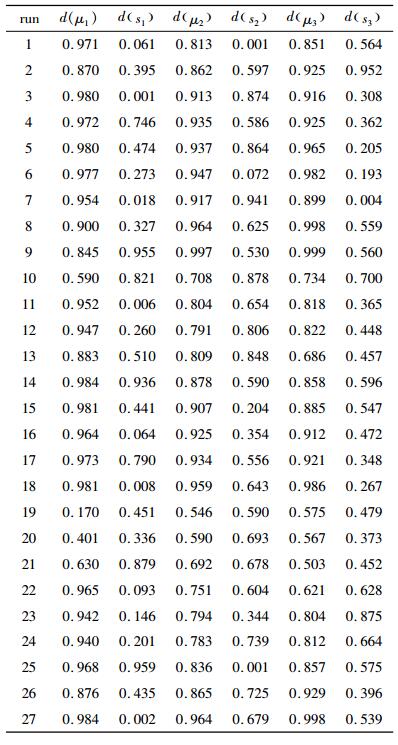
3 应用实例 3.1 数据分析本例数据来自Gohel和Amin[28]对双氯芬酸钠缓释片的缓释率进行的试验研究。双氯芬酸钠缓释片是非甾体抗炎药的主要成分。双氯芬酸钠缓释片的制备可以通过使用不同的包封剂和制备技术来改变药品缓释速率。响应Y表示双氯芬酸钠缓释片的释放比例,其在三个不同的时间点1h,6h,8h上观测值分别为Y(1),Y(2),Y(3),其溶解度的允许范围及其目标值如表 1所示,Y(1),Y(2),Y(3)是望目特性。
| 表 1 响应规格域 Tab. 1 Response specification |
本实验包括3个可控因子如表 2所示。采用中心复合试验(CCD),详细数据参考文献[15]。试验的目的就是研究搅拌速度(x1),氯化钙包封剂浓度(x2),分散介质中液体石蜡的所占百分比(x3)在给定的药品靶释值(如表 1所示)前提下,对缓释药品的影响,确定双氯芬酸钠缓释片的最优因子设置。
| 表 2 可控因子表 Tab. 2 Control factor and their levels |
根据式(14)~(15)拟合得到每个时间点上的响应均值和标准差的最佳回归方程为:
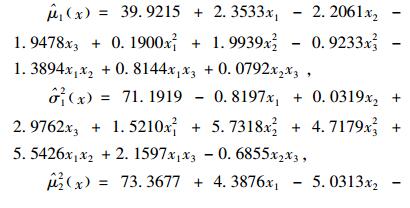
|

|
根据式(5)~(6)利用JMP软件得到各个观测。
点响应的均值和标准差的满意度值如表 3所示。
| 表 3 均值和标准差的满意度值 Tab. 3 The desirability of mean and standard deviation |
利用JMP软件,对3个观测点响应值的均值满意度值进行主成分分析,得到结果如表 4所示。
| 表 4 均值满意度值的主成分分析表 Tab. 4 Principal components analysis for means |
根据式(16)得到相应的主成分函数为:
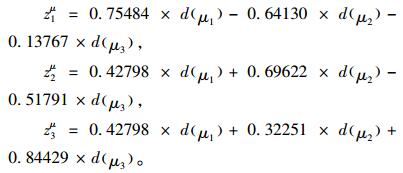
|
根据式(17)得到各响应位置特性值的加权主成分为:
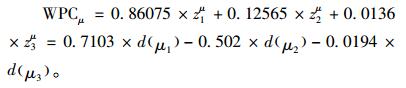
|
根据式子利用JMP软件,得到标准差的渴求函数值与可控变量的拟合回归方程为:
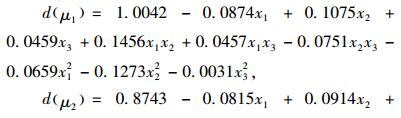
|

|
进而得到:
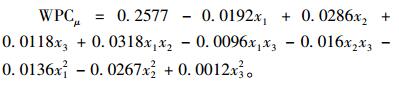
|
同上,对3个观测点响应的标准差满意度值进行主成分分析,可得到如表 5结果。
| 表 5 标准差满意度值的主成分分析表 Tab. 5 Principal components analysis for standard deviation |
根据式(18)同上求出相应方差渴求函数值的主成分函数为:

|
根据式(19)得到各响应标准差特征值的主成分综合得分为:

|
利用JMP软件,得到方差的渴求函数值与可控变量的拟合回归方程为:
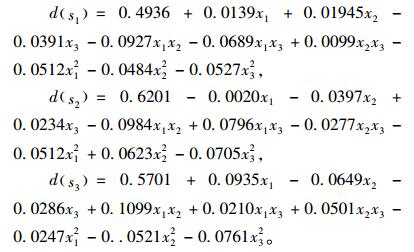
|
进而得到:
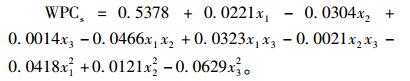
|
根据式(20)最终的绩效指标OPI:
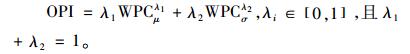
|
令λ1=0.2, λ2=0.8,得
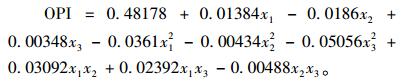
|
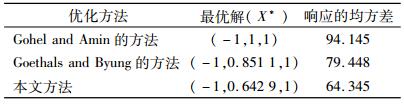
优化结果如表 6所示。本文提出的优化方法,同时考虑均值和标准差,并根据λ取值的不同,决定方差和标准差的重要性。而Goethals的方法用重叠等直线图来确定最优因子水平的设置,这种方法只考虑到响应的均值,没有考虑响应的方差。而Goethals的方法同时考虑响应的均值和标准差,与本文的方法初衷相同,其结果与本文结果具有横向比较的价值。本文令λ1=0.2, λ2=0.8,得到的结果可以使得响应的均方差更小,结果更优。本文利用主成分分析法将原响应转换成一系列不相关的部分,因而减少了函数响应问题中设计参数优化冲突的问题。
| 表 6 优化结果比较 Tab. 6 the comparison of optimization results |
本文目的在于如何利用试验设计的方法对函数响应进行优化。这种优化方法思路就是将profile每个观测点看成一个独立的响应,将profile问题转化为多响应问题。基于此优化思路本文提出了一种基于双曲面方法的主成分分析和渴求函数相结合的profile优化方法。首先通过主成分分析法对函数响应问题进行降维,考虑观测点之间的相关性。然后通过将双响应曲面模型和满意度函数进行结合,将具有函数响应性质问题转化为多响应问题,并整合成单一指标来决定最佳因子水平组合。实例分析的结果显示,本文提出的方法切实可行有效,可操作性强,简单实用。此方法的不足之处在于,最后的评价指标中关于权重系数λi没有给出有效的确定方法。对于profile,我们是选取了其中个别具有代表性的点作为研究对象,这种方法不能很好地描述函数响应的关系,具有一定的局限性。
| [1] |
MONTGOMERY D C. Design and Analysis of Experiments[M]. John Wiley & Sons, 2009.
|
| [2] |
FOGLIATTO F S. Multiresponse optimization of products with functional quality characteristics[J].
Quality and Reliability Engineering International, 2008, 24(8): 927-939.
DOI: 10.1002/qre.v24:8. |
| [3] |
GELFAND I M, FOMIN S V. Calculus of variations. Englewood Cliffs, NJ: Prentice Hall, 1963.
|
| [4] |
TAGUCHI G. Introduction to Quality Engineering: Designing Quality into Products and Processes[M]. Tokyo: Asian Productivity Organization, 1986.
|
| [5] |
MILLER A. Analysis of parameter design experiments for signal-response systems[J].
Journal of Quality Technology, 2002, 34(2): 139-151.
DOI: 10.1080/00224065.2002.11980141. |
| [6] |
MCCASKEY S D, TSUI K L. Analysis of functional response design experiments[J].
International Journal of Quality Technology, 1997, 35(6): 1561-1574.
|
| [7] |
MILLER A, WU C F J. Parameter design for signal-response systems:a different look at taguchi's dynamic parameter design[J].
Statistical Science, 1996, 11(2): 122-136.
DOI: 10.1214/ss/1038425656. |
| [8] |
WU C F J, HAMADA M. Experiments, Planning, Analysis and Parameter Design Optimization[M]. New York, NY: John Wiley & Sons, 2000.
|
| [9] |
DIGGLE P, HEAGERTY P, LIANG KY, Zeger S. Analysis of Longitudinal Data[M]. Oxford University Press: London, UK, 2013: 5.
|
| [10] |
FAN J, ZANG J T. Two-step estimation of functional linear models with application to longitudinal data[J].
Journal of the Royal Statistical Society, Series B: Statistical Methodology, 2000, 62: 303-322.
DOI: 10.1111/1467-9868.002336. |
| [11] |
FITZMAURICE G M, LAIRD N M, WARE J H. Applied Longitudinal Analysis[M]. Hoboken, NJ: John Wiley & Sons, 2004.
|
| [12] |
KIM K, MAHMOUD MA, WOODALL WH. On the monitoring of linear profiles[J].
Journal of Quality Technology, 2003, 35(3): 317-328.
DOI: 10.1080/00224065.2003.11980225. |
| [13] |
QIU P, ZOU C, WANG Z. Nonparametric profile monitoring by mixed effects modeling[J].
Technometrics, 2010, 52: 265-277.
DOI: 10.1198/TECH.2010.08188. |
| [14] |
NOOROSSANA R, SAGHAEI A, AMIRI A. Statistical Analysis of Profile Monitoring[J]. John Wiley & Sons: Hoboken, NJ, 2011.
|
| [15] |
NAIR V N, TAM W, YE K Q. Analysis of functional responses from robust design studies[J].
Journal of Quality Technology, 2002, 34(4): 355-370.
DOI: 10.1080/00224065.2002.11980169. |
| [16] |
PEARSON K. On lines and planes of closes fit to a systems of points in space[J].
Philosophica Magazine, 1901, 2(11): 559-572.
|
| [17] |
HOTELLING H. Analysis of a complex of statistical variables into principal components[J].
Journal of Educational Psyc-hology, 1933, 24(6): 417-414.
DOI: 10.1037/h0071325. |
| [18] |
LIAO H C. Multi-response optimization using weighted pri- ncipal component[J].
The International Journal of Adva- nced Manufacturing Technology, 2006, 27(7): 720-725.
|
| [19] |
DERRINGER G C, SUICH R. Simultaneous optimization of sev- eral response variables[J].
Journal of Quality Technology, 1980, 12(4): 214-219.
DOI: 10.1080/00224065.1980.11980968. |
| [20] |
MYERS R H, CARTER W H. Response surface techniques for dual response systems[J].
Technometrics, 1973, 15(2): 301-317.
DOI: 10.1080/00401706.1973.10489044. |
| [21] |
VINING G G, MYERS R H. Combining taguchi and response surface philosophies:a dual response approach[J].
Journal of Quality Technology, 1990, 22(1): 38-45.
DOI: 10.1080/00224065.1990.11979204. |
| [22] |
LIND K J, TU W. Dual response surface optimization[J].
Jo- urnal of quality Technology, 1995, 27(1): 34-39.
DOI: 10.1080/00224065.1995.11979556. |
| [23] |
KAREN A F C, NELSON P P. Dual response optimization via direct function minimization[J].
Journal of Quality Tech-nology, 1996, 28(2): 34-38.
|
| [24] |
QUESADA G M, CASTILLO E D, PETERSON J J. A Bayesian app-roach for multiple response surface optimization in the p-resence of noise variables[J].
Journal Applied Statistics, 2004, 31(3): 251-270.
DOI: 10.1080/0266476042000184019. |
| [25] |
HE Zhen, WANG Jing, PARK S H. Robust optimization for m- ultiple responses using response surface methodology[J].
Applied Stochastic Models in Business and Industry, 2010, 26(2): 157-171.
DOI: 10.1002/asmb.v26:2. |
| [26] |
杨方, 高齐圣, 于增顺. 多响应问题的稳健性设计优化[J].
工业工程, 2010, 13(3): 43-46.
YANG Fang, GAO Qiaheng, YU Zengshun. Robust design optimization of multi-response proplems[J]. Industrial Engineering Journal, 2010, 13(3): 43-46. |
| [27] |
GOHEL M, AMIN A. Formulation optimization of controlled release diclofenac Sodium microspheres using factorial d- esign[J].
Journal of controlled release, 1998, 51(2/3): 115-122.
|
| [28] |
GOETHALS P, ARAGON L, CHO B R. Experimenta investigations of estimated response surface function with different mea- sures[J].
International Journal of Experimental Design and P- rocess Optimization, 2009, 1(2/3): 123-163.
DOI: 10.1504/IJEDPO.2009.030316. |
 2016, Vol. 19
2016, Vol. 19