拉式生产理念在生产加工中逐渐普及,面向客户的定制化生产在食品生产加工行业屡见不鲜。不同的原材料,通过流线式(flow-shop)生产线,实现客户的定制化需求。在生产加工过程中,为保证产品的质量,需要尽量保证产品不会太长时间直接暴露在产线环境中。在实际的生产过程中,通过控制在制品(work-in-process,WIP)库存来避免产品长时间直接暴露在产线环境中。另一方面,由于制造工艺的原因,难免会在生产过程中存在一些工作负担比较大的环节(负荷的不均衡)。针对这种类型的生产环境,约束理论(theory of constraints,TOC)提供了较好的管理理念[1]。
TOC强调控制系统的受限资源来获取最大的系统产出。在实际的实施过程中,DBR理论提供了一套行之有效的闭环控制流程。DBR理论认为,一个企业计划与控制的目标是寻求市场需求与企业能力的最优配合,一旦一个被控制的作业(即瓶颈作业)建立了一个动态平衡,其余作业应相继与瓶颈作业同步[2]。DBR理论对生产过程中存在的瓶颈资源环节设置缓冲区,通过对缓冲区的WIP库存控制,在保证整个生产过程延续性的同时控制合理的WIP库存。典型的DBR理论应用过程包括4个固定的环节[3]:1)系统瓶颈的识别; 2)系统缓冲的计算; 3)生产节奏的安排; 4)投料控制。通过缓冲管理(buffer management,BM)机制来实现投料控制,通过控制整个系统的投料时间以及投料数量来实现WIP库存控制[4]。经典的缓冲管理机制将系统的缓冲划分为3个区域[5]:绿色区域,黄色区域,红色区域。具体的管理流程为:当检查时缓冲中的WIP库存位于绿色区域,则不需要投料; 如果检查时缓冲中的WIP库存位于黄色区域,则需要进行一定的投料; 如果缓冲区的WIP库存落入红色区域,则需要进行紧急投料。
DBR理论一经提出即得到了广泛的关注。李爱华等[6]在考虑随机故障的情形下,给出了一套计算瓶颈缓冲大小的数学模型。Wu等[7]讨论了在半导体生产环境中,针对半导体制作工艺的特殊性,引入了回流缓冲的概念。Huang等[8]讨论了通过重排产切入时机的控制,可以有效地改善普通DBR理论的排产系统的短板。杨琴等[9]充分研究在柔性流水车间调度中存在的困难,给出了一套将瓶颈资源调度与非瓶颈资源调度相互协调的调度机制,并给出了相关的动态调度规则,有效地改善了柔性流水车间生产调度的效率。徐云天等[13]提出了一种动态DBR方法。该方法通过综合考虑系统生产速度存在的变动和系统的随机故障,根据订单中每个产品实际抵达缓冲区的时间和理论时间之间的对比关系对缓冲的大小进行调节,在保证系统产出的同时降低系统平均在制品数量。
DBR管理机制在实际的生产运作当中也得到了积极的肯定[10-12]。但是,目前普遍采用的缓冲管理机制是一种静态的管理机制,在这种管理机制中,缓冲区大小一旦确定,后续管理全部针对该缓冲实施。如此处理存在一定的不足:管理的有效性对缓冲计算结果准确性的依赖程度太高,计算结果太大导致WIP库存太多,计算结果太小导致瓶颈饥饿等。
在典型DBR控制流程的基础之上,文献[13]对缓冲区大小的确定提出了一种改良的动态方法,但是该DBR方法中投料机制依然采用传统的方法。本文拟对缓冲区采用了一套动态的管理机制:根据系统的实际运作情况,对缓冲区的安全上下限进行动态的调节,在保证生产准时的前提下,控制缓冲区的WIP库存在合理的范围之内。
1 基于DBR理论的排产系统的建模 1.1 系统描述本文以酒类包装生产为研究对象。在酒类包装生产的过程中存在的5个典型的加工环节,具体如下。
1) 单品包装,操作员将单品进行打包;
2) 包装打码,对每一个单品包装进行单独的赋码,赋予唯一的条码;
3) 打码校验,对前一环节赋到包装上的条码进行校验,如果校验不通过认定赋码失败,将该产品剔除;
4) 产品组箱,将单个产品按照一定的数量规格进行组箱;
5) 产品组盘,将箱规格的产品组合到托盘以便进行入库管理。
整个过程如图 1所示。
|
图 1 酒类包装生产过程 Fig. 1 Wine packaging process figure |
将该过程抽象为Flow-Shop产线,每一个工序对应一个工作站,如图 2所示。产线有m个工作站,所有类型的产品加工过程必须经过所有工作站的处理。对于不同的产品每个工作站理想的加工时间PTim不尽相同。

|
图 2 加工过程示意图 Fig. 2 Wine packaging process diagram |
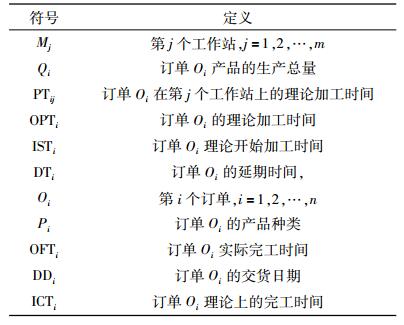
其中变量的定义如表 1所示。
| 表 1 变量定义 Tab. 1 Definition of variables |
如图 2所示,产品Pi到来后分别经过M1到Mm生产加工,各个加工环节的加工时间分别为PTij, j=1, 2…, m,产品从一个加工环节出来直接到下一个加工环节。假设该生产过程中工序Mb为瓶颈资源,对于整个系统而言,除Mb以外的生产环节对系统整体产出的影响远远小于Mb对产出的影响——在Mb上的误工将导致整个系统的产出降低。对于Mb之前的工序,如果停摆,可能导致Mb停工。对于可恢复机器故障,如果在Mb前加入一定规模的缓冲,能够保证停摆工序在恢复前Mb能够保持生产,那么这样的停工对系统的产出是不会产生影响。此即为DBR控制的核心理念。
本文的探讨需要基于一些最基本的假设前提:1)系统可以有多个订单,每个订单只包含一种产品; 2)机械故障只考虑瓶颈资源前的工作站,且所有发生的机械故障都是可恢复的; 3)每个产品在同一时间只能在唯一的一个工作站上进行加工,每个工作站在同一时间只能对最多一个产品进行加工; 4)不考虑不同订单之间工作站的准备时间; 5)每个工作站只能进行一种工序的处理,每种产品必须经过所有的工作站进行加工处理。
1.2 DBR理论建模如前说述,DBR理论包括4个典型的步骤,建模过程具体见下文。
1.2.1 瓶颈资源的确定假设系统中存在唯一的瓶颈资源,并且不考虑瓶颈漂移。在给定的工作时长中,平均负荷最大的工作站即为系统的瓶颈资源[14]。平均负荷通过加工时间占比表示,加工时间占比计算公式为
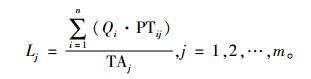
|
(1) |
其中,TAj指在给定时间段中,第j个站台可以工作的总时长。若第b个工作站为瓶颈工序,则有Lb>Lj(其中j=1, 2, …, m,且j≠b)恒成立。
1.2.2 缓冲大小的确定Schragenheim将缓冲分为3大类:瓶颈缓冲,出货缓冲以及装配缓冲[2]。其中,瓶颈缓冲安排在瓶颈工作站前面,用来预防瓶颈饥饿; 出货缓冲安排在瓶颈工作站后面,用来保证订单的准时交货; 装配缓冲也在瓶颈工作站后面,用来保证瓶颈后工序能够及时装配。本文主要考虑在瓶颈工作站前面环节的WIP控制,只对瓶颈缓冲作考虑。对于上一步得出的瓶颈站台Mb,其缓冲大小的计算公式为[15]
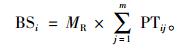
|
(2) |
其中假设产线有m台机器,瓶颈资源位于第b台机器; BSi为产品Pi所要求缓冲的大小; MR为根据经验值设置的乘数。即产品Pi在瓶颈资源前的缓冲为瓶颈资源的前置时间的MR倍。
1.2.3 生产节奏安排生产节奏安排即订单的排序。在以准时制造为主要目标的DBR生产体系中,较为普遍采用的排队原则是基于EDD(最早交货日期优先)原则[16],本文中排队原则具体如下。
1) 首先依据EDD原则进行初步排序;
2) 在交货日期相同的前提下,优先排队延期成本大的订单;
3) 在前面两者都一样的前提下,采用SPT(最短加工时间订单优先)原则排队。
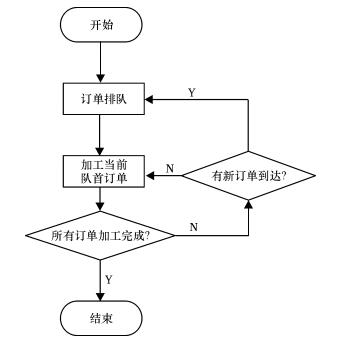
订单一旦开始生产不能被取消(撤单操作),一个订单在生产中不能进行中断并插入其他订单(插单操作)。订单的推平方法采用正向的推平,即队伍第一个订单的开始时间是整个系统的起始时间。具体生产过程的流程如图 3所示。
|
图 3 系统工作流程 Fig. 3 Flow chart of system working process |
根据订单排队方法生产订单队列,再根据理论的生产加工时间可以计算出每个订单的完成时间。对于连续的加工过程,每个订单的加工耗时为:订单加工耗时=产品在瓶颈资源处加工时间×订单中产品数量,即OPTi=Qi×PTib(其中,PTib为产品Pi在瓶颈资源处加工时间)。那么,理论的订单完工时间=订单开始加工时间+订单加工耗时,即ICTi=ISTi+OPTi。
1.2.4 投料控制传统的DBR理论在投料时间安排上依据前文所述的静态缓冲管理方法,通过将缓冲区划分为3个不同的区域进行投料量以及投料时间的控制。本文采用一种全新的动态的缓冲管理方法,来对投料时间进行安排。
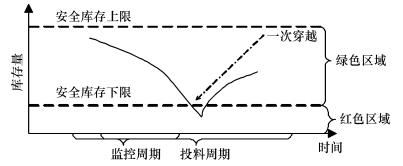
首先,对缓冲区分别设置一个安全上限和安全下限。其中安全上下限之间的区域为绿色区域,低于下限的区域为红色区域[17]。缓冲管理的目的就是通过合理的管理方法维持缓冲中的WIP库存在绿色区域。缓冲的划分如图 4所示。
|
图 4 缓冲划分示意图 Fig. 4 Buffer size |
接着,在如上的缓冲区添加2个独立运行的投料机制:周期投料与紧急投料。周期投料作为一种最基本的投料机制,自系统运行起,每隔一个周期进行一次投料,投料量=安全上限-WIP-计划投料但还未投放的量。周期投料的周期选择应大于静态管理的平均投料周期。在周期投料的基础之上,增加一个监控窗口(monitoring window, MW),根据前一个监控窗口期间缓冲区在制品数量的变动情况,在接下来的监控窗口中对缓冲区的安全限进行调节,进而实现缓冲区的动态管理。
将库存量由高于安全库存下限变化到低于安全库存下限定义为一次穿越,当缓冲中发生穿越时进行紧急投料。监控窗口的设置是希望通过减少投料量、增加投料次数来减少WIP库存。因此,监控窗口周期的选择应小于静态管理的平均投料周期。另外,考虑到频繁的投料会提高企业的生产成本,监控窗口时长的跨度应该以保证1次紧急投料为宜。那么,监控窗口的时长应该介于瓶颈工序消耗紧急投料量所用时间与静态管理平均投料周期之间。
综上所述,在监控窗口期间,尽量控制发生1次紧急投料。那么,既可以根据穿越次数与库存耗尽的情况对缓冲区的安全限进行动态的调节以及投料控制,具体可以分为以下3类5种调节。
1) 未出现穿越。
在1个监控窗口中,如果没有发生穿越情况,表明缓冲区容量太大,降低安全上限,同时重置监控窗口。
2) 穿越1次。
a.未出现WIP耗尽情形。在1个监控窗口中,仅出现穿越情况,进行紧急投料;
b.出现WIP耗尽情形。在发生穿越情况后,接着发生WIP耗尽情况,表明安全库存下限设置太低,上调安全库存下限,并重置监控窗口;
3) 穿越2次及以上。
a.未出现WIP耗尽情形。在1个监控窗口中,仅连续发生2次及以上穿越情况,表明安全库存下限设置太高,上调安全库存下限,并重置监控窗口;
b.出现WIP耗尽情形。在1个监控窗口中,连续发生2次及以上穿越情况,同时在最后一次跳变后紧接着发生库存耗尽的情形,表明缓冲容量不够,上调安全库存上限,并重置监控窗口。
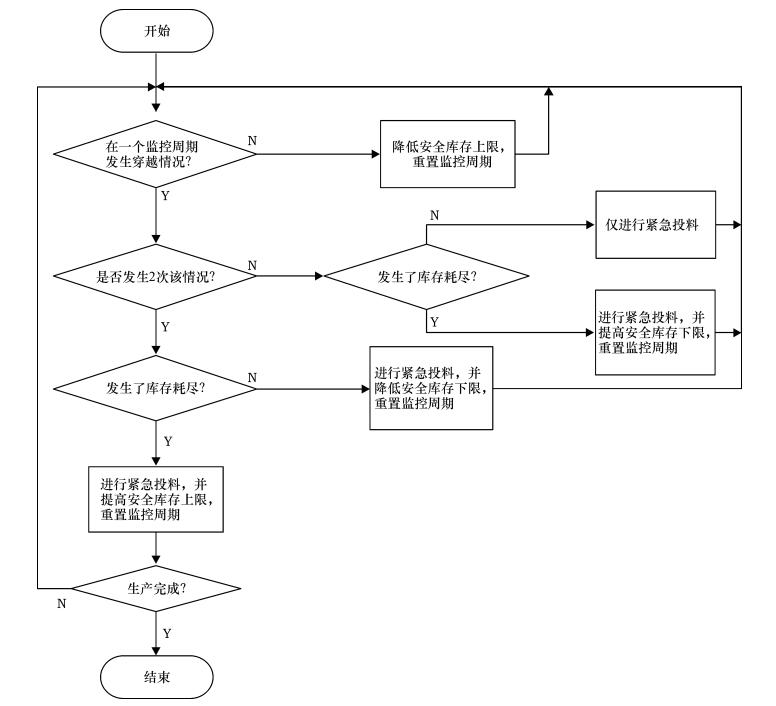
在各种情形下,紧急投料投料量=(安全上限-WIP)/2-计划投料但还未投放的量。一旦有调节安全限的情况发生,监控窗口就重新进行计数,具体工作流程如图 5所示。
|
图 5 监控窗口工作流程 Fig. 5 Flow chart of monitoring window |
本系统作为敏捷制造系统的一种实际应用。客户在关注产品质量的同时,对产品的如期交货比较注重,在制品库存是企业的重要关注点,因此本系统的3个主要评价指标如下。
1) 订单总延期时间
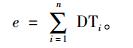
|
(3) |
其中, DTi为订单Oi的延误时间。为系统简化考虑本系统只考虑延期惩罚,不考虑提前交货库存惩罚; 同时假设所有订单延期惩罚系数一致,使用总延期时间来进行标识。
2) 平均在制品库存
在制品的考察通过统计的方式实现,具体为按照一定的周期检测缓冲区的在制品库存,最后使用求平均值的方法进行统计。在给定的时间段中,进行k次监控,每次监控的在制品库存为WIPl,则平均在制品库存为
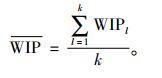
|
(4) |
3) 瓶颈工序利用率
系统的管理目的是通过维护瓶颈工序前的瓶颈缓冲的库存,保持瓶颈工序能够进行持续工作,避免产生瓶颈饥饿,因此本系统的瓶颈工序利用率也是系统的一个参考因素。瓶颈工序利用率的定义为:完成每个订单的生产加工时间段To中,瓶颈工序加工时间Tbusy的占比,即
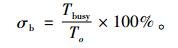
|
(5) |
其中, 瓶颈工序只存在2种状态:加工-busy; 空闲-idle。
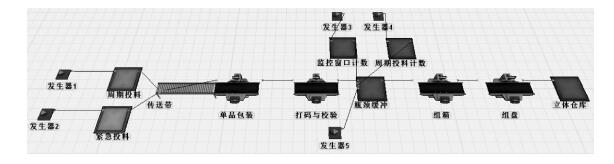
2 案例分析本文以酒类包装生产过程为例。通过对模型的参数分析,组箱环节是本系统的瓶颈资源,因此将瓶颈缓冲设置在组箱工作站前。整个生产过程通过仿真软件Flexsim进行建模仿真,具体仿真模型如图 6所示,模型中各生产环节的参数设置具体参见表 2所示。
|
图 6 生产系统Flexsim模型 Fig. 6 Simulation model using the software "Flexsim" |
| 表 2 产线参数 Tab. 2 Parameters of the line |
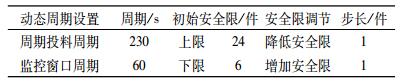
根据缓冲计算原则,缓冲区安全下限长度按照瓶颈工序前置时间的4倍设置,即MR=4。基于10组定性数据分析:缓冲区安全下限设置太低会导致瓶颈工序产生大规模的瓶颈饥饿; 缓冲区安全下限设置太高,会导致太多的在制品堆积在瓶颈缓冲中。安全上限设置原则也采用MR=4,即安全上限为安全下限的4倍。同样基于10组定性数据分析:安全上限设置太低或者太高,导致静态管理策略平均在制品库存与动态缓冲管理策略相比劣势越来越明显。根据经验值分别设置投料周期等参数,具体如表 3所示。
| 表 3 控制策略参数 Tab. 3 Parameters of the BM |
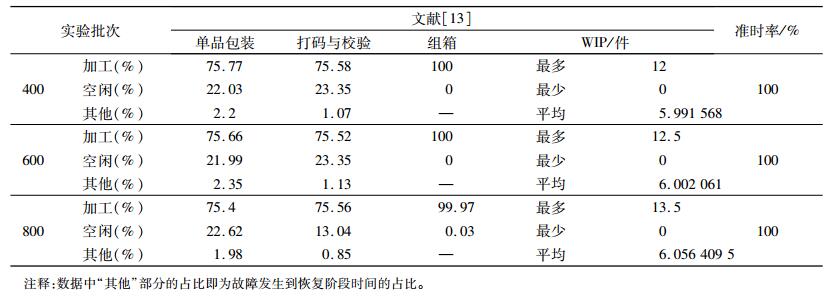
工作站单品包装以及打码与校验环节工作站都附带了平均故障率以及故障恢复时间的设置,故障设置采用浴盆曲线的偶然故障期[18]。另外,考虑到实际生产环境中瓶颈工序的产出存在一定的波动,仿真中瓶颈工序的处理速度使用期望为8的均匀分布。实验过程安排了3批次的产品进行仿真,实验产品规模分别为400件、600件以及800件,每个实验项目安排50次独立重复实验。同时,本文选择了基于静态缓冲管理方法实现的生产系统作为系统的主要参考对比,以及作为参考模型,本文也对文献[13]所介绍的动态方法进行实现。对实验结果进行平均统计,结果参见表 4~表 6所示。
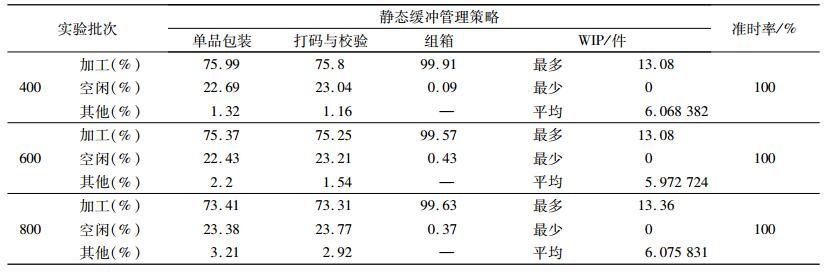
| 表 4 基于静态策略进行缓冲管理的生产数据 Tab. 4 Scheduling status with traditional method |
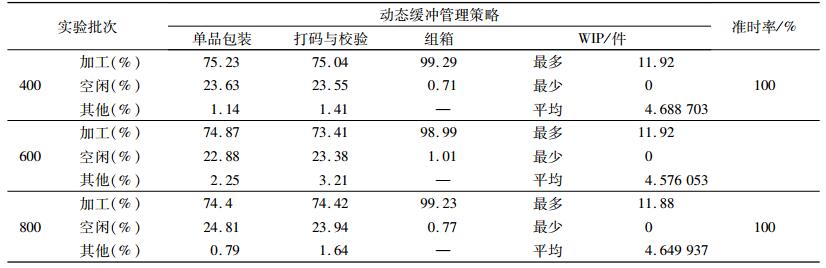
| 表 5 本文动态缓冲管理策略进行缓冲管理的生产数据 Tab. 5 Scheduling status with current dynamic method |
3种不同的管理策略,3项评价指标对比结果如表 7所示。
| 表 7 3种管理策略3项评价指标对比 Tab. 7 Table of 3 performance assessment indices and comparison for both method |
通过表 7所示的对比数据,对于3组不同规模的生产情况,基于动态管理策略和静态管理策略的生产结果完工准时率均为100%。在各方面生产数据一致的基础之上,采用动态管理策略的平均在制品库存相对于采用静态管理策略的平均在制品库存存在最少22.71%,最多23.47%的优势,且随着加工数量的增加优势呈对数级增长趋势。与此同时,采用动态管理策略的系统相对于静态管理策略的系统,瓶颈工序利用率仅存在最多0.7%的劣势(利用率均在98.6%以上)。与文献[13]所提供的动态缓冲管理方法相比,本文所讨论的动态管理方法存在明显的优势。由表 2所示数据,文献[13]所提供的方法在管理效果上与本文所采用静态缓冲管理方法的管理效果基本相同,在在制品数量基本相同的前提下,文献[13]的瓶颈工序利用率优于本文所采用的静态管理方法。
3 结论在传统DBR理论的基础之上,考虑酒类生产系统要求尽量少在制品库存的实际需求,本文给出了一种融合了动态缓冲管理机制的DBR方法的实现。针对传统的静态缓冲管理方法中太过依赖缓冲大小计算准确度的问题,本文在传统方法计算得到缓冲区的基础之上,增加一个监控窗口,在监控窗口中,根据缓冲区出现WIP库存由高于安全库存下限变化到低于安全下限的频率,再结合其后是否出现WIP库存耗尽的情形对缓冲区的安全上下限进行调节进而实现对缓冲区的动态管理。通过实验仿真的对比数据,肯定了这种动态管理方法的有效性。通过将该DBR方法应用到某酒厂实际产线,不但提高了生产过程中成本控制的效率,同时在原材料管理方面也可以使用库存管理方法,也提高了原材料管理的效率。
| [1] |
GOLDRATT E M, COX J, WHITFORD D. The goal: a process of ongoing improvement[M]. Great Barrington, MA: North River Press, 1992.
|
| [2] |
周峰. DBR管理模式的生产计划与控制机制探讨[J].
中国管理科学, 2000, 8(1): 17-21.
ZHOU Feng. Study on the production schedule and control mechanism in DBR[J]. Chinese Journal of Management Science, 2000, 8(1): 17-21. |
| [3] |
SCHRAGENHEIM E, RONEN B. Drum-buffer-rope shop floor control[J].
Production and Inventory Management Journal, 1990, 31(3): 18-22.
|
| [4] |
SCHRAGENHEIM E, RONEN B. Buffer-management: A diagnostic tool for production control[J].
Production and Inventory Management Journal, 1991, 32(2): 74-79.
|
| [5] |
郭永辉. Drum-Buffer-Rope理论研究综述[J].
工业工程与管理, 2008, 13(2): 1-4.
GUO Yong-hui. Review on Drum-Buffer-Rope theory[J]. Industrial Engineering and Management, 2008, 13(2): 1-4. |
| [6] |
李爱华, 尹柳营. DBR技术中确定缓冲大小的模型[J].
中国管理科学, 1998, 6(1): 16-20.
LI Aihua, YIN Liuying. A model for determining the size of time buffers in DBR[J]. Chinese Journal of Management Science, 1998, 6(1): 16-20. |
| [7] |
WU H H, YEH M L. A DBR scheduling method for manufacturing environments with bottleneck re-entrant flows[J].
International journal of production research, 2006, 44(5): 883-902.
DOI: 10.1080/00207540500362187. |
| [8] |
HUANG H H, PEI W, WU H H, et al. A research on problems of mixed-line production and the re-scheduling[J].
Robotics and Computer-Integrated Manufacturing, 2013, 29(3): 64-72.
DOI: 10.1016/j.rcim.2012.04.014. |
| [9] |
杨琴, 周国华, 林晶晶, 等. 基于DBR理论的柔性流水车间动态调度[J].
控制与决策, 2011, 26(7): 1109-1112.
YANG Qin, ZHOU Guo-hua, LIN Jing-jing, et al. Dynamic scheduling of flexible flow-shop problem based on DBR theory[J]. Control and Decision, 2011, 26(7): 1109-1112. |
| [10] |
SIVASUBRAMANIAN R, SELLADURAI V, RAJAMRAMASAMY N. The effect of the drum-buffer-rope (DBR) approach on the performance of a synchronous manufacturing system (SMS)[J].
Production Planning & Control, 2000, 11(8): 820-824.
|
| [11] |
RIEZEBOS J, KORTE G J, LAND M J. Improving a practical DBR buffering approach using Workload Control[J].
International Journal of Production Research, 2003, 41(4): 699-712.
DOI: 10.1080/0020754031000065485. |
| [12] |
KLUSEWITZ G, RERICK R. Constraint management through the drum-buffer-rope system[J].
Advanced Semiconductor Manufacturing Conference & Workshop, 1996, 11(1): 7-12.
|
| [13] |
徐云天, 张力菠. 考虑系统波动因素的DBR瓶颈缓冲区容量设置[J].
工业工程, 2014, 17(6): 24-29.
XU Yun-tian, ZHANG Li-bo. Determination of constraint buffer size for drum-buffer-rope considering system's fluctuation factor[J]. Industrial Engineering Journal, 2014, 17(6): 24-29. |
| [14] |
BECHTE W. Theory and practice of load-oriented manufacturing control[J].
The International Journal of Production Research, 1988, 26(3): 375-395.
DOI: 10.1080/00207548808947871. |
| [15] |
GUIDE V D, GHISELLI G A. Implementation of drum-buffer-rope at a military rework depot engine works[J].
Production and Inventory Management Journal, 1995, 36(1): 79-79.
|
| [16] |
CHAKRAVORTY S S. An evaluation of the DBR control mechanism in a job shop environment[J].
Omega, 2001, 29(4): 335-342.
DOI: 10.1016/S0305-0483(01)00028-7. |
| [17] |
YUAN K J, CHANG S H, LI R K. Enhancement of theory of constraints replenishment using a novel generic buffer management procedure[J].
International journal of production research, 2003, 41(4): 725-740.
DOI: 10.1080/0020754031000065502. |
| [18] |
黄祥瑞.可靠性工程[M].北京:清华大学出版社, 1990:15-16.
HUANG Xiang-rui. Reliability engineering[M]. Beijing: Tsinghua University Press, 1990:15-16. |
 2016, Vol. 19
2016, Vol. 19