随着市场竞争的日益激烈,而产品及其基本保修策略之间的差异减少,越来越多的生产商开始提供延伸保修以增强产品的市场竞争力,同时,其也成为企业利润新增长点。一般来说,耐用产品的使用寿命周期比质保期要长,延伸保修是在质保期结束后,由消费者和生产者签订的后续维修服务条款。延伸保修在欧美及日本等发达国家已有40多年的历史,已经发展成为一项非常成熟的产业,这些国家耐用产品延伸保修购买率已达到40%[1],国内的企业如联想、海尔、同方等也开始提供延伸保修服务[2]。
延伸保修对于用户和生产商双方都具有重要意义。当前用户更加注重产品在整个使用寿命周期内的成本。对于用户来说,寿命周期成本包括产品购买和使用维修费用,所以,生产商以较低的价格提供更加优质的延伸保修服务可以增强产品竞争力,提高市场份额;而对于用户来说,购买延伸保修服务可以在一定程度上规避产品失效风险成本[3],而且通过合理的决策可以增加产品使用寿命、减少产品寿命周期内的维护成本。
随着延伸保修的发展,国内外相应的研究也逐渐增多。Lam等[4]在以往延伸保修实证研究的基础上,对延伸保修进行了建模分析,通过确定用户是否选择延伸保修服务,分别得到了消费者和生产者单位时间内的期望费用;Jack等[5]提出了更具灵活性的延伸保修策略,通过决策延伸保修的起点和终点优化消费者和生产商的费用;Wu等[6]从消费者角度出发建模优化包括延伸保修在内的产品全寿命周期费用;Soumaya等[7]提出了不同维修策略下的延伸保修价格决策模型;在此基础上,卢震等[8-9]研究了产品质量影响下的延伸保修服务策略和定价模型;叶武等[10]建立了包括生产商、消费者、维修商三方的延保定价博弈模型,并得到了生产商利润最大策略。以上的研究大部分在延伸保修阶段只考虑了修复性维修,而合理实施主动的预防性维修通常可以减少产品总维修成本。且以上研究大多是从生产商利润角度出发,均未考虑延伸保修对产品使用寿命长度以及用户维修使用决策的影响。鉴于此,在考虑预防性维修和延伸保修对产品使用寿命影响的基础上,本文分析了产品寿命周期内生产商定价策略及用户维修成本组成,建立了延伸保修决策优化模型,并提出了有效解法,得出了生产商在延伸保修期内最优的预防性维修间隔期和次数以及用户最优延伸保修决策方案,在保证生产商利润的同时,降低产品使用寿命周期内维修成本。
1 产品寿命周期内生产商定价策略对用户来说,通常包含延伸保修的产品寿命周期L可以划分为3个阶段:质保期(初始保修期)W、延伸保修期We、用户责任期,如图 1所示。其中,初始保修一般包含在产品的销售合同中。

|
图 1 产品寿命周期阶段图 Fig. 1 Product life cycle stage |
相应地,对生产商来说,需要确定以下3种不同寿命周期阶段相应维修服务的价格。
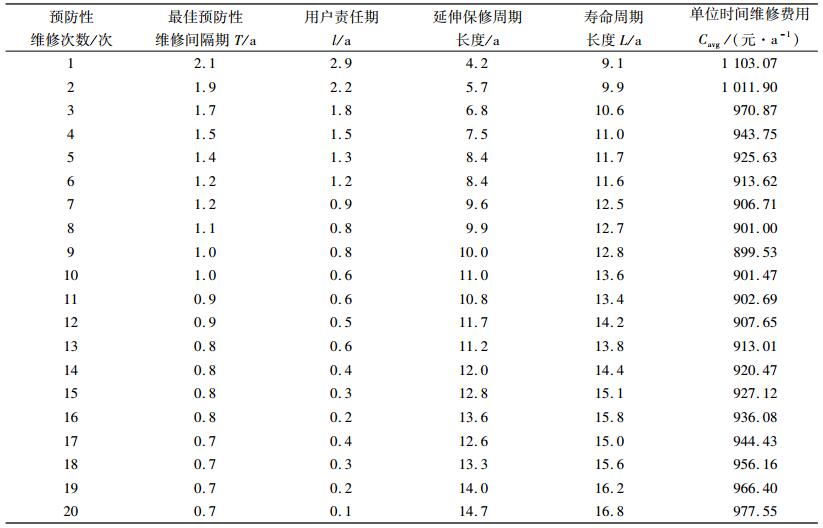
1) 延伸保修价格。在制定延伸保修价格时通常需要考虑成本因素和利润因素。所以,产品延伸保修价格可以表示为
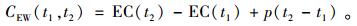
|
(1) |
其中,t1, t2分别为延伸保修开始和结束时间;EC(t2)-EC(t1)表示提供延伸保修服务成本;p为单位时间内生产商利润需求。
由式(1)可以看出,在保证生产商自身利润的情况下,想提供较低价格的延伸保修服务进而减少产品寿命周期成本,以提高用户满意度,增强产品市场竞争力和份额,有效的方法是降低延伸保修成本,而合理的预防性维修通常能够降低产品故障率,进而降低总维修成本。
2) 用户责任期维修费用(价格)。假设生产商对产品进行单次故障维修的成本为Cr。在质保期和延伸保修期外,产品故障后用户交由生产商或第三方修理机构修理的费用为CR,一般来说,存在CR≥Cr。
3) 产品更换价格。即用户需承担的产品更换成本(价格),同样,考虑生产商成本和利润因素,产品价格可表示为
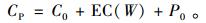
|
(2) |
其中,C0为产品生产成本;EC(W)为产品在质保期内的保修成本;P0为生产商利润。为方便分析,文中假设产品更换成本是固定的。
2 延伸保修决策优化模型 2.1 模型描述与假设本文假设研究的产品是一个可修复系统且具有老化特性。在质保期结束后,即开始延伸保修期,用户决策延伸保修期以及用户责任期长度,在用户责任期结束时对产品进行更换。为降低延伸保修成本,降低产品寿命周期成本,生产商在延伸保修期内对产品进行周期预防性维修。为方便分析,假设在延伸保修期内对产品进行N-1次预防性维修,在第N次时延伸保修期结束。对于在产品使用过程中出现的故障采用最小维修方式进行修复,即“修复如旧”。
由于维修时间相对于产品寿命周期来说很短,所以在模型中忽略停机时间的影响。产品寿命周期费用只考虑与维修更换相关的费用,虽然预防性维修能够降低产品故障率,但产品使用仍然是一个退化过程,在到达一定年限后需对其进行更换。在用户决策产品更换时机(使用寿命长度L)时,采用产品经济寿命理论[11],即在产品单位时间维修费用最低时进行更换。
2.2 预防性维修模型根据老化产品或部件具有衰退现象的特性,预防性维修对降低产品故障率起到很重要的作用,每次预防性维修后,产品的故障率特性都会发生变化。为描述预防性维修对产品故障率变化的影响,引入有效工龄(effective age)和改善因子(improvement factor)的概念[12]。产品故障率与有效工龄直接相关。如果所有故障均采取最小维修且维修时间忽略,有效工龄和日历时间相等。产品在预防性维修后,有效工龄会减少,而有效工龄的减少程度和改善因子相关。假设每次预防性维修的改善因子相同,均为α∈[0, 1],α越大说明预防性维修后,产品恢复程度越高。两次预防性维修间隔为Δt,那么预防性维修后,产品有效工龄减少量为αΔt。假设产品在延伸保修阶段的预防性维修周期为T,则第一次预防性维修间隔时间为Δt=W+T,那么第一次预防性维修后,产品有效工龄为
|
(3) |
即经过维修后,产品剩余寿命增加了α(W+T)。由于文中采用的是周期性预防性维修,所以,延伸保修阶段之后的预防性维修间隔时间均为Δt=T,那么,在第2次预防性维修之前,产品有效工龄可表示为
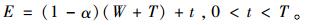
|
(4) |
同理,在经过第2次预防性维修后,有效工龄为
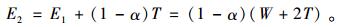
|
(5) |
在第3次预防性维修之前,产品有效工龄可表示为
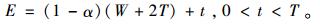
|
(6) |
以此类推,可得在第i次和i+1次预防性维修之间,产品有效工龄为
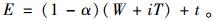
|
(7) |
此时,产品的故障率函数为
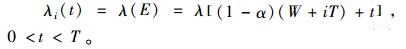
|
(8) |
其中,λi(t)表示第i次和i+1次预防性维修之间产品故障率函数;λ(t)表示初始故障率函数,此外,有λ0(t)=λ(W+t),t∈(0, T)。
2.3 产品单位时间维修费用模型对用户来说,产品在寿命周期内与维修相关的费用包括:延伸保修费用、用户责任期内维修费用、产品更换费用(即产品价格)。所以,用户在产品寿命周期内单位时间维修费用可表示为
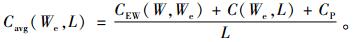
|
(9) |
其中,CEW(W, We)表示延伸保修价格;C(We, L)表示在用户责任期内的总维修成本;CP为产品价格;L为产品使用寿命长度。
为方便分析,假设生产商在延伸保修期内对产品进行N-1次预防性维修,在第N次时延伸保修期结束,则有We-W=NT。令l=L-We,即为延伸保修结束后,产品继续使用时间。则产品使用寿命周期长度可表示为
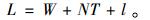
|
(10) |
所以,用户单位时间内维修费用可以转换为
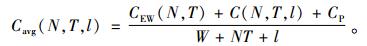
|
(11) |
假定Cmi为第i次预防性维修费用,因为产品随着使用会不断老化,因此要使产品维修后的状态得到恢复,预防性维修费用会不断增加,所以文中将预防性维修费用分为固定费用Cf和变动费用Cv[12]。所以,第i次预防性维修费用可表示为
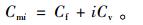
|
(12) |
由上式可以看出预防性维修费用随着产品使用及维修次数的增加而增加。由于最小维修后产品的故障率不发生变化,为方便分析,假定最小维修费用Cr为固定值。
由式(1)可知,延伸保修价格CEW(N, T)包括延伸保修成本和生产商利润两部分组成。其中,延伸保修成本含预防性维修费用和修复性维修两部分。假设对故障均采用最小维修进行修理,而最小维修特性是一个非齐次泊松过程(NHPP)[13],由预防性维修下产品故障率函数式(8)可以得出在第i个预防性维修周期内产品故障次数期望值。
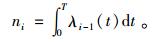
|
(13) |
所以,产品延伸保修价格可表示为
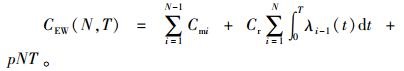
|
(14) |
产品在用户责任期内的维修成本即故障最小维修费用,经过N-1次预防性维修,在延伸保修结束时产品有效工龄为
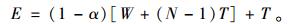
|
(15) |
所以在用户责任期内,产品故障率函数可表示为
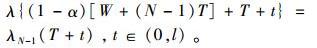
|
(16) |
在用户责任期内,维修费用由消费者承担,所以,这一阶段维修总费用可表示为
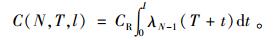
|
(17) |
将式(12)~(17)带入式(11)中,可得单位时间内产品维修费用表达式为
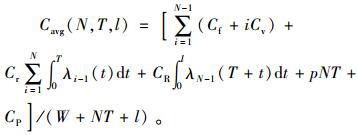
|
(18) |
综上所述,可以得到如下延伸保修决策优化模型:
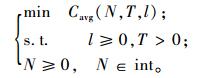
|
(19) |
当用户不购买延伸保修服务时,即W=We,在质保期结束至产品之前总维修费用为
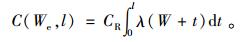
|
(20) |
此时,产品在使用寿命周期内的单位时间维修费用为
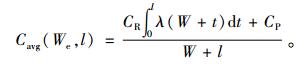
|
(21) |
以上给出了延伸保修决策优化模型,用以确定最优的延伸保修期、产品的使用寿命和最佳的预防性维修策略。可以看出,优化模型式(19)结构比较复杂,存在非线性关系,且决策变量较多,模型很难得到关于目标的解析表达式,尤其是当故障函数本身形式比较复杂时。为增强模型的适用性,可以运用网格搜索(grid search)算法得到模型最优化结果,网格搜索用于优化的关键是根据已有的先验条件划分合适的网格,构造恰当的适应函数对每个格点进行计算。网格搜索法是在实验区间内以固定步长逐点进行计算的,可避免因代价函数存在多个极值而导致的局部优化,因而能找到最优解[14]。
可以根据同类产品的故障特点及寿命周期长度等数据,结合产品实际使用情况,确定各决策变量的变化区间及对应的步长。然后,运用Matlab软件编程计算各个格点对应的单位时间维修费用值,通过比较可以得到最优的延伸保修决策方案。模型优化流程如图 2所示。
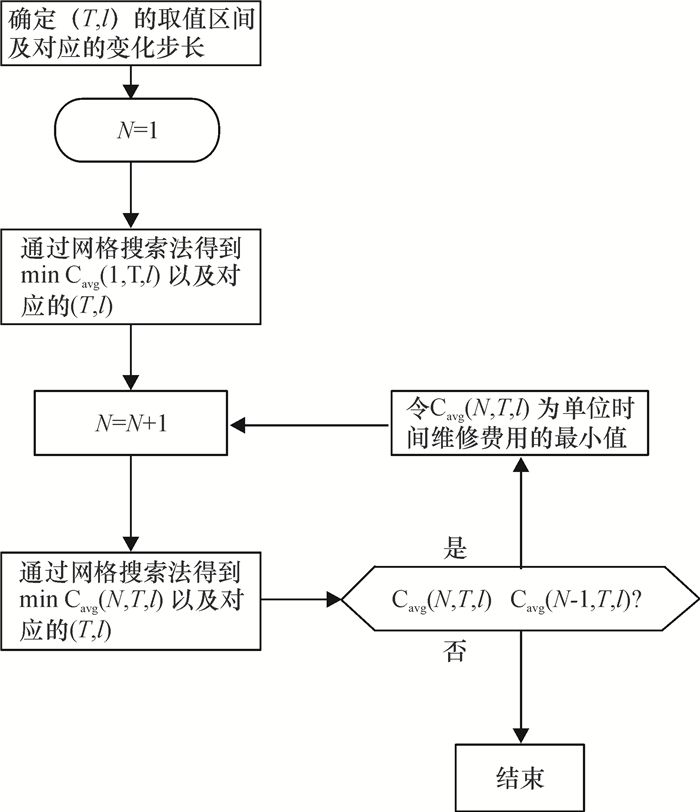
|
图 2 模型优化流程示意图 Fig. 2 The optimization process of model |
为了验证上述优化模型和算法的有效性,给出了以下算例进行分析。假定某产品的故障规律服从威布尔(Weibull)分布:
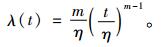
|
其中,形状参数m=2,尺度参数η=2,此时,产品首次故障时间期望为1.77a。产品的质保期W=2a,为增加产品市场竞争力,生产商提供延伸保修服务,并在延伸保修期内进行预防性维修以降低消费者寿命周期内维修费用,延长产品使用寿命长度。其余相关参数设置如表 1所示。
| 表 1 相关参数设置 Tab. 1 The values of relevant parameters |
为方便计算描述,在以下分析中设置时间单位统一为年,费用单位为元。
在实际应用中,预防性维修周期过短不仅会给用户使用带来不便,也会增加生产商的成本。所以算例设定T以步长0.1在区间[0.1, 5]内变化;l以步长0.1在区间[0, 3]内变化。运用上文所给出的优化模型及算法,可以得到不同N值下的单位时间维修费用。N=8即预防性维修次数为7次时,单位时间维修费用随(T,l)的变化情况如图 3所示。
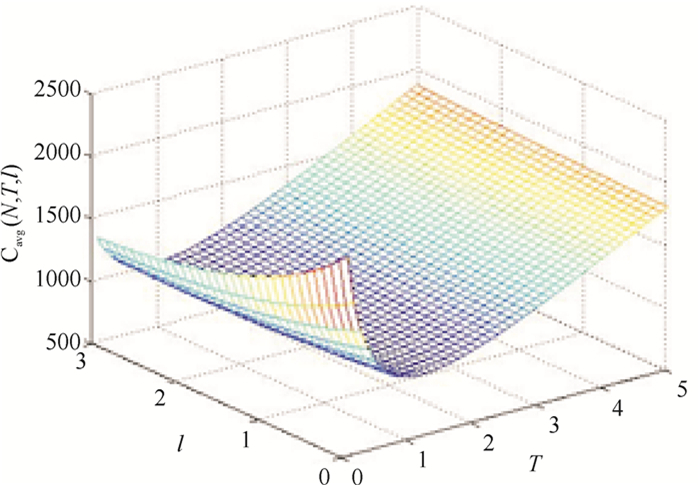
|
图 3 单位时间维修费用变化趋势图 Fig. 3 Variation trend of the maintenance cost of unit time |
为便于对三维图形的直观分析,此处对三维图形进行降维解析,效果如图 4、图 5所示。
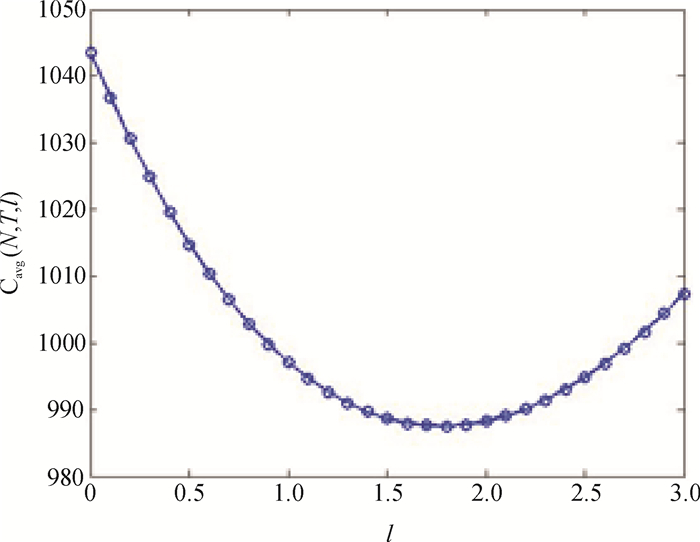
|
图 4 l-Cavg趋势图 Fig. 4 Variation trend of l-Cavg |
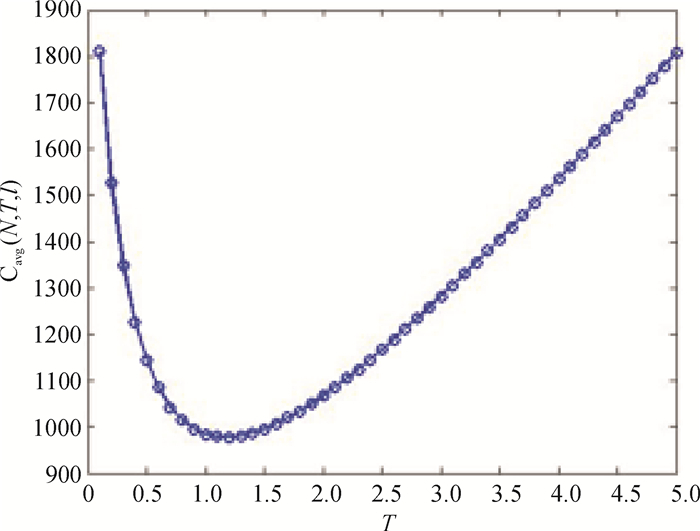
|
图 5 T-Cavg趋势图 Fig. 5 Variation trend of T-Cavg |
图 4表示用户责任期长度l对单位时间维修费用的影响;图 5表示预防性维修周期T对单位时间维修费用的影响。由这2个图的变化趋势可以看出,当2个变量中任何一个确定时,存在最优的决策值使得产品单位时间维修费用最小,如图所示,当2个变量取(1, 1.5)之间某个值时,目标函数达到最优。图 3说明在不同的N值下,当(T,l)取值变化时,对应的单位时间维修费用存在最小值。
基于上述分析,可以得到不同N值下对应的目标函数最优值,如图 6所示。
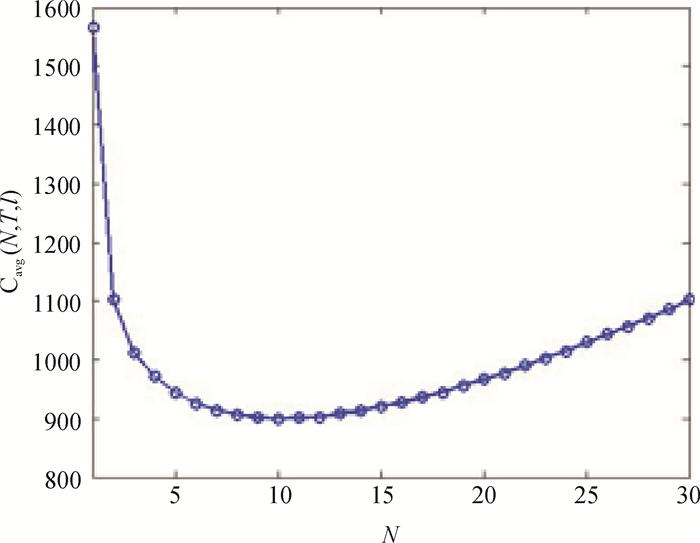
|
图 6 N-Cavg(N, T, l)趋势图 Fig. 6 Variation trend of N-Cavg(N, T, l) |
由图 6可以看出,随着N值的不断增大,产品单位时间维修费用先减少后增大,在N=10,即在延伸保修期内进行9次预防性维修时达到最小值899.53元/a。模型部分详细优化结果如表 2所示。
| 表 2 产品延伸保修决策模型优化结果 Tab. 2 The optimization results of product extended warranty decision model |
当用户不购买延伸保修时,由式(20)可得此时最小的单位时间维修费用及相关决策变量值。
Cavg(We, l)=1 624.8,l=3.4。
此时,产品使用寿命长度为:L=W+l=5.4。
当N=1时,即生产商在延伸保修期内不进行预防性维修,运用上文的分析计算方法,得到对应的优化值及决策变量为
Cavg(N, T, l)=1 566.3,T=3.9,l=0。
此时,产品使用寿命长度为
L=W+NT+l=5.9。
由表 2可以看出,随着延伸保修期内预防性维修次数的增加,最佳的预防性维修间隔期总体趋势不断减小,用户责任期长度也呈下降趋势。这是由于随着产品使用时间的增长,故障率不断升高,此时预防性维修间隔期减少可以更有效的降低故障发生次数,降低维修费用;而在用户责任期内没有预防性维修,所以当故障率较高时继续使用会导致维修费用的快速增加。
延伸保修周期长度和产品使用寿命长度随预防性维修次数的增加不断增长。可以看出,当预防性维修次数为9时,产品单位时间内维修费用最小。所以,延伸保修最优决策方案相关参数值为
Cavg(N, T, l)=899.53,N=10,T=1.0,l=0.8。
此时延伸保修周期长度为10.0,产品使用寿命长度为
L=W+NT+l=12.8。
对比不购买延伸保修的情况,延伸保修最优决策方案单位时间维修费用降低了44.64%,产品使用寿命长度增加了137.04%;对比生产商在延伸保修期内不采取预防性维修的情况,延伸保修最优决策方案单位时间维修费用降低了42.57%,产品使用寿命长度增加了116.95%,并且满足了生产商在延伸保修期内的利润需求,充分验证了模型的科学性和优越性。
所以,在质保期结束后,用户最优策略是选择10a的延伸保修,并在产品使用达到12.8a时对产品进行更换;而对应的生产商应在延伸保修期内进行9次周期性预防性维修,这样可以在保证自身利润的前提下,降低产品使用维修费用,并延长产品使用寿命周期,提高产品市场竞争力。
5 结束语本文针对产品延伸保修的最优决策问题,从产品寿命周期费用出发,分析了生产商各个阶段的定价策略,在此基础上建立了用户在产品寿命周期内单位时间维修费用模型,并进行了优化。得到了生产商提供延伸保修服务的最佳预防性维修策略,既保证了自身利润,也降低了用户使用产品的维修成本,提高了产品市场竞争力。通过对用户购买延伸保修长度及更换时机决策的优化,大大降低了产品的维修成本,延长了产品的使用寿命。这为生产商和用户双方制定延伸保修决策方案提供了理论依据及实际参考。
| [1] |
THOMAS J M. Consumer perceptions of extended warranties[J].
Journal of Retailing and Consumer Services, 2007, 14(3): 224-231.
DOI: 10.1016/j.jretconser.2006.09.003. |
| [2] |
王素娟, 胡奇英. 基于延保服务吸引力指数的服务模式分析[J].
计算机集成制造系统, 2010, 16(10): 2277-2284.
WANG Sujuan, HU Qiying. Service modes analysis based on extended warranty services desirability index[J]. Computer Integrated Manufacturing Systems, 2010, 16(10): 2277-2284. |
| [3] |
SU C, SHEN J Y. Analysis of extended warranty policies with different repair options[J].
Engineering Failure Analysis, 2012, 25: 49-62.
DOI: 10.1016/j.engfailanal.2012.04.002. |
| [4] |
LAM Y, LAM P K W. An extended warranty policy with options open to consumers[J].
European Journal of Operational Research, 2001, 131(3): 514-529.
DOI: 10.1016/S0377-2217(00)00091-6. |
| [5] |
JACK N, MURTHY D N P. A flexible extended warranty and related optimal strategies[J].
The Journal of the Operational Research Society, 2007, 58(12): 1612-1620.
DOI: 10.1057/palgrave.jors.2602326. |
| [6] |
WU S M, PHIL L. Optimising age-replacement and extended non-renewing warranty policies in life cycle costing[J].
International Journal of Economics, 2011, 130(2): 262-267.
|
| [7] |
SOUMAYA B, ANIS C, NIDHAL R. A decision model for adopting an extended warranty under different maintenance policies[J].
International Journal of Production Economics, 2012, 135(2): 840-849.
DOI: 10.1016/j.ijpe.2011.10.022. |
| [8] |
卢震, 张剑. 考虑质量成本的延保定价策略[J].
东北大学学报:自然科学版, 2013, 34(5): 744-747.
LU Zhen, ZHANG Jian. On the extended warranty pricing strategy considering the quality cost[J]. Journal of Northeastern University:Natural Science, 2013, 34(5): 744-747. DOI: 10.12068/j.issn.1005-3026.2013.05.032. |
| [9] |
聂佳佳, 邓东方. 产品质量影响延保成本下的延保服务外包策略[J].
工业工程与管理, 2014, 19(3): 26-33.
NIE Jiajia, DENG Dongfang. Manufacturer extended warranty services outsourcing strategy when product quality affect the cost of the extended warranty[J]. Industrial Engineering and Management, 2014, 19(3): 26-33. |
| [10] |
叶武, 邵晓峰. 产品质量保证的延保定价研究[J].
西南民族大学学报:自然科学版, 2014, 38(6): 1001-1006.
YE Wu, SHAO Xiaofeng. Setting price of extended warranty[J]. Journal of Southwest University for Nationalities:Natural Science Edition, 2014, 38(6): 1001-1006. |
| [11] |
甘茂治, 康建设, 高崎.军用装备维修工程学[M].北京:国防工业出版社, 2005:317-318.
|
| [12] |
宋之杰, 杨志秀, 赵玉忠, 等. 可用度及动态维修成本下的维修决策模型[J].
工业工程, 2014, 17(2): 17-22.
SONG Zhijie, YANG Zhixiu, ZHAO Yuzhong, et al. A maintenance decision-making model based on the availability and dynamic maintenance costs[J]. Industrial Engineering Journal, 2014, 17(2): 17-22. |
| [13] |
PASCUAL R, ORTEGA J H. Optimal replacement and overhaul decisions with imperfect maintenance and warranty contracts[J].
Reliability Engineering and System Safety, 2006, 91(2): 241-248.
DOI: 10.1016/j.ress.2005.01.018. |
| [14] |
XIE Y Q, WANG Y, ZHU P C, et al. Grid-search-based hybrid TOA/AOA location techniques for NLOS environments[J].
IEEE Communications Letters, 2009, 13(4): 254-256.
DOI: 10.1109/LCOMM.2009.082218. |
 2016, Vol. 19
2016, Vol. 19