产品保证是制造商向消费者提供的契约性协议,用以规范制造商对其所销售产品的权利和义务[1]。在正常使用条件下,若产品在保证范围内发生失效,顾客有权向制造商提出保证索赔,制造商需对失效产品进行维修、更换或赔偿。产品在保证范围内的性能对顾客的满意度有重要影响,可以认为,顾客满意度为顾客继续购买制造商产品的可能性[2]。若产品失效过于频繁,顾客的满意度将迅速下降,最终可能导致顾客转向购买其他竞争厂商的产品。
保证政策包含两个要素:1)保证所包含的范围;2)保证支付或赔偿给顾客的方式。根据产品保证维度变量,一般可以将保证政策分为一维保证和多维(维度变量≥2)保证两种[3]。通常的产品保证维度变量有购买时间、使用程度、使用周期数等。在保证范围内,制造商根据保证政策的规定为产品提供保证服务,保证服务成本的大小与制造商在保证范围内实行的维修策略密切相关。Pham和Wang[4]根据维修程度θ∈0, 1的不同,将维修分为最小维修(θ=0)、不完美维修(0 < θ < 1)和完全维修(θ=1)3种类型。最小维修将失效产品修复到失效前的状态,也称之为“恢复如旧”维修;非完美维修将失效产品修复至“如旧”和“如新”状态之间;完全维修则表示将失效产品修复如新,也等同于更换策略。制造商实行的维修策略会对保证服务成本产生重要影响。在一维保证政策下,Nguyen[5]以时间为维度,将产品保证期划分为维修区间和更换区间两部分,首次构建最小维修-更换策略下的保证服务成本分析模型,获得了使制造商期望保证服务成本最小化的更换区间;Jack和Schouten[6]认为Nguyen[5]得到的维修策略是次优的,将保证期间划分为3个阶段,在第一个阶段和第三个阶段实行最小维修,在第二个阶段根据产品在失效时的使用寿命决定实行最小维修或更换,构建此策略下的保证分析模型,求解获得使制造商保证服务成本最小的维修-更换策略。Yeh等[7]分析了当产品失效率增加时,可更新的免费更换保证政策对产品寿命更换策略的影响。Pascual和Ortega[8]假定制造商对产品实行最小维修、非完美大修和更换三种维修行为,通过构建制造商在产品寿命期内的总体期望维修成本模型,确定了使制造商维修成本最小的产品寿命期限,以及非完美大修间隔。Chien[9]在可更新免费保证以及比例付费保证政策下,将产品寿命期分为免费保证期,比例付费保证期以及后保证期三个阶段,构建制造商的期望总体保证服务成本模型,以成本最小化为目标,求解获得产品的最优更换寿命。在二维保证政策下,Iskandar和Murthy[10]以使用时间和使用程度为两个维度,构建矩形决策空间,获得了使制造商期望保证成本最小的维修-更换策略。在此基础上,Iskandar等[11]进一步将二维矩形决策空间划分为三个子空间,在第二个区间对产品的首次失效实行更换策略,其他区间内的产品失效均采取最小维修,并比较此维修策略与以往文献所提出的策略的优劣。Varnosafaderani和Chukova[12]将上述研究扩展为一般情况,将二维矩形决策空间划分为k个矩形子空间,在每个子空间内,制造商对产品的首次失效均采取非完美维修,对后续失效采取最小维修,以制造商的期望保证服务成本最小化为目标,分析获得最优的空间划分方式以及非完美维修的程度。Shahanagi等[13]在二维延伸保证政策下,假设制造商同时实行非完美预防性维修和最小维修策略,通过构建制造商在保证范围内的期望保证成本分析模型,分析获得使制造商保证成本最小的预防性维修策略。
上述文献着重于寻求如何使制造商保证服务成本最小化的保证服务策略,并无考虑产品失效带来的顾客的满意度下降对制造商造成的隐性损失。已有的保证分析模型多数面向一维保证政策,尚缺乏同时考虑顾客满意度和二维保证的维修策略研究。本文针对二维保证政策,将顾客满意度对制造商在保证范围内的期望总成本影响考虑在内,分别构建制造商在最小维修策略和大修策略下的期望总成本分析模型,其中,制造商的期望总成本分为保证服务成本和顾客满意度下降所产生的惩罚成本两部分。通过两阶段过程分析获得使制造商期望总成本最小的大修策略。最后将最优大修策略与最小维修策略进行对比,验证大修策略的优越性。
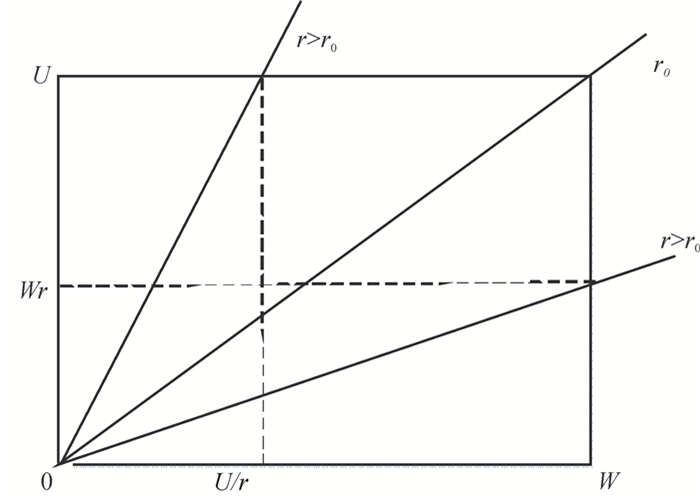
1 二维保证政策在二维保证政策下,通常选取使用寿命和使用程度作为产品保证的二维变量[14]。例如,汽车产品作为二维保证领域的代表性研究对象,在销售时通常附带一个2年/6万km的保证政策,这表示从汽车的购买时间算起,若汽车的使用寿命超过2年,或者行驶里程超过6万km,则保证政策终止。如图 1所示,在二维保证政策下,假设产品的使用寿命上限和使用程度上限分别为W和U,则产品保证范围是一个矩形区域Ω=[W, U]。其中, 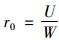
|
图 1 二维保证范围 Fig. 1 Two-dimensional warranty coverage |
假设产品的实际使用率为r,r≥0。对于不同用户,r是一个非负随机变量。r的常见分布有均匀分布和Gamma分布。当产品的实际使用率r < r0,表示顾客对产品的使用率较低,保证政策在产品的使用寿命达到W时终止,此时产品的实际使用程度为Wr,实际的保证范围为[W, Wr];当产品的实际使用率r>r0,表示顾客对产品的使用率较高,保证政策在产品的使用程度达到U时终止,此时产品的实际使用寿命为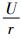
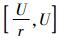
在构建成本分析模型之前,模型的若干假设列举如下。
●制造商为顾客所购买的产品提供二维免费维修保证政策,从产品售出之日起,到保证政策终止前,制造商为失效产品提供免费维修;
●与产品的平均失效间隔相比,制造商对失效产品的修复时间忽略不计;
●在正常使用产品的情况下,用户向制造商所提出的保证索赔均合理;
●在保证范围内,用户接受制造商提供的维修策略,并在产品失效后立即要求保证服务。
模型中所涉及的数学符号及含义如表 1所示。
| 表 1 数学符号及含义 Tab. 1 Mathematical notation and description |
顾客对产品的满意度取决于产品在保证范围内发生失效的次数NΩ。随着使用寿命x和使用程度u的增加,产品发生失效的概率也随之上升。给定NΩ=k,在产品保证政策结束后,顾客继续购买制造商产品的概率φ(k)为一个分段函数。
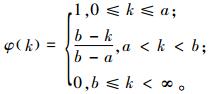
|
(1) |
根据式(1)可知,当产品在保证范围内的失效次数不超过a,顾客一定继续从原来的制造商处购买新的产品。当产品在保证范围内的失效次数大于a,φ(k)的值将逐渐下降,表示随着产品失效次数的增加,顾客对产品的满意度逐渐降低。当产品的失效数大于b,φ(k)降至为0,表示顾客将不会再从制造商那里购买新的产品。
本文分别考虑2种类型的维修策略。
●最小维修策略。在这种策略下,制造商对失效产品采取最小维修,维修后的产品失效率与失效前相同。
●(m, δ)大修策略。在这种策略下,制造商对产品的前m-1次失效均采取最小维修,如果产品在保证范围内发生第m次失效,则实行大修,如果产品在保证政策结束后发生第m次失效,则不进行大修。
在时间间隔[0, x)内,若制造商对失效产品采取最小维修,则{N(x|r), x≥0}是一个非齐次泊松过程。在使用寿命s和使用寿命t期间,产品发生k次失效的概率pk(s, t)为
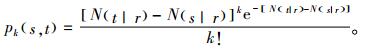
|
(2) |
将顾客的满意度对制造商在产品保证范围内总成本的影响考虑在内,制造商的期望总成本TCΩ等于制造商的期望保证服务成本ECΩ和制造商失去顾客的期望惩罚成本PCΩ之和。

|
(3) |
在最小维修策略下,为获得TCΩ,需根据产品的实际使用率考虑2种情况:r < r0和r>r0。
情况1:r < r0。在此种情况下,部件的实际使用率r小于r0,保证政策在产品的使用寿命达到W时终止,顾客继续购买制造商产品的概率为

|
(4) |
制造商在产品保证范围内的期望惩罚成本为
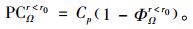
|
(5) |
制造商在产品保证范围内的期望保证服务成本表示为
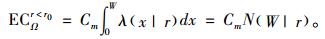
|
(6) |
综合式(5)和式(6),当r < r0,制造商在保证范围内的期望总成本TCΩr < r0表示为
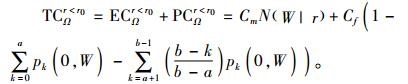
|
(7) |
情况2:r>r0。在此种情况下,产品的实际使用率r大于r0。保证政策在产品的使用程度达到U时终止,此时产品的实际使用寿命为
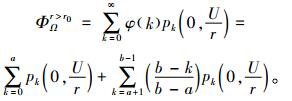
|
(8) |
则制造商承担的期望惩罚成本为

|
(9) |
制造商在产品保证范围内的期望保证服务成本表示为

|
(10) |
综合式(9)和式(10),当r>r0,制造商在保证范围内的期望总成本TCΩr>r0表示为

|
(11) |
综合r < r0和r>r0 2种情况,在最小维修策略下,制造商在保证范围内的期望总成本为

|
(12) |
在(m, δ)大修策略下,制造商对产品在保证范围内的前m-1次失效采取最小维修,如果产品在保证范围内发生第m次失效,则实行大修;如果产品在保证政策终止后发生第m次失效,则不进行大修。大修对产品可靠性产生的影响通过使用寿命削减法进行描述。假设当产品在使用寿命为x时实行大修,则维修后产品的实际使用寿命变为δx,0≤δ≤1。当δ=0,表示完美维修,相当于更换新的产品。当δ→1,表明维修的程度逐步下降。Co(δ, x)为制造商实行大修的单位期望成本,表示为

|
(13) |
根据式(13)可知,当δ=1,Cp(δ, x)=Cm,这时大修等同于最小维修。在(m, δ)大修策略下,同样需根据产品的实际使用率分两种情况进行分析:r < r0和r>r0。
情况1:r < r0。在此种情况下,当产品的实际使用寿命x达到W时,保证政策终止。产品在保证范围内的失效次数NΩr < r0=k的概率为

|
(14) |
则顾客继续购买制造商产品的概率为

|
(15) |
制造商对产品实行大修的概率为
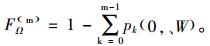
|
(16) |
产品在保证范围内的期望失效次数为
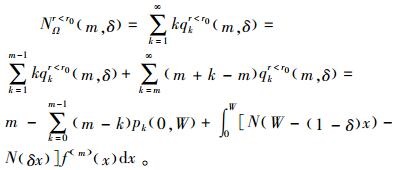
|
(17) |
当m保持不变,对δ取导,有

|
(18) |
由式(18)可知,NΩr < r0(m, δ)是δ的递增函数,这表示在保证范围内,产品的失效次数会随着大修程度的降低而增加。若δ保持不变,当m→∞,有NΩr < r0(m, δ)→N(Ω),表示随着m的增加,大修发生的概率会随之降低,(m, δ)大修策略最终近似为最小维修策略。
为获得制造商的期望保证服务成本ECΩr < r0(m, δ),需要考虑2种情况:NΩr < r0 < m和NΩr < r0≥m。当NΩr < r0=k < m,制造商对失效产品实行最小维修,保证服务成本为kCm。当NΩr < r0=k≥m,保证服务则为(k-1)Cm+Co(δ, x)。因此,制造商的期望保证服务成本等于

|
(19) |
式(19)中的第1项表示最小维修所对应的期望保证服务成本; 第2项表示当产品在保证范围内发生第m次失效,制造商采取大修所产生的额外期望保证服务成本。若固定m的值,第1项的值会随着δ的增加而增加,第2项则会随着δ的增加而减少。若固定δ的值,当m→∞,则有ECΩr < r0(m, δ)→CmNΩr < r0(m, δ),这表示当大修发生的概率越来越低时,制造商的期望保证服务成本最终等于最小维修所产生的期望保证服务成本。
制造商因顾客满意度下降所承担的惩罚成本PCΩr < r0为

|
(20) |
综合式(19)和式(20),当r < r0,制造商的期望总成本等于

|
(21) |
情况2: r>r0。在此种情况下,当产品的使用程度达到U时,保证终止,此时产品的实际使用寿命为

|
(22) |
顾客继续购买制造商产品的概率为

|
(23) |
制造商在保证范围内对产品实行大修的概率为

|
(24) |
在保证期
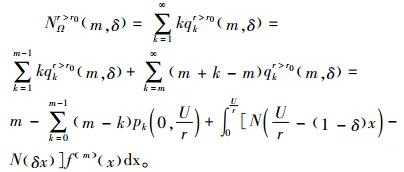
|
(25) |
考虑2种情况:NΩr>r0 < m和NΩr>r0≥m,当NΩr>r0=k < m,制造商对失效产品采取最小维修,保证服务成本为kCm。当NΩr>r0=k≥m,保证服务成本为(k-1)Cm+Co(δ, x)。因此,制造商的期望保证服务成本ECΩr>r0(m, δ)为

|
(26) |
制造商由于顾客满意度下降而承担的期望惩罚成本PCΩr>r0(m, δ)为

|
(27) |
综合式(26)和式(27),制造商在保证范围内的期望总成本为

|
(28) |
综合r < r0和r>r0 2种情况,在(m, δ)大修策略下,制造商在保证范围内的期望总成本TCΩ(m, δ)表示为

|
(29) |
根据式(29),模型中的决策变量为m和δ。在m≥1和0≤δ≤1约束下,以制造商的期望总成本TCΩ(m, δ)最小化为目标,可寻求最优的(m, δ)大修策略。
3 算例分析本算例以某半导体企业为汽车安全气囊系统所设计的型号为MMA2201传感器为研究对象,该传感器附带一个2年/4万km的保证政策,则W=2,U=4,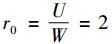

|
(30) |
这表示当产品在保证范围内的失效次数超过两次,顾客将不再继续购买制造商的产品。制造商失去一个顾客的惩罚成本为Cf=1 000。
在最小维修策略下,根据式(1)、(2)和(4)计算可得,顾客继续购买制造商产品的概率只有36.49%。产品在保证范围内的期望失效次数N(Ω)为2.52,根据式(12),制造商的期望总成本TCΩ=787.26(元)。
考虑(m, δ)大修策略,以MATLAB为平台,寻找使TCΩ(m, δ)最小的m和δ值。首先固定δ的值,通过最小化TCΩ(m, δ)寻求m*(δ);再通过最小化TCΩ(m*(δ), δ)寻求最优值δ*,以及m*=m*(δ*)。表 2列出了使制造商在产品保证范围内的期望总成本TCΩ(m, δ)最小的(m, δ)大修策略。可以发现m*(δ)=1,期望总成本TCΩ(m*(δ), δ)的值随着δ的增加而增加。根据表 2可知,(1, 0)策略为最优的大修策略,表示当产品在保证范围内发生第一次失效以后,制造商采取完美大修,此后对失效产品均采取最小维修。在最优大修策略下,制造商的期望总成本TCΩ(1, 0)为611.34元,顾客继续购买制造商产品的概率ΦΩ(1, 0)=0.614 7。与最小维修策略所对应的期望总成本相比,通过实行大修策略,制造商的的期望总成本降低了22.34%,顾客继续购买制造商的产品的概率从36.49%上升到61.47%,表示大修策略能够降低制造商的期望总成本,同时提升顾客对产品的忠诚度。
| 表 2 最优的(m, δ)大修策略 Tab. 2 the optimal(m, δ)overhaul strategy |
顾客对所购买产品的满意度取决于产品在保证范围内的性能,产品失效将导致顾客满意度的下降。本文在对以往面向保证的产品维修策略研究回顾的基础上,从制造商的角度出发,在二维保证政策下,将顾客的满意度对制造商期望总成本的影响考虑在内,分别构建了制造商在最小维修策略和(m, δ)大修策略下的期望总成本分析模型。以汽车安全气囊系统中的传感器为实际应用范例,通过两阶段过程方法,分析求解获得使制造商期望总成本最小的大修策略。研究表明,与最小维修策略进行对比,大修策略能有效降低制造商的期望总成本,同时提升顾客的重复购买概率。
| [1] |
MURTHY D N P, DJAMALUDIN I. Product warranty and reliability[J].
Annals of Operations Research, 2006, 143(1): 133-146.
DOI: 10.1007/s10479-006-7377-y. |
| [2] |
MURTHY D N P, JACK N. Warranty servicing strategies to improve customer satisfaction[J].
IMA Journal of Management Mathematics, 2004, 15(2): 111-124.
DOI: 10.1093/imaman/15.2.111. |
| [3] |
BLISCHKE W R, MURTHY D N P. Product warranty management - I: A taxonomy for warranty policies[J].
European Journal of Operational Research, 1992, 62(2): 127-148.
DOI: 10.1016/0377-2217(92)90242-2. |
| [4] |
PHAM H, WANG H Z. Imperfect maintenance[J].
European Journal of Operational Research, 1996, 94(4): 425-438.
|
| [5] |
NGUYEN D G. Studies in warranty policies and product reliability[D]. Australia: The University of Queensland, 1984.
https://www.researchgate.net/publication/34064435_Studies_in_warranty_policies_and_product_reliability
|
| [6] |
JACK N, VAN DER DUYN SCHOUTEN F. Optimal repair-replace strategies for a warranted product[J].
International Journal of Production Economics, 2000, 67(1): 95-100.
DOI: 10.1016/S0925-5273(00)00012-8. |
| [7] |
YEH R H. Optimal age-replacement policy for nonrepairable products under renewing free-replacement warranty[J].
IEEE Transactions on Reliability, 2005, 54(1): 92-97.
DOI: 10.1109/TR.2004.841723. |
| [8] |
PASCUAL R, ORTEGA J H. Optimal replacement and overhaul decisions with imperfect maintenance and warranty contracts[J].
Reliability Engineering and System Safety, 2006, 91(2): 241-248.
DOI: 10.1016/j.ress.2005.01.018. |
| [9] |
CHIEN Yuhung. Optimal age for preventive replacement under a combined fully renewable free replacement with a pro-rata warranty[J].
International Journal of Production Economics, 2010, 124(2): 198-205.
|
| [10] |
ISKANDAR B P, MURTHY D N P. Repair-Replace strategies for Two-Dimensional Warranty Policies[J].
Mathematical and Computer Modelling, 2003, 38(9): 1233-1241.
|
| [11] |
ISKANDAR B P. A new repair-replace strategy for items sold with a two-dimensional warranty[J].
Computers & Operations Research, 2005, 32(6): 669-682.
|
| [12] |
VARNOSAFADERANI S, CHUKOVA S. A two-dimensional warranty servicing strategy based on reduction in product failure intensity[J].
Computers and Mathematics with Applications, 2012, 63(2): 201-213.
|
| [13] |
SHAHANAGHI K, NOOROSSANA R, JALAIL-NAINI S G, et al. Failure modeling and optimizing preventive maintenance strategy during two-dimensional extended warranty contracts[J].
Engineering failure analysis, 2013, 28(1): 90-102.
|
| [14] |
MANNA D K, PAL S, SINHA S. A use-rate based failure model for two-dimensional warranty[J].
Computers & Industrial Engineeing, 2007, 52(3): 229-240.
|
 2016, Vol. 19
2016, Vol. 19

