2. 合肥工业大学 汽车工程技术研究院,安徽 合肥 230009
2. Automobile Engineering & Technology Research Institute, Hefei University of Technology, Hefei 230009, China
在不确定环境下,各种不确定因素(如设备磨损、模具更换、缓冲区的堵塞与饥饿)会导致复杂机械装配系统出现故障,尤其是关键设备故障会给高速运行的装配系统带来重大的经济损失[1]。为保障装配系统的连续运行,减少单台设备故障造成整个装配系统停止运行的状况,可在工作站之间增设缓冲区将设备-设备之间的“刚性连接”转变为设备-缓冲区-设备的“柔性连接”。以缓冲区库存量和设备状态为依据制定合理的维修计划,能够有效降低设备故障率并提高生产效益及装配系统的稳定性。
缓冲区库存量和设备维修时机的动态关系研究具有一定的理论难度和较高的实用价值,为此激发了一大批学者开展了这一领域的探索,并取得了许多阶段性成果。Federgruen和So[2]以设备长期运行的期望成本最小化为目标函数,确定了单台设备的最佳预防维修周期;Van der Duyn Schouten和Vanneste等[3]以串联装配系统中的单台设备为研究对象,考虑了设备失效率的变化,用嵌入法制定了以设备服务时间和缓冲库存量为基础的预防维修方法,并证明了该方法的整体最优性。Russell D Meller和David S Kim[4]建立了二级装配系统模型,利用马尔可夫链确定了最优的缓冲库存量,通过建立成本模型确定了设备的预防维修时间及维修后启动生产的时间。Kyriakidis, Dimitrakos和Karamatsoukis[5-8]等以设备状态和缓冲库存量为依据,分别考虑了设备维修方法和下级缓冲区、上级缓冲区库存量的关系,以设备运行成本最低为目标函数确定了设备修复后最优的等待时间。Yevkin和Krivtsov[9]以失效率为Weibull分布的设备为例,建立了设备的更新函数,用改进的蒙特卡洛方法求解出维修量最小的维修方法。Borrero, Akhavan-Tabatabaei[10]对设备状态的退化和缓冲库存量进行了量化,以设备长期运行的折扣成本最小化为目标函数,建立了两个不同的优化模型,制定了单台设备的最优维修方法。孟吉伟、王少华等[11]研究了缓冲库存最小安全量的计算,提出了非均匀节拍控制法,其可有效对缓冲库存进行补给。韩帮军、范秀敏等[12-13]提出了等效役龄的概念,建立了预防维修周期间故障率的递推关系式,以装配系统中的单台设备为对象建立可靠性成本模型,并用遗传算法对模型进行了优化。付芳[14]使用离散变量构建维修计划模型,设计和声搜索算法求解模型,对可行解生成过程和替换算子进行改进以保证解的多样性。通过算例验证了算法的有效性,并分别对维修间隔期、故障水平进行了敏感性分析以辅助决策。姚运志、孟晨[15]引入了关联系数以描述部件间的失效相关性,以两部件系统为例构建了系统的失效率函数,得到了复杂装备预防维修模型的解析形式。综上所述,缓冲库存量的控制对上下级设备的维修方法的制定有重要影响,目前研究大多以单台设备为对象,本文将同时考虑缓冲区和其上下级设备的约束关系,从装配系统整体的角度考虑设备运行成本和维护成本,制定具体维修方法。
本文以带有缓冲区的二级装配系统为研究对象,并将其抽象为可靠性框图模型,构建装配系统可靠性成本函数,利用马尔可夫决策理论确定装配系统中设备状态和缓冲库存的最优匹配。模型能够根据设备工作状态和缓冲库存量确定最优的维修方法并指导现场的维修调度。
1 模型表达 1.1 装配系统基本模型和状态分析以带有缓冲区的二级装配系统为研究对象,不考虑装配系统上级缓冲区的物料短缺和下级缓冲区的物料堵塞情况。装配系统中设备M1以效率d1生产工件并运送至B1储存,M2以效率d2从缓冲区B1获取工件(d1≥d2),不考虑工件在M1和B1,B1和M2之间的运送时间。详见图 1。

|
图 1 装配系统可靠性框图模型 Fig. 1 reliability block diagram model of assembly system |
随着设备M1、M2役龄的增加,其失效率也将增大,可以定期对设备状态进行检查评估并将其分为m+2个状态,以0代表设备的全新状态,无任何磨损。1, 2, …, m代表设备磨损程度逐渐增加的过程,但仍可以正常工作。m+1代表设备处于失效状态,必须进行故障维修。设备由ξ时刻的状态i转移到ξ+1时刻的状态i′的概率为pii′, 其中i′∈(i, i+1, i+2, …, m+1), 0 < pii′ < 1。
对设备可以采取的维修方式u∈{0, 1, 2},u=0代表不对设备进行维修活动,使其以现有状态继续工作,u=1代表对设备进行预防维修,u=2代表对设备进行故障维修。预防维修和故障维修的维修时间均服从几何分布,且其修复率为定值。当设备处于状态1, 2,…, m时,可以对设备采取维修方式u=0,也可以采取维修方式u=1,当设备处于状态m+1时,必须采取维修方式u=2即故障维修。
装配系统的状态由设备M1的状态i, 缓冲区B1的库存量x和设备M2的状态j决定,即
S=(i, x, j)。
其中,i∈{0, 1, 2,…, m, m+1, PM};x∈{0, 1, 2, …, K};j∈{0, 1, 2,…, m, m+1, PM}。
1.2 可靠性成本函数在构建可靠性成本模型时,将装配系统的可靠性成本归纳为任意状态下的运行成本Cij,缓冲区库存成本h*x (单位库存成本h和库存量x的乘积),预防维修成本Cp,故障维修成本Cf和停机造成的生产损失成本Cl的总和(可靠性成本函数可参考文献[5]、[7]、[8]、[13]、[19]),所以可靠性成本函数为
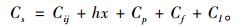
|
(1) |
当装配系统处于状态S=(i, x, j)时,如对M1进行维修需要考虑M1的停机损失成本及缓冲库存B1不能满足M2的需求而造成的生产损失,M2维修需要考虑M2的停机损失成本及缓冲库B1达到最大容量K造成的生产损失。生产损失成本等于设备单位时间生产损失量与停机时间的乘积。即生产损失成本
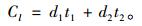
|
(2) |
其中,t1表示设备M1的停机时间;t2表示设M2的停机时间;d1、d2分别表示设备M1、M2的生产率。将式(2)代入式(1)可得
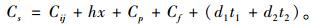
|
(3) |
设备预防维修和故障维修时间均服从几何分布,假设设备修复率为a,则修复所用时间t的概率p(t)=a(1-a)(t-1)。
2 维修方法分析令(i, x, j)∈S,Cnα(i, x, j)代表n步折扣成本的最小期望值,α为折扣因子满足0 < α < 1,折扣因子α可保证Cnα(i, x, j)在整个迭代过程中的收敛性。设备M1预防维修修成本为Cp1,修复率为a,故障维修成本Cf1,修复率为a′。设备M2预防维修成本为Cp2, 修复率为b,故障维修成本为Cf2, 修复率为b′,n=1, 2, …。结合式(1)、(2)代入式(3)中,将生产系统的运行状态进行分类,取最优成本为生产系统可靠性成本的最小值,可建立模型(4)~(6)。
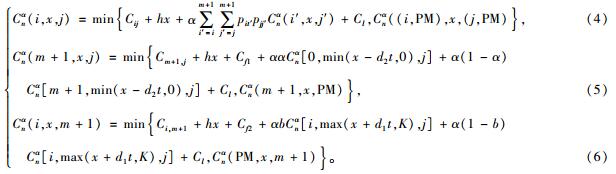
|
式(4)表示在装配系统正常运行情况下,通过选择可靠性成本的最小值判断是否对装配系统进行预防维修的方法。式(5)表示在对设备M1进行故障维修的同时,判断是否对设备M2进行预防维修。式(6)表示在对设备M2进行故障维修的同时,判断是否对设备M1进行预防维修。式(4)~(6)均满足假设:当i∈{0, 1, 2,…, m, m+1, PM}, x∈{0, 1, 2, …, K}, j∈{0, 1, 2,…, m, m+1, PM}时,初始值C0α(i, x, j)=0。
针对不同维修方法,可对式(4)~(6)展开:
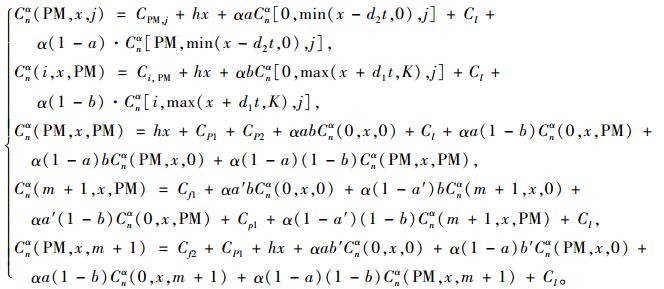
|
其中, Cnα(PM, x, j)代表对设备M1进行预防维修时n步折扣成本的最小期望值;Cnα(i, x, PM)代表对设备M2进行预防维修时n步折扣成本的最小期望值;Cnα(PM, x, PM)代表对设备M1、M2同时进行预防维修时n步折扣成本的最小期望值;Cnα(m+1, x, j)代表对设备M1进行故障维修时n步折扣成本的最小期望值;Cnα(i, x, m+1)代表对设备M2进行故障维修时n步折扣成本的最小期望值。
假设任意时刻ξ,缓冲库存量为x, 设备M1维修时间为t, 当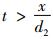
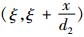
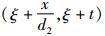
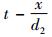
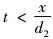
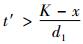
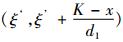
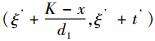
结合式(4)~(6),可得出引理1。
引理1:对任意n=0, 1, 2, …有
1) Cnα(PM, x, j)≤Cnα(m+1, x, j), 0≤x≤K, 0≤j≤m。
2) Cnα(i, x, PM)≤Cnα(i, x, m+1), 0≤x≤K, 0≤i≤m。
3) Cnα(i, x, j)≤Cnα(i+1, x, j), 0≤i≤m, 0≤x≤K, 0≤j≤m。
4) Cnα(i, x, j)≤Cnα(i, x, j+1), 0≤i≤m, 0≤x≤K, 0≤j≤m。
引理1的证明过程详见文献[7]中Lemma 1。
令Cα(i, x, j)为初始状态折扣成本的最小期望值,其中(i, x, j)∈S,因为
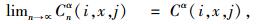
|
(7) |
且存在正数B满足:对所有(i, x, j)∈S且α∈(0, 1)有
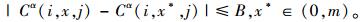
|
(8) |
证明过程详见文献[6]。
式(7)、(8)表明存在(i, x, j)∈S有常数g满足:
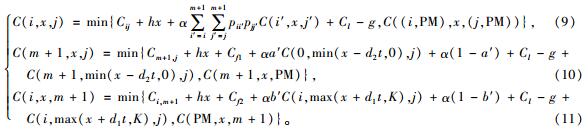
|
结合引理1中(1)~(4)和式(9)~(11)有以下结论。
即在图 1所示的装配系统可靠性模型中,设备M1存在关键状态值i*∈{0, 1, 2,…, m},有(i*, x, j)∈S满足此时对设备M1进行预防维修时的可靠性成本小于装配系统继续维持运行的可靠性成本。即(i, x, j)∈S满足
C(PM, x, j)≤C(i, x, j), 0≤i≤m, 0≤x≤K, 0≤j≤m,
C(PM, x, m+1)≤C(i, x, m+1), 0≤i≤m, 0≤x≤K。
对设备M2有相同结论,即
C(i, x, PM)≤C(i, x, j), 0≤i≤m, 0≤x≤K, 0≤j≤m,
C(m+1, x, PM)≤C(m+1, x, j), 0≤x≤K, 0≤j≤m。
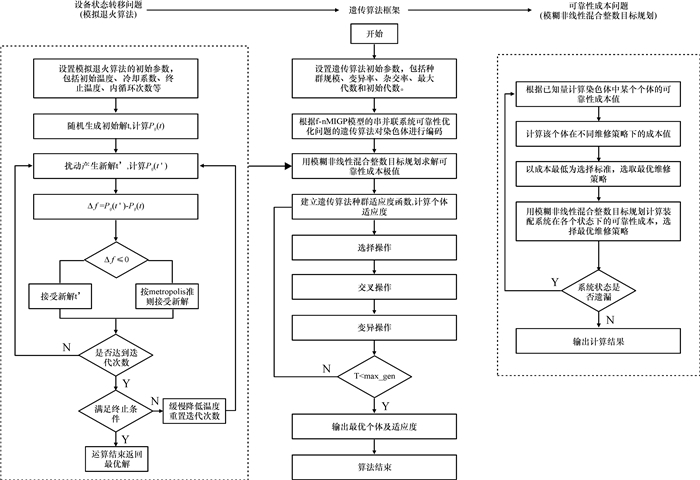
3 模型的求解该问题是由设备状态转移和维修时机选择这两个子问题组成的,关键问题是确定设备状态值i, j和缓冲库存量x之间的最佳匹配问题(即求解变量C(i, x, j)),一旦设备状态转移函数确定,那么维修时机选择问题即可转化为三参数模型求极值问题来解决。这里可以采用遗传算法作为整体框架来解决,用模拟退火遗传算法来解决Pij, 而利用模糊非线性混合整数目标规划来求解可靠性成本的最优值,整个模型的求解流程如图 2所示。
|
图 2 模型求解流程 Fig. 2 flow chart of solving the model |
从数学模型角度出发,可把模拟退火描述为:在给定领域结构后,模拟退火过程是从一个状态到另一个状态不断地随机游动。结合本文设备状态转移问题,可以用马尔科夫链描述这一过程。当设备役龄为t时,设备状态的转移概率定义为
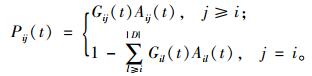
|
其中,|D|表示状态集合中状态的个数; Gij(t)称为从i到j的产生概率,其表示设备由t时刻的状态i转变为t+1时刻状态j的概率;Aij(t)为接受概率,Aij(t)表示设备从状态i转移到状态j后,接受状态j的概率。在某一温度为Tk和该优化问题的一个解xk,可以生成x′,接受x′作为下一个新解x(k+1)的概率为
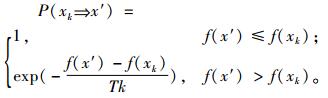
|
(12) |
式(12)中,f(x′)为状态x′的目标值;f(xk)为状态xk的目标值。
起始温度、退温操作与停止温度的确定如下。
起始温度的确定:根据初始解x0,采用2变换法随机产生下一个解x1,基于Metropolis准则的初始概率来确定,则起始温度T0=(f(x1)-f(x0))/lnpo,其中f(x0)和f(x1)表示初始个体的第一代适应度与下一代适应度的值;po为初始接受概率,且要求po∈[0.9, 0.95]。
退温操作:Te+1=a×Te,其中,e是迭代步数;a为降温系数,且a∈[0.90, 0.95]。
停止温度:采用基于不改变规则的控制法,即f(xi+1)-f(xi)=0,就可以认为达到停止温度。
3.2 最小可靠性成本问题如何将问题的解编码成为染色体是遗传算法使用中的关键问题。Gen, Ida和Kim[16]提出了一种用于解决表示为f-nMIGP模型的串并联系统可靠性优化问题的遗传算法。本文将二级装配系统看作f-nMIGP模型的串联系统的一部分,在对遗传算法进行改进的基础上提出多维参数求极值的方法。具体解决步骤如下。
Step1:设置参数和初始化。
设置种群规模(pop_size),变异率(PM),杂交率(Pc),最大代数(max_gen)和初始代数0。将(i, x, j)作为染色体,其表示设备状态值和缓冲库存量的匹配方案,最后选用矩阵的形式来表征。例如设备有6个状态值,缓冲库存量最大值为8,则可用矩阵M表示。

|
式中,i表示设备M1的状态值;x表示缓冲区库存量;j表示设备M2的状态值。矩阵M表示设备M1状态值为0时,缓冲区库存量为1且设备M2的状态值为0。同理,设备M1状态值为1时,缓冲区库存量为1且设备M2的状态值为1,以此类推,可得出整个矩阵M。
Step2:适应度函数。
对于某个个体所对应的匹配方案,要判断其优劣,一是看其是否满足设备状态转移的约束条件;二是计算其目标函数值,即各个体所对应的可靠性成本。根据该问题的特点以及初始种群的编码方式,隐含设备状态值不会主动减少以及缓冲区库存量和上下级设备的生产效率保持线性关系的约束条件。为此,需要对每个个体进行判断,看其是否满足约束条件,若不满足,则个体为不可行解;再计算其目标函数值。对于任一个体(i, x, j), 其下一状态中不可行解个数为Vn, 目标函数值为C则该个体的适应度fj为
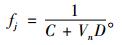
|
公式中D为定值,由决策者制定,此处令D=10。
Step3:选择操作。
选择方法组合了轮盘赌选择和最优性方法。轮盘赌选择根据每个适应值占总适应值的比例来产生下一代,最优方法为下一代保持最优染色体,克服了采样带来的随机误差。根据适应度大小对种群个体进行选择。
Step4:交叉操作。
以PC为概率进行交叉操作,采用类OX法进行交叉,具体步骤如下。
1) 随机选择一个父代交配区域如下。
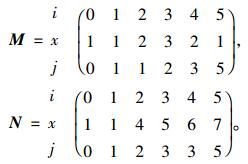
|
2) 将N中的交配区域中放在M的前面,同理也将M中的交配区域中放在N的前面,得到M′和N′。
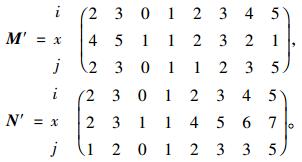
|
3) 去除原有交配位置上的片段得到第二代个体。
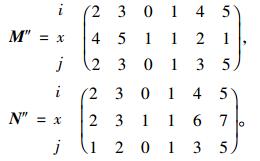
|
Step5:变异操作。
保证种群的多样性,对父代以概率PM进行变异,变异概率PM定义了执行变异操作的期望染色体数量PM×pop_size,具体变异方法如下。
随机选取若干个状态(如选取2个状态),以最大状态值5减去每个状态的值,得到一次变异结果:
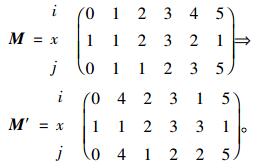
|
Step6:执行终止试验。
如果t < max_gen,返回step4操作下一代;如果t=max_gen,终止算法。
4 实例验证为了验证以上结论的正确性,现给出以下实例进行分析验证。以汽车离合器盖及压盘总成装配线中综合性能检测机和平衡机构成的装配系统为例,综合性能检测机对离合器盖及压盘总成进行综合性能检测,检测完成后半成品通过托盘运送至缓冲区B1, 等待平衡机对其进行平衡测试,详见图 3。
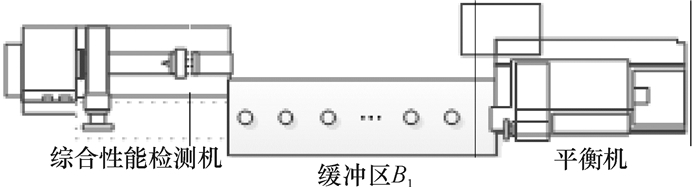
|
图 3 二级装配系统模型 Fig. 3 two-echelon assembly system model |
装配系统已知参数有
m=10, K=5, g=0, 当i, j∈(0, m)时,Cij=0.3(i+j); 当i=PM或i=m+1时,Cij=0.3j;当j=PM或j=m+1时,Cij=0.3i; CP1=1.8, a=0.98, Cf1=2.1, a′=0.95, CP2=2.1, b=0.96, Cf2=3.0, b′=0.94。
具体采用的遗传参数有:pop_size=20, max_gen=1 500.PC=0.4, PM=0.1, 把以上参数代入式(8)~(10), 在Matlab7.0环境下对模型求解,最终计算结果如表 1所示。
| 表 1 最优维修方法 Tab. 1 the optimal maintenance policy |
针对传统制造系统维修方法研究中未全面考虑系统连续性和可靠性成本的问题,提出一种带有缓冲区的复杂机械装配系统设备维修研究方法。考虑了设备状态基于役龄的随机变化,构建了基于马尔可夫理论的可靠性成本模型,并详细推导出系统在不同状态下的可靠性成本计算公式。算例分析部分以具体装配系统为例,通过改进的遗传算法求出模型最优解,即给出了具体装配系统的最优维修方法。验证结果表明装配系统维修方法是状态阈值问题。实际上,设备的维修方法可能包含各种周期性大修、小修,但基于可靠性成本的维修模型给出了维修方法的选择与缓冲库存之间的变化关系。该研究对于带有缓冲区的装配系统设备维修计划的制定具有一定的指导作用;可靠性成本模型对降低维修成本,提高装配系统的生产率和连续性有实践价值。在后续的研究工作中,将重点考虑设备失效率因子和修复率因子变化情况下的维修方法的制定。
| [1] |
QI H, ALZAABI R N, WOOD A S, et al. A fuzzy criticality assessment system of process equipment for optimised maintenance management[J].
International Journal of Computer Integrated Manufacturing, 2013, 28(1): 112-125.
|
| [2] |
FEDERGRUEN A, SO K C. Optimal maintenance policies for single-server queueing systems subject to breakdowns[J].
Operations Research, 1990, 38(2): 330-343.
DOI: 10.1287/opre.38.2.330. |
| [3] |
VAN DER DUYN SCHOUTEN F A, VANNESTE S G. Maintenance optimization of a production system with buffercapacity[J].
European Journal of Operational Research, 1991, 82(2): 323-338.
|
| [4] |
MELLER R D, KIM D S. The impact of preventive maintenance on system cost and buffer size[J].
European Journal of Operational Research, 1996, 95(3): 577-591.
DOI: 10.1016/0377-2217(95)00313-4. |
| [5] |
DIMITRAKOS T D, KYRIAKIDIS E G. A semi-Markov decision algorithm for the maintenance of a production system with buffer capacity and continuous repair times[J].
General Information, 2008, 111(2): 752-762.
|
| [6] |
KARAMATSOUKIS C C, KYRIAKIDIS E G. Optimal maintenance of a production-inventory system with idle periods[J].
European Journal of Operational Research, 2009, 196(2): 744-751.
DOI: 10.1016/j.ejor.2008.04.012. |
| [7] |
PAVITSOS A, KYRIAKIDIS E G. Markov decision models for the optimal maintenance of a production unit with an upstream buffer[J].
Computers & Operations Research, 2009, 36(6): 1993-2006.
|
| [8] |
KARAMATSOUKIS C C, KYRIAKIDIS E G. Optimal preventive maintenance of a production-inventory system when the action of "Idling" is permissible[J].
Springer Optimization & Its Applications, 2014, 91: 217-218.
|
| [9] |
YEVKIN O, KRIVTSOV V. Comparative Analysis of Optimal Maintenance Policies Under General Repair With Underlying Weibull Distributions[J].
IEEE Transactions on Reliability, 2013, 62(1): 82-91.
DOI: 10.1109/TR.2013.2241196. |
| [10] |
BORRERO J S, AKHAVAN-TABATABAEI R. Time and inventory dependent optimal maintenance policies for single machine workstations: An MDP approach[J].
European Journal of Operational Research, 2013, 228(3): 545-555.
DOI: 10.1016/j.ejor.2013.02.011. |
| [11] |
孟吉伟, 王少华, 李小龙. 串行连续生产线的缓冲库存控制与可靠性研究[J].
机械设计与制造, 2012(5): 6-8.
MENG Jiwei, WANG Shaohua, LI Xiaolong. Buffer stock control and reliability of serial continuous production line[J]. Machinery Design & Manufacture, 2012(5): 6-8. |
| [12] |
韩帮军, 范秀敏, 马登哲. 基于可靠度约束的预防性维修策略的优化研究[J].
机械工程学报, 2003, 39(6): 102-105.
HAN Bangjun, FAN Xiumin, MA Dengzhe. Research on the optimal preventive maintenance policy based on reliability constraints[J]. Chinese Journal of Mechanical Engineering, 2003, 39(6): 102-105. |
| [13] |
韩帮军, 范秀敏, 马登哲. 用遗传算法优化制造设备的预防性维修周期模型[J].
计算机集成制造系统, 2003, 9(3): 206-209.
HAN Bangjun, FAN Xiumin, MA Dengzhe. Optimization of equipment preventive maintenance cycle in production system based on genetic algorithm[J]. Computer Intergrated Manufactueing Systems, 2003, 9(3): 206-209. |
| [14] |
付芳. 基于可靠性的机电设备维修计划优化[J].
计算机集成制造系统, 2013, 19(12): 2940-2946.
FU Fang. Maintenance scheduling optimization for electromechanical equipment based on reliability[J]. Computer Intergrated Manufactueing Systems, 2013, 19(12): 2940-2946. |
| [15] |
姚运志, 孟晨, 王成. 考虑失效相关的多部件系统最优预防维修策略[J].
计算机集成制造系统, 2013, 19(12): 2976-2981.
YAO Yunzhi, MENG Chen, WANG Cheng. Optimal preventive maintenance policies for multi- unit system considering failure interactions[J]. Computer Intergrated Manufactueing Systems, 2013, 19(12): 2976-2981. |
| [16] |
GEN M, IDA K, KIM J. System reliability optimization with fuzzy goals using genetic algorithm[J].
Japanese Journal of Fuzzy Theory anti Systems, 1998, 10(2): 356-365.
DOI: 10.3156/jfuzzy.10.2_176. |
 2016, Vol. 19
2016, Vol. 19
