随着科学技术的迅速发展,由不同类型多台设备组成的混联系统得到了广泛的应用。相比较单台设备的维护优化,多设备混联系统维护优化调度无论从策略的决策约束考虑、整体优化目标,还是设备相关分析、动态优化流程都更为复杂,需要作为系统工程开展深入研究,为企业管理层提供亟需的多设备维护优化调度的策略和方法[1]。在混联系统中,如果各台设备不存在任何依赖性,说明每个设备是相互独立的,对每台设备各自维护建模,并分别输出最优维护周期[2-3]。但在实际生产中,系统中各设备间存在密切的依赖性,在维护调度优化过程中,不仅需要考虑每台设备自身的健康衰退特征,同样应当综合分析其他关联设备的维护信息。比如说,当系统中某设备发生故障,需要采取维护活动时,系统就停机;在这个过程中,对系统中的剩余设备也采取相应的维护活动,虽然它们可能没有发生故障,或者没有达到它们的维护时刻。
目前,系统维护优化调度策略主要有成组维护的优化调度策略[4-5],比如Lira等[5]针对成组维护中的信息和通讯技术进行了研究,论证了其在成组维护结果中发挥着重要作用;机会维护的优化调度策略[6-7],比如Ding等[6]研究了风电涡轮机中部件间的经济依赖性,利用事后维护和预防维护产生的维护机会对多台涡轮机进行维护作业,通过仿真方法评估所提出的机会维护策略;批量更换的优化调度策略[8-9],比如Scarf等[8]提出了一种改进型批量更换的优化调度策略,在策略中综合应用了混合批量更换、基于役龄的检测和机会组合方法;考虑系统劣化的优化调度策略[10-13],比如刘繁茂等[10]对一般混联的多设备维护决策的问题进行了研究,利用马尔可夫链的思想,建立了系统的视情维修策略,Yang[12]、Noureifath等[13]对并联的多设备系统进行了维护决策建模,分析了并联系统的维护策略。上述各种多设备混联系统维护优化策略,无论是成组维护、机会维护、批量更换,还是考虑劣化的优化调度策略,都会受到状态信息和设备衰退的制约。目前的设备维护优化调度的模型中,假设维护可以让设备修复到原始的最佳状态。而实际情况并不能修复如新,仅仅获得了状态的部分优化。另外,文献中的系统维护优化调度策略都假设设备的维护周期是已知量或者维护周期是固定不变的,没考虑系统发生停机时多设备间的相关性。
针对以上问题,考虑多设备混联系统的结构、动态维护调度等难点,综合分析了设备自身的健康衰退过程和系统不同结构配置的影响作用,以系统的维护资源为约束条件,提出了多阶段维护优化调度模型。维护调度策略在每一次维护活动中对性能衰退到一定程度的设备尽量多地进行维护,缩短了系统在生产过程中的停机时间,减少对系统维护人员的调度次数。同时,在系统的维护过程中,由于受成本的限制,维护资源不可能无限地满足系统维护的需求,有时不可能同时进行多个维护动作,维护调度策略考虑了多个维护动作的合理优化,帮助企业管理层动态高效地制定面向整个系统的维护调度优化方案。
1 问题域描述对于多设备混联系统的维护调度,通过故障阈值确定设备采取的维护动作方式,即当设备故障率达到某一个阈值时,就会相应地触发设备的维护活动。如系统中某一台设备的故障率达到了小修的阈值,则需要对设备进行小修维护;某一台设备的故障率达到了大修的阈值,则需要对设备进行大修维护;某一台设备的故障率达到了更换阈值,则需要对设备进行更换维护。
系统性能衰退是采取维护策略的基础,系统性能衰退的正确性影响到采取的维护动作方式,进而影响到设备的维护效果。用系统的故障率(failure rate, FR)来表示系统的性能状态,FR越大,代表系统的衰退状态越严重,系统发生故障的几率增大。对于设备的故障率分析,针对不同类型的设备,由大量的故障历史数据的统计分析可知,一般设备的故障率都呈现“浴盆曲线”的分布形状。因此,文中故障率分布采用威布尔分布来表示:

|
(1) |
其中,β为形状参数,η为尺度参数,β>0,η>0,t代表时刻。
根据可靠性理论,对威布尔故障分布进行分析,在η保持不变的情况下,如果β < 1,说明设备的故障率为下降趋势;如果β=1,说明设备的故障率保持不变,为一个常数;如果β>1,则设备的故障率将呈现递增的趋势。这说明威布尔分布针对不同的参数取值,都可以精确实现对设备故障率曲线的描述。对于威布尔参数(β, η)的值,可以通过对设备的故障历史数据进行统计分析得到。设备运转过程中的故障率随着设备运行时间的增加逐渐升高。因此,为了延长设备的使用时间和设备的寿命,要在设备出现故障之前对设备采取维护措施。
为了减缓设备性能的退化,需要采取各种的维护动作。对于不同的设备退化状态,采取不同的维护动作,可以将设备状态优化至不同的目标值,对设备产生不同的维护效果。具体的维护动作如下。
1) 小修:对设备采取有限的维护工作,也就是对设备进行保养维护。目的是让设备尽可能地保持在当前的健康状态。用RM表示对部件进行小修的故障率阈值。
2) 大修:对设备采取较为充分的维修工作,修复部分损耗。目的就是让设备从当前健康状态恢复到一个更好的健康状态,使设备的衰退状态得到显著改善。用RI表示对部件进行大修的故障率阈值。
3) 更换:对设备进行更换,直接用新的零部件更换发生故障或者损耗的零部件。在这种情况下,设备将恢复到初始健康状态,使衰退的设备恢复到全新状态。用RR表示对部件进行更换的故障率阈值。
根据RM,RI,RR这3种维护阈值,可以确定设备采取的维护动作方式。设备在运转过程中,当某一设备的故障率达到维护阈值时,例如达到大修的维护阈值,为了降低设备的维护时间和提高设备整体利用率,对于其他设备,如果也达到了维护阈值,则对这些设备也要采取维护动作,也就是连带维护。根据威布尔分布确定设备的故障率,对设备采取相应的维护措施。
2 算法设计对于系统的维护优化,当每一次的维护活动发生时,都会产生很多次的小修、大修和更换。因此,对于系统的总成本,包括系统的维护成本Cm、故障成本Cf和资源成本Cr。同时,在考虑系统利用率的基础上,将维护动作引起的停机成本Cd也集成到总成本。因此,综合考虑成本和利用率对系统采取一次维护活动的成本模型为
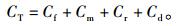
|
(2) |
在式(2)中,一次维护活动的系统故障成本模型表示为

|
(3) |
式中,FF表示系统的故障独立成本,FR(i, t)表示设备i在维护时刻t的故障率;Fi是设备的故障依赖成本,与维护动作无关;n表示设备的数量。
一次维护活动的系统维护成本模型表示为

|
(4) |
式中,CM, m,CI, m,CR, m分别表示设备i的小修、大修和更换维护成本;FM表示系统的维护独立成本,与维护动作无关;XM, i, t,XI, i, t,XR, i, t分别表示在时刻t对设备i是否进行小修、大修和更换,如果进行,则3个参数值分别为1,否则,为0;MM, i,MI, i,MR, i分别表示设备i的小修、大修和更换的维护依赖成本。
一次维护活动的资源成本模型可以表示为
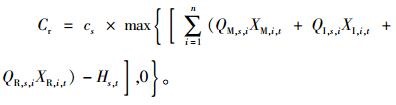
|
(5) |
式中,Cr表示备件缺货成本。cs表示进行维护时缺少所需要备件的惩罚系数,QM, s, i,QI, s, i,QR, s, i分别表示对设备i进行小修、大修和更换所需要的备件s的数量,Hs, t表示在时刻t具有的备件s的数量。
当某维修时刻缺少备件时,则需要进行订货。在式(5)中,Hs, t等于t-1时刻的可用备件数量与t时刻到达或者释放的备件数量减去t-1时刻所需要的备件数量。因此,Hs, t表示为
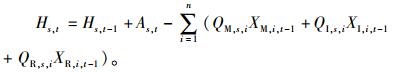
|
(6) |
式中,Hs, t-1表示在时刻t-1具有的备件s的数量,As, t表示在时刻t到达或者释放的可用备件s的数量。
一次维护活动的系统停机成本模型表示为
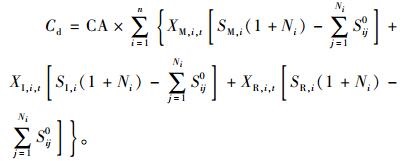
|
(7) |
式中,CA表示系统单位时间的停机成本,SM, i,SI, i,SR, i分别表示设备i的小修、大修和更换的维护时间;Ni表示系统的预计停机数,即设备i停机维修时,所导致的其他停机设备的数量,当确定设备i的预计停机数时,假设其他设备状态是良好的;Sij0表示第i个设备和第j个设备同时维护所节约的时间。
基于式(3)~(7),就可以根据式(2)获得对系统进行一次维护活动的总成本模型CT。实际上,系统从初始的健康状态开始运转,在运转过程中,如果某一设备的故障率达到或者超过维护阈值,则会给该设备触发一次维护活动。设备维护后,性能会得到恢复,在后续的使用过程中,故障率不断提高,直到设备故障率又达到维护阈值,则会给该设备触发二次维护。以此类推,直到设备的全寿命周期终止。因此,在每一次维护活动费用的基础上,也要考虑在整个生命周期内的多阶段维护优化的总费用,系统总费用率表示为

|
(8) |
式中,CTotal表示系统维护优化的总费用率,Cj, T表示系统进行第j次维护活动所产生的总费用, T表示维护周期,D表示系统的全寿命周期。m表示系统在全寿命周期内所执行的维护活动的总次数,Cq表示系统在执行一次维护活动时所产生的启动费用。
为了让整个系统的全生命周期的总费用率最小,不但要考虑系统在执行每一次维护时所产的故障费用、维护费用、资源费用和停机损失,还要考虑系统在全生命周期内的维护活动的次数要尽量少。满足这两个目标,系统的总费用率才会降低。因此,系统的全生命周期的总费用率具有全局性的特点。
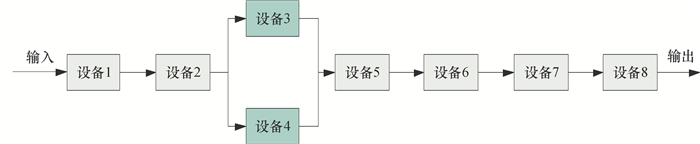
3 实例分析在实例分析中,以液压泵系统为研究对象。假设液压泵的运转是8台设备相互协作完成的。因此,对液压泵进行维护优化,就是对8台设备进行维护优化。另外,在运行过程中,随着时间的增加,液压泵的性能会逐渐衰退,健康状态会逐渐变差。因而需要对液压泵进行相应的维护使其维持正常的工作,避免液压泵失效带来的高成本和高风险。并且,随着液压泵使用运行成本和维护成本的不断增加,也可以考虑实施置换维护。因此,维护优化以每阶段的维护优化费用和总的费用率为目标,制定维护策略。液压泵的8台设备的相关关系如图 1所示。本算例应用遗传算法进行求解,数据分析所用运行平台为Matlab、VC,运行环境为Windows XP。
|
图 1 系统的设备拓扑结构图 Fig. 1 The basic structure of pumps |
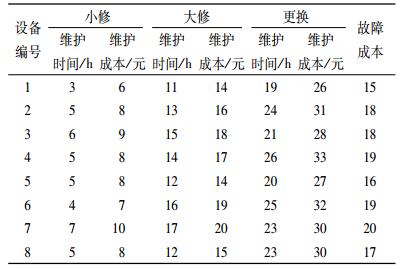
维护分为3种维护方式:小修、大修和更换。针对不同的设备,不同的维护动作对应的维护时间和成本是不同的。但是对于设备的故障成本,是与设备的维护动作不相关的,是由不同的设备决定。因此,对不同设备的故障成本及不同维护动作的维护时间和成本见表 1。
| 表 1 部件故障成本和维护动作时间及成本 Tab. 1 Failure cost, maintenance action time and cost |
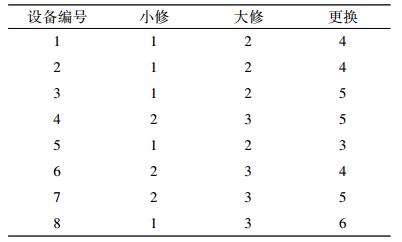
不同设备的不同维护动作对应的威布尔尺度参数和形状参数是不一样的,如表 2所示。
| 表 2 设备维护动作的威布尔参数表 Tab. 2 Weibull parameters of maintenance actions |
在液压泵的维护优化中,主要考虑设备的备件这种维护资源。在案例分析中,备件总数量为14。表 3给出了每台设备小修、大修和更换所需要的备件资源的数量。
| 表 3 不同维护动作的备件资源数量 Tab. 3 Spare parts demand for maintenance actions |
| 表 4 预计停机数的取值 Tab. 4 The number of expected downtime |
除了上述的模型输入参数,模型中的其他输入参数见表 5。
| 表 5 其他参数的取值 Tab. 5 Other parameters |
遗传算法(genetic algorithm, GA)是模拟生物进化过程而进行的一种多参数、多群体同时优化的方法,并行性和解空间的全局搜索是其最大的特征。GA主要是由选择(selection)、交叉(crossover)和变异(mutation)3种基本运算构成。首先把问题的解空间映射为编码空间,产生初始种群开始其搜索。其次,用模型的适应度衡量染色体的优劣。通过选择、交叉和变异的运算,生成下一代染色体。最后,在新的群体中,凭借模型适应度的优劣选择部分后代,淘汰部分后代,保持了种群的优越性和数量的限制。
在模型优化求解过程中,采用遗传算法进行优化,主要步骤为:1)编码部件的维护顺序,并产生初始种群;2)计算父代的个体适应度值,进行选择、交叉和变异操作,计算子代个体适应度值;3)用子代替代父代,继续进行遗传操作,直到达到最大进化代数;4)对优化结果进行统计,设备结束一次维护活动;5)判断当前时间是否已到达设备总运行时间,如果没有到达,对设备继续进行检测是否有突发问题产生,如果有问题产生,则动态刷新资源库,如果检测部件的故障率达到维护阈值,就产生第2次维护活动,继续采用遗传算法进行模型的优化,重复这个过程,直到设备达到总的运行时间。
另外,对于遗传算法的参数设定为:编码采用部件的编号进行实数编码,以设备维护优化的总费用率为适应度函数,进化种群为30,最大遗传代数为300,选择概率为0.8,交叉概率为0.8,变异概率为0.1。
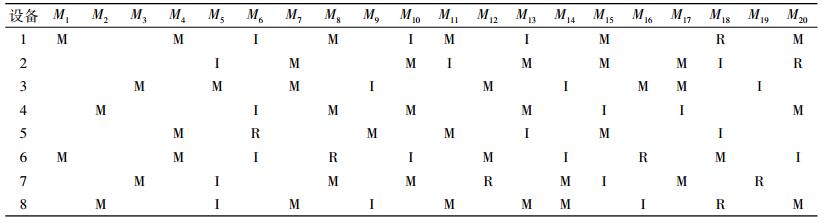
3.3 维护优化分析首先,选择常见的周期维护优化作为参考策略。将系统的整个生命周期划分为20个维护周期(T=20),时间单位为d。根据每台设备的故障率,计算得出在周期维护下,每个设备的优化情况,见表 6。
| 表 6 周期维护优化模型的维护优化表 Tab. 6 Maintenance scheduling of periodic maintenance |
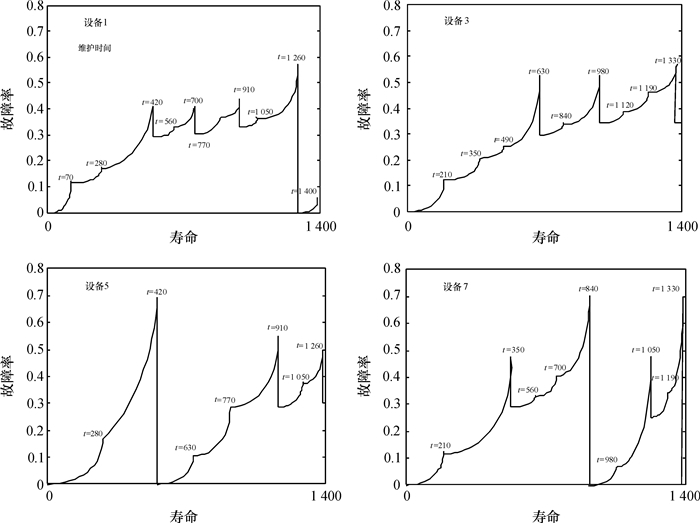
图 2所示的是4台设备的周期维护优化情况以及这4台设备的故障率变化情况。可以看出,设备的故障率发展趋势是不一样的,这是因为每个设备自身的性能衰退是不同的,以及采取周期维护后,随着维护次数的不同,设备的故障率也会随之发生变化。
|
图 2 周期维护优化模型故障率(t表示时刻) Fig. 2 Failure probability of periodic maintenance scheduling model |
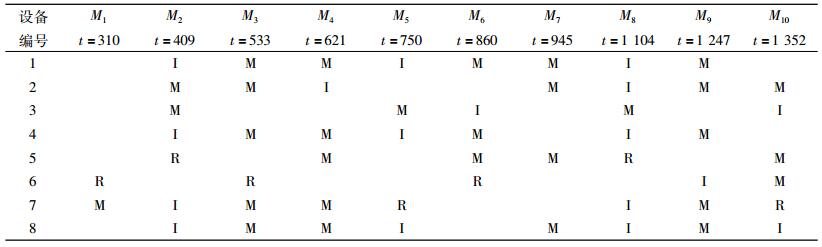
根据式(2)和(8),可以计算每台设备的维护优化情况。在系统的整个生命周期内,系统总共进行了10次维护活动,对于每台设备在这10次维护活动进行的维护优化见表 7。
| 表 7 维护优化模型的维护表 Tab. 7 Maintenance scheduling of proposed maintenance scheduling model |
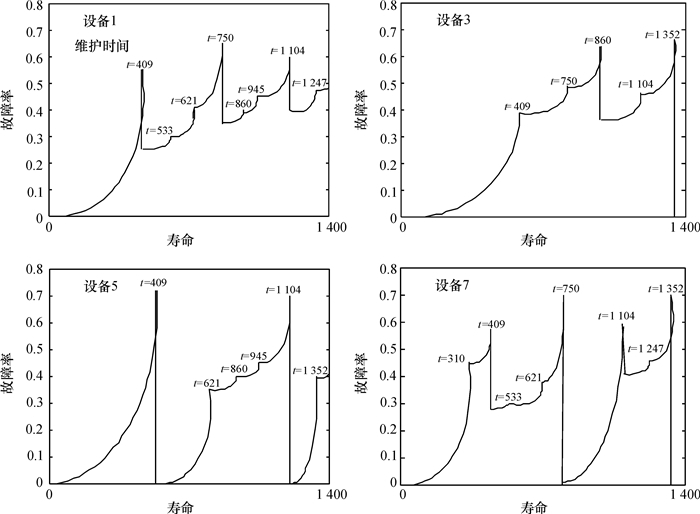
对应图 2中的4台设备的故障率变化情况,图 3所示的是基于提出的维护优化模型系统中这4台设备在整个生命周期内的维护情况和故障率变化情况。从图 3可以看出,在设备的运转过程中,每台设备的故障率的发展趋势是不同的,除了设备自身的性能衰退有关外,还与设备采取的维护策略有关,从而造成了每台设备的故障率趋势的差异。在提出的模型基础上,对设备进行有效的维护,可以保持设备的故障率在一个较低的水平,进而可以保证设备在长时间内稳定工作。
|
图 3 维护优化模型故障率(t表示时刻) Fig. 3 Failure probability of proposed maintenance scheduling model |
为了说明遗传算法的有效性,以及设备维护费用的变化情况,图 4显示了设备第2次维护活动时,维护费用的变化情况。随着遗传算法迭代次数的增多,设备的维护费用逐渐降低,最后收敛在一个稳定的水平,得到整个设备维护费用的最优值,充分验证了遗传算法在优化过程中的有效性。
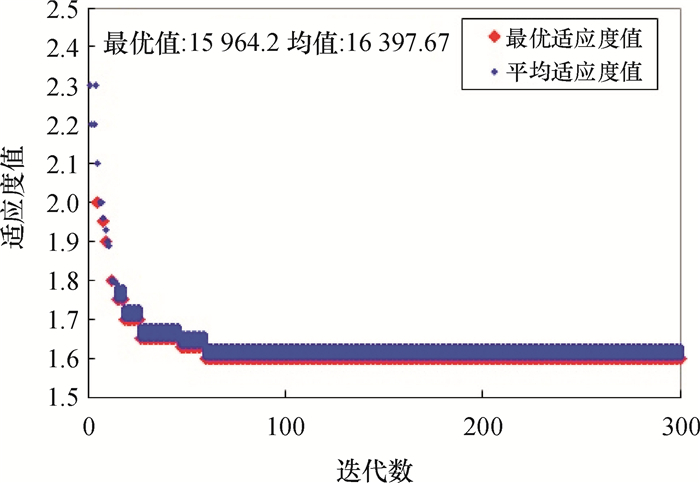
|
图 4 设备第2次维护活动的费用变化趋势图 Fig. 4 Cost changing trend of the second maintenance activity |
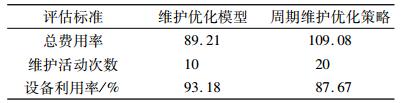
对于以上2种维护优化模型的分析见表 8。虽然周期维护优化策略通过采取不同的维护动作提高了设备的利用率,但是在设备维护优化过程中,采取的维护活动次数较多,造成了设备停机时间过长,进而损耗了高昂的设备维护成本。多设备混联系统的维护优化策略不仅仅降低了设备维护优化的总费用率,还提高了设备的利用率。并且,维护活动次数较少,从而降低了设备的停机时间。因此,在设备的总费用率、维护活动次数和设备利用率方面,维护优化策略都明显优于周期维护优化策略。
| 表 8 不同维护优化策略的结果比较 Tab. 8 Results comparison for different maintenance scheduling strategies |
本文主要介绍了多设备混联系统的维护优化策略,考虑了系统的性能衰退和结构相关性、设备间的相关关系、维护资源的约束,建立了多设备系统的维护优化模型。将模型应用到液压泵系统中,以周期性维护优化策略为参照策略,通过对模型的比较分析,维护优化策略在总费用率、维护活动次数和利用率等方面都优于周期性维护优化策略。并且,随着对设备维护次数的增多,维护效果会逐渐降低,更加符合设备的实际情况。
| [1] |
奚立峰, 周晓军, 李杰. 有限区间内设备顺序预防性维护策略研究[J].
计算机集成制造系统, 2005, 11(10): 1465-1468.
XI Lifeng, ZHOU Xiaojun, LI Jie. Research on sequential preventive maintenance policy in finite time horizon[J]. Computer Integrated Manufacturing Systems, 2005, 11(10): 1465-1468. |
| [2] |
周晓军, 沈炜冰, 奚立峰, 等. 一种考虑修复非新的多设备串行系统机会维护动态决策模型[J].
上海交通大学学报, 2007, 41(5): 106-11.
ZHOU Xiaojun, SHEN Weibing, XI Lifeng, et al. A dynamic opportunistic preventive maintenance model for a multi-unit series system with consideration of imperfect maintenance effect[J]. Journal of ShangHai JiaoTong University, 2007, 41(5): 106-11. |
| [3] |
宓乐英, 吕柏荣. 多设备串行系统预防性维护的动态决策优化研究[J].
机械设计与研究, 2008, 35(11): 8-10.
MI Leying, LU Borong. Research on dynamic preventive maintenance optimization for multi-unit series systems[J]. Journal of Machine Design and Research, 2008, 35(11): 8-10. |
| [4] |
杨元, 黎放, 侯重远, 等. 基于相关性的多部件系统机会成组维修优化[J].
计算机集成制造系统, 2012, 18(4): 827-832.
YANG Yuan, LI Fang, HOU Zhongyuan, et al. Opportunistic group maintenance optimizeion of multi-unit system inder depedndence[J]. Computer Integrated Manufacturing Systems, 2012, 18(4): 827-832. |
| [5] |
LIRA E M, RIPOLL P, PEIRO J M, et al. The role of information and communication technologies in the ralationship between group potency and group maintenance outcomes: a longitudinal study[J].
Behaviour & Information Technology, 2013, 32(2): 147-155.
|
| [6] |
DING F, TIAN Z. Opportunistic maintenance for wind farms considering multi-level imperfect mainteance thresholds[J].
Renewable Energy, 2012, 45: 175-182.
DOI: 10.1016/j.renene.2012.02.030. |
| [7] |
TAGHIPOUR S, BANJEVIC D. Optimum inspection interval for a system under periodic and opportunistic inspections[J].
IIE Transactions, 2012, 44(11): 932-948.
DOI: 10.1080/0740817X.2011.618176. |
| [8] |
SCARF P A, CAVALCANTE C A V. Hybrid block replacement and inspection policies for a multi-component stsem with heterogeneous component livies[J].
European Journal of Operational Research, 2010, 206(2): 384-394.
DOI: 10.1016/j.ejor.2010.02.024. |
| [9] |
SHEU S H, CHEN Y L, CHANG C C, et al. A block replacement policy for systems subject to non-homogeneous pure birth shocks[J].
IEEE Transactions on Reliability, 2012, 61(3): 741-748.
DOI: 10.1109/TR.2012.2206270. |
| [10] |
刘繁茂, 朱海平, 邵新宇, 等. 一种基于马尔可夫链的多设备串并联系统视情机会维修策略[J].
中国机械工程, 2009, 20(7): 851-855.
LIU F M, ZHU H P, SHAO X Y, et al. A condition-based opportunistic maintenance strategies for multi-unit series and parallel system based on markov chain[J]. China Mechanical Engineering, 2009, 20(7): 851-855. |
| [11] |
GHARBI A, KENNE J P. Maintenance scheduling and production control of multiple-machine manufacturing systems[J].
Computers & Industrial Engineering, 2005, 48(4): 693-707.
|
| [12] |
YANG S J. Unrelated parallel-machine scheduling with deterioration effects and deteriorating multi-maintenance activities for minimizing the total completion time[J].
Applied Mathematical Modelling, 2013, 37(5): 2995-3005.
DOI: 10.1016/j.apm.2012.07.029. |
| [13] |
NOUREIFATH M, CHATELET E. Integrating production, inventory and maintenance planning for a parallel system with dependent components[J].
Reliability Engineering and System Safety, 2012, 101: 59-66.
DOI: 10.1016/j.ress.2012.02.001. |
 2016, Vol. 19
2016, Vol. 19