2. 南京航空航天大学 理学院,江苏 南京 210016
2. College of Science, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
在供应链系统中存在的干扰因素容易给供应链运作带来风险和损失。近年来,一种供应链弹性管理(supply chain resilient management,SCREM)模式开始得到了重视[1-3]。SCREM通过快速处理供应链运作中的各种干扰信息,帮助系统恢复到原有状态或者建立一个新状态,使得系统经历干扰以后显得更有竞争优势[4-5]。随着供应链网络和网络设计的出现,一些学者也发现了其中存在干扰和不确定因素,弹性管理证实其可以降低供应网络的脆性[6-8]。文献[9]分析了全球供应链选址问题中的脆性因素,提出了一组结合危险因素(如:货物迟交, 汇率, 质量问题, 物流运输等故障, 生产风险)的供应链网络问题多阶段模型。文献[10]提出了一系列脆性定义及其特性,提供了相应的策略列表及其风险保障方法。文献[11]将供应链脆性研究的现有文献与风险管理行业从业人员的探索性访谈结果做比较,研究了供应链未来的发展趋势。文献[12]探讨了随机需求、随机仓库容量和点对点的交易过程,给出几种随机规划模型以便处理可选择的弹性问题。文献[13]通过一种模糊数学规划方法实现了一种弹性供应链网络架构。
然而,以上干扰环境下的弹性研究主要存在以下几个问题:1)缺乏全面的弹性管理理论框架;2)缺乏基于弹性管理理论下的供应链网络设计研究;3)缺乏基于弹性管理的模型;4)缺少干扰损失评估,极少研究系统的稳定性和绩效量化评估。文献[14]考虑了面对干扰风险时保护零部件供应商和订单数量分配的最佳选择,提出了一种不同风险偏好时的混合规划方法。然而其模型只是针对单个供应方的风险管理问题,未深入探讨脆性因素对供应链系统多个成员的优化决策问题。文献[15]通过优化库存分配和运输路径设计了一个可重构供应链网络,提出了两阶段最短路径优化问题,但研究中并未对风险管理做出进一步的量化分析。
因此,本文将在上述研究的基础上,研究基于弹性管理下的供应链网络设计问题,分析集弹性制造定价/弹性空库存惩罚/弹性预警/弹性成员选择/弹性拥堵延迟/弹性运输于一体的系统供应架构,提出客户最低期望容忍水平,建立基于弹性管理下的数学模型,用多个指标对系统稳定性和绩效进行量化评估。最后,通过仿真案例进行对比和分析,验证模型的弹性架构和经济价值。
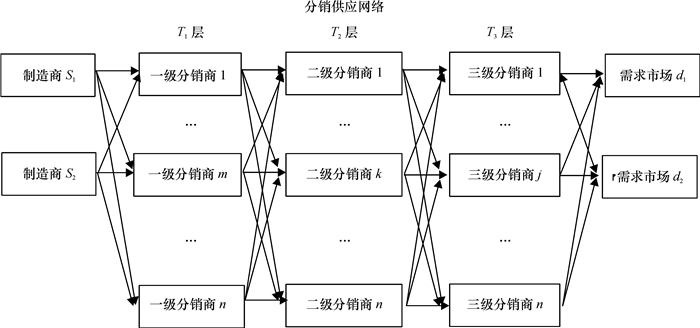
1 网络结构简化正向供应网络,如图 1所示,假设正向供应只有2个竞争型制造商S1和S2。分销供应网络有n个一级、二级和三级分销商,组成1个3层正向供应网络,层级用Ti表示,i∈{1, 2, 3},末端有2个需求市场。
|
图 1 弹性网络结构图 Fig. 1 Resilient network structure |
处于竞争中的2个制造商根据需求市场信息制定生产计划,以一定的成本提供产品给分销供应网络,分销供应网络通过一级分销商、二级分销商和三级分销商依次逐层配送产品,分销网络中的每个节点都有最大库存限制,如果没有达到最大库存,会有空库存惩罚,并且产品检测和封装成本忽略不计。
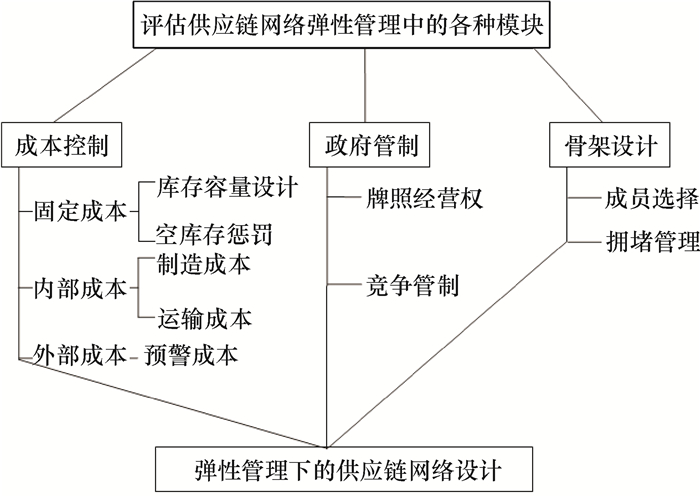
在各种不确定条件和节点失效的环境中,供应链设计被认为是增强系统弹性,降低系统脆性的一个重要因素[2, 5]。这里有必要对网络设计中的弹性模块进行评估,具体见图 2。
|
图 2 供应链网络弹性评估 Fig. 2 Resiliency assessment of supply chain network |
从图 2看出,基于弹性管理下的供应链网络设计模块一般包括成本控制模块(cost control)、政府宏观控制模块和骨架设计模块。成本控制包括固定成本、内部成本和外部成本,是对系统各种成本的核算与控制。其中,固定成本包括库存容量设计和空库存惩罚, 内部成本包括制造成本和运输成本,外部成本包括预警成本;政府宏观控制模块包括牌照经营权管理和寡头垄断控制,是政府为了公众利益与社会福利的一种宏观调控;骨架设计模块包括网络成员选择和道路拥堵管理,根据节点的有效性对网络架构进行动态调整。
目前关于供应链风险方面的研究,一方面有供应链应急管理,强调的是未知扰动发生后,对整个系统的补救措施和方法;另一方面有供应链干扰管理,是在不推翻所有原方案的前提下,局部调整部分现有系统资源,来恢复系统运作,使得未知扰动对原系统的冲击最小。在此提出了供应链弹性管理的思想,并将其运用到供应链网络设计中,建立一种弹性网络运作模型。
2 基于弹性管理的竞争型多源分销网络模型 2.1 模型的假设1) 网络线路是规则的,上下级点与点之间是可达的。物流过程中不存在不规则的、不可达的现象。
2) 分销网络中每个节点都有各自的库存容量,通过量过大会出现拥堵现象,通过量过小会有空库存惩罚。
3) 分销过程中考虑制造成本、运输成本和预警成本,产品检测、封装成本和其他成本忽略不计。
4) 分销网络中每个节点都有在一定程度上进行风险管理、弹性运作的能力。
5) 进入行业的经营权受到政府的牌照经营权管制,政府同时还会进行寡头垄断监管。
2.2 模型的符号说明RN为弹性网络;
Di为第i个市场的产品需求量(i=1, 2);
Xa为任意2个节点运输线路(简称供应弧a)上的物流量, X为常规物流量F或者期望物流量E;
Node为分销供应网络中的节点;
M和m同为常数,为供应弧或者节点的限制参数;
CapNode为分销供应网络中的节点库存最大容量;
Ii为第i层分销网络的供应弧输入(i=T1, T2, T3);
Oi为第i层弹性网络的供应弧输出(i=S1, S2, T1, T2, T3);

|
显然,传统的一般网络只考虑了整个系统的成本效用函数,而忽略了各级分销商失效的问题,上一级分销商的失效,可能会影响下一级分销商、制造商和需求市场的运作,也可能会导致整个系统的中断,给系统带来巨大损失。因此,在这里有必要将供应链弹性管理的思想考虑进来,设计一种弹性供应网络。弹性供应网络中的各级企业节点越来越认识到节点连接稳定性对于网络设计和制定生产计划有着越来越重要的现实意义。
在此结合供应链弹性管理的思想,在设计竞争型弹性分销供应网络时,既希望各级分销商的弹性最好且满足一定程度的稳定性,同时也希望系统的成本效用最小。在考虑了各级分销商的容忍服务水平,选择自己信赖并且相对可靠的分销商之后,设计了一种多级多源供应的正向节点选择,在兼顾系统稳定性的同时,达到系统成本最小化。干扰环境下,弹性网络供应应该考虑多源供应的约束,这里多源系数ρ和可靠性水平Pv的定义如下:
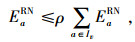
|
(1) |
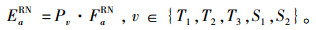
|
(2) |
1) 弹性制造定价成本。
单价弹性制造成本Ps1RN=Ps2RN=
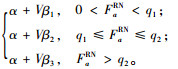
其中, a∈IT1,α为市场基数,Vβ1,Vβ2和Vβ3为弹性价格因子,Vβ1>Vβ2>Vβ3, q1和q2为常数。
制造成本效用
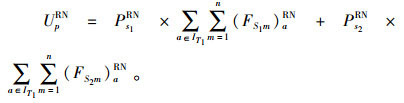
|
(3) |
(2) 弹性库存(空)惩罚成本。
假设EmptyNodeRN=CapNodeRN-FNodeRN,CapNodeRN为分销网络中的节点库存容量, 当通过节点的物流总量FNodeRN小于CapNodeRN时会有库存为空的成本惩罚,弹性管理网络中节点中库存有冗余容量的惩罚成本UvNodeRN为
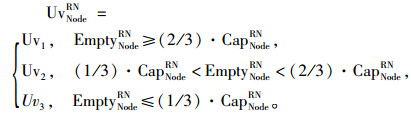
|
其中, Uv1,Uv2和Uv3为常数(Uv1>Uv2>Uv3),
库存(空)惩罚成本效用
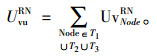
|
(4) |
3) 弹性预警成本
假设pvNodeRN为分销网络节点分销商可靠性系数,pvNodeRN根据节点所在地理区域(西部地区、中部地区和沿海地区)而发生变化。apv为基础可靠性系数,bpv1,bpv2和bpv3为弹性冗余可靠性系数,bpv1 < bpv2 < bpv3, Cpv为预警成本基数,ENodeRN为节点的期望总物流量,
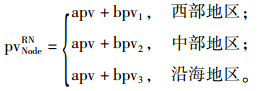
|

|
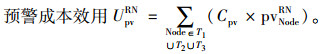
|
(5) |
4) 弹性拥堵延迟。
弹性拥堵延迟LNodeRN=
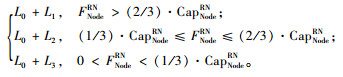
其中, L1>L2>L3, L0为基础延迟,L1,L2和L3为拥堵延迟。
(UL)NodeRN=A+B×YYNodeRN×LNodeRN, 其中A和B为常数;
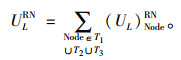
|
(6) |
存在纵向服务时限因子max[(LT1)NodeRN]+max[(LT2)NodeRN]+max[(LT3)NodeRN] < L′, L′为常数。
5) 弹性运输成本。
假设CTA和CTB为路况牵引因子,分销网络供应弧运输成本CTaRN=CTA+CTB×LNodeRN,需求市场供应弧运输成本为(CTA)aRN=CTA。
弹性管理网络总运输成本
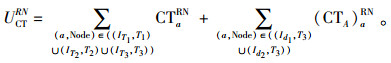
|
(7) |
6) 弹性成员选择。
考虑了三级分销网络的各级分销商的期望容忍水平。其中,u、u1和u2分别为一级分销商、二级分销商和三级分销商对外界需求的容忍最低满足率。当分销商运作失效时,流入的期望流量要大于或者等于需求的一定倍数,才能基本满足或者超过这个最低层次的服务水平,有约束:
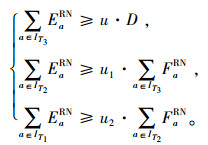
|
(8) |
为了简化计算,只考虑第一个约束,忽略后面2个期望容忍水平的约束。综上所述,则弹性管理网络的总设计成本效用:
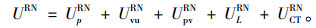
|
(9) |
整个供应链网络存在一些基础约束条件。层之间要达到网络均衡,约束条件式(10)~(13)为系统满足物流平衡条件;式(14)和(15)表示政府为了鼓励竞争、防止垄断的强制约束条件;式(16)~(18)表示分销网络节点库存容量设计限制; 式(19)到(21)表示分销网络节点承载的物流量。
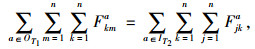
|
(10) |
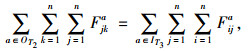
|
(11) |
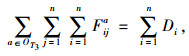
|
(12) |
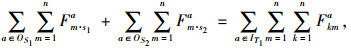
|
(13) |
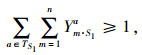
|
(14) |
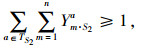
|
(15) |
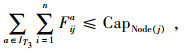
|
(16) |
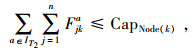
|
(17) |
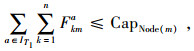
|
(18) |
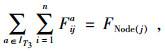
|
(19) |
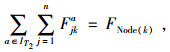
|
(20) |
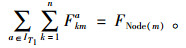
|
(21) |
整个弹性网络的约束条件,除了基础约束条件,还有以下一些:
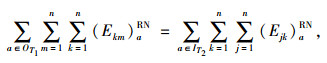
|
(22) |
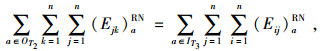
|
(23) |
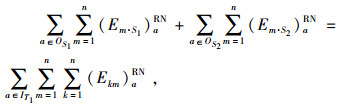
|
(24) |
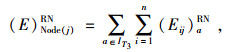
|
(25) |
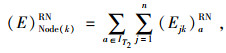
|
(26) |
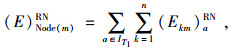
|
(27) |
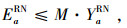
|
(28) |
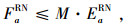
|
(29) |
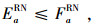
|
(30) |
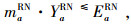
|
(31) |
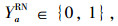
|
(32) |
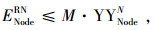
|
(33) |
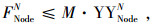
|
(34) |
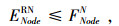
|
(35) |
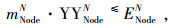
|
(36) |
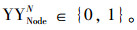
|
(37) |
式(22)~(24)表示期望物流平衡条件;式(25)~(27)表示节点的期望物流总量;式(28)表示只有被选弧上才存在期望流。式(29)表示只有在期望流为正值时,常规流才可能存在。式(30)表示物流量的期望值不可能大于常规物流量。式(31)表示最小期望物流量约束。式(34)~(37)的定义依次和式(28)~(31)类似。
3 案例分析以沿海地区某品牌汽车分销供应网络为例,网络包括末端需求市场di(i=1,2)、中间共三级的分销商(j, k, m=1.2···n,这里n=8)、前端竞争型的两个制造商(S1和S2)。产品分销区域包括西部地区、中部地区和沿海地区。包括两个制造商提供产品,都在中部地区;中间三级分销商各有2个在西部地区、3个在中部和沿海;需求市场都在中部。综上所述,整个供应网络包含28个节点和160条弧,通过Lingo软件结合分枝定界算法求解,模型数值均经过上万次的迭代。一些参数取值范围的说明如下。
◆ρ∈[0, 1]-多源供应的程度;
◆loss∈[α, +∞] -成本损失的程度;
◆apv1, apv2 and apv3∈[0, 1]-分销层layer的可靠性的程度;
◆Uv1, Uv2, Uv3∈[0, +∞]-库存有冗余容量的惩罚程度;
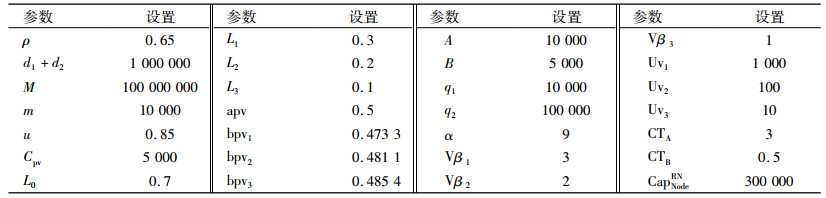
基础数据设置如表 1所示。
| 表 1 模型参数设置 Tab. 1 Model parameters settings |
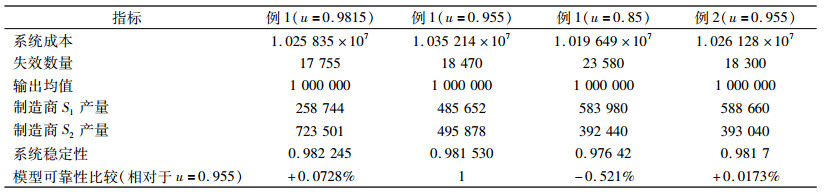
在此考虑2种实例,例1和例2为不考虑企业信任度约束下的弹性网络设计,例1考察的是单级期望容忍水平变化的供应链弹性网络设计,例2则考察的是处于全球供应链中的国内和国外竞争型制造商的弹性网络设计。
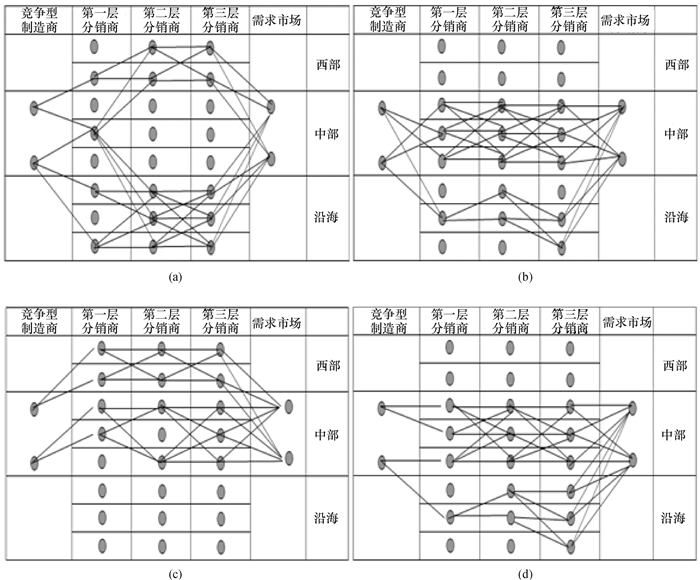
例1 考察3种不同的期望容忍水平u, 分别进行求解和仿真,考察u的变化对模型(9)的影响,分别得到了3种不同的多源动态弹性架构,如图 3(a)、(b)和(c)所示。
|
图 3 例1与例2的弹性网络架构 Fig. 3 Resilient network structures of cases 1 and 2 |
图 3(a)、(b)和(c)分别对应的期望容忍水平u为0.981 5、0.955和0.85,从而得到弹性供应网络架构。从图 3可以看出,每一级都选了2个以上的分销商,实现了多源供应。系统随着期望容忍水平的不断降低,主要采购从最初的沿海,转变到中部,最后到了西部地区。3种架构的绩效评估如表 2。
| 表 2 系统绩效评价 Tab. 2 System performance evaluation |
从表 2可以看出,系统随着期望容忍水平u的不断降低,成本先增长然后下降,这说明系统可靠性到了一定程度以后,降低系统稳定性会增加系统成本,但是成本优势使得很多制造商都铤而走险,选择风险大但是价格低廉的运输路线,使得系统成本不增反跌。系统失效数量同期望容忍水平成反比,输出均值保持不变。处于竞争的两个制造商S1和S2,在低水平容忍状态下时,S1的市场份额略多于S2。但是随着期望容忍水平的不断提高,S1在竞争中慢慢处于劣势。可以看出,系统可靠性与期望容忍水平成正比。
例2 考虑全球供应链的弹性架构,假设处于竞争中的2个供应商S1和S2,一个在国内(S1),而另一个从国内搬迁到了海外(S2)。S1的CTA为3元/单位,S2的CTA成本为300元/单位。以期望容忍水平u=0.955为例,进行求解,得到弹性架构如图 3(d)。由图可以看出,系统分销路线没有太大变化,该架构的绩效评估见表 2。
由表 2可以看出,均衡中的竞争局面被打破了,处于全球供应链中的国内制造商S1的生产量增加,国外制造商S2的生产量减少,从而失去了竞争优势。系统的失效数量减少了,可靠性得到了提高,比以前有了更强的稳定性。处于全球供应链中的系统成本减少了,原因是系统选择了更低价的制造商。
4 结论相对于强调干扰后调整的应急管理和干扰过程中局部调整的干扰管理,如何设计动态的供应链架构应对未知的风险,迅速恢复生产运作,维持预期收益,在越来越强调供应链成员关系的今天,显得尤为重要。本文给出了供应链弹性管理的概念,设计了一种弹性供应网络,并将其图形化地给出了集弹性制造定价/弹性空库存惩罚/弹性预警/弹性成员选择/弹性拥堵延迟/弹性运输于一体的供应架构。当系统遇到中断或者失效后,能够迅速对逆向各级成员进行筛选和认证,重新设计系统架构。利用以系统成本最小化为目标建立的网络设计,引入多级期望容忍服务水平,考虑每个回收层之间物流平衡问题,得到了最终优化的多级多源弹性逆向网络,从而建立了一套有效的弹性网络设计与优化方法。
研究表明,随着期望容忍水平的变化,系统成本因为分销商可靠性的降低呈凸规则变化,失效数量不断提高。此外,本章还有一些地方值得以后思考。如果系统是多种类产品分销,产品之间存在互补,不同级别分销商之间存在不同提前期,提前期会随着竞争型供应商的市场优势变化而扰动,如何根据分销商库存容量的变化进行再设计,这都是未来值得深入研究的方向。
| [1] |
FANG H, XIAO R. Cycle quality chain early warning network with e-channel lead time disruption[J].
International Journal of Systems Science: Operations & Logistics, 2014(ahead-of-print): 1-21.
|
| [2] |
TANG C S. Perspectives in supply chain risk management[J].
International Journal of Production Economics, 2006, 103(2): 451-488.
DOI: 10.1016/j.ijpe.2005.12.006. |
| [3] |
CHRISTOPHER M, LEE H. Mitigating supply chain risk through improved confidence[J].
International Journal of Physical Distribution & Logistics Management, 2004, 34(5): 388-396.
|
| [4] |
GONG J, MITCHELL J E, KRISHNAMURTHY A, et al. An interdependent layered network model for a resilient supply chain[J].
Omega, 2014, 46: 104-116.
DOI: 10.1016/j.omega.2013.08.002. |
| [5] |
方晗炜, 肖人彬, 蔡政英. 双源渠道闭环供应链生产计划的一种干扰恢复模型[J].
控制与决策, 2011, 26(9): 1303-1309.
FANG Hanwei, XIAO Renbin, CAI Zhengyin. Disruption restoration model in production planning with the closed-loop supply chain between dual-channel[J]. Control and Decision, 2011, 26(9): 1303-1309. |
| [6] |
CARVALHO H, BARROSO A P, MACHADO V H, et al. Supply chain redesign for resilience using simulation[J].
Computers & Industrial Engineering, 2012, 62(1): 329-341.
|
| [7] |
PONOMAROV S Y, HOLCOMB M C. Understanding the concept of supply chain resilience[J].
The International Journal of Logistics Management, 2009, 20(1): 124-143.
DOI: 10.1108/09574090910954873. |
| [8] |
王新平, 赵林度. 基于价格调整策略的多产品供应链弹性研究[J].
系统工程学报, 2013, 28(5): 641-650.
WANG Xinping, ZHAO Lingdu. Resilience management for a multiple-product supply chain based on price adjusting strategy[J]. Journal of Systems Engineering, 2013, 28(5): 641-650. |
| [9] |
SINGH A R, MISHRA P K, JAIN R, et al. Design of global supply chain network with operational risks[J].
The International Journal of Advanced Manufacturing Technology, 2012, 60(1): 273-290.
|
| [10] |
MANUJ I, MENTZER J T. Global supply chain risk management strategies[J].
International Journal of Physical Distribution & Logistics Management, 2008, 38(3): 192-223.
|
| [11] |
J?TTNER U, PECK H, CHRISTOPHER M. Supply chain risk management: outlining an agenda for future research[J].
International Journal of Logistics: Research and Applications, 2003, 6(4): 197-210.
DOI: 10.1080/13675560310001627016. |
| [12] |
KLIBI W, MARTEL A. Modeling approaches for the design of resilient supply networks under disruptions[J].
International Journal of Production Economics, 2012, 135(2): 882-898.
DOI: 10.1016/j.ijpe.2011.10.028. |
| [13] |
MITRA K, GUDI R D, PATWARDHAN S C, et al. Towards resilient supply chains: Uncertainty analysis using fuzzy mathematical programming[J].
Chemical Engineering Research and Design, 2009, 87(7): 967-981.
DOI: 10.1016/j.cherd.2008.12.025. |
| [14] |
SAWIK T. Selection of resilient supply portfolio under disruption risks[J].
Omega, 2013, 41(2): 259-269.
DOI: 10.1016/j.omega.2012.05.003. |
| [15] |
KRISTIANTO Y, GUNASEKARAN A, HELO P, et al. A model of resilient supply chain network design: A two-stage programming with fuzzy shortest path[J].
Expert Systems with Applications, 2014, 41(1): 39-49.
DOI: 10.1016/j.eswa.2013.07.009. |
 2016, Vol. 19
2016, Vol. 19