2. 上海交通大学 安泰经济与管理学院,上海 200030
2. Antai college of Economics & Management, Shanghai Jiao Tong University, Shanghai 200030, China
销售努力最早是从营销学中被提出来的概念,表示为促进市场销量而进行的一系列活动。衡量销售努力的变量称为销售努力水平[1-2]。销售努力包括增加销售人员、加大广告投入、将产品摆放在合适的货架上等,这些活动对于突出产品优势、拉动产品需求至关重要。在将销售努力水平引入供应链后,多数文献都是研究加入了销售努力水平因素之后的供应链是否协调以及通过设计怎样的契约可以达到供应链的协调,很少考虑供应链上的企业具有资金约束的情形。然而现实生活中,供应链上的许多参与主体都是中小企业,由于缺乏可用于抵押的不动产,常常面临融资难问题。存货质押供应链融资模式的产生为中小企业解决融资问题开辟了新的思路,银行和第三方物流企业也可通过开展存货质押融资来开拓业务,获取新的利润增长。
从定性的概念研究中到定量的质押率决策研究,存货质押融资的相关文献系统而全面。张钦红[3]假设质押物市场需求不确定且融资企业存在违约时,研究了银行在风险中性、风险规避和损失规避等情形下如何决策质押率的问题,并对3种偏好下的决策结果进行了对比分析。李毅学和冯耕中[4]假设质押物市场价格随机波动,并举例研究了价格服从几个具体分布时,下侧风险规避的银行如何决策最优质押率。李毅学和汪寿阳等[5]从物流企业的角度研究存货质押率问题。基于统一授信融资模式,物流企业获得银行一定的授信额度,对质押存货进行价值评估、监管仓储和进行贷款决策,构建了融资约束下的报童模型,借鉴主体+债项的风险评估思路,分析了物流企业在下侧风险规避时如何决策最优存货质押率。这些文献对于本文开展存货质押研究具有非常好的借鉴作用。
本文考虑一个简单二级供应链,供应商向零售商出售单一产品,零售商不做任何深加工,直接销售至终端市场,产品的需求随机且受到零售商销售努力水平的影响。零售商为缺乏资金的中小企业,需要向商业银行申请存货质押贷款。在签订贷款协议之前,零售商需要同时决策存货质押量和销售努力水平。本文首先分析了零售商的决策,给出了最优存货质押量和销售努力水平的表达式,接着分别分析了风险中性和损失规避[6-7]下的银行最优质押率决策。需要指出的是,本文为计算推导方便,与Taylor一样采用积的形式,假设市场需求D=eξ,e为销售努力水平,ξ为市场需求的随机变量,且假设ξ在[0, M]上服从均匀分布,其概率密度函数为f(ξ)=1/M,累积分布函数F(ξ)=ξ/M,2个分布函数满足广义失效率递增性质。市场需求随着销售努力水平提高而增大,但由于潜在顾客的有限性以及市场的逐渐饱和,使得努力活动的影响到后期是边际递减的,所以市场需求增加的速度是递减的,即D′(e)>0,D″(e) < 0。当然销售努力的付出必然会招致成本的发生,且该成本应当与销售努力水平密切相关,随着销售努力水平的增加而增大,销售成本函数符合性质g(0)=0, g′(e)>0, g″(e)>0,这反映了零售商在努力水平为0时,付出的努力成本也为0,并且随着销售努力水平增大,成本随之提高,这是符合现实情况的。参考了Taylor[1]在2002年一篇文章的叙述,本文假设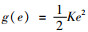
零售商自由资金为B,在销售季节到来之前,预计市场上会有产品A的需求,且该需求会随着销售努力水平的提高而增加,因此零售商先利用自有资金向上游供应商以w的批发价格订购产品,并以其中部分产品qm作为存货质押到银行指定的第三方物流仓库,待物流企业对该存货进行价值评估合格后,银行与零售商签订存货质押融资协议,以产品市场价格p、贷款利率rb向零售商提供贷款λpqm(λ为存货质押率),并同时成立一个封闭账户,零售商获得贷款后再向供应商进行二次订货,并决策相应的销售努力水平e。在销售季节做出销售努力向市场销售产品,在销售季节末,将质押物的销售收入和未售出产品的残值收入存入银行事先指定的封闭账户,作为偿还银行本息的资金来源。银行的存款利率为r0。
为方便后续的推导,提出如下假设:
1) 质押存货价格保持稳定,但需求面临市场随机波动,且受销售努力水平的影响;
2) 供应链双方均不考虑缺货成本;
3) 供应商和零售商之间为批对批策略,供应商按订单生产,不考虑库存、物流和缺货费用,供应商生产能力不受限制;
4) 供应商和零售商都是完全理性的,在开展存货质押融资业务中都是基于自身利润最大化原则来进行最优决策;
5) 只考虑单个周期,并且零售商只有在销售季节初期有一次订货机会,不考虑订货成本和订货周期。
2 零售商的存货质押融资决策模型零售商初始资金为B,且初始资金不足,上游供应商也急需资金不愿意提供延期支付的交易信用合同,因此融资企业只能通过向银行申请存货质押来获取银行贷款。开展存货质押融资的过程如下:零售商先用初始资金B向上游供应商订货,并将一部分产品qm(qm≤B/w)作为质押物向银行提出贷款申请,待第三方物流企业价值评估鉴定完毕符合贷款资格以后,零售商得到银行的贷款额λpqm,再向上游供应商进行第2次订购,因此整个销售季零售商总的订货量为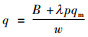
命题1 考虑市场需求受到零售商销售努力水平影响,在采用存货质押融资方式下,零售商的最优初始存货质押量为qm*,且具有以下性质:1)零售商的销售努力水平越高,存货质押量越大;2)银行所制定的存货质押率越大,存货质押量越小;3)质押贷款利息率越高,存货质押量越小。
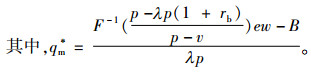
|
(1) |
证明1:零售商销售期末的利润函数可表示为
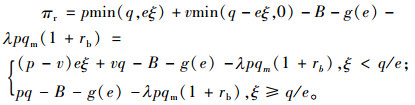
|
(2) |
因为零售商存在二次订购,因此总的产品订购量为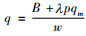
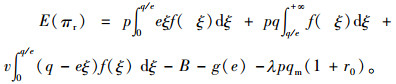
|
(3) |
首先决策零售商的初始质押量qm,对利润函数求订货量的一阶、二阶偏导数可得
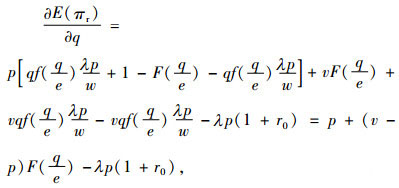
|
(4) |
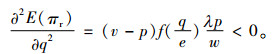
|
(5) |
可见零售商的期望利润函数是关于总订货量的严格凹函数,从而存在一个最优的订货量q*使得零售商期望利润最大化,其满足。
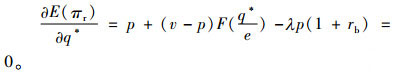
|
(6) |
计算可得零售商的最优总订货量
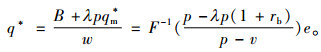
|
(7) |
因此可求出零售商的最优初始质押量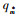
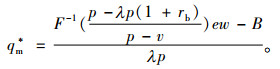
|
(8) |
最优存货质押量确定之后,按照同样的推导方法,零售商还要决定在销售季应该采取的最优销售努力水平。
命题2 零售商在向银行申请存货质押融资时,所应采取的最优销售努力水平为e*,且具有如下性质:1)随着零售商订货量q的增加而提高;2)随着销售努力成本系数K的增大而降低。
证明2:对零售商利润函数求期望可得
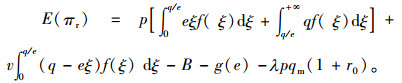
|
(9) |
对利润函数求关于销售努力水平的一阶、二阶偏导数,分别可得
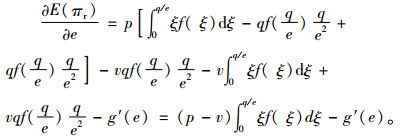
|
(10) |
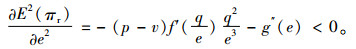
|
(11) |
从式(11)可以看出零售商的期望利润函数是关于销售努力水平的严格凹函数,因此存在一个最优的销售努力水平,使得零售商的期望利润最大。为了得出最优销售努力水平的显示解,利用假设f(ξ)=1/M,令一阶偏导数等于0。
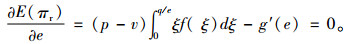
|
(12) |
可求得最优的销售努力水平e*,
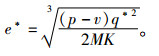
|
(13) |
银行作为出资方,需要决定最优的质押率,即银行提供的质押贷款额与质押物价值的比率。作为银行的一个核心决策变量,存货质押率受到多种因素影响,包括质押物特性、存货质押贷款利率、融资企业的信誉等。如果存货质押率定得太高,银行面临的违约风险会增大,会打击其提供贷款的积极性;定得太低,对融资企业缺乏吸引力。因此决策一个合适的存货质押率对于吸引交易各方参与存货质押业务非常重要。
3.1 风险中性下银行的存货质押融资决策模型风险中性下的银行在开展存货质押贷款业务时,既不冒险,也不保守,其效用函数即为期望利润函数。
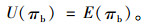
|
(14) |
首先来考虑零售商违约的情况。在销售期末,若质押物的销售收入和残值收入不能抵偿银行的贷款本息,此时零售商有可能选择违约,假设违约概率为α,为外生变量,银行只能获得质押物的销售收入和残值收入peξ+v(qm-eξ);当然零售商也可能以1-α的概率选择补全差额,偿清本息和,此时银行收益为λpqm(rb-r0)。
命题3 零售商的破产概率为
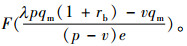
|
(15) |
证明3:首先求出零售商违约的市场需求临界值,若质押物的销售收入和残值收入不能抵偿银行的贷款本息λpqm(1+rb),此时零售商面临破产风险,银行可启动破产清算程序。
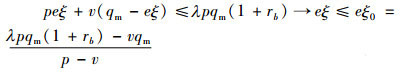
|
(16) |
因此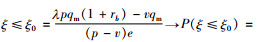
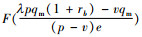
命题4 当市场需求受到零售商销售努力水平影响时,风险中性下的银行最优存货质押率为min(λ*, 1),且该质押率具有如下性质:1)零售商销售努力水平e越高,质押率λ*越高;2)初始质押量qm越大,质押率λ*越低;3)零售商违约概率α越高,质押率λ*越低。其中
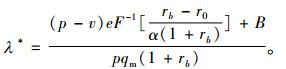
|
(17) |
证明4:考虑零售商违约概率为α情况下,银行的利润函数可以表示为
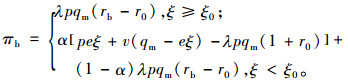
|
(18) |
对上述利润函数求期望可得
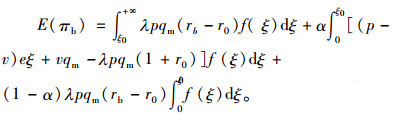
|
(19) |
对银行的期望利润函数关于质押率分别求一阶和二阶偏导数可得
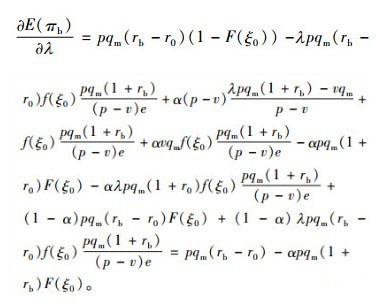
|
(20) |
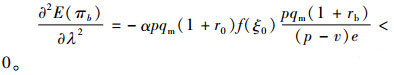
|
(21) |
可见银行利润函数是关于存货质押率的严格凹函数,因此存在一个最优存货质押率使得银行的利润达到最大。
令 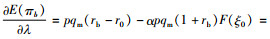
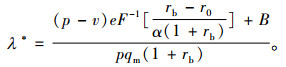
|
(22) |
由于λ*的取值范围是[0, 1],则风险中性下银行最优的存货质押率为min[λ*, 1]。
上面的推导过程可以看出,当零售商面临的市场需求与销售努力水平有关时,风险中性下的银行将采取的最优存货质押率为λ*,并且存货质押率随着销售努力水平提高而增大。这是因为在零售商销售努力水平越高时,银行对未来预期更加乐观,认为零售商能够卖出比原来更多的产品,这样零售商遵守贷款协议,到期能够足额偿还所欠的本金和利息的可能性更大,银行面临毁约的风险越小,因此银行愿意提高存货质押率,更多地贷款给零售商。
其他2个性质也很直观,符合现实情况。零售商违约概率越大,银行面临的潜在风险也越高,因此愿意提供的贷款额越小,质押率越低;此外,期初的存货质押量越大,银行有理由认为在销售季节末,产品由于各种原因滞销的可能性也越大,零售商到期无法偿还贷款本息和的概率也越大,因此为了降低风险银行愿意提供的质押率也越小。
3.2 损失规避下银行的存货质押融资决策模型现实生活中的银行都会考虑风险问题,并且把风险因素加入到自己的决策模型中。前景理论表明经济行为主体往往对收益的增加是风险规避的,而对收益的损失是风险偏好的,经济学将这种行为定义为“损失规避(loss-aversion)”。损失规避的含义是,相对于收益,决策方会更加看重损失,即一定量的收益带来的正效用要小于同等数额的损失给决策方造成的负效用,这就是普遍存在的损失规避现象。针对银行的损失规避性,本文采用了目前广泛用于行为经济学、管理科学等领域的简单分段线性函数来描述,它是对Kahneman和Tversky[38]提出的非线性损失规避效用函数的一种近似表达。假设w代表决策方的财富,w0为决策方的初始财富,则决策方的效用函数为
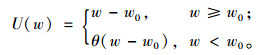
|
(23) |
其中,θ(θ≥1)代表决策方的损失规避系数,θ越大代表决策方的损失规避程度越高(θ=1代表决策者为风险中性),一般地,假设决策者的初始财富w0=0。这种分段线性形式的损失规避效用函数在行为经济学、管理科学等领域已得到广泛认可,其不仅能反映曲线基本特性,还可以简化计算过程。
命题5 当银行为损失规避型决策者,且市场需求受到零售商销售努力水平影响时,其最优的存货质押率为min(λ*, 1),且具有如下性质:1)零售商销售努力水平e越高,质押率λ*越高;2)零售商违约概率α越高,质押率λ*越低;3)损失规避系数θ越大,质押率λ*越低;4)初始质押量qm越大,质押率λ*越低。
其中, λ*满足下列一阶等式:
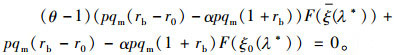
|
(24) |
其中,ξ= 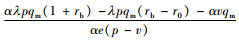
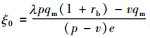
证明5:考虑银行的损失规避特性后,其利润函数为
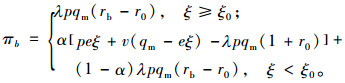
|
(25) |
令α[peξ+v(qm-eξ)-λpqm(1+r0)]+(1-α)λpqm(rb-r0)=0,可求得银行遭受损失的市场需求临界值ξ为
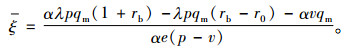
|
(26) |
求解银行的期望效用函数为
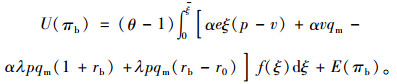
|
(27) |
从上式可以看出,银行的期望效用由两部分组成,一部分是期望利润E(πb),另一部分是修正因子θ-1和期望损失E(Lb)
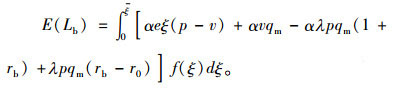
|
(28) |
对银行期望效用函数求关于存货质押率λ的一阶和二阶偏导数,分别可得
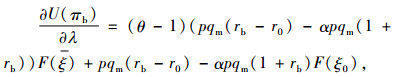
|
(29) |
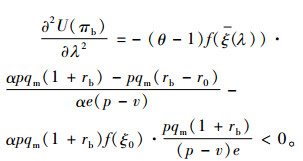
|
(30) |
可见银行期望效用函数是关于存货质押率的严格凹函数,因此存在一个最优的存货质押率λ*满足下列等式时,使得损失规避下的银行的期望效用函数达到最大。
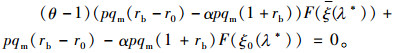
|
再来看存货质押率与其他几个参数变量的关系。
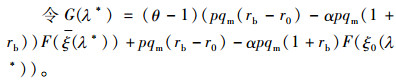
|
根据隐函数定理,可得
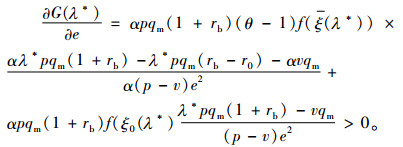
|
(31) |
即最优存货质押率随着销售努力水平的提高而增大,两者呈正相关关系。其他几个性质的证明过程类似,此处不再赘述。
该命题表明损失规避下的银行其最优存货质押率也是随着销售努力水平的提高而提高,不管其是否对风险规避,销售努力水平的提升始终是未来市场需求稳健的良好信号,所以银行会提升存货质押率,多贷款给零售商,从而获取更大效用。
4 数值模拟与算例分析本节通过数值模拟和算例仿真,来研究销售努力水平对零售商的存货质押融资决策,以及两种风险偏好下(风险中性和损失规避)银行的最优质押率决策等的影响。在验证上述结论的同时,用图形进一步模拟了零售商销售努力水平和最优初始质押量以及银行最优质押率的内在关系,希望对实践中想要采用存货质押融资策略的供应链相关主体提供一些建议和指导。
假设市场需求随机变量ξ符合[0, 50]上的均匀分布,即得出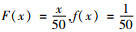
| 表 1 参数赋值 Tab. 1 The parameters value assignment |
算例1 销售努力水平对存货质押量的影响。
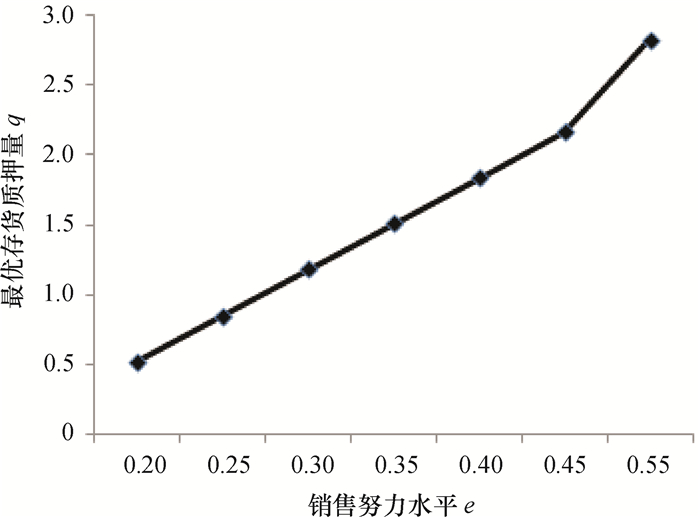
根据前文的结论,存货质押量受到多种因素,包括销售努力水平、贷款利率、批发价格、存货质押率以及初始资金等的影响。为了研究销售努力水平对存货质押量的影响,保持其他参数恒定不变,令λ=0.5。当销售努力水平变化时,最优初始存货质押量的变动情况如图 1所示。
|
图 1 不同销售努力水平下的最优存货质押量 Fig. 1 The optimal pledge volume corresponding to different sales effort level |
图 1的趋势表示,零售商采取的销售努力水平越高,其初始存货质押量越大。因为投入的销售努力越大,对市场需求前景期望越乐观,因此零售商会加大质押量以获取更多的银行贷款,从而向供应商进行更多的二次订货,来满足未来庞大的市场需求,提高收益和产品市场占有率。
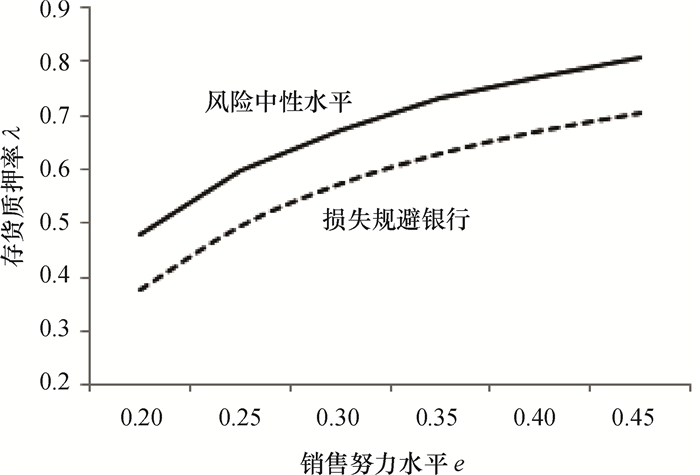
算例2 不同销售努力水平对风险中性和损失规避下的银行最优存货质押率影响。
对银行来说,销售努力的高低直接预示着未来市场销量的大小。当融资企业零售商提出贷款申请时,银行会对未来市场进行一个预估,从而决策一个最优的存货质押率。固定其他参数不变,并令违约概率α=0.1,对销售努力水平进行不同的赋值可得相应的风险中性或损失规避银行的最优质押率,如图 2所示。
|
图 2 不同销售努力水平下的银行质押率 Fig. 2 The optimal pledge rate corresponding to different sales effort level |
图 2表示,不管是风险中性还是损失规避的银行,其最优的存货质押率都会随着销售努力水平提高而增大。因为销售努力水平的提高,银行对未来市场需求前景更加乐观,因此零售商到期能够足额偿还贷款本息和的可能性越大,因此银行愿意多贷款给零售商,从而获取更多的利润。
5 结束语本文研究了销售努力水平影响需求情况下,中小企业零售商与银行、第三方物流开展存货质押融资业务时,销售努力水平对零售商和银行的融资运营决策影响研究。本文给出了零售商最优存货质押量和最优销售努力水平表达式以及风险中性和损失规避下银行的最优质押率表达式。证明了零售商的销售努力水平对各方的融资存在正面的影响,销售努力水平越高,零售商和银行对市场前景越乐观,因此零售商会提高存货质押量,银行会提高质押率来加大对零售商的贷款力度。最后通过数值模拟与算例分析,画图验证了结论中销售努力水平、初始存货质押量和存货质押率之间的关系。
由于篇幅有限,本文没能将有关问题考虑周全,需要在未来的研究中不断完善。首先,本文只考虑了银行具有损失规避的情形,而没有考虑零售商也具有损失规避的特性,但任何一个决策主体都有可能是损失规避的,未来的研究中可以加以考虑。此外,本文对银行损失规避特性的刻画是通过分段线性函数来体现的,然而前景理论中损失规避函数还有很多非线性表达形式。在未来的研究中可以引入其他损失规避函数形式进行分析。
| [1] |
TERRY A. Taylor. Supply chain coordination under channel rebates with sales effort effects[J].
Management Science, 2002, 48(8): 992-1007.
DOI: 10.1287/mnsc.48.8.992.168. |
| [2] |
KRISHNAN H, KAPUSCINSKI R, BUTZ D A. Coordinating contracts for decentralized supply chains with retailer promotional effort[J].
Management science, 2004, 50(1): 48-63.
|
| [3] |
张钦红, 赵泉午. 需求随机时的存货质押贷款质押率决策研究[J].
中国管理科学, 2010, 18(5): 21-27.
ZHANG Qinhong, ZHAO Quanwu. Research on loan-to-value ratio of inventory financing when demand is stochastic[J]. Chinese Journal of Management Science, 2010, 18(5): 21-27. |
| [4] |
李毅学, 冯耕中, 徐渝. 价格随机波动下存货质押融资业务质押率研究[J].
系统工程理论与实践, 2007, 21(12): 42-48.
LI Yixue, FENG Gengzhong, XU Yu. Research on loan-to-value ratio of inventory financing.under randomly-fluctuant price[J]. Systems Engineering-Theory & Practice, 2007, 21(12): 42-48. DOI: 10.3321/j.issn:1000-6788.2007.12.007. |
| [5] |
李毅学, 汪寿阳, 冯耕中. 物流金融中季节性存货质押融资质押率决策[J].
管理科学学报, 2011, 14(11): 19-29.
LI Yixue, WANG Shouyang, FENG Gengzhong. Decision ofloan-to-value ratios of seasonal inventory/pledge fnancing based on logistics finance[J]. Journal of Management Sciences in China, 2011, 14(11): 19-29. |
| [6] |
KAHNEMAN D, TVERSKY A. Prospect theory: An analysis of decision under risk[J].
Econometrica: Journal of the Econometric Society, 1979, 47(2): 263-193.
DOI: 10.2307/1914185. |
| [7] |
TIAN Yu, HUANG Dao. A loss-averse supply chain coordination modelling[J].
Control engineering of China, 2006, 13(4): 366-369.
|
| [8] |
曲道钢, 郭亚军. 需求与销售努力相关下混合渠道供应链协调研究[J].
运筹与管理, 2010(4): 8-13.
QU Daogang, GUO Yajun. On coordination of hybrid channel supply chain with effort dependent demand[J]. Operations Research and Management Science, 2010(4): 8-13. |
| [9] |
李绩才, 周永务, 肖旦. 考虑损失厌恶一对多型供应链的收益共享契约[J].
管理科学学报, 2013, 16(2): 73-76.
LI Jicai, ZHOU Yongwu, XIAO dan. Revenue-sharing contract in supply chains with single supplier and multiple loss-averse retailers[J]. Journal of Management Sciences in China, 2013, 16(2): 73-76. |
| [10] |
林志炳, 蔡晨, 许保光. 损失厌恶下的供应链收益共享契约研究[J].
管理科学学报, 2010, 13(8): 34-38.
LIN Zhibing, CAI Chen, XU Baoguang. Revenue sharing analysis of supply chain with loss aversion[J]. Journal of Management Sciences in China, 2010, 13(8): 34-38. |
| [11] |
WANG Y, GERCHAK Y. Supply chain coordination when demand is self-space dependent[J].
Manufacturing&Service Operations Management, 2001, 3(1): 82-87.
|
| [12] |
徐最, 朱道立, 朱文贵. 销售努力水平影响需求情况下的供应链回购契约[J].
系统工程理论与实践, 2008, 28(4): 1-11.
XU Zui, ZHU Daoli, ZHU Wengui. Supply chain coordination under buy-back contract with sales effort effects[J]. Systems Engineering-Theory & Practice, 2008, 28(4): 1-11. |
| [13] |
徐最, 胡一竑, 朱文贵. 贸易信用契约下零售商的运营决策分析[J].
上海管理科学, 2012, 34(5): 28-30.
XU Zui, HU Yihong, ZHU Wengui. The retailer's operational decision analysis under a trade credit contract[J]. Shanghai Management Science, 2012, 34(5): 28-30. |
| [14] |
叶阿真, 刘晓敏, 韩凤萍. 销售努力影响需求下的供应链协调契约研究[J].
莆田学院学报, 2010, 17(4): 37-43.
YE Azhen, LIU Xiaomin, HAN Fengping. On Supply Chain Coordination Contract with Sales Effort Effects[J]. Journal of Putian University, 2010, 17(4): 37-43. |
 2016, Vol. 19
2016, Vol. 19
