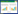文章信息
- 徐喜平
- XU Xi-ping
- 长泽龟之助的数学翻译交流活动评述
- A Commentary on Exchanges in Translation of Mathematical Works by Kamenosuke Nagasawa
- 广西民族大学学报(自然科学版), 2017, 23(2): 30-35
- Journal of Guangxi University for Nationalities(Natural Science Edition), 2017, 23(2): 30-35
-
文章历史
- 收稿日期: 2017-03-15
长泽龟之助(1860-1927) 是日本明治、大正时期的民间数学教育家,他在翻译引进西方数学知识和编撰数学教科书方面成绩突出,一生编译教科书达150多部.他翻译的教科书不仅在日本各中等学校广泛使用,还被翻译为中文,作为晚清、民国时期各中小学堂的教材使用,他编撰的数学词典在日本非常受欢迎,而且1937年由中国学者薛德炯和吴载耀翻译为中文在中国出版,直到20世纪80年代还是中国中小学教师备课的首选工具书.长泽在编译数学教材方面取得突出成绩是他长期不间断翻译西方著作结出的硕果.但一生150本数学教材的问世也绝非他一人之功,日本国内的数学家、学者、教员都做了大量工作,同时他和外国数学家的交流活动也成为他编译数学教材的重要推动力.目前,日本数学史、中日数学交流史、数学翻译史的研究中还未见这方面的系统研究,故笔者将主要探讨长泽与日本及其他国家数学家和学者的合作与交流,以期完整展示长泽的数学交流与国际交往,指出长泽和国内外数学家、学者、教员的合作在其数学教材编译工作中的重要性.
1 长泽龟之助与日本学者合作编译教科书长泽龟之助于明治八年(1875) 入长崎师范学校学习数学,该校校长佐原纯一(1841-1920) 是长崎海军传习所的一期生,原名佐原纯吉,庆应二年(1866) 从长崎来到东京,在开成所教授数学,翌年出任开成所二级教授. [1]在校期间,长泽对数学产生了浓厚兴趣,而佐原纯一极有可能就是长泽的数学启蒙老师.
明治十一年(1878) 长泽毕业之后,曾在京都开过私塾,之后去东京,加入了东京数学会社.东京数学会社在数学家神田孝平和柳楢悦倡导下,于明治十年(1877) 在日本东京成立,当时参加东京数学会社的成员既有川北朝邻、远藤利贞、福田理轩、大村一秀等和算家、也有中牟田仓之助、赤松则良、中川将行、荒川重平、菊池大麓等洋算家,还有上野清等民间数学教员.[2]会社成立之初就创办了该会社的社刊《东京数学会社杂志》,共发行67期,该杂志成为当时会社成员共同探讨数学知识的平台,对日本数学的普及、西方数学的传播以及数学教育与研究都起到了非常重要的作用.随着人们对西方数学知识的逐渐吸收消化,及其在军事、造船、机械中的应用展开,当时的数学家们逐渐由和算转向了研究洋算.东京数学会社的许多数学家如菊池大麓、神田孝平、冈本则录、川北朝邻、上野清还直接从事数学教育和编译教科书,为日本数学教育西洋化做出了重要贡献.在东京数学会社期间,长泽和会社成员中的许多知名数学家们交流,并开始在数学会社的杂志上投稿,研究解决数学问题的方法.从此长泽的数学能力开始逐渐显现出来.
上文提到的川北朝邻,1840年生于东京,六岁开始随神田泰雨学习汉字和算术,开始对数学发生兴趣.1857年师从村濑孝养学习点窜术,后又成为御粥安本和内田五观的弟子.1870年进入静冈学校开始学习洋算,并尝试用洋算知识来解决和算问题.此后在静冈县小学、静冈传习所、陆军兵学寮、户山学校、士官学校任教,编撰《笔算题丛》和《代数学教科书》,并和山本正至一起翻译《几何学原楚》,初步显示了他的译书能力.明治十年(1887) 协同神田孝平、柳楢悦等一起创立东京数学会社,承担《东京数学会社杂志》的编辑工作,并积极在杂志上投稿探索求解数学问题的方法.[3]在此期间,川北发现在日本缺少高等数学书,偶有一二,也囿于价格昂贵不能推广,所以从明治十四年(1881) 开始和上野清创立东京数理书院共同发起翻译出版高等数学书的工作.
该书院创立之初,川北在当年《东京数学会社杂志》上登载招聘广告如下:
“为进一步推进当今数理科学之发展,特招聘有志之士共同翻译出版西方数学书籍,有意者请与东京上野西黑门二十番地上野塾联系.现已着手翻译突氏《轴式圆锥曲线法》.
明治十四年(1881) 一月 川北朝邻上 野清”[3]
此时,长泽龟之助加入数理书院,和川北朝邻、上野清一起翻译西方数学著作,在短短三四年时间之内,数理书院共出版西方译著16部之多.其中长泽翻译的就有13部,可见其翻译能力.但1885年之后,未见数理书院出版长泽的译著.三上义夫在《川北朝邻小传》中指出:“之后出于其他原因,数理书院的翻译工作主要由市东佐四郎、向井嘉一郎两位承担.”[3]长泽从1882年开始便到川北创立的私塾立算堂上课.次年,长泽受聘于陆军部门,主要上数学课和编写教科书.[4]也许是由于教务繁忙而将数理书院的翻译工作委托给上述两人.
虽然如此,长泽也没有放弃他的翻译工作,而是更加积极主动地探求适合日本数学教学的西方教材.1887年,长泽和宫田耀之助合作翻译了英国数学家史密斯(Charls Smith, 1844-1916) 的《初等代数学》,之后他们一直合作编译教科书.长泽翻译约翰·可成(John Casey,1820-1891) 的《中等教科书平面三角法》(1888) 和Alexander Knox的《初学微分学》(1889) 时,宫田承担了校算工作,而且在1893年,长泽和宫田还共同撰译了Chapman的《方程式之理论》来补充史密斯代数学之不足.1892年宫田编撰出版《数学问题集算术、代数、几何》时,长泽曾为其校阅.
|
| 图 1 长泽和宫田共同撰译的部分书目 Fig. 1 Textbooks translated by Nagasawa kamenosuke and other Japanese scholars(1) |
除宫田之外,长泽的合作者还有西乡康三、藤木曾登吉、樱井幸作、东利作,他们主要负责一些翻译和译著的校算.
长泽译书阅历增加,经验丰富,他一边译书,一边帮助同行校阅数学书.1894年他曾帮宫崎繁太郎校阅其编撰的《史密斯初等代数学解式》,同年还为东京理学院院长真田兵义校阅其翻译的《几何教科书》.可见在经过数理书院及后来的翻译历练,长泽在翻译方面已经有所建树,具备独立把握译本中数学内容和校阅译著的能力,成为这方面的专家.
1896年,长泽编撰《中等教育算术书》订正八版时,在其序言中提到:
“……本书ノ问题、主トシて雑题ハ种种ノ原书ニ就キ之ヲ蒐集シ又自作ノモノノ外ニ宮田耀之助、今泉胜治二氏ノ撰ニ系ルモノモ少ナカラズ而シテ本书ノ校正ハ藤本曾登吉氏ハ印刷前ニ、川瀬弁道氏本文印刷后ニ全编ヲ熟読シ且、一一问题ヲ演算セラレ原稿ノ答ノ正否ヲ験スルノ便宜ヲ与へラレタリ余ハ深ク是等ノ诸君ノ労ヲ谢シ并セて刊行ノ上ハ江湖诸君ノ忠告ヲ希望ス.” [5]
由此序言可知,当时该书的练习题除收集原书习题和自编之外,宫田耀之助和今泉胜治也参与编写,而且该书在出版之前由藤本曾登吉进行校阅,出版之后川濑便道又通读全篇进行校对.另外在长泽1907年编《问题解法代数学词典》序言中也提到了和他合作编撰该书的人有:
堀内平次郎 佐久间仓吉 菊池亮三郎 西阪赖二郎 大橘留治
成濑四男也 福永荣治 宫崎镇美 江藤丰吉 庄野小八郎
增泽孙二 田洼房一 饭田一雄[6]
这些都说明当时长泽在编译书时,并不是一个人在努力,而是以他为中心已经形成一个学术团队,其中的堀内平次郎还在1904年和长泽合著了《解析几何学问题解》.

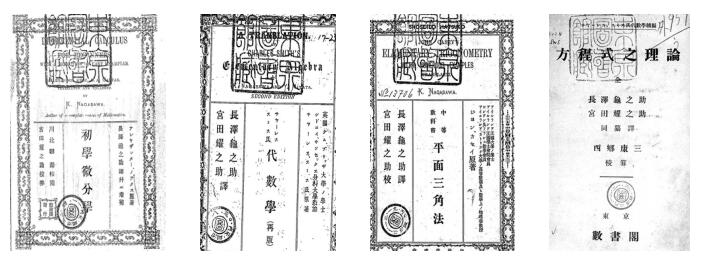
|
| 图 2 长泽和真田兵义等合作者完成的著作 Fig. 2 Textbooks translated by Nagasawa kamenosuke and other Japanese scholars(2) |
长泽之所以编译教科书数量如此之巨大,除了个人的努力之外,更得益于有这样一个强大的合作团队.另外他的教科书如此受欢迎,也得益于他的教学实践以及他经常和一线的数学教员进行交流.往往在教科书再版之际,就会听取他们的建议进行改进.例如1904年长泽编撰了《新几何学教科书平面》,在经过四年的使用之后于1907年进行了改版.在序言中长泽指出当时的中等教育几何学教科书注重理论,枯燥无味.而本书一改此弊端,通过四年的使用得到了各学校教员的一致认可,并根据各教员在使用过程中的意见进行改版.
1908年长泽编撰了《实业教育几何学教科书》,在1912年改版之际,长泽在序中也提到了“本书自刊行以来被多所实业学校使用,所以就该书的优劣我特意咨询了实业学校各教员,他们都给出了恳切的建议,所以在改版之际我按照他们的建议补充了书中正文的不足,同时在卷末增补了复习题.” [7]1925年出版的《新三角法教科书》序言中同样提到了“在编撰过程中,和全国现行教科书进行比较研究的同时还认真听取和讨论了教员的建议”[8]进行改订.
不仅这几本教科书得到了第一线教员的宝贵意见和指导,在其他教科书以及他一直主持的《XY》杂志中也可以看到长泽非常注重教科书的实践教学成果,并根据教员及学员的需要及时调整教学内容和教学方法.
所以,长泽从毕业以来就积极拓展数学交流,不仅和当时的著名数学家学习、辩论,还和一些学者共同翻译、编撰数学教材,在教材的使用过程中,他主动询问一线教员对于教材的改进建议,并及时改版.长泽数学能力的提高和众多教科书的编译完成是他个人积极努力的结果,同时也离不开众多数学家、学者、教员的帮助,长泽和本国数学家、学者的合作是他编译众多教科书的重要支撑.
2 长泽龟之助与中国学者探讨教科书编撰之法长泽除了和日本的数学家、学者、教员合作编译教科书之外,还和中国的数学家、学者有过交流,晚清的周达、崔朝庆、余恒等数学家都曾和长泽有过数学交流.周达在1902年受扬州知新算社委托去日本调查算学,限于时日,“所与深谈者,仅上野清、长泽龟之助二君.二君者,彼邦畴人中之泰斗.译书等身.彼邦算学界中,著述之富,舍二君外,殆无第三人矣.余与二君交,不足十日,而倾盖如故,若夙契然,终日谈算,娓娓不倦”.[9]33-34此次访学日本虽然和长泽属初次见面,但周达认为他与长泽如“电气之契合,盖仅见者,相见甫数日,然十年之谊,亦无以异矣.每当夕阳欲坠,松风怒号,午月当空,竹阴掩映,两人促膝对踞小楼上,赏奇析疑,雄谈浅酌,几不知身在异国”.[9]43
从此之后,长泽便和周达结下了深厚的友谊,互相通过书信往来探讨数学问题.长泽在1904年编译出版《几何学定理及问题》时,周达曾为其作序.而1906年周达翻译出版长泽的《新几何学教科书平面》时,长泽为该书作序表达了希望能为中国教育服务的愿望.除了周达之外,长泽还和江苏南通著名数学家崔朝庆交往甚密,他在1905年出版《解法适用数学辞书》时,崔朝庆曾为该书作序:
“日本算书,多于吾国数十倍,其中以长泽先生编译者为最多,近数年来输入吾国之书,足以汗牛充栋,故习算之士,无不知有长泽先生者.朝庆自庚子出都,就馆金陵,往往系邮便订购日籍,得算书百有余种,讲授之暇,尝搜辑各书中之表为算表合璧一编.其米突法度量衡表即撰择先生所著之算术教科书也.客冬有友人东渡,嘱持一帙以诒先生,因而就正,猥蒙许可,自此函犊往来,常获教益.”[10]
可见崔朝庆在教授数学课程时,就经常从日本邮购数学书籍作为参考,他在1902年编著的《算表合璧》是中国近代第一部学堂所用的综合科学用表.[11]其中的《米突法度量衡表》就是选自长泽的《算术教科书》.从此之后两人经常书信往来,获益匪浅.崔朝庆在1912年创办的《数学杂志》是中国近代最早的数学杂志之一,创办之初面临资金不足的问题,长泽曾慷慨解囊,为其赞助.[12]233-234
另外,长泽在1907年编撰《代数学精义》《三角法精义》和《几何学精义》时就分别由晚清成都通省师范学堂的林启一、两江师范学堂的余恒和包荣爵为其作序.这些中国数学家和学者在序中都高度评价了长泽在数学书翻译与编撰方面的成就,其中包荣爵在《几何学精义》的序中高度评价了长泽在几何学方面的贡献,将其誉为“今之欧几里得也”.而林启一在《代数学精义》序中指出:
“利玛窦东来,为我邦西算萌芽时代.咸同之间,李华诸氏又相继译述代微积诸书,以飨遗学子.厥后虽译著间出,率浅陋不足供钻研.不佞生平,颇嗜数理,知墨守十七世纪旧籍以自豪者,终类楚人之宝燕石.于是遂起游学泰东西之志.东瀛三岛与我邦仅一衣带水之距离.不佞乃先负笈其间,广购高深学之书目,攻究世界最新发明之学.而所购置,以长泽氏译著为最多.攻究之新理,又强半为氏译著中多包孕.不佞因是知现今东亚数学家之巨擘.”[13]
因为林启一认为“长泽氏译著为最多.攻究之新理,又强半为长泽氏译著中所包孕”,“乃出拙译斯氏解析几何学就正于长泽君,并咨访以教科书编撰法.君一见不佞,如旧好,竟日论述,无倦容,不佞受攻错益颇多,欲出所论述者,以编撰数学各科,贡我同志”.[13]
可见林启一留学日本的目的是学习西方最新之数学知识,为中国教学之用.而在当时日本翻译西方译著最多的就是长泽,所以他才赠书与长泽,向长泽咨询教科书编撰之法.长泽热情接待了林启一,两人整日讨论数学问题,林启一受益颇多,而且长泽还承诺为中国编撰数学各科教科书.其实后来,长泽编纂的很多教科书都被他的中国好友周达、余恒、张其详等翻译为中文出版,长泽还亲自为自己的汉译教科书作序.这些教科书在中国的出版发行对晚清民初的数学教育做出了重要贡献.[12]232-233
中国数学家周达、林启一都曾为寻求本国数学的发展之路专门赴日本学习数学,而且都和长泽有过亲密交谈.长泽还于1905年亲自来到中国和中国数学家进行交流.1905年长泽将新编撰完成的《新代数学教科书》书稿交由出版社之后,自己便踏上了“清国漫游之途”,当时该书的出版事宜全部交给了秀英社处理,而其中有关问题的校正、校算除了自己之外还委托给了田渊一郎和真边仙一.[14]那么长泽如此着急来中国到底所为何事,由于缺乏直接的史料支撑,笔者也不敢妄下结论,但是在1907年长泽出版《三角法精义》时,两江师范学堂的余恒曾为其作序,在该序中提到了此事.由该序可知余恒之前就读过长泽编撰的新数学教科书四种,其中有算数、代数、几何、三角.
然而“余以叹教科之书,至此观止矣,然参考之书,其完全者,尚不可多观.是故数学界之缺点,而余故不能不希望长泽君补救之者也.乙巳长泽君西游吾国,晤余于金陵,出所著卡氏几何学视余.展读一过,觉其搜罗宏富,解法完善,泃最良之参考书也”.[15]
由此可知,余恒认为长泽编撰的数学教科书已经非常完备,只缺数学参考书,希望长泽能够补其空缺,所以长泽才于1904年翻译出版了《卡塔兰氏几何学定理及问题》一书.而“乙巳长泽君西游吾国,晤余于金陵,出所著卡氏几何学视余”,乙巳年就是1905年,而长泽给余恒的卡氏几何学应该就是他刚刚出版的《卡塔兰氏几何学定理及问题》.当时东亚数学界缺乏参考书之现状不仅余恒注意到此事,长泽也深有同感,在《卡塔兰氏几何学定理及问题》的自序中,长泽就写道:“虽然近年我国有多种数学著作刊行,但是值得学者参考之几何学著作几乎没有,偶有一两本译书也都是偏重作图题或止于近世几何学,没有越出初等几何学之范畴,目前还没有系统介绍平面和立体几何的优良参考书供学者使用.”[16]
所以长泽此次西游清国的目的之一也许有将自己新出之参考书《卡塔兰氏几何学定理及问题》视于中国学者余恒,了却余恒“参考书是数学界之缺点,而余故不能不希望长泽君补救之者也”[15]的心愿,希望该书在中国推广,对中国数学教育有益.
除此之外,1906年长泽的《问题解法几何学词典》出版之际,薛光锜曾为该书作序如下:“凡学问至大备则复杂,而后辞书出.理法等科均有辞书矣,翳算独无,讵非遗憾欤.日本长泽君为当今算界泰斗,与吾为诤友.其所撰述,自算术至微积分学,既充斥东亚矣,兹以算之部分既广,未有辞书以导线,恐临岐与嗟者多也.……”[6]可见,薛光锜和长泽为挚友,他非常佩服长泽的数学才能而且对长泽的字典给予了很高的评价.
总之,长泽和晚清的数学巨匠周达、崔朝庆、薛光锜、包荣爵、林启一等都有过数学交流,他的许多日文数学书都由这些数学家作序,而这些中国数学家也是长泽数学教科书和字典在中国传播的有力推动者,其中周达、崔朝庆、包荣爵还将长泽的许多数学教科书翻译为中文在中国使用.他们彼此交流,相互借鉴彼此的数学成果,推动了东亚数学教育事业的发展.
3 长泽龟之助与欧洲数学家的翻译交流长泽与欧洲数学家的交流主要体现在数学翻译方面,因为他翻译了众多西方数学家的著作,所以在翻译过程中经常和这些数学家进行沟通,以期完整展现原书内容.有时候为将外国数学著作介绍到日本,为译一本适合日本数学教育的数学教科书,他还亲自和该国数学家联系,征得翻译许可.长泽在翻译英国数学家库利斯塔尔(George Chrystal,1851-1911) 的Introduction to algebra时,有关翻译事宜就曾和作者本人及其出版社做过多次沟通.
库利斯塔尔的Introduction to algebra在英国于1898年4月出版,长泽在1899年11月写信给著者及出版社,征得翻译许可.对方答应该书只有长泽一人有日文翻译权,不得转交他人.所以长泽在该书的第二页写上“翻译权所有”的字样.经过两年的努力,1901年长泽将该书翻译完成.在该书出版之际,原著者库利斯塔尔还亲自为该书作序,并将自己的照片寄来,长泽将照片附在该书的著者序文之后.其实在翻译过程中,长泽也遇到了很多翻译难题.为了更贴切地将原书内容呈现给读者,为了更好地反映著者的思想,他还经常就某些问题和著者书信讨论.[17]9
1901年长泽完成了该书的翻译工作,书名译为《新著代数学》.其实该书的编撰目的是“改良英国代数学教授法”,所以作者在编撰内容和形式方面和当时的其他著书有所不同.长泽之所以翻译该书也许就是因为它的与众不同.因为在该书出版之前日本的代数学大致“只有樱井、千本二氏合译的代数学以及长泽翻译的史密斯代数学二三书,日本数学学习者希望看到崭新的代数学书,是而长泽翻译了刚刚在英国出版的Introduction to algebra”.[17]8可见,长泽推陈出新的翻译态度.
长泽在数学教育及教科书的编撰与改良方面,不仅和许多中国数学家有过讨论,还积极求教于英国数学家.正是他的这种国际交流与合作的广阔视野成就了他翻译工作的巅峰.
4 小结长泽龟之助编译的数学教材在日本数学教育史上留下了光辉一页,他一生编译教科书达150多部,这些教科书的编撰方法、知识体系、形式创新得到了明治时期日本,以及晚清民国时期的中国数学教育的认可,影响深远.而这些教材的成功编译离不开他与本国及其外国数学家的交流,他在日本积极寻求合作者并取得成功,使他能够迅速将自己的翻译成果转化为教学实践.而他在日本教学实践的成功经验又通过和中国数学家的交流引入中国,指导了晚清、民国时期的中国数学教育.这一过程都得益于他将目光投向西方,时刻关注西方数学教育及新教科书的出版,他与西方数学家虽然没有直接面对面的交流,但通过数学教科书交流思想、传播知识,最终形成了长泽独特的数学教科书编撰法并推而广之.在长泽长达40多年的翻译生涯中,积极拓展国际交流,同时注意和本国学者及教员的合作.所以才能使自己的教学理念、教科书编撰法及其知识体系与时俱进,适应当时的教育实况.可以说长泽的翻译工作是他数学教育工作的基础,而广泛的翻译交流活动是长泽翻译水平和编撰能力不断提高的推动力,所以要全面评价长泽在数学教育方面的成绩就不得不重新审视他的数学编译交流活动.
| [1] | 安藤洋美. 明治数学史の基础工事[J]. 桃山学院大学人间科学, 2000, 19: 46. |
| [2] | 萨日娜. 清末中国と明治期の日本における西洋数学の受容——両国间の文化と教育における交流を中心に[D]. 东京: 东京大学大学院総合文化研究科, 2008: 95-98. |
| [3] | 三上义夫. 川北朝邻小伝[M]. 神奈川: 港栄社印刷所, 1941: 1-18. |
| [4] | 冯立升. 中日数学关系史[M]. 济南: 山东教育出版社, 2009: 282. |
| [5] | 长泽亀之助. 中等教育算术书[M]. 东京: 数书阁, 1896: 6. |
| [6] | 长泽亀之助. 问题解法代数学辞典[M]. 东京: 郁文社, 1907: 序. |
| [7] | 长泽亀之助. 新几何学教科书平面[M]. 东京: 宝文馆, 1912: 序. |
| [8] | 长泽亀之助. 新三角法教科书[M]. 东京: 成美堂, 1925: 序. |
| [9] | 周达. 日本调查算学记[M]. 上海: 中西书局, 1903: 33-34, 43. |
| [10] | 长泽亀之助. 解法适用数学辞书[M]. 东京: 郁文社, 1905: 序. |
| [11] | 陈克胜, 郭世荣. 中国第一部近代学堂所用的综合科学用表——《算表合璧》[J]. 中国科技史杂志, 2012, 33(1): 11–21. |
| [12] | 代钦. 数学教育与数学文化[M]. 呼和浩特: 内蒙古教育出版社, 2013: 232-234. |
| [13] | 长泽亀之助. 代数学精义[M]. 东京: 成美堂, 1907: 1. |
| [14] | 长泽亀之助. 新代数学教科书[M]. 东京: 日本书籍株式会社, 1905: 6. |
| [15] | 长泽亀之助. 三角法精义[M]. 东京: 成美堂, 1907: 1-2. |
| [16] | 卡塔兰氏. 几何学定理及问题[M]. 长泽亀之助, 译. 东京: 日本书籍株式会社, 1904: 3. |
| [17] | 库利斯塔尔. 新著代数学[M]. 长泽亀之助, 译. 东京: 成美堂, 大阪: 集成堂, 1901: 9. |
 2017, Vol. 23
2017, Vol. 23