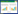文章信息
- 彭勇, 罗佳
- PENG Yong, LUO Jia
- 需求可拆分车辆路径优化模型与BLF-GA算法设计
- Researching on Optimization Model and BLF-GA Algorithm of Split Delivery Vehicle Routing Problem with two-dimensional loading Constraints
- 广西民族大学学报(自然科学版), 2017, 23(2): 67-73
- Journal of Guangxi University for Nationalities(Natural Science Edition), 2017, 23(2): 67-73
-
文章历史
- 收稿日期: 2016-11-30
2. 宜宾学院 经济与管理学院 四川 宜宾 644000
2. Economics & Management School, Yibin University, Yibin 644000, China
车辆路线安排问题最早由Danting和Ramser[1]在1959年提出,此后车辆路径问题得到了越来越多的关注,带时间窗、多种车型、多个配送中心等车辆路径问题被提出.彭勇等人[2-3]在研究车辆路径问题时,考虑车速会因为时间、路段不同而变化后,运用粒子群算法、Dijkstra-GA算法优化路径.1989年Dror & Trudeau首次提出了需求可拆分车辆路径问题(Split Delivery Vehicle Routing Problem, SDVRP)的概念,[4]并提出SDVRP是在标准车辆路径问题上对“每个客户点的需求只能由一辆车进行配送”这一约束条件的松弛,在标准车辆路径问题的基础上进行扩展,允许每个客户点的需求被两辆及以上的车辆进行配送,这一松弛约束可以减少配送车辆以及行驶总路径长度.至今为止,针对需求可拆分车辆路径问题已有大量的研究方法.研究学者们开始对SDVRP进行扩充,即在VRP问题中不仅考虑客户需求能由两辆及以上的车辆同时进行配送这一松弛约束,还考虑了其他约束条件,如Frizzell和Giffin[5-6]在SDVRP中还考虑了时间限制.Lee、Marina等人[7]在SDVRP中考虑车场不是单一的,即多车场的需求可拆分车辆路径问题.彭勇等人[8]在团队定向问题中考虑二维装箱约束条件,提出了改进的BLF算法.但在客户需求可进行拆分配送的问题中并没有学者考虑过装箱约束,需求可拆分车辆路径问题求得的目标值虽然低于车辆路径问题,但是其得到的最优路线未考虑被装货物尺寸与车厢尺寸之间的关系,往往会出现分配给一辆车的配送任务由于无法装箱而重新分配,出现重复装卸货物的现象,不仅会增加装卸成本,还降低了配送中心的服务水平.因此,对带二维装箱约束[9]的SDVRP问题进行研究显得非常重要.由于考虑二维装箱约束的需求可拆分车辆路径问题是装箱问题与需求可拆分车辆路径问题的组合,且两者都属于典型的组合优化问题,属于NP难问题,其计算复杂性已经远远超过单独求解车辆路径问题与装箱问题,本文首先建立2L-SDVRP数学模型,并在此基础上设计了以改进遗传算法作为算法框架,结合改进BLF装箱算法,能求解2L-SDVRP的启发式算法(BLF-GA算法).
1 2L-SDVRP模型建立及解的特征 1.1 2L-SDVRP模型建立2L-SDVRP可以定义为:图G=(V, E),顶点集V=(1, 2, …, n),其中:1,n表示物流中心(车辆从物流中心出发,最后回到物流中心),其余为客户需求点E={(i, j)|i, j∈V}为边集;Dij表示i和j两点之间的路线距离,也代表车辆由i行驶到j的成本;车场拥有vh辆车,每辆车的最大载重量为Q,单车最大行驶距离为Dmax;tik表示第k辆车在i点装载的需求量;qi表示每个客户点的需求量;Zi表示每个客户点需求量的单位重量.
定义ITi为客户点i所要求配送的mi个矩形物品集合;ITi中物品总重gi.ITi中物品m(Iim)的底面投影为lim(物品水平方向长度)×Wim(物品垂直方向长度)的矩形(在以下数学模型中会增加下标k表示该物品放入对应车辆).令车厢俯视图(车头在下)左下角为(0,0) 坐标原点,水平向右、垂直向上为坐标轴.设物品Iim左下角坐标为(vim,him)(在以下数学模型中会增加下标k表示该物品放入对应车辆).
定义变量:
| $\begin{array}{l} \quad \;{X_{ijk}} = \left\{ {\begin{array}{*{20}{l}} 1\\ 0 \end{array}} \right.,i \in \left\{ {1,2, \cdots ,n} \right\};j \in \left\{ {1,2, \cdots ,n} \right\};\\ k \in \left\{ {1,2, \cdots ,vh} \right\} \end{array}$ | (1) |
式(1) 中的变量取1时表示第k辆车从i点行驶到j点;反之,则为0;
模型假设:
1) 所有客户点的需求量及坐标位置均已知;
2) 同一客户点需求量可以大于1,但货物相同,即重量和尺寸相同;
3) 任意两节点间的距离对称Dij=Dji;
4) 任意两节点之间符合三角不等式Dij+Djk≥Dik;
5) 所有车辆从配送中心出发,任务完成后均返回配送中心等待下次任务.
则2L-SDVRP数学模型如下:
| $\min z = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^{vh} {{D_{ij}}{X_{ijk}}} } } $ | (2) |
| $\sum\limits_{k = 1}^{vh} {\sum\limits_{i = 2}^{n - 1} {{x_{ijk}}} } \ge 1,\forall j \in \left\{ {1,2, \cdots ,n} \right\}$ | (3) |
| $\begin{array}{l} \quad \quad \sum\limits_{i = 1}^n {{x_{ipk}}} - \sum\limits_{j = 1}^n {{x_{pjk}}} = 0,\forall p \in \left\{ {2,3,4, \cdots ,n - 1} \right\};\\ k \in \left\{ {1,2, \cdots ,vh} \right\} \end{array}$ | (4) |
| $\sum\limits_{k = 1}^{vh} {{t_{ik}}} = {q_i},\forall i \in \left\{ {2,3,4, \cdots ,n - 1} \right\}$ | (5) |
| $\sum\limits_{i = 1}^n {{t_{ik}}} {Z_i} \le Q,k \in \left\{ {1,2, \cdots ,vh} \right\}$ | (6) |
| $\begin{array}{l} \quad \quad 0 \le {v_{imk}} \le W - {w_{imk}},\forall i \in \left\{ {2, \cdots ,n - 1} \right\},m \in \\ \left\{ {1,2, \cdots ,{m_i}} \right\},k \in K \end{array}$ | (7) |
| $\begin{array}{l} \quad \quad 0 \le {h_{imk}} \le L - {l_{imk}},\forall i \in \left\{ {2, \cdots ,n - 1} \right\},m \in \\ \left\{ {1,2, \cdots ,{m_i}} \right\},k \in \left\{ {1,2, \cdots ,vh} \right\} \end{array}$ | (8) |
| $\begin{array}{l} \quad \quad {h_{imk}} + {l_{imk}} \le {h_{{i^\prime }{m^\prime }k}},\forall i,{i^\prime } \in \left\{ {2, \cdots ,n - 1} \right\},m \in \\ \left\{ {1,2, \cdots ,{m_i}} \right\},{m^\prime } \in \left\{ {1,2, \cdots ,{m_{{i^\prime }}}} \right\}k \in \{ 1,2, \cdots ,\\ vh\} ,i \ne {i^\prime } \end{array}$ | (9) |
| $\begin{array}{l} \quad \quad {v_{imk}} + {w_{imk}} \le {v_{{i^\prime }{m^\prime }k}},\forall i,{i^\prime } \in \left\{ {2, \cdots ,n - 1} \right\},m \in \\ \left\{ {1,2, \cdots ,{m_i}} \right\},{m^\prime } \in \left\{ {1,2, \cdots ,{m_{{i^\prime }}}} \right\}k \in \{ 1,2, \cdots ,\\ vh\} ,i \ne {i^\prime } \end{array}$ | (10) |
| $\begin{array}{l} \quad \quad {v_{imk}} \ge {v_{{i^\prime }{m^\prime }k}},\forall i,{i^\prime } \in \left\{ {2, \cdots ,n - 1} \right\},m \in \{ 1,\\ 2, \cdots ,{m_i}\} ,{m^\prime } \in \left\{ {1,2, \cdots ,{m_{{i^\prime }}}} \right\}k \in \left\{ {1,2, \cdots ,vh} \right\},\\ i \ne {i^\prime } \end{array}$ | (11) |
| $\begin{array}{l} \quad \quad {h_{imk}} + {l_{imk}} \le {h_{{i^\prime }{m^\prime }k}},\forall i,{i^\prime } \in \left\{ {2, \cdots ,n - 1} \right\},m \in \\ \left\{ {1,2, \cdots ,{m_i}} \right\},{m^\prime } \in \left\{ {1,2, \cdots ,{m_{{i^\prime }}}} \right\}k \in \{ 1,2, \cdots ,\\ vh\} ,i \ne {i^\prime } \end{array}$ | (12) |
| $\begin{array}{l} \quad \quad {h_{{i^\prime }{m^\prime }k}} + {l_{{i^\prime }{m^\prime }k}} \le {h_{imk}},\forall i,{i^\prime } \in \left\{ {2, \cdots ,n - 1} \right\},m \in \\ \left\{ {1,2, \cdots ,{m_i}} \right\},{m^\prime } \in \left\{ {1,2, \cdots ,{m_{{i^\prime }}}} \right\}k \in \{ 1,2, \cdots ,\\ vh\} ,i \ne {i^\prime } \end{array}$ | (13) |
| $\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{D_{ij}}{x_{ijk}}} \le {D_{\max }},k \in \left\{ {1,2, \cdots ,vh} \right\}} $ | (14) |
式(2) 给出模型优化目标为车辆行驶总路径长度最短;式(3) 表示每个客户点至少有一辆车进行配送;式(4) 表示车辆流量守恒,即车辆驶入某点完成任务后就驶出该点;式(5) 表示客户的所有需求必须完成;式(6) 表示车辆载重约束,即某条线路上车辆所服务客户的所有或部分需求对应的重量不能超过车辆的最大载重量.式(7)、式(8) 表示每条路径上物品以固定方向都能装入车内;式(9)、式(10) 表示物品不能相互叠放;式(11)~(13) 保证装箱物品能按序不受阻挡以物品装入方向直线移进移出;式(14) 为行驶距离限制.
1.2 ZL-SDVRP解的特征定理1 考虑装箱约束可行解集合⊆不考虑装箱约束可行解集合.
证明:假设R为不考虑装箱约束时的不可行解集合,r1∈R; S为不考虑装箱约束时的可行解集合,r2∈S.
1) 从2L-SDVRP模型中可知,装箱约束为模型中的式(6)~(12).r1为不考虑装箱约束时的不可行解,即r1不满足式(2)~(5) 中的任意一个约束条件或者几个,那么r1必定也为考虑装箱约束时的不可行解;
2) r2为不考虑装箱约束时的可行解,即r2满足式(2)~(5) 中的任意一个约束条件.但是考虑装箱约束后,一条配送路线上客户需求的货物不一定能全部装上车,即r2不一定是考虑装箱约束的可行解.
因此,在2L-SDVRP模型中,考虑装箱约束的可行解一定也是不考虑装箱约束的可行解.证毕.
推论1 考虑装箱约束的最优值≥不考虑装箱约束的最优值.
证明:由定理1已知考虑装箱约束可行解集合⊆不考虑装箱约束可行解集合,可得考虑装箱约束的最优解∈不考虑装箱约束可行解集合.
假设不考虑装箱约束的最优值>考虑装箱约束的最优值,那么不考虑装箱约束的最优解∉考虑装箱约束可行解集合,与考虑装箱约束可行解集合⊆不考虑装箱约束可行解集合发生矛盾,假设不成立.原命题成立.证毕.
2 BLF-GA算法BLF-GA算法是在改进的遗传算法框架上再结合BLF算法[7]设计的,算法步骤如下:
步骤1:初始化
步骤1.1调用Distanse生成客户点之间的欧式距离;
步骤1.2调用InitPop生成初始种群;
步骤2:循环
for gen=1:MAXGEN
for i=1:NIND
步骤2.1调用SDVRP得到种群中所有个体的具体路线以及路线长度(未考虑装箱约束);
end
步骤2.2调用Fitness得到最优路线长度的倒数;
步骤2.3选择操作:嵌套调用函数(第一次调用函数Select, 在Select函数中调用Sus函数)得到SelCh
步骤2.4交叉操作:将SelCh作为交叉对象调用intercross函数,更新SelCh;
步骤2.5变异操作:用rand函数随机生成0-1的小数,并与变异概率对比,确定是否变异,若发生变异,更新SelCh;
步骤2.6重插入子代的种群:为了保持种群大小不变,经过选择、交叉及变异操作后,除了SelCh,还应插入Chrom-SelCh的个体,才能保持种群的大小不变;
end(停止准则:达到最大迭代次数时停止循环)
步骤3:装箱检验
步骤3.1将上述未考虑装箱约束得到的最优路线调用zhuangxiangtest函数,检验每辆车的货物是否符合装箱(装箱时不仅要满足每条路线上客户的货物都能装上,还需满足先配送的客户货物后装以及同意顾客货物面积大的放在面积小的下方的原则).若有路线不满足装箱,则进行步骤4.
步骤4:循环
for gen=1:MAXGEN
for i=1:NIND
步骤4.1调用SDVRP得到种群中所有个体的具体路线以及路线长度(考虑装箱约束);
end
步骤4.2调用Fitness得到最优路线长度的倒数;
步骤4.3选择操作:嵌套调用函数(第一次调用函数Select, 在Select函数中调用Sus函数)得到SelCh
步骤4.4交叉操作:将SelCh作为交叉对象调用intercross函数,更新SelCh;
步骤4.5变异操作:用rand函数随机生成0-1的小数,并与变异概率对比,确定是否变异,若发生变异,更新SelCh;
步骤4.6重插入子代的种群:为了保持种群大小不变,经过选择、交叉及变异操作后,除了SelCh,还应插入Chrom-SelCh的个体,才能保持种群的大小不变;
end(停止准则:达到最大迭代次数时停止循环)
经过BLF-GA算法得到的最终结果则为2L-SDVRP的最优解.考虑到2L-SDVRP问题的复杂性,本文使用直接表示的方法对可行解进行表示,即每个解是按照车辆的访问顺序生成的,不再需要其他计算资源进行解码操作,可以降低求解的复杂度.
2.1 编码操作考虑到需求可分的特殊性,本算法直接采用自然数进行编码来形成个体,如:

|
表示含义:客户1需求为2,客户2需求为2,客户3需求为2,客户4需求为1,客户5需求为3,需求总量为10.
2.2 初始化种群采用“随机”的方法生成初始种群.
2.3 适应度评价用适应度可以评价个体的优劣.在该遗传算法中,评价公式为:E=z+Ps, 由于2L-SDVRP是求最小值问题,因此根据遗传算法对适应度函数的要求,该个体的适应度f可以用以下方法计算:
将由评价公式所得值的倒数视为个体的适应度,即:
该算法所采用的是精英选择策略.
2.5 交叉操作采用部分映射的方法,从被选择的个体中随机抽取两个个体进行交叉.为了保持各点需求量满足要求,对交叉原则进行改进如下:
例如,将染色体[5, 8]之间的元素进行交叉:
染色体a:

|
染色体b:

|
交叉后得到两个新染色体:
染色体a1:

|
染色体b1:

|
从交叉后的染色体分布可以看出:各个点的需求量不满足要求,需要做出调整,使其满足需求量.如在染色a1中客户点3的需求量多出2个单位,客户点2的需求量多出1个单位,然后客户点1、4、5都分别少了1个单位.所以随机选取客户点3和2多出的元素变为0,然后再将这些0元素用1、4、5去替补.经过交叉操作后的两个染色体为:
染色体a2:

|
染色体b2:

|
该方法可以保证群体得到新的染色体进行进化,进而得到最优解.
2.6 变异操作变异策略采取随机选取两个点,将其对换位置.例如将下面染色体进行变异:产生两个[1, 15]范围内的随机整数,确定位置,将其对换位置,如4、7两个位置.

|
变异后为:

|
为了对遗传算法的局部搜索能力进行改善,在程序执行完选择、交叉、变异操作之后引进连续多次的进化逆转操作.进行进化逆转操作后,形成的新个体,只有个体适应度值有提高的才会留下来.
产生两个[1, 10]范围内的随机整数,确定两个位置,将其对换位置,如4、8两个位置

|
进化逆转后为

|
设某配送问题有20个客户,其中编号1表示配送点.这些客户分布在x, y坐标为[0, 20]的一个区域内,车场坐标为(15, 13);进行配送服务的车辆类型相同,其中车厢长度为L=10,宽度为W=20,每辆车的载重量为10,每辆车的最大行驶距离不超过50;每个客户点的坐标以及需求量,如表 1所示.每个客户的需求单位化后对应货物投影在箱底的长度、高度如表 2所示,每个客户点所需求的货物尺寸相同.
| 编号 | X坐标 | Y坐标 | 需求量 | 单位重量 |
| 1 | 15 | 13 | 0 | 0 |
| 2 | 13 | 9 | 2 | 2 |
| 3 | 18 | 3 | 2 | 1 |
| 4 | 15 | 17 | 2 | 1 |
| 5 | 20 | 15 | 1 | 3 |
| 6 | 16 | 12 | 3 | 1 |
| 7 | 4 | 11 | 2 | 2 |
| 8 | 11 | 8 | 1 | 2 |
| 9 | 9 | 8 | 3 | 3 |
| 10 | 13 | 2 | 1 | 1 |
| 11 | 14 | 5 | 4 | 2 |
| 12 | 7 | 17 | 2 | 3 |
| 13 | 15 | 3 | 2 | 2 |
| 14 | 2 | 9 | 3 | 1 |
| 15 | 17 | 11 | 1 | 1 |
| 16 | 7 | 1 | 1 | 2 |
| 17 | 0 | 3 | 3 | 2 |
| 18 | 12 | 20 | 1 | 2 |
| 19 | 13 | 15 | 4 | 2 |
| 20 | 6 | 6 | 1 | 1 |
| 21 | 10 | 15 | 1 | 2 |
| 客户点编号 | (l, w) | 客户点编号 | (l, w) | 客户点编号 | (l, w) |
| 2 | (5, 6) | 9 | (5, 7) | 16 | (2, 13) |
| 3 | (3, 11) | 10 | (4, 4) | 17 | (3, 7) |
| 4 | (2, 4) | 11 | (4, 11) | 18 | (6, 12) |
| 5 | (5, 5) | 12 | (2, 6) | 19 | (5, 5) |
| 6 | (5, 15) | 13 | (3, 11) | 20 | (4, 11) |
| 7 | (3, 6) | 14 | (5, 4) | 21 | (3, 10) |
| 8 | (4, 9) | 15 | (3, 7) |
实验中遗传算法参数种群规模为200;进化代数取900;选择概率GGAP=0.9,交叉概率Pc=0.9,变异概率Pm=0.05;惩罚权重Ps=1000.
3.1 运行结果算法采用MATLAB实现.所有计算在操作系统Windows 7,配置为Intel(R) Pentium(R) CPU p6000@1.87GHz,2.00 GB内存电脑上完成.
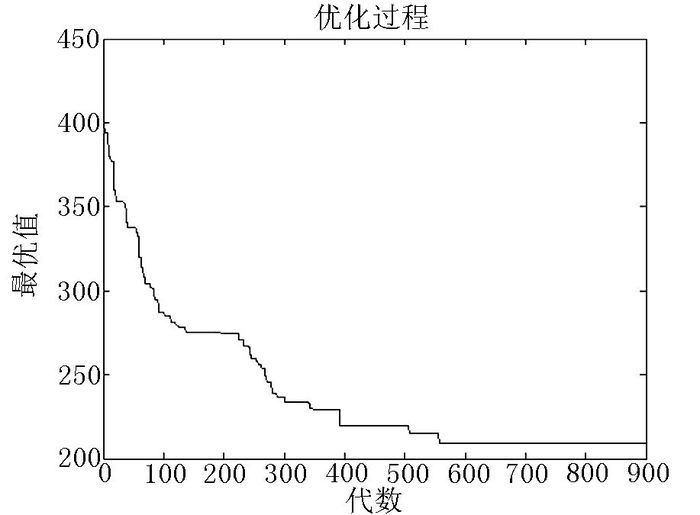
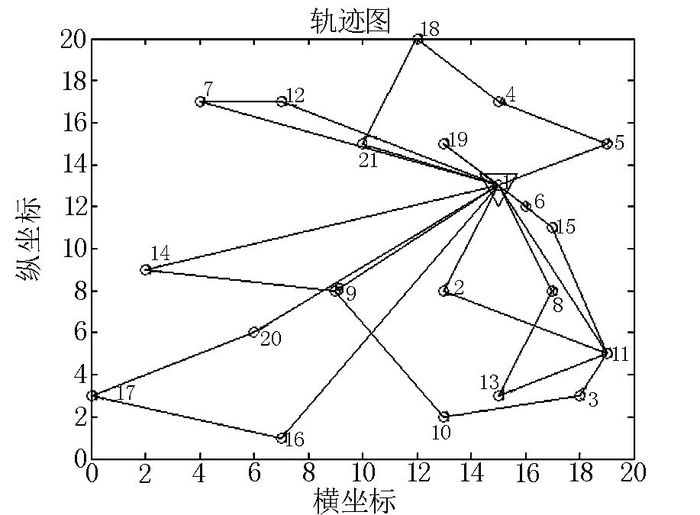
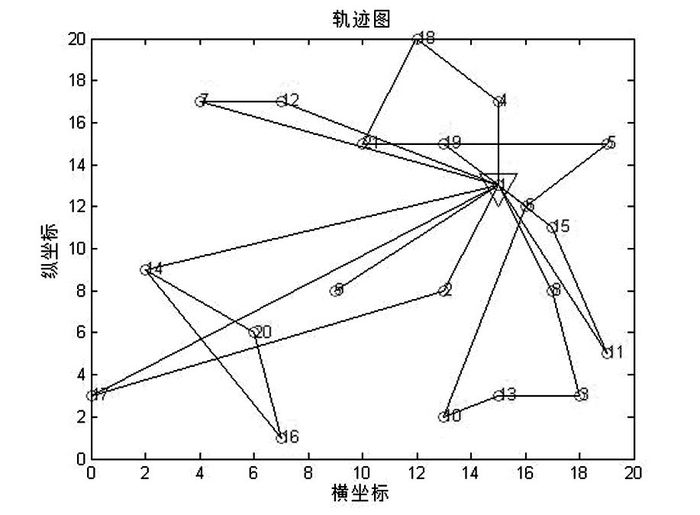
针对2L-SDVRP,分别求解考虑装箱约束和不考虑装箱时的最优值及最优路线.图 1和图 2是考虑装箱约束时的算法进化过程图和最优路线图,图 3和图 4是不考虑装箱约束时的算法进化过程图和最优路线图.表 3是考虑装箱约束与不考虑装箱约束时所得最优结果的比较,表 4是不考虑装箱约束时所得最优路线的装箱检验结果.
|
| 图 1 考虑装箱约束的进化过程图 Fig. 1 Process of algorithm with loading constraint |
|
| 图 2 考虑装箱约束的最优路线图 Fig. 2 Optimal route with loading constraint |
|
| 图 3 不考虑装箱约束的进化过程图 Fig. 3 Process of algorithm without loading constraint |
|
| 图 4 不考虑装箱约束的最优路线图 Fig. 4 Optimal route without loading constraint |
| 考虑装箱最优结果 | 不考虑装箱约束最优结果 | ||
| 路径序号 | 最优路线 | 路径序号 | 最优路线 |
| 路径1 | 1→6→19→19→1 | 路径1 | 1→9→9→9→1 |
| 路径2 | 1→8→13→13→11→15→1 | 路径2 | 1→2→2→17→17→17→1 |
| 路径3 | 1→7→7→12→12→1 | 路径3 | 1→19→19→5→6→6→1 |
| 路径4 | 1→5→4→4→18→21→1 | 路径4 | 1→19→19→21→18→4→4→1 |
| 路径5 | 1→14→14→14→9→9→1 | 路径5 | 1→14→14→16→20→14→1 |
| 路径6 | 1→2→2→11→11→1 | 路径6 | 1→15→11→11→11→11→1 |
| 路径7 | 1→6→6→19→19→1 | 路径7 | 1→7→7→12→12→1 |
| 路径8 | 1→9→10→3→3→11→1 | 路径8 | 1→8→3→3→13→13→10→6→1 |
| 路径9 | 1→16→17→17→17→20→1 | ||
| 最优值 | 209.61 | 最优值 | 202.96 |
| 路径序号 | 具体顺序 | 是否满足装箱约束 |
| 路径1 | 1→9→9→9→1 | 1 |
| 路径2 | 1→2→2→17→17→17→1 | 1 |
| 路径3 | 1→19→19→5→6→6→1 | 1 |
| 路径4 | 1→19→19→21→18→4→4→1 | 1 |
| 路径5 | 1→14→14→16→20→14→1 | 1 |
| 路径6 | 1→15→11→11→11→11→1 | 0 |
| 路径7 | 1→7→7→12→12→1 | 1 |
| 路径8 | 1→8→3→3→13→13→10→6→1 | 0 |
| 注:是否满足装箱约束一栏中“0”表示不满足装箱;“1”表示满足装箱. | ||
从表 3可以得出,当考虑装箱约束时用BLF-GA算法所得的最优值大于不考虑装箱约束时的最优值.从表 4可以得出,不考虑装箱约束时所得的最优路线中存在两条不满足装箱约束的路线:路径6和路径8.
4 结论本文研究的2L-SDVRP是二维装箱问题与需求可拆分问题的结合,并针对这个组合优化问题建立了相关的数学模型,提出了BLF-GA算法,成功求解了2L-SDVRP.通过比较2L-SDVRP中考虑装箱约束和不考虑装箱约束的运行结果,发现:当不考虑装箱约束时所得的最优路线存在不满足装箱约束的情况,并且考虑装箱约束时所得的最优值大于不考虑装箱时的最优值.考虑装箱约束得到的最优路线由于较好地处理了被装货物尺寸与车厢尺寸之间的关系,所以不会出现分配给一辆车的配送任务由于无法装箱而重新分配,最终导致出现重复装卸货物的现象,不仅使装卸成本降到最低,而且提高了配送的服务水平.
| [1] | Dantzig G., Ramser J.. The truck dispatching problem[J]. Management Seience, 1959(6): 80–91 |
| [2] | 彭勇, 谢禄江, 刘松. 时变单车路径问题建模及算法设计[J]. 重庆交通大学学报:自然科学版, 2013, 32(2): 263–266. |
| [3] | 彭勇, 何俊生. 实时路网单车多任务物流配送路径优化[J]. 重庆交通大学学报:自然科学版, 2014, 33(2): 122–125. |
| [4] | Dror. M., Trudeau. P.. Savings by split delivery routing[J]. Transportation Science 23, 1989: 141–145 |
| [5] | Frizzell P., Giffin J.. The bounded split delivery vehicle routing problem with grid network distances[J]. Asia Pacific Journal of Operational Research, 1992(9): 101–116 |
| [6] | Frizzell P., Giffin J.. The split delivery vehicle scheduling problem with time windows and grid network distances[J]. Computers & Operational Research, 1995(22): 655–667 |
| [7] | Chi-Guhn Lee, Marina A, et al. A shortest path approach to the multiple-vehicle routing problem with split pick-ups[J]. Transporation Research, 2006(40): 265–284 |
| [8] | 彭勇, 宋其勤. 带二维装箱约束的团队定向问题模型及优化算法[J]. 重庆交通大学:自然科学版, 2016, 35(3): 141–147. |
| [9] | 武晓今, 朱仲英. 二维装箱问题的一种实现方法[J]. 微型电脑应用, 2003, 19(4): 20–23. |
| [10] | Dror M, Trudeau P.. Savings by split delivery routing[J]. Transportation Science, 1989, 23(2): 141–145 DOI:10.1287/trsc.23.2.141. |
| [11] | Dror M, Trudeau P. Split delivery routing[J]. Naval Research Logistics, 1994, 50(3): 239–254 |
 2017, Vol. 23
2017, Vol. 23