在实际生活中,许多问题都可以转化为数学优化问题。过去几十年,由于越来越复杂的数学优化问题亟待解决,使得学者提出各种各样的优化算法,其中,群智能算法得到了很大发展。群智能算法在多年实践中展现了相对于传统数学规划方法更大的优势[1], 尤其是在无法求解梯度的优化问题中得到了长足发展。集约化和多元化是群智能算法的两个主要特点[2],较为流行的群智能算法有粒子群算法[3](PSO)、差分进化算法(DE)[4]和蚁群算法(ACO)[5]等,这些算法已广泛应用于车间调度问题[6]、路径最短优化问题[7]、化工过程优化问题[8~10]等,并取得了良好的效果。飞蛾火焰优化算法[11](MFO)由澳大利亚学者Mirjalili提出的一种新的启发式算法,该算法受到自然界中飞蛾根据光线方向横向移动特性的启发而提出。
飞蛾火焰优化算法中的飞蛾和火焰均为优化问题的搜索因子,由于飞蛾是按照螺旋曲线轨迹向火焰靠拢,因此,仅用较少的计算成本就可覆盖到更广的未知空间,但是该算法和其他启发式算法类似,在迭代后期由于其螺旋式运行轨迹的原因,使其很容易陷入局部最优。针对MFO算法的这一缺点,本文加入多策略扰动机制,通过莱维飞行和布朗运动两种不同扰动机制的组合,使得飞蛾粒子能够搜索更广的空间,具备更强的探索力和收敛性。
聚乙烯是由单体乙烯聚合生成的高聚物,广泛应用于薄膜、拉丝、管材制造等方面[12]。目前,聚乙烯的生产主要通过催化剂在低压环境下进行生产,有溶液法、淤浆法、气相法[13]三种工艺[14]。但是,不同催化剂催化乙烯聚合反应动力学参数差异明显,在建模过程中,其反应动力学参数的确定是个难点。因此,本文以气相法生产过程模型为对象,以聚乙烯的数均分子量和重均分子量为目标,利用基于多策略扰动的飞蛾火焰算法调节动力学参数,使得模型输出的数均分子量和重均分子量与实际工况输出值之间的相对误差平方和最小。
2 飞蛾火焰优化算法飞蛾火焰算法是通过飞蛾在夜间朝着灯光螺旋飞行的习性而推演出的一种群智能算法。飞蛾火焰算法中的飞蛾和火焰均是问题的搜索解,它们的不同之处是对其训练和更新的机制不同。
可以将飞蛾火焰优化算法归纳为如下几个步骤:
初始化阶段:初始化最大迭代次数T、种群规模n、优化问题维度d,并随机初始化种群的位置得到矩阵Mn×d作为初始飞蛾矩阵。得到初始种群的适应度数组OM并按适应度对飞蛾矩阵进行排序得到新的矩阵Fn×d作为初始火焰矩阵。
第一次迭代:
| $ S({M_i},{F_j}) = {D_i} \cdot {{\text{e}}^{bt}} \cdot \cos (2\pi t) + {F_j} $ | (1) |
其中,
第l次迭代:将第l-1次迭代结果中适应度更好的飞蛾替换掉适应度较差的火焰以更新火焰种群,然后按式(1)进行第l次迭代更新飞蛾种群。重复该迭代过程,直到迭代结束。
在迭代的过程中,火焰种群的数量按式(2)进行递减:
| $ \text{flame}\_\text{no}=\text{round}\left( n-l\times \frac{n-1}{T} \right) $ | (2) |
火焰数量的递减是为了迭代后期加速种群的收敛。迭代过程中,火焰粒子的数量越来越少,飞蛾粒子的数量相对会有“多余”,这时让“多余”的飞蛾绕最优火焰进行旋转更新。
3 辅助寻优机制 3.1 布朗运动布朗运动是英国植物学家布朗通过花粉实验而得到的结论。布朗运动有两个主要的特点:微粒质量越小,运动越激烈;温度越高,粒子运动越激烈[15]。气体粒子的运动速度可用下式表示:
| $ v = \sqrt {\frac{{3K{T_0}}}{m}} $ | (3) |
其中,K为玻尔兹曼常数,T0为温度,m为粒子质量。
3.2 莱维飞行莱维分布是法国数学家莱维于上世纪30年代提出的一种概率分布,并以他的名字命名,许多动物的觅食轨迹被证明是符合莱维分布的[16]。莱维飞行是符合莱维分布的搜索规则,其行走的步长满足重尾的特点。这种满足莱维概率分布的莱维飞行会出现一种在附近进行数次短距离步行后会有远距离甚至超远距离跳跃的现象。
莱维飞行可以用如下公式计算:
| $ L = 0.01 \times \frac{{{r_1} \times \sigma }}{{{{\left| {{r_2}} \right|}^{\frac{1}{\beta }}}}} $ | (4) |
其中,r1, r2是属于0到1之间的随机数,β是一个常数,σ可用如下公式计算:
| $ \sigma = {\left( {\frac{{\mathit{\Gamma} (1 + \beta ) \times \sin \left( {\frac{{\pi \beta }}{2}} \right)}}{{\mathit{\Gamma} \left( {\left( {\frac{{1 + \beta }}{2}} \right) \times \beta \times {2^{\frac{{\beta - 1}}{2}}}} \right)}}} \right)^{\frac{1}{\beta }}} $ | (5) |
其中,
目前,大多数的研究者对超越可行空间粒子的处理方法是将超限粒子拉回最近边界,但对于大多数优化问题,其最优点并非在边界上取得,这样就会导致拉回边界的粒子并没有对最优解的寻找起到实质性作用,因此,本文提出超限概率反弹机制,将超越界限的粒子部分反弹回可行空间内部。超限概率反弹机制如下:
| $ {x_{{\text{new}}}} = \left\{ \begin{gathered} ub\;,\quad \quad \quad \quad \quad \quad \quad \quad \quad x > ub\& {\text{rand}} > 0.7 \hfill \\ ub - {\text{mod}}(x - ub,\;ub - lb)\,,\,x > ub\& {\text{rand}} < 0.7 \hfill \\ lb\,,\quad \quad \quad \quad \quad \quad \quad \quad \quad \;{\kern 1pt} x < lb\& {\text{rand}} > 0.7 \hfill \\ lb + {\text{mod}}(lb - x,\;ub - lb)\,,\;\;{\kern 1pt} x < lb\& {\text{rand}} < 0.7 \hfill \\ \end{gathered} \right. $ | (6) |
其中,ub, lb分别为可行空间某一维度的上限和下限,x为原粒子在该维度的位置,xnew为粒子在该维度通过上式更新后的新位置。
4 改进的飞蛾火焰算法通过上节介绍可以看出,飞蛾火焰算法相对于其他群智能算法有明显的优势,由于其螺旋运行规则,仅仅通过调节较少参数就可以使飞蛾种群覆盖到更大范围的搜索空间。但是,飞蛾火焰优化算法存在比较明显缺陷,在对飞蛾进行更新时是对飞蛾粒子的每一维通过式(1)进行的,假如飞蛾粒子和对应火焰粒子的某些维度位置相同或接近,那么在更新的过程中,飞蛾粒子只能在可行空间的某一个低维超平面内更新,使得粒子搜索空间相对于原来可行空间大大减小,在迭代后期尤为严重,很容易陷入局部范围甚至只在低维空间搜索直到迭代结束。
Bhesdadiya[17]通过对PSO和MFO算法结合,提出了HPSO-MFO算法,利用MFO算法通过较少的计算成本可覆盖更广的未知搜索空间区域以及PSO算法避开局部最优的能力来提高算法的寻优精度。本文提出基于多策略扰动机制的飞蛾火焰算法,在飞蛾粒子通过式(1)更新之后,选择部分粒子进行莱维飞行扰动,而另外一些粒子进行布朗运动扰动。迭代前期,通过布朗运动被扰动的粒子可行空间更大,保证了飞蛾粒子在前期的全局搜索。随着迭代次数的增加,布朗运动扰动的范围越来越小,保证局部的探索能力,而由于莱维飞行有长距离跳跃的特点,被莱维飞行机制扰动粒子中的大部分在其附近移动,少部分会长距离跳跃到其他区域,从而增加了跳出局部最优的概率。通过两种策略的混合扰动,便可增加种群的多样性及后期的搜索能力。
为了使布朗运动机制适合本文算法改进策略,设单步布朗运动扰动
| $ {P_b} = (ub - lb)\sqrt {\frac{{{T_0}}}{m}} \cdot {\text{Gaussian}}(0,1) $ | (7) |
其中,ub为可行空间的上界,lb为可行空间的下界,m=iteration随着迭代次数的增加而增大,T0为自定义常数,本文设为0.25。上式可以转换为如下形式:
| $ {P_b} = 0.5\frac{{ub - lb}}{{\sqrt {iteration} }} \cdot {\text{Gaussian}}(0,1) $ | (8) |
改进后的飞蛾火焰算法的具体流程如下:
初始化阶段:初始化最大迭代次数T、种群规模n、优化问题维度d,并随机初始化种群的位置得到矩阵Mn×d作为初始飞蛾矩阵。得到初始种群的适应度数组OM并按适应度对飞蛾矩阵进行排序得到新的矩阵Fn×d作为初始火焰矩阵。
第一次迭代:
| $ {\text{rand}} < l/T $ | (9) |
rand为符合[0, 1]均匀分布的随机数。当符合式(9)时,采用莱维飞行扰动,否则,采用布朗运动扰动。
第l次迭代:将第l-1次迭代结果中适应度更好的飞蛾替换掉适应度较差的火焰以更新火焰种群,然后按式(1)进行第l次迭代更新,更新之后的飞蛾粒子按式(9)进行随机选择扰动机制并重新定位。重复该迭代过程直到迭代结束。
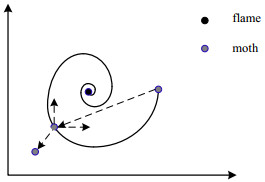
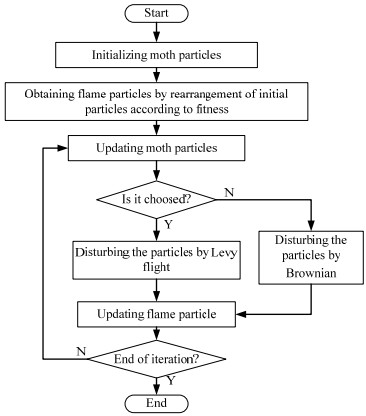
迭代过程中,火焰数量按式(2)递减。改进后飞蛾火焰算法的飞蛾更新如图 1所示。基于多策略扰动机制的飞蛾火焰算法整个迭代流程如图 2所示。
|
图 1 飞蛾粒子单次迭代规则 Fig.1 Single iteration rule of the moth particle |
|
图 2 多策略扰动飞蛾火焰算法流程图 Fig.2 Flow chart of the MSMFO algorithm |
为验证本文提出的基于多策略扰动的飞蛾火焰算法(MSMFO)有效性,选用8个经典的测试函数进行测试,测试函数的具体指标如表 1所示。
|
|
表 1 测试函数 Table 1 Benchmark functions used in the study |
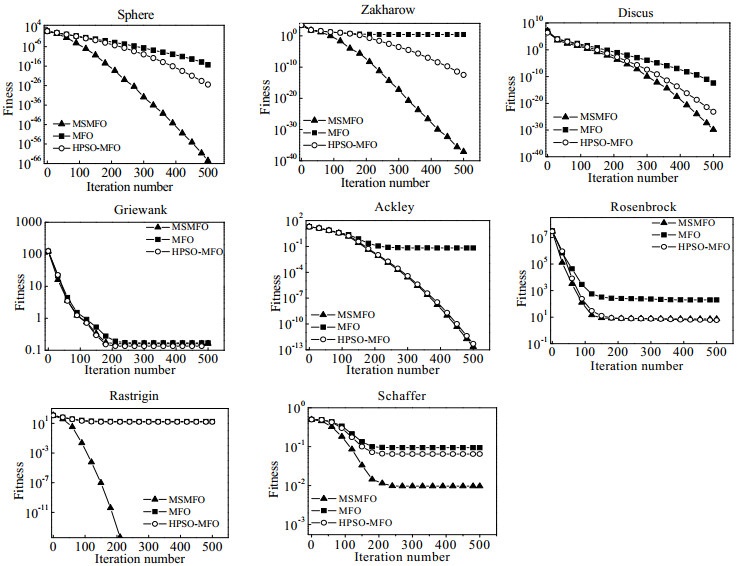
在该实验中,算法的种群数量设为50,迭代次数设为500。为了保证精度优先的原则,不设置寻优精度,直到达到最大迭代次数为止。测试函数设为10维,独立运行30次,并取平均值、标准值作为评价指标。8个标准测试函数的测试结果见表 2,MSMFO算法、HPSO-MFO算法和MFO算法的进化曲线比较见图 3。
|
|
表 2 MSMFO与HPSO-MFO、MFO测试结果 Table 2 Results of MSMFO, HPSO-MFO and MFO for benchmark functions |
|
图 3 MSMFO、HPSO-MFO和MFO在各测试函数上进化曲线比较 Fig.3 Profiles of MSMFO, HPSO-MFO and MFO for different benchmark functions |
从表 2中可以看到,在各个测试函数上的测试结果中,MSMFO均表现更佳,收敛精度有较大的提高,其标准差也明显减小,说明MSMFO算法具有更好的稳定性。
从图 3也可以直观地看出,经过一定的迭代次数后,MFO算法的种群最优值下降速度明显减慢,种群的活性降低,很快陷入了局部最优而无法跳出,而加入多策略扰动机制的飞蛾火焰算法在前期为了达到覆盖整个可行空间的目的,而到迭代后期,由于莱维飞行策略的加入,增加了跳出局部最优的概率,而又由于布朗运动扰动的范围越来越小,其局部目标探索能力增强,寻优精度迅速提高。
5.2 MSMFO与其他算法的优化性能比较MSMFO算法除了与MFO算法比较外,还与ELPSO算法[18]、DE算法[19]、CS算法[20]等在优化问题中应用较广的算法进行比较。初始化种群规模均设为50个,最大迭代次数设为500次。为防止单次结果的偶然性,本文将以上五种算法在测试函数上独立运行30次,取各自的结果平均值及标准差作为评价指标。对测试函数的维数分别设为30维、50维两种情况进行测试。
从表 3可见,在30维和50维的测试函数运行结果中,MSMFO算法相较于其他算法具有明显的优势。在测试标准一致的情况下,收敛精度优于其他算法。
|
|
表 3 30维、50维函数上的算法性能比较 Table 3 Comparison of different algorithms under 30 and 50-dimensional functions |
气相法聚乙烯生产工艺,由于其生产过程简单,总的转化成本与高压聚乙烯装置的转化成本相比要低得多,因此该方法所生产的聚乙烯占聚乙烯总产量的比重越来越大。气相法聚乙烯的生产过程中需要的原料有单体乙烯、共聚单体丁烯、氢气、催化剂、助催化剂等。
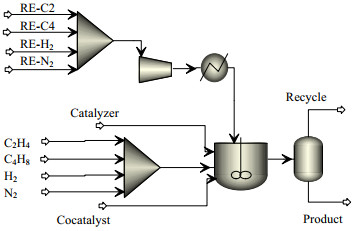
Aspen Plus软件在化工过程模拟中应用越来越广泛,本文通过Aspen Plus软件进行建模,具体模型如图 4所示。为了便于模拟,将循环回路进行断流操作,以循环回路中的乙烯、丁烯、氢气流速以及新鲜乙烯、丁烯、氢气进料流量、催化剂进料量、助催化剂进料量和反应器的温度、压力为操作变量。
|
图 4 聚乙烯生产模拟流程图 Fig.4 Flow chart of the polyethylene production process |
以某石化企业为背景,聚合工艺采用联碳公司的Unipol技术,实际工况为依据,乙烯聚合过程使用催化剂为齐格勒-纳塔催化剂,助催化剂为三乙基铝。通过实验分析催化剂含有4个活性位,模拟过程中为了简化模型,反应器采用全混釜反应器,开发环境为Aspen Plus,物性方法以PC-SAFT方程[21]为基准,按照4个活性位的动力学机理进行建模,动力学机理如表 4所示。表中M1, M2分别代表乙烯和丁烯单体,Pn, i代表链长为n、末端基团为Mi的聚乙烯链段。由于催化剂含有4个活性位,因此表中j取1、2、3、4。
|
|
表 4 乙烯聚合动力学机理 Table 4 Kinetic mechanism of ethylene polymerization |
动力学常数的表达式为:
| $ k = {k_0}{{\text{e}}^{ - \frac{{{E_a}}}{{RT}}}} $ | (10) |
活化能Ea的单位为kcal·mol-1,链增长动力学反应的活化能为9 kcal·mol-1,链转移动力学反应的活化能为14 kcal·mol-1,主要通过调节指前因子k0来调整动力学常数。
由于链失活主要影响聚乙烯的产率,链终止动力学和其他动力学耦合性较低,可首先通过调节链终止动力学参数以符合产率要求,而根据文献可认为链引发动力学常数和链增长动力学常数一致[22],链增长动力学常数和链转移至氢气的动力学常数对聚乙烯分子量影响最大,本文主要针对链增长和链转移至氢气动力学常数进行调节[23]。优化算法采用MSMFO算法,开发环境为MATLAB,然后建立MATLAB和Aspen Plus之间的通信,选择三个不同工况条件。通过改进的飞蛾火焰算法调节Aspen模型中的链增长和链转移动力学参数,使目标函数值达到最小。
以三个工况下产生的聚乙烯的数均分子量和重均分子量与模型输出值之间的相对误差平方和为目标,其中表 5为主要工况数据,目标函数如式(11)所示:
| $ f = \min \sum\limits_{i = 1}^3 {\left\{ {{{\left( {\frac{{{\text{MW}}{{\text{N}}_{{\text{cal}}}} - {\text{MW}}{{\text{N}}_{{\text{real}}}}}}{{{\text{MW}}{{\text{N}}_{{\text{real}}}}}}} \right)}^2}\left. { + {{\left( {\frac{{{\text{MW}}{{\text{W}}_{{\text{cal}}}} - {\text{MW}}{{\text{W}}_{{\text{real}}}}}}{{{\text{MW}}{{\text{W}}_{{\text{real}}}}}}} \right)}^2}} \right\}} \right.} $ | (11) |
|
|
表 5 工况数据 Table 5 Working conditions |
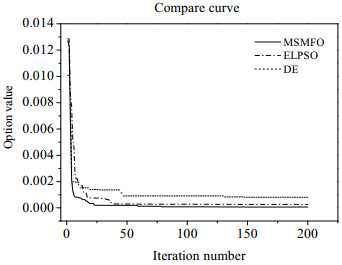
算法参数设置:种群规模设为30,最大迭代次数设为200。为了便于比较MSMFO的优化效果,选取上文的ELPSO、DE与该算法进行比较。独立运行5次,取其平均值。进化曲线如图 5所示。
|
图 5 乙烯聚合模型动力学参数优化过程 Fig.5 Optimization of model parameters for ethylene polymerization |
ELPSO和DE算法,MSMFO寻优精度已经达到10-5级别,而ELPSO寻优到达了10-4级别,DE的寻优精度更差。最终可以验证MSMFO算法的有效性。所得反应动力学指前因子参数见表 6。
|
|
表 6 模型动力学参数估计结果 Table 6 Results of model kinetic parameter |
针对飞蛾火焰算法(MFO)收敛过快以及粒子更新机制上的缺陷,提出了基于多策略扰动机制的飞蛾火焰算法(MSMFO),增加了莱维飞行和布朗运动两种扰动机制。在迭代前期通过主要依靠布朗运动的大范围扰动使得飞蛾粒子分散的更广泛,而在迭代后期通过布朗运动机制局部寻优,通过莱维飞行增加跳出局部最优的概率。在仿真阶段,对具有代表性的8个测试函数进行了仿真验证,结果证明MSMFO算法在收敛精度以及稳定性方面均表现出比较明显的优势。最后,本文将MSMFO算法用于乙烯聚合过程模型的动力学参数估计上,以提高模型的准确性,验证了MSMFO算法在工业过程建模中的有效性。
| [1] | Yang X S. Nature-inspired metaheuristic algorithms[M].Beckington: Luniver Press, 2008. |
| [2] | Gandomi A H, Yang X S, Alavi A H. Cuckoo search algorithm:a metaheuristic approach to solve structural optimization problems[J]. Engineering with Computers, 2013, 29(1): 17-35. DOI:10.1007/s00366-011-0241-y. |
| [3] | Kennedy J, Eberhart R. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Perth: IEEE Publications, 1995: 1942-1948. |
| [4] | Storn R, Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Kluwer Academic Publishers, 1997, 11(4): 341-359. |
| [5] | Colorni A, Dorigo M, Maniezzo V. Distributed optimization by ant colonies[C]//Proceedings First European Conference on Artificial Life. Paris: Elsevier, 1991: 134-142. |
| [6] | Zhang R, Song S, Wu C. A hybrid differential evolution algorithm for job shop scheduling problems with expected total tardiness criterion[J]. Applied Soft Computing, 2013, 13(3): 1448-1458. DOI:10.1016/j.asoc.2012.02.024. |
| [7] | Ghoseiri K, Nadjari B. An ant colony optimization algorithm for the bi-objective shortest path problem[J]. Applied Soft Computing, 2010, 10(4): 1237-1246. DOI:10.1016/j.asoc.2009.09.014. |
| [8] | Chen X, Du W, Qian F. Multi-objective differential evolution with ranking-based mutation operator and its application in chemical process optimization[J]. Chemometrics and Intelligent Laboratory Systems, 2014, 136(16): 85-96. |
| [9] | Qian F, Sun F, Zhong W M, et al. Dynamic optimization of chemical engineering problems using a control vector parameterization method with an iterative genetic algorithm[J]. Engineering Optimization, 2013, 45(9): 1129-1146. DOI:10.1080/0305215X.2012.720683. |
| [10] | CHEN Jia-xing(陈家星), CUI Guo-min(崔国民), ZHU Yu-shuang(朱玉双), et al. Optimization of heat exchanger network with improved firefly algorithm(改进萤火虫算法应用于换热网络最优化)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2017, 31(1): 170-178. DOI:10.3969/j.issn.1003-9015.2017.01.024. |
| [11] | Mirjalili S. Moth-flame optimization algorithm:a novel nature-inspired heuristic paradigm[J]. Knowledge-Based Systems, 2015, 89(1): 228-249. |
| [12] | SHEN Hang (沈航). ASPEN modeling of slurry polyethylene production process (淤浆聚乙烯生产流程ASPEN建模)[D]. Hangzhou (杭州): Zhejiang University (浙江大学), 2005. |
| [13] | YANG Bao-zhu(杨宝柱), JIANG Wei(江炜), WANG Jing-dai(王靖岱), et al. Simulation of particle size distribution in gas phase ethylene polymerization fluidized-bed reactor(气相流化床聚乙烯颗粒粒径分布模型的研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2005, 19(4): 461-467. DOI:10.3321/j.issn:1003-9015.2005.04.007. |
| [14] | LV Guo-lin(吕国林), ZHANG Ming(张明). Comparison and selection of polyethylene production technology(聚乙烯生产技术比较与选择)[J]. Petrochemical Technology and Application(石化技术与应用), 2003, 21(3): 190-195. DOI:10.3969/j.issn.1009-0045.2003.03.011. |
| [15] | Abdechiri M, Meybodi M R, Bahrami H. Gases Brownian motion optimization:an algorithm for optimization (GBMO)[J]. Applied Soft Computing, 2013, 13(5): 2932-2946. DOI:10.1016/j.asoc.2012.03.068. |
| [16] | Brown C T, Liebovitch L S, Glendon R. Lévy flights in dobe ju/'hoansi foraging patterns[J]. Human Ecology, 2007, 35(1): 129-138. DOI:10.1007/s10745-006-9083-4. |
| [17] | Jangir P, Jangir N, Kumar A, et al. A novel hybrid approach particle swarm optimizer with moth flame optimizer algorithm[C]//Advances in Computer and Computational Sciences Advances in Intelligent Systems and Computing. Singapore: Springer, 2016: 569-577. |
| [18] | Jordehi A R. Enhanced leader PSO (ELPSO):a new PSO variant for solving global optimization problems[J]. Applied Soft Computing, 2015, 26(26): 401-417. |
| [19] | Ronkkonen J, Kukkonen S, Price K V. Real-parameter optimization with differential evolution[C]//IEEE Congress on Evolutionary Computation. Edinburgh: IEEE Publications, 2005: 506-513. |
| [20] | Yang X S, Deb S. Cuckoo search via Lévy flights[C]//World Congress on Nature & Biologically Inspired Computing (NaBIC2009). Coimbatore: IEEE Publications, 2009: 210-214. |
| [21] | GU Xue-ping(顾雪萍), WANG Jia-jun(王嘉骏), SHEN Hang(沈航). Physical properties computation of pure components for ethylene slurry polymerization system(乙烯淤浆聚合体系组分的物性计算方法)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2007, 21(5): 729-733. DOI:10.3321/j.issn:1003-9015.2007.05.001. |
| [22] | Ju Y K, Choi K Y. Modeling of particle segregation phenomena in a gas phase fluidized bed olefin polymerization reactor[J]. Chemical Engineering Science, 2001, 56(13): 4069-4083. DOI:10.1016/S0009-2509(01)00078-1. |
| [23] | JIN You-shun (靳由顺). Development of new polyethylene based on Polymer Plus (基于Polymer Plus的聚乙烯新产品开发)[D]. Hangzhou (杭州): Zhejiang University (浙江大学), 2005. |




