2. 中国石化安全工程研究院 化学品安全控制国家重点实验室,山东 青岛 266071;
3. 山东齐旺达集团石油化工有限公司,山东 临淄 255400
2. State Key Laboratory of Safety and Control for Chemicals, SINOPEC Qingdao Research Institute of Safety Engineering, Qingdao 266071, China;
3. Shandong Qiwangda Group Petrochemical Co. Ltd., Linzi 255400, China
化工生产是一种涉及复杂物理变化和苛刻化学反应的过程,存在人为误操作、设备异常等引起的多种可能异常状况。如果忽视异常状况发展,轻则导致系统瘫痪,重则发生火灾、爆炸等灾难性事故,所以针对化工过程进行异常检测与识别十分必要[1]。
近年来,异常检测与识别技术快速发展,已被广泛应用于化工生产过程监控。基于数据驱动的异常检测与识别技术受到学术界的广泛关注,例如主成分分析(principal component analysis, PCA)[2-3]和k近邻算法[4]等,但是以上方法大多是基于浅层知识,难以学习到数据的深层次特征[5]。深度学习[6-7]由于基于深层次的抽象性而拥有更好的特征表示能力,其中卷积神经网络(convolutional neural network, CNN)[8]通过卷积操作学习工艺过程的特征进而构建高精度的异常识别模型,已被成功应用于化工过程异常检测与识别工作[9-10]。异常识别方法假设源域(训练数据)和目标域(测试数据)服从同一分布[11],因此不适用于时刻处于动态平衡的化工过程。YANG等[12]最早提出了边缘分布自适应的方法,该方法缩短了不同域数据的边缘分布距离。SAITO等[13]利用条件分布自适应的方法减少了不同域数据的条件分布距离。LONG等[14]提出了联合分布自适应(joint distribution adaptation, JDA)方法,同时考虑了边缘概率分布和条件概率分布。LI等[15]提出多层域联合自适应的方法,应用于轴承故障诊断中准确度达到90%。后续相关工作均是在JDA的基础上添加额外损失项,如平衡边缘分布和条件分布权重[16]、类内距和类间距[17]、结构不变性控制[18]、标签持久化[19]和流形对齐[20]等。但以上工作存在2个问题:第1,直接对原始数据进行分布适配,未能有效构建过程的机理特征[21];第2,主要通过浅层网络学习数据特征,其有限的表示能力和低泛化能力,使其不能获得高度抽象和鲁棒的特征表示。
本文提出一种面向多工况的深层机理特征自适应与深度卷积神经网络(deep mechanism feature adaptation-deep convolutional neural network, DMFA-DCNN)的异常识别方法,并针对化工过程中常见的精馏单元进行了应用。首先,为弥补现有方法直接针对原始数据进行分布适配的缺陷,提出一种新的机理学习自适应模式。构建研究对象的机理模型,学习并自适应机理模型的特征分布,解决化工过程中源域和目标域机理特征分布不一致的问题,使异常识别过程中数据服从同一分布。其次,为解决浅层学习不能获得高度抽象和鲁棒的数据特征问题,采用卷积神经网络分层抽取化工机理模型深层次特征。最后,将本方法应用于脱丙烷精馏塔工业仿真案例。
2 基于DMFA与深度学习的异常识别模型化工过程是一个强非线性的动态过程,数学建模复杂度高,求解数学模型计算量大,故采用深度学习网络学习化工过程的输入和输出,实现知识自动获取、表示和推理[22]。化工过程系统的物料衡算方程和能量衡算方程代表了与系统有关的定量关系方程组,可用于构造工艺机理特征。根据所研究的实际化工过程,建立所研究过程的物料衡算方程和热量衡算方程,并定义物料衡算方程和热量衡算方程的各项可测变量值作为深度学习模型输入,网络输入层节点数设置为物料衡算方程和热量衡算方程参数项的个数。激活函数的非线性映射近似了衡算方程的求解过程,通过深卷积层、池化层和非线性激活函数层映射输入层变量值,以获取物料衡算方程和热量衡算方程的定量关系。这些定量关系以多元组标记的形式表示,如式(1)所示。
| ${\rm (entit{y_1},entit{y_2}, \cdots ,entity}{_m},{\rm relation}{_j},{\rm entit{y_1},entit{y_2}, \cdots ,entity}{_n})$ | (1) |
其中,实体表示物料衡算方程和热量衡算方程的各项可测变量值,关系表示各项变量值所建立的符合物料衡算和热量衡算守则的等式关系,m 表示等式左边项的个数,n 表示等式右边项的个数。
针对研究对象的各项实体,构建分层物料衡算方程和热量衡算方程特征提取模型。其中,卷积层通过a个卷积核学习实体的a个特征,各卷积层的输出形式如式(2)所示。
| $h_{ij}^k = f\left( {{{\left( {{W^k} \times x} \right)}_{ij}} + {b_k}} \right)$ | (2) |
其中,f(x)代表激活函数,Wk代表连接第k个特征图的核权重,bk代表该特征图的偏置。
假设输入实体的形式为1×m×1,在步长s、填充为p的状态下,经过时域窗口n×1的卷积核进行卷积特征提取,由CNN输出式(3)得到特征图形式为1×z1×a,其中z1 = (m-n+2p)/s+1。
| ${y_i} = \sum\limits_i^{(m - n + 2p)/s + 1} {{W_i}{x_i} + b} $ | (3) |
然后,最大池化层通过池化窗口q×1、步长s的参数依次滑过特征图 1×z1×a,以滑过各个窗口的最大值组成新的特征图 1 ×z2×a,其中z2的计算方法与z1相同。
最终,采用激活函数非线性映射新获取的特征图,以增加整个网络的表达能力。本文采用ReLU (rectified linear unit)激活函数,ReLU本质上是一个分段函数,其定义如式(4)所示。
| ${\rm{rectifier}}\left( x \right) = {\rm{max}}\left\{ {0,x} \right\} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} x&{\begin{array}{*{20}{c}} {if}&{x \geqslant 0} \end{array}} \end{array}} \\ {\begin{array}{*{20}{c}} 0&{\begin{array}{*{20}{c}} {if}&{x < 0} \end{array}} \end{array}} \end{array}} \right.$ | (4) |
经过卷积、池化和非线性激活函数映射等一系列操作,逐层抽象机理模型实体的深层语义特征。针对多工况的化工过程,通过最大均值距离(maximum mean discrepancy, MMD)实现最小化源域和目标域的边缘概率分布P和条件概率分布Q,最终设计了DMFA方法。P和Q通过找到两个耦合投影矩阵As和At获得新数据表示,具体如式(5)和(6)所示。
| $\min D({P_{\rm{s}}},{P_{\rm{t}}}) = \mathop {\min }\limits_{{{{\mathit{\boldsymbol{A}}}}{_\rm s}},{{{\mathit{\boldsymbol{A}}}}{_\rm t}}} \left\| {\frac{1}{{{n_{\rm{s}}}}}\sum\limits_{{x_i} \in {{{\mathit{\boldsymbol{X}}}}{_\rm s}}} {A_{{_\rm s}}^{\rm T}{x_i}} - \frac{1}{{{m_{\rm{t}}}}}\sum\limits_{{x_j} \in {{{\mathit{\boldsymbol{X}}}}{_\rm t}}} {A_{{_\rm t}}^{\rm T}{x_j}} } \right\|_{\rm H}^2$ | (5) |
| $\min D({Q_{\rm{s}}},{Q_{\rm{t}}}) = \mathop {\min }\limits_{{{{\mathit{\boldsymbol{A}}}}{_\rm s}},{{{\mathit{\boldsymbol{A}}}}{_\rm t}}} \sum\limits_{c = 1}^C {\left\| {\frac{1}{{n_{\rm{s}}^{{\rm{(}}c{\rm{)}}}}}\sum\limits_{{x_i} \in {{\mathit{\boldsymbol{X}}}}{_\bf s}^{({{\mathit{\boldsymbol{c}}}})}} {A_{{_\rm s}}^{\rm T}{x_i}} - \frac{1}{{m{_\rm t}^{{\rm{(}}c{\rm{)}}}}}\sum\limits_{{x_j} \in {{\mathit{\boldsymbol{X}}}}{_\rm t}^{({{\mathit{\boldsymbol{c}}}})}} {A_{{_\rm t}}^{\rm T}{x_j}} } \right\|_{\rm H}^2} $ | (6) |
其中,D(x)代表最大均值距离;ns代表源域样本数;Xs代表源域样本矩阵;mt代表目标域样本数;Xt代表目标域样本矩阵;C代表类别数。
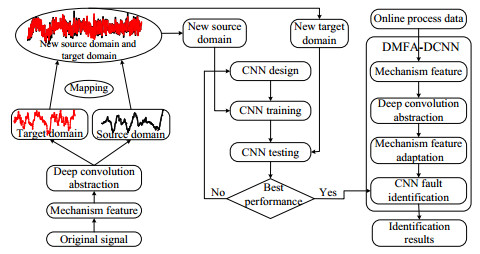
DMFA-DCNN方法分为2个阶段:离线训练阶段和在线识别阶段,如图 1所示。
|
图 1 基于DMFA-DCNN的异常识别模型 Fig.1 Anomaly identification model based on DMFA-DCNN |
第1阶段是离线训练阶段,主要实现步骤如下:
(1) 根据历史运行数据建立研究对象的物料衡算方程和热量衡算方程,从而确定式(1)中各实体值;
(2) 通过卷积(式(2))、池化(式(3))和非线性激活函数映射(式(4))等操作层层抽取物料衡算方程和热量衡算方程各项实体值特征;
(3) 将抽取的特征划分为源域和目标域;
(4) 同时适配源域和目标域的P(式(5))和Q(式(6)),以获得最小化MMD时的As和At;
(5) 通过As和At将源域和目标域变换为新源域和新目标域;
(6) 定义DCNN的超参数。
(7) 为有效测试模型的泛化性,新目标域仅用于测试识别模型,新源域用于训练识别模型。若模型达到最佳性能则保存模型,否则重新调整模型超参数。
第2阶段是在线识别阶段。该阶段实时获取化工过程的运行数据,采用建立的DMFA-DCNN模型实时识别过程数据状态。
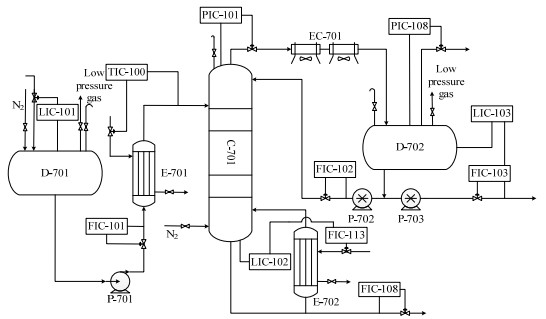
3 案例分析 3.1 脱丙烷精馏塔将DMFA-DCNN方法应用于某工业仿真脱丙烷精馏塔。脱丙烷塔作为气体分馏装置的一部分,主要用于分离催化裂化装置的液化石油气中的C2、C3及C4组分,工艺流程如图 2所示。
|
图 2 脱丙烷精馏塔工艺流程图 Fig.2 Flow diagram of depropanization distillation process |
根据脱丙烷塔的工艺流程建立了全塔的热量衡算(式(7))和物料衡算(式(8))。
| $ F{I_\rm F} + {Q_\rm F} + {Q_\rm B} = D{I_\rm D} + W{I_\rm W} + {Q_\rm C} $ | (7) |
| $\sum\limits_{i = 1}^9 {{F_i}{x_{{F_i}}}} = \sum\limits_{i = 1}^9 {{D_i}{x_{{D_i}}} + {W_i}{x_{{W_i}}}} $ | (8) |
其中F为原料液流量,kmol·h-1;IF为进料焓,kJ·kmol-1;QF为进料加热器输入热量,kJ·h-1;QB为外界通过塔釜再沸器输入热量,kJ·h-1;D代表塔顶采出流量,kmol·h-1;ID代表塔顶采出焓,kJ·kmol-1;W代表塔釜采出流量,kmol·h-1;IW代表塔釜液相焓,kJ·kmol-1;QC为由塔顶冷凝器输出热量,kJ·h-1。其中组分1代表乙烷,组分2代表丙烯,组分3代表丙烷,组分4代表异丁烯,组分5代表异丁烷,组分6代表丁烯-1,组分7代表正丁烷,组分8代表反丁烯-1,组分9代表顺丁烯-1。
该案例包含40个连续测量变量和6种工况,涵盖正常工况和5种异常工况(表 1),各种工况的源域和目标域均采集2 000个样本点。为消除不同变量之间量纲的影响,对样本进行了归一化处理。
|
|
表 1 脱丙烷精馏塔工况表 Table 1 Work conditions list of depropanization distillation process |
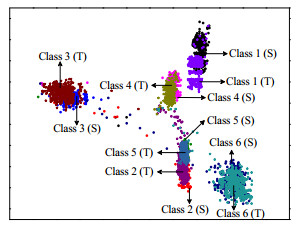
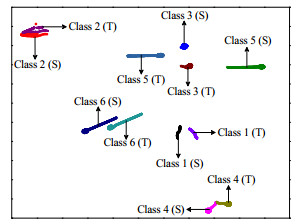
YOSINSKI等[23]证明了神经网络的前3层特征是通用特征,故本文提出的分层卷积特征提取模型采用2层卷积层,其参数如表 2所示。针对化工高维度数据,采用“t-SNE”可视化技术[24]更好地呈现卷积特征提取过程和效果。该技术可以有效映射原始多维特征空间变量至二维空间,从而实现高维数据的可视化[25]。其中原始机理特征分布和第1、2层卷积层特征分布的映射效果如图 3~5所示。由图 3可见,多工况之间相互交错,各工况特征离散度高,工况可分性差。通过第1层卷积层特征提取后(图 4),工况特征的重叠部分大幅度减少,但部分特征的可分性仍然较差。通过第2层卷积层特征提取后(图 5),工况特征的可分性较高,但存在源域(S)和目标域(T)特征分布不一致的情况,容易导致模型识别错误,为此本文适配机理特征分布。
|
图 3 原始机理特征分布可视化图 Fig.3 Visualization map of original mechanism feature distribution |

|
图 4 第1层卷积特征分布可视化图 Fig.4 Visualization map of feature distribution from the first layer convolution |
|
图 5 第2层卷积特征分布可视化图 Fig.5 Visualization map of feature distribution from the second layer convolution |
|
|
表 2 分层卷积特征提取模型参数表 Table 2 Parameters of layered convolution feature extracted model |
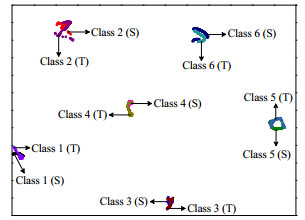
图 6为适配了第2层卷积层的输出特征。可以看出,各工况的源域特征和目标域特征分布情况基本一致,消除了化工过程中特征分布不一致对异常识别的影响。
|
图 6 第2层卷积层机理特征自适应后的特征分布图 Fig.6 Characteristic distribution of mechanism after adaptation from the second layer convolution |
设计的DCNN识别模型参数如表 3所示,采用经验的方法调整模型参数。第1层卷积层采用宽卷积核[26],以有效过滤化工过程产生的噪声。第2、3层采用窄卷积核[27],通过窄卷积核的多层叠加取得了与宽卷积核相同规模的感受野,加深纵向上的网络深度,提高模型识别能力。与相同深度的宽卷积核相比,窄卷积核使用的参数更少。卷积层和池化层均采用高效的ReLU激活函数[28-29]。为识别多工况的化工过程,分类层激活函数采用softmax[30]。DCNN参数学习采用小批量梯度下降中的Adam (adaptive moment estimation)方法,设置批次大小为64,初始化函数设置为he_normal [31]。采用EarlyStopping方法监测网络的损失函数,在损失函数不再下降时,停止迭代训练,以防止识别模型过拟合。
|
|
表 3 异常识别模型参数表 Table 3 DCNN model parameters used in anomaly identification |
为了便于清晰地展示所提方法的性能,定义混合矩阵(表 4)、F1分数(式(9))、故障诊断率(fault diagnosis rate, FDR) (式(10))、误报率(false positive rate, FPR) (式(11))、G-mean指标(式(12))和准确率(式(13))。
|
|
表 4 混合矩阵 Table 4 Confusion matrix |
| $F1 = \rm\frac{{2 \times PRE \times REC}}{{PRE + REC}} \times 100\% $ | (9) |
| $ \rm FDR = \frac{{TP}}{{TP + FN}} \times 100\% $ | (10) |
| $\rm FPR = 1 - \frac{{TN}}{{FP + TN}} \times 100\% $ | (11) |
| $ \rm G - {\rm{mean}} = \sqrt {FDR \times \frac{{TN}}{{FP + TN}}} \times 100\% $ | (12) |
| $ \rm Accuracy = \frac{{TN + TP}}{{FP + TN + TP + FN}} \times 100\% $ | (13) |
将所提出的DMFA-DCNN模型与单一DCNN和深层机理特征(deep mechanism feature, DMF)-DCNN异常工况识别方法对比,应用于脱丙烷精馏过程。其中,DCNN直接识别原始过程数据,DMF-DCNN模型识别经过卷积抽取了工艺机理特征但未经过自适应的特征数据。通过计算F1分数、FPR、FDR、G-mean和准确率指标来比较模型性能,进一步说明DMFA-DCNN模型在工业仿真应用过程中的有效性。脱丙烷精馏塔6种工况的识别结果见表 5~8。在表 5中的6种工况下,DMFA-DCNN相较于DCNN与DMF-DCNN的识别性能整体较优。DMFA-DCNN的平均F1分数为99.87%,相较于DCNN和DMF-DCNN的平均F1分数提高了约2.40%和0.27%。经分析发现DMFA-DCNN的识别效果提升不明显,这是由于DMFA-DCNN识别的精馏异常工况多为阶跃异常,其症状表现明显,异常本身容易被识别,加之DCNN强大的学习能力,故所提出的DMFA-DCNN方法的F1分数提升不明显。
|
|
表 5 DCNN、DMF-DCNN和DMFA-DCNN模型的F1分数 Table 5 F1 scores of DCNN, DMF-DCNN and DMFA-DCNN models |
|
|
表 6 DCNN、DMF-DCNN和DMFA-DCNN模型的FPR Table 6 FPR of DCNN, DMF-DCNN and DMFA-DCNN models |
|
|
表 7 DCNN、DMF-DCNN和DMFA-DCNN模型的FDR Table 7 FDR of DCNN, DMF-DCNN and DMFA-DCNN models |
|
|
表 8 DCNN、DMF-DCNN和DMFA-DCNN模型的G-mean Table 8 G-mean of DCNN, DMF -DCNN and DMFA-DCNN models |
FPR对于工业生产应用有效性具有重要意义,故对FPR进行了对比分析,如表 6所示。DMFA-DCNN的平均FPR仅为0.03%,与DCNN和DMF-DCNN相比降低了93.33%和50.00%。由表 6可见,DCNN模型对于异常2和异常3表现出较高的误报率,分析认为异常2 (再沸器E-702加热蒸汽暂时中断)和异常3 (系统仪表风暂时中断)均为仪表发生异常,导致了脱丙烷精馏过程表现出类似的症状进而区分困难。
表 7显示了DMFA-DCNN模型的FDR结果。由表 7可见,DMFA-DCNN的平均FDR为99.90%,与DCNN和DMF-DCNN相比提高了2.48%和0.27%。
为了全面比较分析模型性能,本文对比了G-mean指标(表 8)。当不同异常工况的训练数据不相同时,G-mean指标具有较大参考价值。G-mean指标是与F1分数不同的另一种评价模型性能的指标,被定义为准确率和故障诊断率的几何平均数。由表 8可见,DMFA-DCNN平均G-mean为99.93%,与DCNN和DMF-DCNN相比提高了1.47%和0.18%。
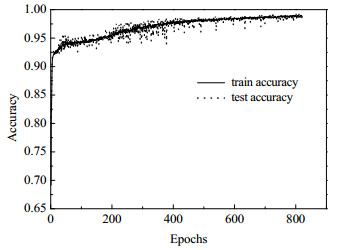
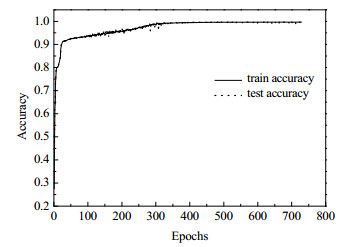
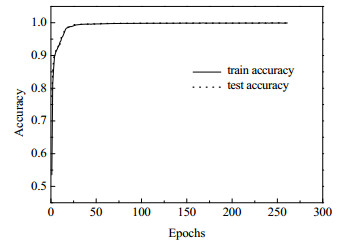
图 7~9显示了DCNN、DMF-DCNN和DMFA-DCNN模型的准确率。由图 9可见,DMFA-DCNN在迭代261次时到达停止训练条件,相较DCNN (图 7)和DMF-DCNN (图 8)识别模型具有更高的识别精度和收敛速度。同时由表 9的运行时间对比结果可见,DMFA-DCNN运行时间仅为10.56 s (在Core i5, 8 GB内存电脑上测试),与DCNN和DMF-DCNN相比节省了72.25%和67.11%的运行时间。
|
图 7 DCNN对于6种工况的识别准确率 Fig.7 Identification accuracy of DCNN model for six conditions |
|
图 8 DMF-DCNN对于6种工况的识别准确率 Fig.8 Identification accuracy of DMF-DCNN model for six conditions |
|
图 9 DMFA-DCNN对于6种工况的识别准确率 Fig.9 Identification accuracy of DMFA-DCNN model for six conditions |
|
|
表 9 DCNN, DMF-DCNN和D MFA-DCNN模型的运行时间 Table 9 Running time of DCNN, DMF-DCNN and DMFA-DCNN models |
为充分证明本文所提出方法的有效性,还与LI等[10]提出的CNN-DAE方法进行了对比,结果如表 10所示。可见,DMFA-DCNN相较CNN-DAE识别模型的平均准确率提升了8.37%。
|
|
表 10 CNN-DAE和DMFA-DCNN模型的准确率 Table 10 Accuracy of CNN-DAE and DMFA-DCNN models |
本文提出了一种基于多工况深层机理特征自适应的异常识别方法DMFA-DCNN。F1分数、FPR、FDR、G-mean和准确率指标分析结果表明,DMFA-DCNN识别模型平均F1分数达到99.87%,平均FPR为0.03%,平均FDR达到99.90%,运行时间仅为10.56 s,较DCNN和DMF-DCNN识别模型具有更低的误报率、更高的故障诊断率和更短的运行时间。该方法对于异常前期的识别精度仍然较低,如何及时有效地识别微小异常将是以后研究的重点。
| [1] |
梁慧婷, 田文德, 靳满满, 等. 精馏过程单变量扰动原因的智能反演[J]. 高校化学工程学报, 2016, 30(6): 1300-1305. LIANG H T, TIAN W D, JIN M M, et al. Intelligent inversion of single variable disturbance in distillation processes[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(6): 1300-1305. |
| [2] |
郭金玉, 王鑫, 李元. 基于加权差分主元分析的化工过程故障检测[J]. 高校化学工程学报, 2018, 32(1): 183-192. GUO J Y, WANG X, LI Y. Fault detection in chemical processes using weighted differential principal component analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(1): 183-192. |
| [3] |
张汉元, 田学民. 基于异步PCA的故障识别方法[J]. 高校化学工程学报, 2016, 30(3): 680-685. ZHANG H Y, TIAN X M. A fault identification method based on asynchronous PCA[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(3): 680-685. |
| [4] |
郭小萍, 徐月, 李元. 基于特征空间自适应k近邻工业过程故障检测[J]. 高校化学工程学报, 2019, 33(2): 453-461. GUO X P, XU Y, LI Y. A feature space adaptive k-nearest neighbor method for industrial fault detection[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(2): 453-461. |
| [5] |
耿志强, 徐猛, 朱群雄, 等. 基于深度学习的复杂化工过程软测量模型研究与应用[J]. 化工学报, 2019, 70(2): 564-571. GENG Z Q, XU M, ZHU Q X, et al. Research and application of soft measurement model for complex chemical processes based on deep learning[J]. CIESC Journal, 2019, 70(2): 564-571. |
| [6] |
HOANG D T, KANG H J. A survey on deep learning based bearing fault diagnosis[J]. Neurocomputing, 2019, 335: 327-335. DOI:10.1016/j.neucom.2018.06.078 |
| [7] |
LEI J H, LIU C, JIANG D X. Fault diagnosis of wind turbine based on long short-term memory networks[J]. Renewable Energy, 2019, 133: 422-432. DOI:10.1016/j.renene.2018.10.031 |
| [8] |
HUA F, FANG Z, QIU T. Application of convolutional neural networks to large-scale naphtha pyrolysis kinetic modeling[J]. Chinese Journal of Chemical Engineering, 2018, 26(12): 2562-2572. DOI:10.1016/j.cjche.2018.09.021 |
| [9] |
WU H, ZHAO J S. Deep convolutional neural network model based chemical process fault diagnosis[J]. Computers & Chemical Engineering, 2018, 115: 185-197. |
| [10] |
LI C K, ZH D F, MU S J, et al. Fault diagnosis for distillation process based on CNN-DAE[J]. Chinese Journal of Chemical Engineering, 2019, 27(3): 598-604. DOI:10.1016/j.cjche.2018.12.021 |
| [11] |
CHEN C, JIANG B Y, CHENG Z W, et al. Joint domain matching and classification for cross-domain adaptation via ELM[J]. Neurocomputing, 2019, 349: 314-325. DOI:10.1016/j.neucom.2019.01.056 |
| [12] |
PAN S J, YANG Q. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345-1359. DOI:10.1109/TKDE.2009.191 |
| [13] |
SAITO K, USHIKU Y, HARADA T. Asymmetric tri-training for unsupervised domain adaptation[C]// Proceedings of the 34th International Conference on Machine Learning, Piscataway: JMLR, 2017: 2988-2997.
|
| [14] |
LONG M S, WANG J M, DING G G, et al. Transfer feature learning with joint distribution adaptation[C]// 2013 IEEE International Conference on Computer Vision, Piscataway: IEEE, 2013: 2200-2207.
|
| [15] |
LI X, ZHANG W, DING Q, et al. Multi-layer domain adaptation method for rolling bearing fault diagnosis[J]. Signal Processing, 2019, 157: 180-197. DOI:10.1016/j.sigpro.2018.12.005 |
| [16] |
WANG J D, CHEN Y Q, HAO S J, et al. Balanced distribution adaptation for transfer learning[C]// 2017 IEEE International Conference on Data Mining, Piscataway: IEEE, 2017: 1129-1134.
|
| [17] |
TAHMORESNEZHAD J, HASHEMI S. Visual domain adaptation via transfer feature learning[J]. Knowledge & Information Systems, 2016, 50(2): 585-605. |
| [18] |
HSIAO P H, CHANG F J, Lin Y Y. Learning discriminatively reconstructed source data for object recognition with few examples[J]. IEEE Transactions on Image Processing, 2016, 25(8): 3518-3532. DOI:10.1109/TIP.2016.2572602 |
| [19] |
ZHANG J, LI W Q, OGUNBONA P. Joint geometrical and statistical alignment for visual domain adaptation[C]// 2017 IEEE Conference on Computer Vision and Pattern Recognition, Piscataway: IEEE, 2017: 5150-5158.
|
| [20] |
WANG X G, JIE R, LIU S. Distribution adaptation and manifold alignment for complex processes fault diagnosis[J]. Knowledge-Based Systems, 2018, 156: 100-112. DOI:10.1016/j.knosys.2018.05.023 |
| [21] |
龙明盛.迁移学习问题与方法研究[D].北京: 清华大学, 2014. LONG M S. Transfer learning: problems and methods[D]. Beijing: Tsinghua University, 2014. |
| [22] |
李传坤, 赵东风, 王春利, 等. 一种化工过程故障诊断知识自动化方法研究[J]. 高校化学工程学报, 2018, 32(2): 393-400. LI C K, ZHAO D F, WANG C L, et al. Study on a knowledge automation method for fault diagnosis of chemical processes[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(2): 393-400. |
| [23] |
YOSINSKI J, CLUNE J, BENGIO Y, et al. How transferable are features in deep neural networks?[C]// Proceedings of the 27th International Conference on Neural Information Processing Systems, Piscataway: NIPS, 2014: 3320-3328.
|
| [24] |
MAATEN L, HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9: 2579-2605. |
| [25] |
ROMAN-RANGEL E, MARCHAND-MAILLET S. Inductive t-SNE via deep learning to visualize multi-label images[J]. Engineering Applications of Artificial Intelligence, 2019, 81: 336-345. DOI:10.1016/j.engappai.2019.01.015 |
| [26] |
张伟.基于卷积神经网络的轴承故障诊断算法研究[D].哈尔滨: 哈尔滨工业大学, 2017. ZHANG W. Study on bearing fault diagnosis algorithm based on convolutional neural network[D]. Harbin: Harbin Institute of Technology, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10213-1017864225.htm |
| [27] |
ZHANG W, LI C H, PENG G L, et al. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load[J]. Mechanical Systems and Signal Processing, 2018, 100: 439-453. DOI:10.1016/j.ymssp.2017.06.022 |
| [28] |
ECKLE K, SCHMIDT-HIEBER J. A comparison of deep networks with ReLU activation function and linear spline-type methods[J]. Neural Networks, 2019, 110: 232-242. DOI:10.1016/j.neunet.2018.11.005 |
| [29] |
NAIR V, E. HINTON G. Rectified linear units improve restricted boltzmann machines[C]// Proceedings of the 27th international conference on machine learning, Piscataway: ICML, 2010: 807-814.
|
| [30] |
ADEM K, KILICARSLAN S, COMERT O. Classification and diagnosis of cervical cancer with stacked autoencoder and softmax classification[J]. Expert Systems with Applications, 2019, 115: 557-564. DOI:10.1016/j.eswa.2018.08.050 |
| [31] |
HE K, ZHANG X Y, REN S Q, et al. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[C]// 2015 IEEE International Conference on Computer Vision, Piscataway: IEEE, 2015: 1026-1034.
|




