气固并流下行床是当代流态化技术中相对活跃的研究领域之一,与传统的气固并流上行提升管相比具有诸多优势[1-2]。颗粒浓度沿径向的分布是下行床气固两相流动特性的重要参数,许多研究者对此进行了研究[3-6]。
与下行床类似,气固并流上行循环流化床提升管内颗粒浓度存在更为显著的径向分布不均现象。但是对于这种不均匀结构的成因,大多研究只是定性描述现象[7],即使尝试进行理论解释[8],也并未给出有说服力的定量分析。本文认为,无论是下行床还是提升管,其内颗粒浓度径向不均匀分布显然与颗粒(群)受到的沿径向的某个横向作用力(或合力)有关——正是该作用力(或合力)的存在,“阻止”了浓度梯度的扩散。因此,有必要从颗粒(群)受力出发,为下行床径向分布不均匀结构的成因提出更充分的解释。
李晨[9]在研究中计算得到固体颗粒所受到几个力的数量级,因此本文认为:下行床内颗粒所受到的与流动方向垂直的横向力主要有热泳力、贝赛特力、马格努斯力和萨夫曼力。周涛等[10]发现温度梯度较大时,颗粒会在热泳力作用下发生热泳沉积。而冷模实验中温度梯度基本为零,但是颗粒浓度的径向分布依然不均匀。因此,可以断定热泳力不是导致颗粒浓度径向分布不均匀的主要原因。贝赛特力与固体和流体之间的相对加速度有关[11],而颗粒的实际加减速方向往往很难预测,因此贝赛特力也不是颗粒浓度径向分布不均匀的主要原因。黄社华等[12]的研究表明萨夫曼力在主流区域的作用很小一般可以忽略,而只在边界层区域内加以考虑。因此在本文中,萨夫曼力不适用于分析整个床层的颗粒受力情况。
马格努斯力与颗粒旋转有关[13],有实验研究[14]证明床内颗粒是高速旋转的,数值模拟[15-16]也发现当考虑颗粒旋转作用后,床内更容易形成非均匀流动结构。但很难想象在下行床中某一个区域内所有颗粒都朝一个方向旋转,因此马格努斯力不应是颗粒浓度径向分布不均匀的主要原因。
FAN等[13]、李晨等[17]从颗粒群受力的角度分析了提升管内颗粒浓度的径向分布;但对于径向浓度分布更加复杂的下行床——几乎没有相关研究讨论其成因。本文将空气动力学的理论和场论“移植”到两相流中,引入Kutta-Joukowski横向力解释、量化下行床内颗粒浓度径向不均匀分布形成的原因。通过分析他人实验数据中所给出的下行床内颗粒的速度、浓度径向分布,确定了不同操作条件下,Kutta-Joukowski力对颗粒浓度径向分布的影响。
2 理论分析根据空气动力学[18],气固两相流场中Kutta-Joukowski力可以表示为
| ${F_{{\rm K - J}}} = {\rho _{\rm{g}}}\left( {{\nu _{{\rm p, z}}} - {\nu _{{\rm g, z}}}} \right)\varGamma $ | (1) |
式中:
根据斯托克斯定理[18],在任一由封闭曲线包围的单连通区域内,如果流体的密度为常数,沿曲线的速度环量Г等于这个区域内的涡强度I,即
| $\varGamma {\rm{ = }}I$ | (2) |
而涡强度和速度旋度的关系为
| $I{\rm{ = 2}}A\varOmega $ | (3) |
对于下行床的正交坐标系而言,取其Z轴正方向向下,故速度旋度Ω、涡强度I和速度环量Г沿顺时针方向为正,逆时针方向为负。
另一方面,速度旋度是速度梯度的函数,可由式(4)计算:
| $\varOmega = \frac{1}{2}\left( {\frac{{\partial {\nu _{{\rm p, r}}}}}{{\partial {\rm z}}} - \frac{{\partial {\nu _{p, z}}}}{{\partial r}}} \right)$ | (4) |
式中
对于任意微小封闭单连域内的颗粒群,Kutta-Joukowski力产生的2个要素同时存在,即
| $ F_{\mathrm{K}-\mathrm{J}}=\rho_{\mathrm{g}}\left(v_{\mathrm{p}, \mathrm{z}}-v_{\mathrm{g}, \mathrm{z}}\right) \Gamma=\rho_{\mathrm{g}}\left(v_{\mathrm{p}, \mathrm{z}}-v_{\mathrm{g}, \mathrm{z}}\right)\left(\frac{\partial v_{\mathrm{p}, \mathrm{r}}}{\partial z}-\frac{\partial v_{\mathrm{p}, {\rm z}}}{\partial r}\right) A $ | (5) |
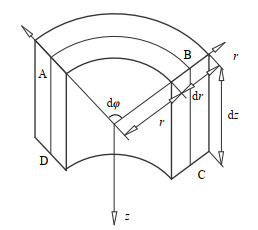
下行床的形状多为圆柱体,因此本文取柱坐标系的一个微元体如图 1所示。
|
图 1 下行床内极坐标微元体 Fig.1 Scheme of micro-unit in polar coordinate |
Kutta-Joukowski横向力的作用位置为微元体中间截面ABCD,作用对象为微元体空间内所包含的颗粒群;颗粒群受到的Kutta-Joukowski横向力为
| $ \mathrm{d} F_{\mathrm{K}-\mathrm{J}}=\rho_{\mathrm{g}}\left(v_{\mathrm{p}, \mathrm{z}}-v_{\mathrm{g}, \mathrm{z}}\right)\left(-\frac{\partial v_{\mathrm{p}, z}}{\partial r}\right)\left(r+\frac{\mathrm{d} r}{z}\right) \mathrm{d} r \mathrm{d} z \mathrm{d} \theta $ | (6) |
单连通域所包含颗粒群受到的单位面积Kutta-Joukowski横向力为
| $ F_{\mathrm{K}-\mathrm{J}}=-\rho_{\mathrm{g}}\left(v_{\mathrm{p}, \mathrm{z}}-v_{\mathrm{g}, \mathrm{z}}\right)\left(\frac{\partial v_{\mathrm{p}, z}}{\partial r}\right) r $ | (7) |
值得注意的是,在上述推导过程中,因为下行床内大多数区域的颗粒径向速度远小于轴向速度,因此引入了
为了获得Kutta-Joukowski横向力的数值,需要确定速度矢量差
本文式(7)中速度梯度是基于ZHANG等[19]和WANG等[5]发表的实验数据,通过读取局部颗粒速度的数值,得到速度梯度的数值。
式(7)中
| $ \frac{u_{\mathrm{s}}}{u_{\mathrm{t}}}=D^{8 / 7}\left(1-\varepsilon_{\mathrm{mf}}\right)^{-2 / 7}\left[\frac{1-\varepsilon}{\varepsilon}\right]^{8 / 7} \varepsilon^{47 / 14} \frac{\varepsilon-\varepsilon_{\mathrm{mf}}}{\varepsilon} $ | (8) |
式中:
第2种方法则是曹春社等[21]通过同时测定气相和固相的局部速度获得的,即
| $ u_{\mathrm{s}}=5.478(1-\varepsilon)^{0.539}\left({Re} / {Re}_{\mathrm{t}}\right)^{0.042} $ | (9) |
式中:
通过试算,发现由式(8)计算得到的局部滑落速度远小于颗粒终端速度;而采用式(9)获得的数值与实验数据吻合较好,因此本文采用式(9)来确定式(7)中的局部滑落速度。
下行床内Kutta-Joukowski横向力的方向与速度矢量差(即滑落速度的方向)有关,因此在通过式(7)计算Kutta-Joukowski横向力时,得到的计算结果并不能准确的表示Kutta-Joukowski横向力的方向,还需要进行具体分析。
3 气体速度径向分布特征速度矢量差(即滑落速度的方向)决定了Kutta-Joukowski横向力的方向,应分析下行床内局部气速、颗粒速度的相对大小关系。
根据WANG等[3, 5-6]的实验结果——颗粒于边壁大量聚集而中心区浓度较低,分析可知:由于颗粒大量聚集于边壁,限制了气体在边壁区域的流动——大部分气体流经除边壁的中间区域,因此中心r/R = 0~0.316区域的气速比较高,颗粒速度始终小于局部气速;而在r/R ≈ 0.8~0.95的边壁高浓度区,由于颗粒大量聚集,颗粒之间相互碰撞同样会使颗粒动能大量耗散,同时床内颗粒会“裹挟”气体下行,对气体有“助力”作用,因此颗粒速度小于局部气速。而对于r/R ≈ 0.316~0.8区域内气体速度与颗粒速度之间的关系则需要进一步分析。
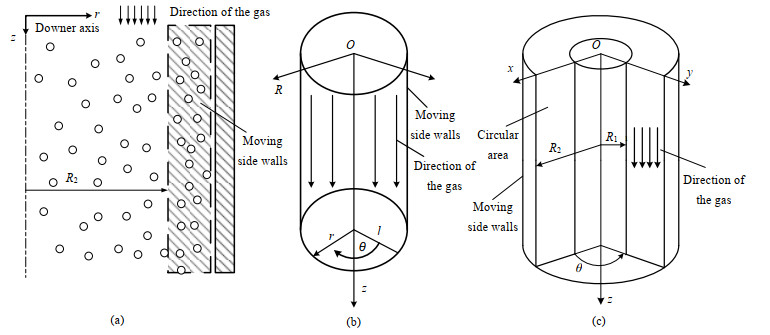
曹春社等[21]的研究表明:沿下行床径向,气体速度从中心逐渐增加并在r/R ≈ 0.86~0.96达到极大值然后减小(事实上,曹春社等[21]、杨勇林等[22]实验中,颗粒速度的极大值也出现在r/R ≈ 0.86~0.96区域内),但却从未有人对下行床中这个气相速度分布的形成原因进行分析。显然,这个分布在对称管流中非常“罕见”,管流速度最高点没有出现在管中心。本文认为,这正是由于边壁大量颗粒下滑“带动气体”向下运动造成的,边壁区域大量下行的颗粒相当于“构造”了一个“运动的边壁”,从而改变了速度分布,使气相速度最高点的位置向边壁移动,如图 2(a)所示。具体理论分析采用单相流体力学“比拟”,认为下行气体对气相流场的影响相当于是形成了一个以速度Vw向下移动的边壁。以WANG等[3, 5-6]的实验为例分析了下行床内局部气速的分布特征。
|
图 2 柱坐标中流体的定常流动 Fig.2 Steady flow of fluid in cylindrical coordinate |
假设气体在下行床中做定常流动,对一般流体而言——流体密度为常量而且温度变化范围不大,在不可压缩条件下状态方程消失,连续方程和动量方程[23]可写为
| $ \begin{array}{l} \nabla \cdot V=0 \\ \frac{\mathrm{d} V}{\mathrm{d} t}=F-\frac{1}{\rho} \nabla p+υ \nabla V \end{array} $ | (10) |
在如图 2(b)所示柱坐标系中,虑到定常条件∂u/∂t=0以及连续性,方程可简化为
| $ \frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial u}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} u}{\partial \theta^{2}}=\frac{1}{\mu} \frac{\partial p}{\partial x} $ | (11) |
考虑到轴对称性——即u=u(r), 对方程关于r积分两次得
| $ u=\frac{1}{\mu} \frac{\partial p}{\partial x} \frac{r^{2}}{4}+C_{1} \ln r+C_{2} $ | (12) |
如图 2(c)所示,边界条件取在r = R2(R2 > 0.8)——即“运动的边壁”,以及r = R1(0 < R1 < 0.316)——床层中心区域(之所以不取r = 0,是因为在该边界条件下积分常数C1恒为零,失去意义)。床层中心区域的气速不为零,因此在r = R1处u ≠ 0;而由于“运动的边壁”的存在,在r = R2处同样有u ≠ 0。所以,边界条件为
| $ \begin{array}{l} r=R_{1} \quad \text { 时 }, \quad u=V_{\mathrm{c}} \\ r=R_{2} \quad \text { 时 }, \quad u=V_{\mathrm{w}} \end{array} $ | (13) |
代入边界条件得
| $ \begin{array}{l} \frac{1}{\mu} \frac{\partial P}{\partial x} \frac{R_{1}^{2}}{4}+C_{1} \ln R_{1}+C_{2}=V_{\mathrm{c}} \\ \frac{1}{\mu} \frac{\partial P}{\partial x} \frac{R_{2}^{2}}{4}+C_{1} \ln R_{2}+C_{2}=V_{\mathrm{w}} \end{array} $ | (14) |
于是求得积分常数为
| $ \begin{array}{c} C_{1}=\frac{\left(V_{\mathrm{w}}-V_{\mathrm{c}}\right)-\left(\frac{1}{\mu} \frac{\partial P}{\partial x} \frac{R_{2}^{2}}{4}-\frac{1}{\mu} \frac{\partial P}{\partial x} \frac{R_{1}^{2}}{4}\right)}{\ln R_{2}-\ln R_{1}} \\ C_{2}=\frac{V_{\mathrm{w}} \ln R_{2}-V_{\mathrm{c}} \ln R_{1}+\frac{1}{\mu} \frac{\partial P}{\partial x}\left(\frac{R_{2}^{2}}{4} \ln R_{1}-\frac{R_{1}^{2}}{4} \ln R_{2}\right)}{\ln R_{2}-\ln R_{1}} \end{array} $ |
则该空间内的速度分布为
| $ u=\frac{1}{\mu} \frac{\partial P}{\partial x} \frac{r^{2}}{4}+\frac{\left(V_{\mathrm{w}}-V_{\mathrm{c}}\right)-\frac{1}{\mu} \frac{\partial p}{\partial x}\left(\frac{R_{2}^{2}}{4}-\frac{R_{1}^{2}}{4}\right)}{\ln R_{2}-\ln R_{1}} \ln r+\frac{V_{\mathrm{c}} \ln R_{2}-V_{\mathrm{w}} \ln R_{1}+\frac{1}{\mu} \frac{\partial P}{\partial x}\left(\frac{R_{2}^{2}}{4} \ln R_{1}-\frac{R_{1}^{2}}{4} \ln R_{2}\right)}{\ln R_{2}-\ln R_{1}} $ | (15) |
相应的速度极值出现在r0处:
| $ r_{0}=\left[2 \frac{\left(V_{\mathrm{w}}-V_{\mathrm{c}}\right)-\left(\frac{1}{\mu} \frac{\partial P}{\partial x} \frac{R_{2}^{2}}{4}-\frac{1}{\mu} \frac{\partial P}{\partial x} \frac{R_{1}^{2}}{4}\right)}{\frac{1}{\mu} \frac{\partial P}{\partial x}\left(\ln R_{2}-\ln R_{1}\right)}\right]^{\frac{1}{2}} $ | (16) |
显然气体速度的极值点r0存在而且与Vc和Vw的具体数值有关;由式(16)可知,在r/R ≈ R1-R2的区域气体速度存在极值点。这也印证了曹春社等[21]的实验结果,因此认为在r = r0处为速度极大值点;该点并不像通常单相对称管流一样,位于r/R = 0及r/R = 1处。若Vw增加,这个极值速度所处的位置r0向边壁移动;若Vc增加,r0向床中心移动。根据上述单相管流的“比拟”分析可知,对于气固下行床,当操作条件改变时,边壁高浓度区的颗粒浓度、速度也会改变,从而影响边界条件所取Vw值改变,导致速度极值点r0发生变化。
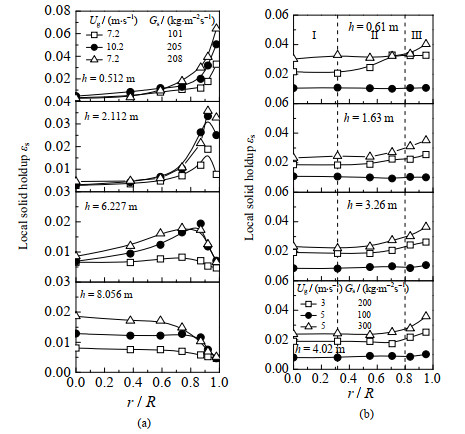
4 Kutta-Joukowski横向力对颗粒径向分布的“贡献” 4.1 颗粒浓度径向分布的两种形式ZHANG等[4]实验中下行床颗粒浓度径向分布如图 3(a)所示。沿下行床径向,上部浓相区是典型的“环-核结构”,同一截面的中心区域颗粒浓度低,边壁环形区颗粒浓度高。随着气固并流下行,颗粒浓度的局部最大值从边壁向中心“移动”,最终形成呈中心浓、边壁稀的“反环-核分布”。WANG等[5]通过实验测得的颗粒浓度分布如图 3(b),循环量为100 kg·m-2·s-1时,颗粒浓度在r/R ≈ 0~0.8区域分布比较均匀,仅在近壁区(r/R > 0.8)有所增加;在较高循环量下,颗粒浓度沿径向增加并在边壁达到最大值,与提升管中颗粒浓度的分布相似——“环-核结构”(虽然浓度梯度明显小于提升管)。针对这2种明显不同径向分布“形态”,需根据颗粒质量流率、入口气速-压力等具体条件分析Kutta-Joukowski横向力。
|
图 3 下行床颗粒浓度径向分布 Fig.3 Radial distribution of particle solid holdup in a downer |
本文根据公开发表的ZHANG等[4, 19]和WANG等[3, 5-6]的实验数据,通过分析式(7)中的速度矢量差及速度梯度数值的正负,分析Kutta-Joukowski力对下行床颗粒浓度径向分布的“贡献”。
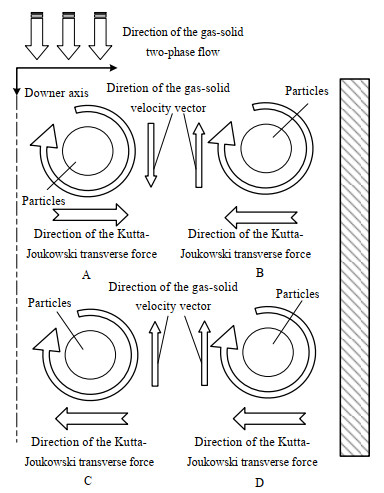
4.2 Kutta-Joukowski力对下行床颗粒浓度径向分布的“贡献”下行床内不同区域颗粒(群)所受Kutta-Joukowski力如图 4所示。由上述分析可知,下行床颗粒(群)受到的Kutta-Joukowski力的方向为νg-νp矢量方向沿速度环量方向的反方向旋转90°。根据读取的ZHANG等[19]实验中颗粒速度数据,不同截面内沿径向有∂νp, z/∂r < 0,即速度旋度Ω > 0,Γ > 0。
|
图 4 Kutta−Joukowski力对下行床内颗粒群的作用 Fig.4 Effects of Kutta−Joukowski force on particles in the downer |
与提升管不同,下行床内颗粒逐渐加速,最终甚至超过局部气速,因此式(7)中νp, z-νg, z的方向沿轴向将发生变化,须分区进行讨论。如图 3、4所示,在颗粒加速段的中心区(A区域),由于颗粒刚开始加速,颗粒速度小于气速,即νg-νp的方向竖直向下,而速度环量为顺时针,因此颗粒群受到的Kutta-Joukowski横向力指向下行床壁面。在颗粒加速段边壁区(B区域),颗粒轴向速度较小,而气体速度则由于边壁的存在其数值为0,因此颗粒群受到的Kutta-Joukowski横向力指向中心。在充分发展段的中心区(C区域),此时颗粒已经完成轴向加速过程,其轴向速度大于气体速度,因此颗粒受到的Kutta-Joukowski横向力指向床中心。在充分发展段的边壁区(D区域),气体速度由于边壁限制趋近于0,其内颗粒所受Kutta-Joukowski横向力也指向床中心。
综合图 3、4可知Kutta-Joukowski横向力对颗粒浓度径向分布的影响过程:颗粒在入口处大量聚集于近壁区,颗粒浓度在该处达到最大值。在颗粒加速段,由于A、B区域中Kutta-Joukowski横向力方向相反,在该力的“驱动下”,大量颗粒聚集在介于边壁和床中心的区域,因而该处出现了颗粒浓度的最大值,而后由于颗粒的加速运动——到了充分发展段,C、D区域内颗粒所受Kutta-Joukowski横向力均指向中心,使得颗粒浓度的最大值由从边壁转移到中心。
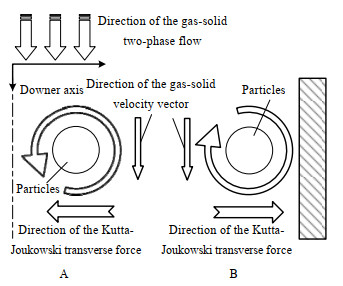
而在WANG等[3, 5-6]的实验中,颗粒速度沿径向逐渐增加,在r/R ≈ 0.8处达到最大值然后减小。在床层中心r/R = 0~0.316区域内存在颗粒浓度的局部极小值——显然床层中心存在颗粒浓度降低的区域,如图 3(I区域)。该区域内颗粒速度沿径向逐渐增加,有∂νp, z/∂r > 0,速度旋度Ω < 0,Γ < 0;而且颗粒速度始终小于局部气速。如图 5(A区域)所示,νg-νp的方向竖直向下,速度环量为逆时针,因此该区域Kutta-Joukowski力方向为νg-νp的方向顺时针旋转90°,指向下行床中心。而在r/R ≈ 0.8~0.95的高浓度区——图 3(Ⅲ区域),由于颗粒速度有减小的趋势,因此有:∂νp, z/∂r < 0,速度旋度Ω > 0,Γ > 0。该区域内颗粒速度小于局部气速,因此νg-νp的方向竖直向下,速度环量为顺时针,颗粒(群)受到的Kutta-Joukowski力方向为νg-νp的方向逆时针旋转90°,指向下行床边壁,在边壁形成高浓度区,如图 5(B区域)所示。
|
图 5 Kutta−Joukowski力对下行床内颗粒群的作用 Fig.5 Effects of Kutta−Joukowski force on particles in the downer |
根据上节内容,气体速度在r/R ≈ R1-R2区域内先增加后减小,而且在边界r = R1、r = R2处气体速度均大于颗粒速度,因此可以判断在r/R ≈ R1-R2整个区域内气体速度大于颗粒速度,同理r/R ≈ 0.316~0.8区域内气体速度大于颗粒速度。在r/R ≈ 0.316~0.8区域内颗粒速度沿径向增加,因此有∂νp, z/∂r > 0,速度旋度Ω < 0,Γ < 0。同时局部气速始终大于颗粒速度——νg-νp的方向竖直向下,速度环量为逆时针,因此该区域内Kutta-Joukowski力指向中心,如图 5(A区域)所示。
但是,r/R ≈ 0.316~0.8区域内颗粒浓度沿径向接近均匀分布(Gs=100 kg·m-2·s-1)或者沿径向缓慢增加(Gs > 100 kg·m-2·s-1),而Kutta-Joukowski力的方向却指向床层中心,很明显是矛盾的。之所以出现这种结果,本文认为是因为该区域内颗粒浓度较低,而且Kutta-Joukowski力也非常小——约为r/R ≈ 0.8~0.95区域Kutta-Joukowski力的1/10,因此对颗粒径向分布的作用不明显。
综上所述,可知颗粒浓度沿径向的不均匀分布主要受Kutta-Joukowski横向力的影响,Kutta-Joukowski横向力是导致局部颗粒浓度径向分布的主要原因。
5 结果与讨论 5.1 颗粒群所受Kutta-Joukowski力和“浓度梯度力”FAN等[13]针对气固并流上行提升管的研究表明:Kutta-Joukowski横向力和固含率沿提升管径向的分布具有极其相似的“形态”。由此可以判断,沿径向方向,提升管内的颗粒群一定受到某个指向提升管中心的力(即由浓度高处指向浓度低处),与Kutta-Joukowski横向力相平衡,使得提升管内颗粒浓度的径向分布保持相对稳定。即颗粒浓度会产生一个浓度“势”,在靠近边壁的环形区域颗粒浓度高,其浓度“势”较大,在中心区域颗粒浓度相对较低,其浓度“势”较小。
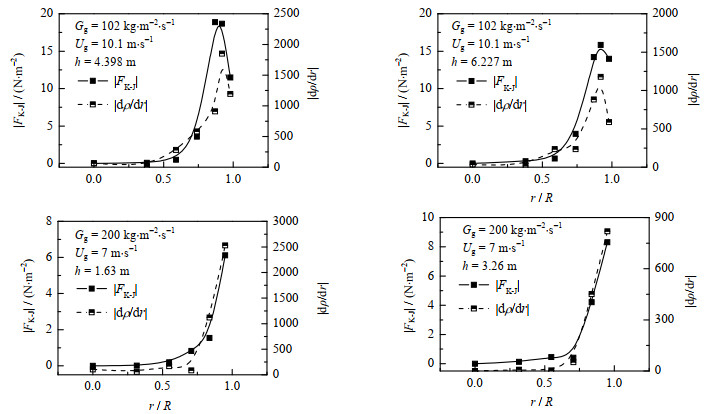
与此类似,本文按照式(7)中Kutta-Joukowski横向力的计算方法,结合ZHANG等[4, 19]和WANG等[3, 5-6]的实验数据,计算了所有径向位置的Kutta-Joukowski横向力。对比发现,Kutta-Joukowski横向力的绝对值与浓度梯度的绝对值沿下行床径向的分布具有极其相似的“形态”——甚至二者“拐点”的位置也几乎一致,如图 6所示。在r/R = 0~0.7区域,Kutta-Joukowski横向力和浓度梯度较小。在r/R > 0.7区域,Kutta-Joukowski横向力和浓度梯度较大且沿径向快速增加。
|
图 6 Kutta-Joukowski横向力和颗粒浓度梯度的径向分布 Fig.6 Radical distributions of Kutta-Joukowski force and solid concentration gradient |
鉴于这种径向分布是稳定存在的,则沿下行床径向方向,颗粒群一定受到某个力(即由浓度高处指向浓度低处)与Kutta-Joukowski横向力相平衡,使得下行床内颗粒浓度的径向分布保持相对稳定。事实上,对于类似的气固并流上行提升管中两相流动体系,即存在一个“浓度梯度力”与提升管内颗粒群受到的Kutta-Joukowski横向力相平衡[13]。
浓度梯度dρ/dr与颗粒径向分布有关,虽然不是矢量,但是有正、负之分。上述浓度梯度力Fρ方向为:浓度高处指向浓度低处。结合dρ/dr的正负差异,可以看出:当dρ/dr为正值时,Fρ指向下行床中心;当dρ/dr为负值时,Fρ指向下行床边壁。因此,可以认为每个径向位置dρ/dr的值决定了该位置Fρ的方向。
下行床中浓度梯度力定义为
| $ F_{\rm{ \mathsf{ ρ}}}=K \frac{\mathrm{d} \rho}{\mathrm{d} r} A $ | (17) |
式中:K为浓度梯度力系数,单位是m3·s-2;ρ为颗粒的局部密度,可由颗粒密度与局部固含率计算;A为“浓度势”作用区域面积沿垂直于力作用方向的投影。
浓度梯度力Fρ与Kutta-Joukowski横向力的方向是相反的,因此每个径向位置dρ/dr的正负与Kutta-Joukowski力的方向呈对应关系。因此本文认为,浓度梯度dρ/dr与Kutta-Joukowski横向力呈显著的对应关系。dρ/dr的正负与Kutta-Joukowski力的方向的对应关系很明显是确定的,为了表征浓度梯度dρ/dr与Kutta-Joukowski横向力在数值上的对应关系,本文均采用绝对值进行分析。
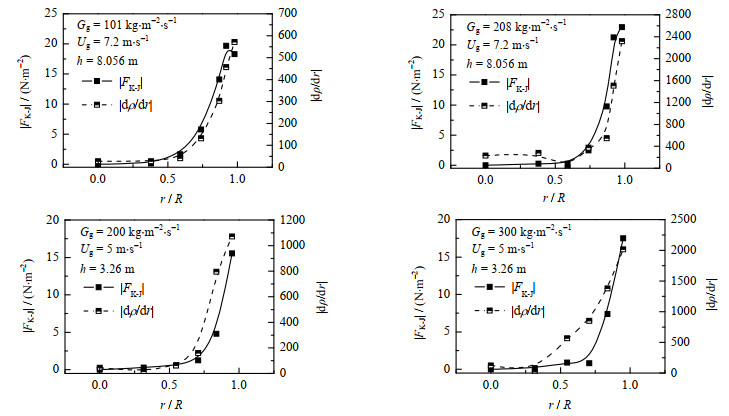
5.2 颗粒循环量对Kutta-Joukowski力的影响图 7为Kutta-Joukowski横向力随颗粒循环量的变化。结果表明,Kutta-Joukowski横向力随颗粒循环量增大而增大,而且近壁区Kutta-Joukowski横向力增加的幅度大于中心区域。这是因为随着颗粒循环强度增加,各径向位置的局部颗粒浓度增大,颗粒之间的动量交换增强,导致颗粒速度径向不均匀程度增加——即颗粒速度梯度增加,从而使Kutta-Joukowski横向力增大。而且,大量颗粒聚集于近壁区,导致近壁区颗粒之间动量交换强于中心区颗粒,从而使近壁区Kutta-Joukowski横向力增加的幅度大于中心区域。
|
图 7 Kutta-Joukowski横向力和颗粒浓度梯度的径向分布 Fig.7 Radical distributions of Kutta-Joukowski force and solid concentration gradient |
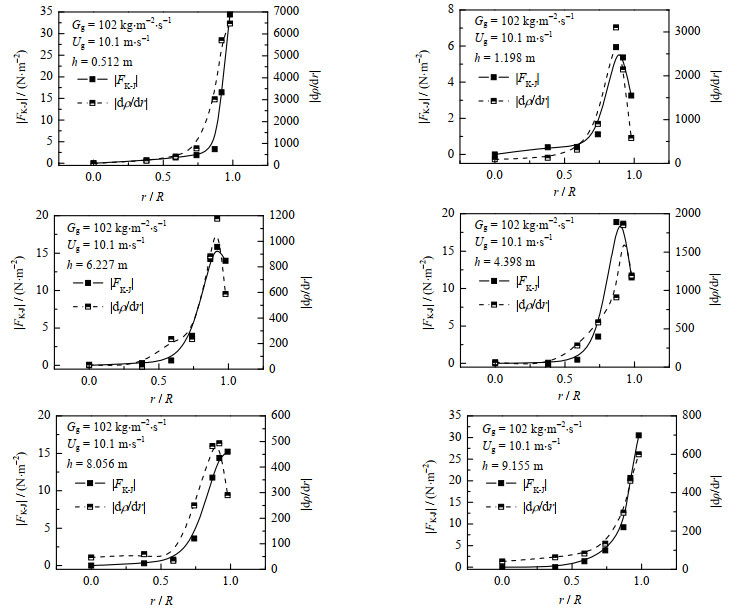
不同轴向位置Kutta-Joukowski横向力的径向分布如图 8所示。结果表明,Kutta-Joukowski横向力随轴向位置增高先减小再增加,并逐渐趋于稳定。
|
图 8 颗粒循环量Gs=102 kg·m-2·s-1、表观气速Ug=10.1 m·s-1时不同轴向位置Kutta−Joukowski力的分布 Fig.8 Radial profiles of Kutta−Joukowski force at different axial heights with Gs=102 kg·m-2·s-1 and Ug=10.1 m·s-1 |
气固并流下行床内颗粒会经历第1加速段、第2加速段及充分发展段[1]。根据式(7)中Kutta-Joukowski横向力的计算方法,可知其大小与颗粒速度梯度及滑落速度有关。沿下行床轴向,滑落速度的变化很小,因此Kutta-Joukowski横向力的大小主要受颗粒速度梯度影响。而颗粒速度梯度沿下行床轴向先减小后增大然后趋于稳定,所以Kutta-Joukowski横向力出现以上分布特征。
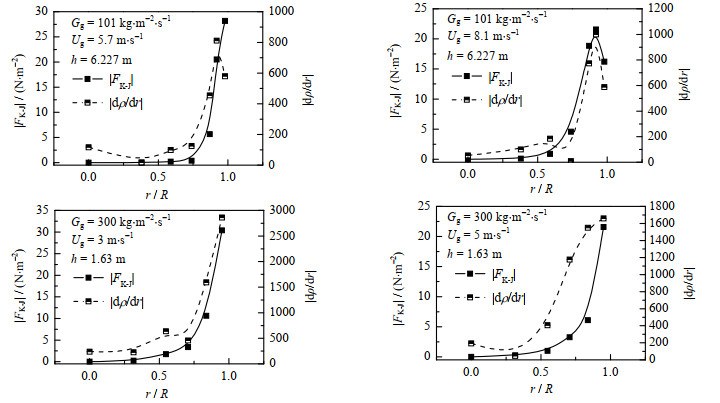
5.4 表观气速对Kutta-Joukowski力的影响图 9为不同表观气速下Kutta-Joukowski横向力和颗粒浓度梯度沿下行床径向的分布。可以看出,Kutta-Joukowski横向力随表观气速的增大而减小。这是因为表观气速增加,各径向位置的颗粒浓度随之减小,颗粒之间的动量交换减弱,导致颗粒速度径向不均匀程度减小——即颗粒速度梯度减小,从而使Kutta-Joukowski横向力减小。
|
图 9 表观气速对Kutta-Joukowski力的影响 Fig.9 Effects of superficial gas velocity on Kutta-Joukowski force |
图 6~9均表明Kutta-Joukowski横向力在下行床中心处为零,且与浓度梯度的变化特征相似。在下行床中心处,由于颗粒速度沿轴线对称,所以速度梯度为零,因此该位置对应的Kutta-Joukowski力为零,与计算结果吻合。沿下行床径向,Kutta-Joukowski横向力与颗粒浓度梯度有相同变化趋势。在图 6~9中,Kutta-Joukowski力与浓度梯度的曲线会出现“波动”。主要是因为WANG等[3, 5-6]和ZHANG等[4, 19]实验中颗粒速度、浓度沿径向的分布会出现局部“波动”,这些“波动”的存在使Kutta-Joukowski力与浓度梯度计算时出现误差。但是,误差的存在并不影响Kutta-Joukowski横向力与浓度梯度变化特征的一致性,不会影响研究结果。
5.5 下行床内Kutta-Joukowski力径向分布的经验关联下行床内Kutta-Joukowski横向力的分布主要受颗粒循环强度、表观气速、颗粒浓度梯度、下行床直径、气体运动黏度、径向位置、轴向位置影响,所以局部Kutta-Joukowski横向力的函数形式可假设为
| $ F_{\mathrm{K}-\mathrm{J}}=\int\left(U_{\mathrm{g}}, G_{\mathrm{s}}, D, \mathrm{d} \rho / \mathrm{d} r, \mu, r / R, h / H\right) $ | (18) |
将各参数进行无量纲化后可得如下表达式:
| $ \frac{F_{\mathrm{K}-\mathrm{J}}}{R U_{\mathrm{g}}^{2}}=a\left(R e_{\mathrm{ap}}\right)^{\mathrm{b}}\left(R e_{\mathrm{ag}}\right)^{\mathrm{c}}\left(\frac{\mathrm{d} \rho}{\mathrm{d} r}\right)(1-r / R)^{\mathrm{d}}(h / H)^{\mathrm{e}} $ | (19) |
根据文献数据,用该式对下行床内局部Kutta-Joukowski横向力的径向分布进行关联,得到经验关联式。
(1) 下行床内颗粒浓度呈“环-核结构”分布——以WANG等[3, 5-6]实验为例。
| $ r / R \leqslant 0.707: \\F_{\mathrm{K}-\mathrm{J}}=143.942 R U_{\mathrm{g}}^{2}\left(R e_{\mathrm{ap}}\right)^{1.658}\left(R e_{\mathrm{ag}}\right)^{-2.272}\left(\frac{\mathrm{d} \rho}{\mathrm{d} r}\right)(1-r / R)^{-0.276}(h / H)^{0.047} $ | (20) |
| $ r / R>0.707: \\ F_{\mathrm{K}-\mathrm{J}}=7858371756 R U_{\mathrm{g}}^{2}\left(R e_{\mathrm{ap}}\right)^{-0.382}\left(R e_{\mathrm{ag}}\right)^{-2.585}\left(\frac{\mathrm{d} \rho}{{\rm d}_{\mathrm{r}}}\right)(1-r / R)^{-0.631}(h / H)^{0.618} $ | (21) |
(2) 下行床内颗粒浓度呈“环-核结构”及“反环-核结构”分布——以ZHANG等[4, 19]实验为例。
| $ r / R \leqslant 0.59: \\ F_{\mathrm{K}-\mathrm{J}}=0.034 R U_\mathrm{g}^{2}\left(R e_{\mathrm{ap}}\right)^{-0.803}\left(R e_{\mathrm{ag}}\right)^{0.184}\left(\frac{\mathrm{d} \rho}{\mathrm{d} r}\right)(1-r / R)^{-0.147}(h / H)^{0.400} $ | (22) |
| $ r / R>0.59: \\ F_{\mathrm{K}-\mathrm{J}}=66382.86 R U_\mathrm{g}^{2}\left(R e_{\mathrm{ap}}\right)^{-1.299}\left(R e_{\mathrm{ag}}\right)^{-0.820}\left(\frac{\mathrm{d} \rho}{\mathrm{d} r}\right)(1-r / R)^{-0.258}(h / H)^{0.490} $ | (23) |
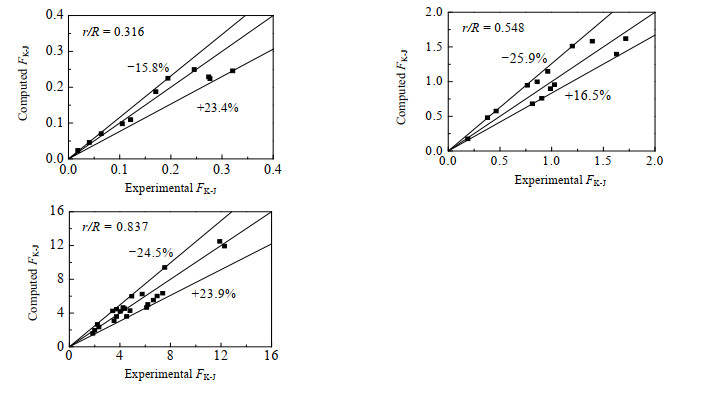
由经验公式计算得到的Kutta-Joukowski横向力与实验值的对比见图 10,计算值与实验值的最大误差为25.9%,可供工程设计参考。
|
图 10 Kutta−Joukowski力计算值和实验值的对比 Fig.10 Comparison of Kutta−Joukowski force between calculated and experimental data |
本文分析了WANG等[3, 5-6]和ZHANG等[4, 19]实验中下行床颗粒浓度径向分布不均匀结构;同时用流体运动方程分析了局部气速的径向分布特征,理论分析的结果与前人实验结果一致。将空气动力学的Kutta-Joukowski定理“移植到”两相流分析中,用Kutta-Joukowski横向力解释了下行床颗粒浓度的不均匀分布。结合目前公开发表的文献数据,分析了下行床Kutta-Joukowski横向力的分布特征,给出了下行床内Kutta-Joukowski横向力的经验关联式,得到以下结论:
(1) 下行床内颗粒群所受Kutta-Joukowski力可由FK-J =-ρg(νp-νg)(∂p/∂r)r计算,力的方向由浓度较低区域指向浓度较高区域。
(2) 通过引入“移动边壁”,分析了气相、固相速度在r/R ≈ 0-0.96出现极值的原因。下行床内局部气速沿径向先增大后减小。
(3) Kutta-Joukowski横向力在下行床中心处为零,沿径向方向与颗粒浓度径向梯度的分布一致。
(4) 表观气速一定,Kutta-Joukowski力随颗粒循环量增加而增加;颗粒循环量一定,Kutta-Joukowski力随表观气速的增加而减小。
(5) Kutta-Joukowski力的主要影响因素为表观气速、颗粒循环量、浓度梯度、无因次径向、轴向位置。给出了Kutta-Joukowski横向力的经验模型式,可供工程设计参考。
符号说明:
|
|
| [1] |
金涌, 祝京旭, 汪展文, 等. 流态化工程原理[M]. 北京: 清华大学出版社, 2001: 48. JIN Y, ZHU J X, WANG Z W, et al. Fluidization Engineering Principles[M]. Beijing: Tsinghua University Press, 2001: 48. |
| [2] |
WANG Z Q, BAI D R, JIN Y. Hydrodynamics of cocurrent downflow circulating fluidized bed (CDCFB)[J]. Powder Technology, 1992, 70(3): 271-275. DOI:10.1016/0032-5910(92)80062-2 |
| [3] |
WANG C X, LI C Y, ZHU J. A comparison of flow development in high density gas-solids circulating fluidized bed downer and riser reactors[J]. AIChE Journal, 2015, 61(4): 1172-1183. DOI:10.1002/aic.14728 |
| [4] |
ZHANG H, ZHU J X, BERGOUGNOU M A. Hydrodynamics in downflow fluidized beds (1):solids concentration profiles and pressure gradient distributions[J]. Chemical Engineering Science, 1999, 54(22): 5461-5470. DOI:10.1016/S0009-2509(99)00284-5 |
| [5] |
WANG C X. High density gas-solids circulating fluidized bed riser and downer reactors[D]. London: Western University, 2013.
|
| [6] |
WANG C X, ZHU J X, LAN X, et al. Radial solids flow structure in high flux gas-solids circulating fluidized bed downers[J]. Powder Technology, 2016, 301: 848-857. DOI:10.1016/j.powtec.2016.07.027 |
| [7] |
BAI D R, ZHU J X, JIN Y, et al. Internal recirculation flow structure in vertical up-flow gas-solids suspensions Part Ⅰ. A core-annulus model[J]. Powder Technology, 1995, 85(2): 171-177. DOI:10.1016/0032-5910(95)03010-7 |
| [8] |
肖海涛, 祁海鹰, 由长福, 等. 循环流化床气固曳力模型[J]. 计算物理, 2003, 20(1): 25-30. XIAO H T, QI H Y, YOU C F, et al. Theoretical model of drag between gas and solid phase in circulating fluidized bed[J]. Chinese Journal of Computational physics, 2003, 20(1): 25-30. DOI:10.3969/j.issn.1001-246X.2003.01.005 |
| [9] |
李晨.催化裂化提升管颗粒浓度径向分布特性的研究[D].北京: 中国石油大学, 2016. LI C. Radial Distribution of Particle Concentration in Riser[D]. Beijing: China University of Petroleum, 2016. http://cdmd.cnki.com.cn/Article/CDMD-11414-1018700710.htm |
| [10] |
周涛, 杨瑞昌, 张记刚, 等. 矩形管边界层内亚微米颗粒运动热泳规律的实验研究[J]. 中国电机工程学报, 2010, 30(2): 92-97. ZHOU T, YANG R C, ZHANG J G, et al. Experimental study on the thermophoresis movement of submicron[J]. Proceedings of the CSEE, 2010, 30(2): 92-97. |
| [11] |
由长福, 祁海鹰, 徐旭常. Basset力研究进展与应用分析[J]. 应用力学学报, 2002, 19(2): 31-34. YOU C F, QI H Y, XU X C. Progresses and Applications of Basset Force[J]. Chinese Journal of Applied Mechanics, 2002, 19(2): 31-34. DOI:10.3969/j.issn.1000-4939.2002.02.008 |
| [12] |
黄社华, 李炜, 程良骏. 任意流场中稀疏颗粒运动方程及其性质[J]. 应用数学和力学, 2000, 21(3): 265-276. HUANG S H, LI W, CHENG L J. On equation of discrete solid particles motion in arbitrary flow field and its properties[J]. Applied Mathematics and Mechanics, 2000, 21(3): 265-276. DOI:10.3321/j.issn:1000-0887.2000.03.007 |
| [13] |
FAN Y P, LI C, FAN H W, et al. Core-annulus radial solids concentration distribution in riser[J]. Chemical Engineering Science, 2018(192): 318-334. |
| [14] |
ZHAO J F, LI W. An analysis of characteristics of unsteady forces on accelerated particles[J]. Mechanics in Engineering, 1998, 20(3): 43-44. |
| [15] |
王勤辉, 杨秋辉, 吴学成, 等. 多相流中颗粒旋转运动特性的研究进展[J]. 化学工程, 2011, 62(62): 2381-2390. WANG Q H, YANG Q H, WU X C, et al. Research progress of particle rotation characteristics in multi-phase flows[J]. Chemical Engineering, 2011, 62(9): 2381-2390. |
| [16] |
王淑彦, 赵云华, 姜健, 等. 数值模拟颗粒旋转对流化床内气固两相流动特性的影响[J]. 工程热物理学报, 2007, 28(2): 262-264. WANG S Y, ZHAO Y H, JIANG J, et al. Numerical simulations of effect of particle rotation on gas and solid flow behavior in fluidized beds[J]. Journal of Engineering Thermophysics, 2007, 28. DOI:10.3321/j.issn:0253-231X.2007.02.025 |
| [17] |
李晨, 范怡平, 贾海兵, 等. 提升管反应器中颗粒浓度径向分布的力学特性[J]. 过程工程学报, 2016, 16(4): 541-548. LI C, FAN Y P, JIA H B, et al. Mechanical radial distribution of particles concentration in a riser reactor[J]. The Chinese Journal of Process Enginering, 2016, 16(4): 541-548. |
| [18] |
江宏俊. 流体力学[M]. 北京: 高等教育出版社, 1985: 89-97. JIANG H J. Hydromechanics[M]. Beijing: Higher Education Press, 1985: 89-97. |
| [19] |
ZHANG H, ZHU J X. Hydrodynamics in downflow fluidized beds (2):Particle velocity and solids flux profiles[J]. Chemical Engineering Science, 2000, 55(19): 4367-4377. DOI:10.1016/S0009-2509(00)00087-7 |
| [20] |
LI S G, LIN W G, YAO J Z. Local slip velocity in a downer[J]. Particuology, 2003, 1(6): 258-261. DOI:10.1016/S1672-2515(07)60005-0 |
| [21] |
曹春社, 金涌, 俞芷青, 等. 并流下行循环流化床中气固速度剖面以及滑落现象的研究[J]. 化工学报, 1995, 46(2): 180-187. CAO C S, JIN Y, YU Z Q, et al. Gas-solid velocity profiles and slip phenomenon in a cocurrent downflow circulating fluidized bed[J]. Journal of Chemical Industry and Enginering (China), 1995, 46(2): 180-187. |
| [22] |
杨勇林, 金涌, 俞芷青, 等. 气固并流下行快速流化床反应器颗粒运动规律的研究[J]. 石油化工, 1991(11): 765-770. YANG Y L, JIN Y, YU Z Q, et al. Particle flow patterns in a gas-solid cocurrent downflow fast fluidized bed[J]. Petrochemical Technology, 1991(11): 765-770. |
| [23] |
董守平. 高等流体力学[M]. 东营: 中国石油大学出版社, 2006. DONG S P. Advanced fluid mechanics[M]. Dongying: China University of Petroleum Press, 2006: 180-185. |




