热导率是与化合物吸热、放热和热传递相关的基本属性,也是化工、石油能源、制药等领域生产和设计必需的参数之一。烃类化合物组成简单,但用途广泛。因此测定或预测烃类化合物的热导率具有重要意义。热导率的实验测定主要有稳态法[1]和非稳态法[2~4],但实验耗时且误差较大,导致热导率数据较难获取。因此,利用化合物的密度、沸点、熔点、对比温度、偏心因子和黏度等物理性质来估算热导率的经验公式被相继提出[5-10]。然而,由于这些公式缺乏严格的理论依据,误差普遍较大(一般在5%~10%),同时由于公式中的密度、沸点等实验数据缺失也给计算带来不便,因此建立不依赖实验数据的预测模型就显示出其优越性。Latini等[11]使用人工神经网络(artificial neural networks,ANN)方法同时预测烷烃类、酮类和硅烷类计55种化合物的热导率,预测精度较高,但要以对比温度、分子量和偏心因子为参数进行估算。刘万强等[12]采用最佳子集回归方法,建立预测烷烃热导率的4参数多元线性回归模型,该研究不需要实验数据作支撑,但仅限烷烃的预测。时静洁等[13]利用遗传算法以及多元线性回归方法,以178种有机物热导率为样本集建立有机化合物热导率的5参数多元线性预测模型,但模型的复相关系数仅有0.742 2,均方根误差为0.129 3。
本研究拟通过提取烃类分子结构特征描述符,利用大数据挖掘和人工智能算法建立不依赖实验数据的液态烃类热导率精确的预测模型,为烃类化合物热导率提供精准预测模型。
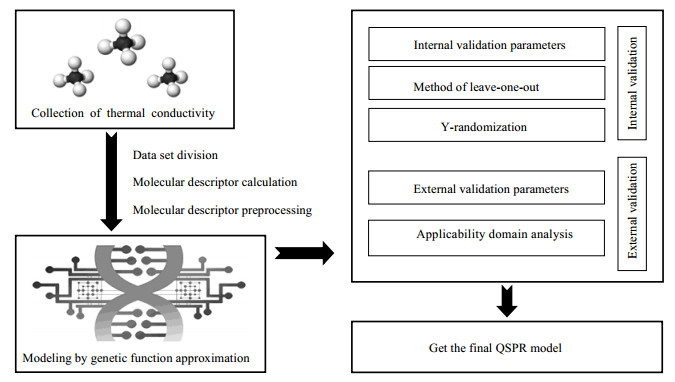
2 方法与步骤研究收集了122种液态烃类化合物在不同温度下的972个热导率数据,采用分层随机化方法对数据集进行划分,然后利用相关软件提取分子描述符。分子描述符经过筛选之后,利用遗传函数近似法构建预测模型,并对建立的预测模型进行内部验证和外部验证。具体建模方法与步骤如图 1所示。
|
图 1 模型构建流程图 Fig.1 Flow chart of prediction model construction |
研究从文献[14]收集了122种开链烃、脂环烃和芳香烃等烃类化合物的热导率数据。烃类的数据统计列于表 1。从表 1中可以看出,热导率λ为0.063~0.189 W·m−1·K−1,温度T为120~580 K,碳原子数从C2到C25,分子量从28.05到338.64,包括开链烃70个、脂环烃20个以及芳香烃32个,不同温度点的数据共计972个。
|
|
表 1 烃类数据集统计信息 Table 1 Hydrocarbon dataset statistics |
分层随机化是将研究对象根据一些重要的特征或因素进行分层,然后根据一定的比例在每一层中随机选取样本分组的方法,该方法可以提高每组样本对总样本特征的代表性,可在数据处理系统(data processing system,DPS)软件中完成[15]。根据傅里叶热传导定律可知,温度是影响热导率的重要因素,因此本研究根据温度进行分层随机划分数据。最终将数据集以7:3的比例划分为含有681个热导率数据的训练集以及含有291个热导率数据的测试集。
2.3 分子描述符的提取与预处理利用GaussView 6.1.1软件[16]构建所有烃类化合物的分子结构,在Gaussian 16 C01[17]中用DFT/B3LYP/6~31(d)方法对分子结构进行优化,将优化好的结构保存为.sdf格式文件,然后导入Dragon 6.0软件[18]中进行分子描述符的提取,获得每个烃类化合物的分子结构描述符。
Dragon 6.0软件可以根据分子结构计算出包括构成、拓扑结构、连接线性、3D-MoRSE描述符、GETAWAY描述符、2D自相关、边缘邻接索引、2D基于矩阵的描述符等共计4 885个分子描述符。
然而,分子描述符过多容易导致参数之间存在共线性等问题,同时参数越多会导致计算量过大,给后续建模带来不便。因此有必要在Dragon 6.0中对众多描述符进行预处理,操作如下:1)排除计算值为常数或接近常数的描述符;2)排除至少缺失一个值的描述符(某些分子的一些描述符无法计算);3)排除相关性大于0.90的描述符。最后保留了382个分子描述符。
2.4 遗传函数近似法构建预测模型遗传函数近似法(genetic function approximation,GFA)是遗传算法(genetic algorithm,GA)和多元自适应回归样条(multivariate adaptive regression spline,MARS)相结合的方法[19],是一种利用生物进化过程(选择、交叉、变异)来生成预测模型的技术。与大多数其他分析算法不同,GFA可以从众多参数中提取参数并建立多种多元线性回归(multiple linear regression,MLR)模型[20]来选择最佳的回归模型。因此本研究采用GFA算法建立热导率的预测模型。
2.4.1 建模算法与流程GA算法是一种通过模拟自然进化过程搜索最优解的计算模型。在GFA算法中,GA中的二进制字符串被基函数所替代,经过选择、交叉、变异,最终得到最优的模型方程。
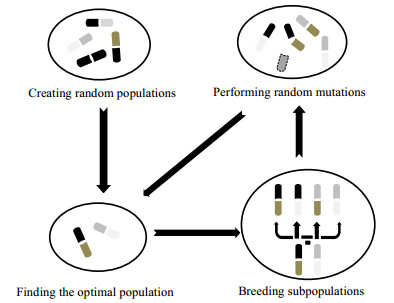
GFA算法过程如图 2所示。1)以群体中的所有分子描述符为对象,随机选择一些特征构建基函数,从这些基函数的随机序列生成初始模型种群。2)根据适应度函数对模型进行评分以找到最佳种群。3)通过对父代种群进行选择和交叉操作来培育子种群,并使用最小二乘回归重新确定新模型的系数。4)通过附加新的随机基函数或移位进行随机变异,以保持模型种群多元化。5)根据模型得分选择最优模型。
|
图 2 遗传函数近似法算法示意图 Fig.2 Schematic diagram of genetic function approximation algorithm |
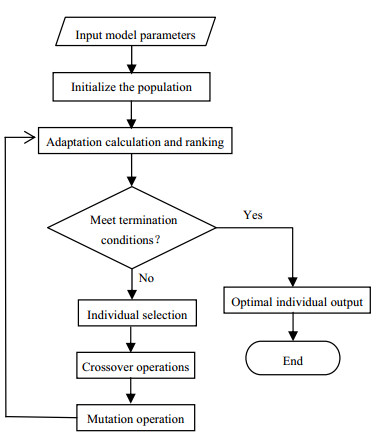
GFA算法建模流程如图 3所示。1)设定模型参数:初始种群数500,最大代数为1 000,突变概率为10%,平滑度参数α=0.5,初始方程长度和最大方程长度分别设置为5和6。2)初始化种群,随机产生500个模型种群。3)通过一个适应度函数来估计个体的质量。研究所用的适应度函数如式(1)所示。4)具有最佳适应度分数的个体更有可能被选择成为父代,并通过对其基函数进行交叉形成子代。5)通过变异操作来保持群体的多样性。6)进行终止条件判断,输出最优模型方程。
|
图 3 遗传函数近似法流程图 Fig.3 Flow chart of genetic function approximation |
根据所给的分子描述符,随机建立多个目标方程,基于一定的拟合标准从父代群体中选取一些个体遗传到下一代群体中,经过一系列的交叉和变异,从而形成新的个体。GFA模型的拟合标准可以在进化过程中使用不同的适应度函数进行评估,如拟合缺失分数(lack-of-fit,LOF)、相关系数的平方R2和调整相关系数的平方Radj2。
由于适应度值是群体中个体生存机会选择的唯一确定性指标,所以适应度函数的形式直接决定着群体的进化行为[13]。3个评估标准中,LOF分数可以有效避免过拟合,并且可以得到最合适的变量数目,使拟合的平滑度得到控制。定义如下:
| ${\rm{LOF}} = \frac{{{\rm{SSE}}}}{{n{{\left[ {1 - \lambda \left( {c + dp'/n} \right)} \right]}^2}}}$ | (1) |
式中:n为训练集样本数量,c为模型的项数,d为自定义平滑度参数;
GFA算法通过遗传算法对可能的预测模型空间进行搜索,利用LOF分数估计每个模型的适应度,从而确立最优模型方程。这种方法不仅可以利用线性多项式建立模型,还可以利用高阶多项式等非线性函数建立模型。与其他方法相比,GFA方法能够自动选择描述符、优化参数,同时建立多个模型种群,从概率上随机寻找目标函数的最优解[21]。
2.5 模型验证模型建立以后,还需要对其进行内部验证和外部验证,以确保模型具有可靠的预测能力。本研究将所有的数据样本按照7:3的比例划分为训练集和测试集。训练集用于内部验证,测试集用于外部验证。如模型的估算值与实验值之间存在良好的一致性,表明模型具有较好的预测能力[22]。
2.5.1 内部验证内部验证常用来评价模型的拟合优度和鲁棒性,其作用是评估基于训练集所建模型的准确性,一般采用的参数为:训练集相关系数的平方Rtraining2、均方根误差(root mean square error,RMSE)。为了评价模型的稳健性,研究还计算了模型中各变量的统计参数,如F值、方差膨胀因子(variance inflation factor,VIF)等。此外,研究还采用“留一法”(leave-one-out,LOO)和Y随机化测试(Y-randomization)方法,对模型进行内部验证。留一法使用交叉验证的均方根误差RMSECV和相关系数QCV2来评估模型是否存在过拟合。如果RMSECV尽可能小,而QCV2大于0.6,则模型在统计上是可靠的[23-24]。
| $ {R^2}_{{\text{training}}} = 1 - \frac{{\sum_{i = 1}^n {{{\left( {{y_i} - {{y'}_i}} \right)}^2}} }}{{\sum_{i = 1}^n {{{\left( {{y_i} - \overline y } \right)}^2}} }} $ | (2) |
| $ {\rm{RMSE}} = \sqrt {\frac{{\sum_{i = 1}^n {{{\left( {{y_i} - {{y'}_i}} \right)}^2}} }}{n}} $ | (3) |
| $ {t_i} = \frac{{{b_i}}}{{\sqrt {{c_{ii}}} \sqrt {\frac{{\sum_{i = 1}^n {{{\left( {{y_i} - {{y'}_i}} \right)}^2}} }}{{n - p - 1}}} }} $ | (4) |
| $ s = \sqrt {\frac{{\sum_{i = 1}^n {{{\left( {{y_i} - {{y'}_i}} \right)}^2}} }}{{n - p - 1}}} $ | (5) |
| $ {\rm{VIF}} = \frac{1}{{\left( {1 - {R^2}} \right)}} $ | (6) |
| $ F = \frac{{{R^2}}}{{1 - {R^2}}}\left( {\frac{{n - p - 1}}{p}} \right) $ | (7) |
式中:yi为热导率实验值,W·m−1·K−1;
Y随机化测试是目前比较常用的一种内部验证方法。它的原理是训练集的因变量(Y矩阵)被随机打乱,而自变量(X矩阵)保持不变,基于随机Y矩阵和原X矩阵建立了一个新的QSPR模型。与原模型相比,所有的随机QSPR模型的R2和Q2的值都应该显著偏低,则说明所建立的QSPR模型是稳健的。同时,本研究还采用参数CRp2作为评价指标,若CRp2的值大于0.5,模型就是可接受的[25]。
| $ C{R_p}^2 = R\sqrt {\left( {{R^2} - R_{\rm{r}}^2} \right)} $ | (8) |
式中:Rr为随机模型的平均相关系数。
Y随机化法测试采用程序包Y-Randomization 1.2 (http://dtclab.webs.com/softwaretools)完成。
2.5.2 外部验证利用测试集数据对模型进行外部验证,用以判断其对于新样本的预测能力。如果模型通过了外部验证,说明模型具有泛化能力,能够用于新化合物性质的预测。
在外部验证中,本研究采用测试集的Rtest2、RMSEP等参数作为验证指标。此外,Roy等[26]引入了一个度量标准rm2来评估QSPR模型的预测能力。如果rm2的值大于0.5,则认为所建立的模型具有很强的预测能力。
| $ r_{\rm{m}}^2 = {r^2}\left( {1 - \sqrt {{r^2} - r_0^2} } \right) $ | (9) |
式中:rm2为外部预测能力验证参数,r02为基于外部数据计算得到的决定系数,r2为预测集的决定系数。
为了进一步验证所建立模型的稳定性和鲁棒性,Kunal等[27]还提出了基于平均绝对误差(mean absolute error,MAE)的准则。所建立模型的MAE应满足以下条件:
MAE ≤ 0.1 ×训练集范围 & MAE + 3 × σ ≤ 0.2 ×训练集范围,其中:
| $ {\rm{Range}}= {y_{\max, {\text{training}}}} - {y_{\min, {\text{training}}}} $ | (10) |
| $ {\rm{MAE}} = \frac{1}{n} \times \sum_{i = 1}^{{n_{\rm{test}}}} {\left| {{y_i} - {{y'}_i}} \right|} $ | (11) |
式中:Range为训练集范围,ymax, training为训练集实验值最大值,ymin, training为训练集实验值最小值,ntest为测试集样本数量,σ为测试集误差值的标准偏差。
此验证可在程序包XternalValidationPlus(http://dtclab.webs.com/softwaretools)中完成。
适用性域(applicability domain,AD)是由分子的结构信息和响应变量定义的空间[28]。研究适用性域是为了评估QSPR模型预测新化合物性质的可靠性。在目前的研究中,使用标准化交叉验证残差R与杠杆值h(帽对角线,hat diagonal)作图的Williams图被用来定义适用性域[29]。在该图中,垂直虚线代表杠杆的临界值h*,水平虚线表示响应的异常值(± 3σ)。第i个化合物的杠杆值hi由描述符矩阵X计算,公式如下:
| $ {h_i} = \mathit{\boldsymbol{X}}_i^{\rm{T}}{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)^{ - 1}}{x_i} $ | (12) |
如果化合物的h值大于阈值h*(h* = 3p/n)但处于−3 ≤ R ≤3的范围内,这个化合物的结构将加强建立的模型。如果大多数数据点位于0 ≤ h ≤ h*和−3 ≤ R ≤3的范围内,那么用于建立模型的数据以及预测值都在适用范围内,并且建立的模型在统计上是可靠的。
3 结果与讨论 3.1 定量预测模型通过遗传函数近似法,得到了一个含有5个分子描述符的线性模型,并且在该模型中再添加一个新参数并不会使其继续优化。所建立的模型如式13所示:
| $ \lambda = 0.004\;4 \times {S_{{\rm{CBO}}}} - 0.010\;5 \times {S_{{\rm{pDiam - B(s)}}}} - 0.000\;27 \times {P_{{\rm{ - VSA - s - 4}}}} - 0.003 \times {R_{{\rm{CON}}}} - 0.000\;2 \times T + 0.251\;3 $ | (13) |
式中:SCBO为常规键序之和,SpDiam-B(s)为频谱直径,来自经本征状态加权的负担矩阵,P-VSA-s-4为P性质的范德华尔斯表面积的数量,RCON为Randic型R-连通性指数。
3.2 预测模型分析 3.2.1 预测模型数据分析所建立的模型中参数的最大VIF值为3.22,说明自变量之间不存在多重共线性。由标准化回归系数的绝对值可知,描述符对热导率的影响程度由大到小依次为SCBO、T、RCON、P_VSA_s_4和SpDiam_B(s)。各描述符的置信度水平P值均远小于0.000 1,说明自变量的可信度高。模型中所涉及描述符的详细参数信息如表 2所示。
|
|
表 2 QSPR模型中所涉及描述符的统计参数 Table 2 Statistical parameters of the involved descriptors in QSPR model |
训练集中,Rtraining2 = 0.913 7,RMSE = 0.005 8,s = 0.005 9,说明所建立的模型具有良好的拟合优度。将所建模型用于测试集中,其Rtest2 = 0.906 9,RMSEP = 0.006 1,说明模型具有良好的泛化能力。模型的F值为1 428.637,说明模型稳健且具有显著的统计学意义。详细的模型参数统计信息如表 3所示。
|
|
表 3 模型参数统计信息 Table 3 Model parameter statistics |
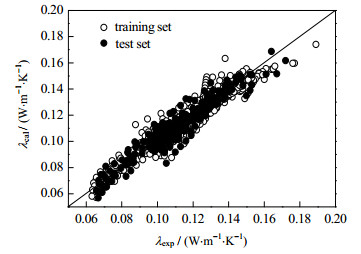
烃类化合物热导率的实验值λexp和计算值λcal比较如图 4所示。数据点基本都处于对角线附近,说明模型具有良好的拟合优度和预测能力。
|
图 4 烃类化合物热导率实验值和计算值 Fig.4 Experimental and calculated thermal conductivity values of hydrocarbon compounds |
用“留一法”和Y随机化测试对模型进行了内部验证。留一法中,参数QCV2 = 0.911 5,大于标准值0.6,RMSECV = 0.02,说明模型稳健可靠。Y随机化测试中,保持自变量X矩阵不变,将训练集的热导率进行60次打乱,模型进行多次Y随机化测试后的R2和Q2的值均远远低于原始模型,其稳定性和可靠性得到验证。此外,参数CRp2= 0.911 0,远大于阈值0.5,说明随机模型的自变量与因变量之间基本不存在相关性,原模型是合理的。rm2= 0.842 4,大于0.5,说明所建模型具有较强的预测能力。
对于所建立的模型,MAE= 0.018 8,训练集范围为7.82,σ = 0.016 5,因此:
MAE ≤ 0.1 ×训练集范围 & MAE + 3 × σ≤ 0.2 ×训练集范围
即0.018 8 ≤ 0.1×7.82 & 0.018 8+3×0.016 5 ≤ 0.2×7.82,所建模型符合基于MAE的准则。
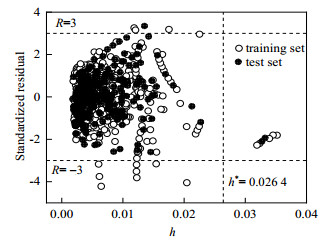
Williams图可以用来对模型的适用性域进行可视化分析,如图 5所示。绝大多数数据点位于0 ≤ h ≤0.026 4(纵向虚线)和−3 ≤ R ≤ 3(横向虚线)的区域内。训练集中有11个数据点(正戊烷320 K、340 K、360 K,乙烯225 K,丙烯180 K,丙烷160 K,联苯560 K,邻三联苯320 K,菲390 K、400 K、410 K)位于横向虚线以外,测试集中有1个数据点(联苯580 K)位于横向虚线以外。此外,训练集和测试集中共有7个数据点(四异丙基二苯甲烷290 K、300 K、310 K、320 K、330 K、340 K和350 K)位于纵向虚线之外。
|
图 5 液态烃类化合物热导率的QSPR模型适用性域 Fig.5 Applicability domain of the QSPR model for thermal conductivity prediction of liquid hydrocarbons |
绝大多数数据点位于纵向虚线与横向虚线形成的区域之内,这说明所建立的模型稳健可靠。训练集中位于横向虚线以外的11个数据点属于异常值,形成原因可能为实验测量误差或文献记载错误。测试集中有1个数据点(联苯580 K)被错误地预测,但是具有较低的杠杆值,这意味着它在模型的适用性范围之内。此外,四异丙基二苯甲烷对应的7个数据点位于h > 0.0264但−3 ≤ R ≤ 3的区域中,这说明该化合物属于在结构上对模型有影响的化合物,能稳定模型,使模型更加精确。结果表明,绝大部分数据点在模型的适用范围之内,这证明了所建立的模型能够准确地估算烃类化合物的热导率[30]。综上所述,本研究所建立的QSPR模型具有良好的拟合优度及较高的精度,是一个具有稳健性和良好预测能力的模型。
3.3 与已有相关工作的比较表 4列出了本研究和其他研究成果的比较。从表中可以看出:1) 本研究建立的模型包含的烃类化合物的数据较多,包含972个数据。2) 预测化合物的种类多。本研究预测模型包括几乎所有的烃类,如烷烃/烯烃/炔烃/脂环烃和芳香烃,这些分子的结构差异较大。3) 计算误差较小。本研究热导率计算结果与实验值的R2仅小于Khajeh等人对于醇类116个样本的值。考虑到本研究的样本数远远大于其他工作的样本数,本研究计算结果依然精确。4) 同时本研究考虑了温度对于热导率的影响。5) 模型验证更充分。本研究采用了内部验证、外部验证对模型进行评估,模型的可靠性、稳健性以及泛化能力得到充分验证。
|
|
表 4 与已有研究成果的比较 Table 4 Comparison on results from references and this study |
在本研究中,用遗传函数近似法建立了烃类化合物热导率的预测模型。
(1) 模型中5个分子描述符对热导率的影响程度由大到小依次为常规键序之和、温度、R-连通性指数、分子内原子的范德华表面积的极化率之和、频谱直径。
(2) 通过模型验证和适用性域分析可知,模型的计算值和实验值基本一致。所建立的预测模型(Rtest2 = 0.906 9,RMSE = 0.006 1)具有良好的预测精度和鲁棒性。
(3) 所建模型可以预测链烃、脂环烃和芳香烃等多类烃类化合物的热导率。
本研究为预测液态烃类化合物的热导率提供了一个稳健的模型,为其他有机物性能数据的估算提供了参考,为有机物性质的预测提供了方法和思路。
| [1] |
YANG I, KIM D, LEE S. Construction and preliminary testing of a guarded hot plate apparatus for thermal conductivity measurements at high temperatures[J]. International Journal of Heat and Mass Transfer, 2018, 122(7): 1343-1352. |
| [2] |
TADA Y, HARADA M, TANIGAKI M, et al. Laser flash method for measuring thermal conductivity of liquids-application to low thermal conductivity liquids[J]. Review of Scientific Instruments, 1978, 49(9): 1305-1314. DOI:10.1063/1.1135573 |
| [3] |
BOUMAZA T, REDGROVE J. Use of the transient plane source technique for rapid multiple thermal property measurements[J]. International Iournal of Thermophysics, 2003, 24(2): 501-512. DOI:10.1023/A:1022928206859 |
| [4] |
KWON S, LEE J, KIM D H. Reliability of thermal conductivity measurement of liquids by using transient hot-wire, photon-correlation spectroscopy and the laser flash method[J]. Journal of the Korean Physical Society, 2016, 68(10): 1145-1155. DOI:10.3938/jkps.68.1145 |
| [5] |
YANG C, ZHAO L, ZHONG C. Correlation of liquid thermal conductivity using molecular connectivity indices[J]. International Journal of Thermophysics, 2003, 24(6): 1651-1665. DOI:10.1023/B:IJOT.0000004097.46622.1a |
| [6] |
BARONCINI C, FILIPPO P D, LATINI G. Thermal conductivity estimation of the organic and inorganic refrigerants in the saturated liquid state[J]. International Journal of Refrigeration, 1983, 6(1): 60-62. DOI:10.1016/0140-7007(83)90036-1 |
| [7] |
NAGVEKAR M, DAUBERT T E. A group contribution method for liquid thermal conductivity[J]. Industrial & Engineering Chemistry Research, 1987, 26(7): 1362-1365. |
| [8] |
MISSENARD F A. Prediction of thermal conductivity for the liquid substances by thermal conductivity at 0℃[J]. Rev Gen Thermodyn, 1973, 141: 751. |
| [9] |
KRAUSS R, STEPHAN K. Thermal conductivity of refrigerants in a wide range of temperature and pressure[J]. Journal of Physical and Chemical Reference Data, 1989, 18(1): 43-76. DOI:10.1063/1.555842 |
| [10] |
KLAAS D M, VISWANATH D S. A correlation for the prediction of thermal conductivity of liquids[J]. Industrial & Engineering Chemistry Research, 1998, 37(5): 2064-2068. |
| [11] |
LATINI G, NICOLA G D, PIERANTOZZI M, et al. Artificial neural network modeling of liquid thermal conductivity for alkanes, ketones and silanes[J]. Journal of Physics Conference Series, 2017, 923(1): 012054. |
| [12] |
刘万强, 陈冠凡, 刘风萍, 等. 烷烃导热率定量构效关系研究[J]. 湖南科技大学学报(自然科学版), 2016, 31(3): 96-101. LIU W Q, CHEN G F, LIU F P, et al. Study on quantitative structure-activity relationship of alkane thermal conductivity[J]. Journal of Hunan University of Science and Technology(Natural Science Edition), 2016, 31(3): 96-101. |
| [13] |
时静洁, 袁雄军, 邵辉. 基于遗传算法对有机物热导率的预测研究[J]. 常州大学学报(自然科学版), 2017, 29(1): 86-92. SHI J J, YUAN X J, SHAO H. Prediction of thermal conductivity of organic compounds based on genetic algorithm[J]. Journal of Changzhou University, 2017, 29(1): 86-92. DOI:10.3969/j.issn.2095-0411.2017.01.015 |
| [14] |
VARGAFTIK N B. Handbook of thermal conductivity of liquids and gases[M]. Boca Raton: CRC Press, 1993.
|
| [15] |
TANG Q. Y, ZHANG C. X. Data Processing System (DPS) software with experimental design, statistical analysis and data mining developed for use in entomological research[J]. Insect Science, 2013, 20(2): 254-260. DOI:10.1111/j.1744-7917.2012.01519.x |
| [16] |
DENNINGTON R, KEITH T A, MILLAM J M. GaussView, revision 6.1[CP]. Shawnee Mission: Semichem Inc, 2016.
|
| [17] |
FRISCH M J, TRUCKS G W, SCHLEGEL H B, et al. Gaussian, revision 16[CP]. Wallingford: Gaussian Inc, 2016.
|
| [18] |
TaleteSrl. Dragon, revision 6[CP]. Milano: Talete Inc, 2014.
|
| [19] |
ROGERS D, HOPFINGER A J. Application of genetic function approximation to quantitative structure-activity relationships and quantitative structure-property relationships[J]. Journal of Chemical Information and Computer Sciences, 1994, 34(4): 854-866. DOI:10.1021/ci00020a020 |
| [20] |
ROY K, ROY P P. Comparative chemometric modeling of cytochrome 3A4 inhibitory activity of structurally diverse compounds using stepwise MLR, FA-MLR, PLS, GFA, G/PLS and ANN techniques[J]. European Journal of Medicinal Chemistry, 2009, 44(7): 2913-2922. DOI:10.1016/j.ejmech.2008.12.004 |
| [21] |
王江, 翟玉玲, 姚沛滔, 等. 基于多目标遗传算法的微通道结构优化[J]. 高校化学工程学报, 2020, 34(4): 1034-1043. WANG J, ZHAI Y L, YAO P T, et al. Structural optimization of microchannels based on multi-objective genetic algorithm[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(4): 1034-1043. DOI:10.3969/j.issn.1003-9015.2020.04.025 |
| [22] |
刘万强, 陆海霞, 刘凤萍, 等. 羧酸酯分子结构有限元分析及液体热导率估算[J]. 高校化学工程学报, 2020, 34(4): 863-869. LIU W Q, LU H X, LIU F P, et al. Finite element analysis of molecular structure and estimation of liquid thermalconductivity of carboxylates[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(4): 863-869. DOI:10.3969/j.issn.1003-9015.2020.04.002 |
| [23] |
CHIRICO N, GRAMATICA P. Real external predictivity of QSAR models: how to evaluate it? Comparison of different validation criteria and proposal of using the concordance correlation coefficient[J]. Journal of Chemical Information and Modeling, 2011, 51(9): 2320-2335. DOI:10.1021/ci200211n |
| [24] |
CHIRICO N, GRAMATICA P. Real external predictivity of QSAR models. Part 2. New intercomparable thresholds for different validation criteria and the need for scatter plot inspection[J]. Journal of Chemical Information and Modeling, 2012, 52(8): 2044-2058. DOI:10.1021/ci300084j |
| [25] |
BEGUM S, ACHARY P G. Optimal descriptor based QSPR models for catalytic activity of propylene polymerization[J]. International Journal of Quantitative Structure-Property Relationships, 2012, 52(8): 2044-2058. |
| [26] |
ROY K, MITRA I, KAR S, et al. Comparative studies on some metrics for external validation of QSPR models[J]. Journal of Chemical Information and Modeling, 2012, 52(2): 396-408. DOI:10.1021/ci200520g |
| [27] |
ROY K, DAS R N, AMBURE P, et al. Be aware of error measures. Further studies on validation of predictive QSAR models[J]. Chemometrics and Intelligent Laboratory Systems, 2016, 152: 18-33. DOI:10.1016/j.chemolab.2016.01.008 |
| [28] |
SAHIGARA F, MANSOURI K, BALLABIO D, et al. Comparison of different approaches to define the applicability domain of QSAR models[J]. Molecules, 2012, 17(5): 4791-4810. DOI:10.3390/molecules17054791 |
| [29] |
CAO L, ZHU P, ZHAO Y, et al. Using machine learning and quantum chemistry descriptors to predict the toxicity of ionic liquids[J]. Journal of Hazardous Materials, 2018, 352: 17-26. DOI:10.1016/j.jhazmat.2018.03.025 |
| [30] |
JAWORSKA J, NIKOLOVA-JELIAZKOVA N, ALDENBERG T. QSAR applicability domain estimation by projection of the training set in descriptor space: a review[J]. Alternatives to Laboratory Animals, 2005, 33(5): 445-459. DOI:10.1177/026119290503300508 |
| [31] |
KHAJEH A, MODARRESS H. Quantitative structure-property relationship prediction of liquid thermal conductivity for some alcohols[J]. Structural Chemistry, 2011, 22(6): 1315-1323. DOI:10.1007/s11224-011-9828-6 |




