2. 中国石油工程建设有限公司华东环境岩土分公司北京咨询中心, 北京 100101
2. Beijing Consulting Center of East China Environmental Geotechnical Branch of China Petroleum Engineering Construction Co. Ltd., Beijing 100101, China
石化安全设备作为保障系统平稳运行的关键环节,在发生关键失效前,需要对设备进行不定期的功能测试,以发现早期失效和可能存在的隐蔽失效,同时避免定期功能测试的各类弊端[1]。制定不定期测试策略的关键是准确估计设备的失效时间,根据测试结果进行备用件配备和必要生产设备切换,防止安全设备不可靠而导致的重大事故。设备失效时间估计主要是对设备历史失效数据的充分挖掘和分析,在可靠性模型基础上对失效时间进行估计[2]。目前已经存在多种可靠性模型,Duane [3]提出模型的随机解释,并将其推广到非齐次泊松过程(nonhomogeneous Poisson process,NHPP)。Peng等[4]在NHPP基础上建立了设备失效时间的估计模型,但是NHPP并未考虑设备维修次数对设备可靠性的累积影响。Kijima等[5]基于设备的役龄提出广义更新过程用于描述不完全维修后设备的可靠度,但是参数复杂难以求解。屈持等[6]提出一种混合Kijima I虚拟役龄模型,考虑了不同失效模式下失效数据之间的差异性。Cha[7]基于NHPP提出广义波利亚过程(generalized Polya process,GPP),GPP拥有良好的数学性能,并反映了先前事件对当前事件发生概率的累积影响,但无法直接将其应用于设备的不完全维修建模中[8]。工程上为了计算简便,利用设备的失效维修数据对设备进行失效时间估计时,维修常常被假设为Weibull分布[9]代表的修复如新和NHPP模型[10]代表修复如旧2种特殊情况。实际上不完全维修更加符合工程实际[11]。本研究在综合考虑模型误差和计算复杂程度的基础上,提出拓展波利亚过程(extension Polya process,EPP)用于描述设备失效到达过程。在EPP的基础上提出设备失效时间估计模型用于估计设备的失效时间,解决传统模型估计设备失效时间存在较大误差和参数复杂难以求解的问题。将EPP模型应用到某催化裂化装置中同工况的6台滑阀设备上进行验证,将所提出的模型与传统模型进行对比,结果表明所提出的模型能在提高估计准确性的同时便于实际工程应用。
2 不完全维修策略下的EPP模型 2.1 失效数据的EPP建模GPP具有良好的数学性能,并且考虑了先前事件对当前状态的影响。GPP将每次事件发生看成一次冲击,每次冲击后会使强度函数产生一个增量。但在通常情况下,修复会改善系统的状态,降低设备的失效强度,所以无法直接利用GPP对设备可靠性进行建模[12]。为此在GPP的基础上提出EPP描述设备失效趋势,并且相比于GPP,提出修复函数的概念,使其能够在修复系统建模的同时更加具有灵活性。
若设备从0时刻开始投入使用,N(t)表示从0时刻到t时刻设备维修的次数。
当EPP描述设备失效的到达过程时,定义其失效强度函数如下:
| $ \lambda (t) = \theta (N(t))(\eta \sigma {t^{\sigma - 1}}) $ | (1) |
式中:
EPP具有较强的灵活性,可以根据不同的修复函数,描述不同类型设备的失效趋势。式(2)为提出的3种类型的修复函数。
| $ \begin{aligned} & \theta(N(t))=(1+N(t) \alpha) \\ & \theta(N(t))=(1+N(t))^\beta \\ & \theta(N(t))=q^{N(t)} \end{aligned}$ | (2) |
式中:α、β、q分别为3种类型修复函数的维修系数。其中当修复函数θ(N(t))=(1+ N(t)α)时,可以较好地描述大多数石化安全设备的失效趋势,对此展开深入研究。
当EPP中修复函数θ(N(t))=(1+ N(t)α)时,失效强度函数用式(3)表示:
| $ \lambda (t)=(1+N(t)\alpha )(\eta \sigma {t}^{\sigma -1}) $ | (3) |
显然,当α=0时,EPP退化成NHPP,当α≠0时,该过程的失效强度函数与维修的次数有关。由于维修可以降低设备的失效率,在接下来的讨论中,均假设α < 0。
设备累计失效次数的期望函数为[13]
| $ E[N(t)] = \sum\limits_{i = 1}^n {iP(N(t) = i) = } \frac{1}{\alpha }({\exp _{}}(\alpha \eta {t^\sigma }) - 1) $ | (4) |
式中:
若由上述累计失效次数的期望函数对t求相应的导数,可以得到等效失效强度函数为
| $ {\lambda _E}(t) = \frac{{d(E[N(t)])}}{{dt}} = \eta \sigma {t^{\sigma - 1}}\exp (\alpha \eta {t^\sigma }) $ | (5) |
定义失效强度函数中包含失效次数,导致失效强度函数具有跳跃性,难以在实际问题中运用。等效失效强度函数为失效期望函数求导得到,使用等效失效强度函数代替定义失效强度函数作为设备失效强度函数可以有效的降低计算的复杂性。
2.2 设备失效维修数据的趋势检验与可靠性模型的选择由于现场情况比较复杂,在收集的设备失效维护数据中,其数据特点可能不满足NHPP或者EPP特性,因此在对失效数据处理前需要对数据进行间隔时间的趋势检验。
采用总时间检验法对数据间隔时间进行趋势检验。若现场有a台设备,m个运行周期,总的运行时间为T,总的失效数为N,ni为每一个运行周期内设备的失效数目,tk为设备第k次失效的时间,分别计算tk/T和k/N,将k/N作为横坐标,tk/T作为纵坐标,绘图将得到散点图。当散点图看不出明显的凹凸性,大致呈一条直线上升时,说明设备失效没有趋势。若散点图的形状为下凹,说明强度函数随着失效次数的增加而降低,散点图形状为上凸,强度函数随着失效次数的增加而增加,失效间隔时间适合使用NHPP或者EPP描述。
利用不同的可靠性模型对数据的间隔时间趋势进行描述时,需要对模型拟合的优良性进行评价。赤池信息准则(akaike information criterion,AIC)常常用于评价分布拟合优度。AIC是基于熵的概念综合衡量了信息复杂度和拟合数据的切合度。AIC值越小,模型选择就越精确,其数学表达式[14]为
| $ \text{AIC} = - 2\max \ln L + 2p $ | (6) |
式中:p为模型中参数的个数,max ln L为对数似然函数的极大值。
2.3 EPP模型的参数估计系统在某时刻开始投入使用,每当系统中设备失效时对设备进行维修。假设设备的无失效运行时间远远大于设备的维修时间,忽略不同维修活动的维修时间,将维修过程看成是点过程[2],可以得到在时间间隔(0,tc)内设备n次失效时间点的次序统计量{t1, t2, t3, …tn},在tc时刻拓展波利亚模型参数集为{σ, η, α}。可以得到失效时间的条件联合概率密度函数为[15]
| $ {f_{\left( {{ N}(t)} \right)}}\left( {{t_1}, {t_2}, \cdots , {t_n}|n} \right) = n!\prod\limits_{i = 1}^n {(\frac{{\alpha \eta \sigma {t_i}^{\sigma - 1}{{\exp }_{}}(\alpha \eta {t_i}^\sigma )}}{{{{\exp }_{}}(\alpha \eta {t_c}^\sigma ) - 1}})} {, _{}}0 < {t_1} < {t_2} < \cdots < {t_n} \leqslant {t_c} $ | (7) |
其中,P[(N(ti+1)−N(ti)=0]表示在区间(ti, ti+1)内无失效发生的概率,tc为设备运行的右截尾时间,ti为最近一次设备失效维修时刻,ti+1为设备下一次失效的失效维修时刻。
对于一个具有参数{σ, η, α}的EPP,其失效数N(t)分布为
| $ P(N({t_c}) = n) = \frac{{\Gamma (1/\alpha + n)}}{{\Gamma (1/\alpha )n!}}{(1 - \exp ( - \alpha \eta {t_c}^\sigma ))^n}{\exp _{}}( - \eta {t_c}^\sigma ) $ | (8) |
其中P(N(tc) = n)代表截止右截尾时间tc,累计发生失效次数为n的概率。
由条件概率公式可以得到失效数据的联合概率密度函数为
| $ \begin{gathered} f\left( {{t_1}, {t_2}, \cdots , {t_n}, n} \right) = {f_{\left( {{T_1}, {T_2}, \cdots , {T_n}|{\rm N}(t)} \right)}}\left( {{t_1}, {t_2}, \cdots , {t_n}|n} \right)P(N({t_c}) = n) = \hfill \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}{\begin{array}{*{20}{c}} {}&{}&{} \end{array}_{}}(\prod\limits_{i = 1}^n {(1 + i\alpha )\eta \sigma {t_i}^{\sigma - 1}} \exp (\alpha \eta {t_i}^\sigma ))\exp ( - (1 + n\alpha )(\eta {t_c}^\sigma )) \hfill \\ \end{gathered} $ | (9) |
采用极大似然估计法对EPP进行参数估计,构造对数似然函数
| $ \ln f\left( {{t_1}, {t_2}, \cdots , {t_n}, n;\eta , \sigma , \alpha } \right) = \sum\limits_{i = 1}^n {({{\ln }_{}}(1 + i\alpha ) + (\sigma - 1)\ln {t_i} + } \ln \eta \sigma + \alpha \eta {t_i}^\sigma ) - (1 + n\alpha )(\eta {t_c}^\sigma ) $ | (10) |
对式(10)中σ、η、维修系数α分别求偏导,得到方程如下:
| $ \begin{array}{*{20}{l}} \frac{{\partial \ln f\left( {{t_1}, {t_2}, \cdots , {t_n}, n;\eta , \sigma } \right)}}{{\partial \eta }} = \frac{n}{\eta } + \sum\limits_{i = 1}^n {\alpha {t_i}^\sigma - {t_c}^\sigma } (1 + n\alpha ) = 0 \hfill \\ \frac{{\partial \ln f\left( {{t_1}, {t_2}, \cdots , {t_n}, n;\eta , \sigma } \right)}}{{\partial \sigma }} = \sum\limits_{i = 1}^n {((\ln {t_i}} ) + (\alpha \eta {t_i}^\sigma \ln {t_i})) + \frac{n}{\sigma } - (1 + n\alpha )(\eta {t_c}^\sigma \ln t) = 0 \hfill \\ \frac{{\partial \ln f\left( {{t_1}, {t_2}, \cdots , {t_n}, n;\eta , \sigma } \right)}}{{\partial \alpha }} = \sum\limits_{i = 1}^n {(\frac{i}{{1 + i}}} + \eta {t_i}^\sigma ) - n\eta {t_c}^\sigma = 0 \hfill \\ \end{array} $ | (11) |
显然上述式子不存在封闭形式的解。采用遗传算法对对数似然函数进行极大化,避免复杂的联立求解从而得到该模型的参数估计。
首先对变量的取值范围进行约束。对于大部分石化安全设备而言,形状参数σ的变化范围为(0,5)。对于尺度参数η,根据定义,η > 0。根据EPP模型,修复因子α有3种情况:α=0对应EPP退化成NHPP,维修对应最小维修;α > 0对应维修增加了设备的失效强度;α < 0对应维修是不完全维修,维修会降低设备的失效强度,并且修复函数的值不能小于0,因此选取−1/n < α < 0对α进行约束。
利用遗传算法对该对数似然函数进行极大化,将负对数似然函数作为遗传算法中的适应度函数。
通过定义上述适应度函数和约束,可以将求解3个复杂不等式的问题转化成遗传算法优化问题,调用遗传算法即可对该优化问题进行求解。约束表达式如下:
| $ s{\text{.}}t\left\{ {\begin{array}{*{20}{c}} {{{\min }_{}}( - \ln f\left( {{t_1}, {t_2}, \cdots , {t_n}, n;\eta , \sigma , \alpha } \right))} \\ { - \frac{1}{n} < \alpha < 0} \\ {\eta > 0} \\ {0 < \sigma < 5} \end{array}} \right. $ | (12) |
每次维修后出现新的失效维修数据,需要重新进行参数估计,动态地更新模型中α、σ、η的值,其后再利用失效估计模型对未来失效时间进行估计。
3 石化安全设备失效时间的估计与测试策略制定对于设备维护而言,从现在时刻开始到下一次设备失效时刻之间的时间称为设备的剩余寿命(remaining useful life,RUL),可以根据历史的设备失效数据,对设备的RUL进行估计。
由于设备失效机制的复杂性与随机性,设备的失效间隔为一个随机变量,对设备失效间隔时间的估计结果表示为一个失效分布,如下:
| $ {{\text{t}}_{i + 1}} - {{\text{t}}_i} = {{\text{x}}_{\text{i}}} \sim {\text{F}}({x_i}|{\rm Z}({\text{t}})) $ | (13) |
式中:xi为设备的第i次失效间隔时间,Z(t)为设备历史失效数据集。首先需要利用设备历史失效数据对模型参数进行估计,之后利用估计模型对未来失效数据进行估计。
由式(4)和(5)已知EPP的失效强度函数,对失效强度函数λ(t)的积分为累计失效强度函数W(t),也为失效期望。
| $ W(t) = E(N(t)) $ | (14) |
给定设备第i次修复在时刻ti结束,则到第i+1次失效时刻前设备的可靠度为
| $ R({t_{i + 1}}|{{\text{t}}_i}) = P(N({t_{i + 1}}) - N({{\text{t}}_i}) = 0) = {\exp _{}}[W({t_{i + 1}}) - W({{\text{t}}_i})] $ | (15) |
式中:
那么可以进一步得到第i+1次失效时间ti+1的条件概率密度函数
| $ \begin{array}{l}f({t}_{i+1}|{\text{t}}_{i})=\underset{\Delta \text{t}\to 0}{\mathrm{lim}}\frac{P(第\text{i}+1次故障发生在[{t}_{i+1}, {t}_{i+1}+\Delta t])}{\Delta \text{t}}\times P(无故障发生在[{\text{t}}_{i}, {t}_{i+1}])=\\ \;\;\;\;\;\;\;\;\;\;\;\;\lambda \left({t}_{i+1}\right)\times {\mathrm{exp}}_{}[W({t}_{i+1})-W({\text{t}}_{i})]\end{array} $ | (16) |
基于EPP模型对设备的RUL进行估计。将已知的ti作为起始时刻,已知进行了i次不完全维修。令t0=ti+1−ti,则F(t0;Z(t))为失效间隔时间分布函数,即从ti时刻开始到第i+1次失效发生时刻,则可以得到可靠度函数R(t)为
| $ \begin{array}{l} R(t) = P(F({t_0}) > t) = {\exp _{}}[W({t_i}) - W({t_i} + t)] = {\exp _{}}[ - \int\limits_{{t_i}}^{{t_i} + t} {{\lambda _E}\left( t \right)dt} ] = \hfill \\ {\begin{array}{*{20}{c}} {}&{} \end{array}_{_{_{}}}}_{}{\exp _{}}( - \int\limits_{{t_i}}^{{t_i} + t} {\eta \sigma {t^{\sigma - 1}}{{\exp }_{}}(\alpha \eta {t^\sigma }))dt} = {\exp _{}}( - (\frac{1}{\alpha }(e{\text{xp(}}\alpha \eta {({t_i} + t)^\sigma }{\text{)}} - 1)(exp(\alpha \eta {t_i}^\sigma ) - 1))) \hfill \\ \end{array} $ | (17) |
当设备历史的失效时间给定时,可以通过计算R(t)分布的期望获得第i+1次失效的平均失效时间,将平均失效时间作为设备的失效间隔时间。
| $ E(F({t_0})) = \int\limits_0^\infty {P(F({t_0}) > t){\text{d}}t = } \int\limits_0^\infty {{{\exp }_{}}( - (\frac{1}{\alpha }(ex{p_{}}(\alpha \eta {{({t_i} + t)}^\sigma }) - 1)(ex{p_{}}(\alpha \eta {t_i}^\sigma ) - 1))){\text{d}}t} $ | (18) |
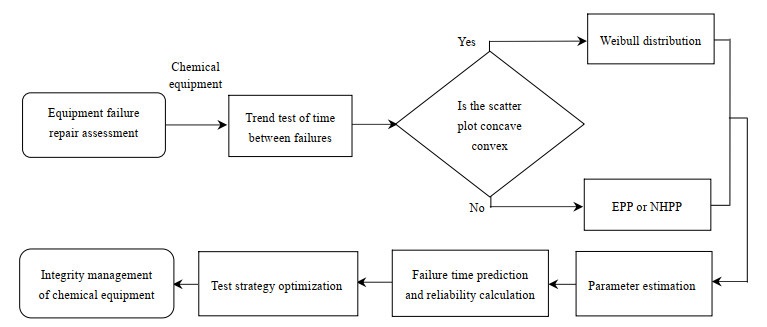
基于EPP模型的石化安全设备功能测试优化流程如图 1所示。
|
图 1 设备功能测试优化流程 Fig.1 Flow chart of optimization process of equipment function tests |
传统的功能测试策略往往是定期测试,并未考虑到设备运行时间和维修次数对可靠性的影响。根据设备的RUL,制定合理的不定期测试策略,可以降低维护的成本,提高功能测试的效率。当设备估计的RUL变化时,不定期功能测试策略相应发生改变。不定期功能测试策略如下:
| $ {T_C} = f \times RUL $ | (19) |
式中:TC为不定期功能测试时间,h;f为预防系数,满足0 < f≤1,推荐预防系数值为0.8~1。
4 案例分析通过分析催化裂化装置中滑阀设备的失效维修数据,从而验证EPP用于描述设备失效趋势的有效性。催化裂化装置结构复杂,需要有效的设备对内部各个变量进行操控,从而保证装置平稳运行。滑阀作为催化裂化装置中的重要设备,能够有效地对装置内部的反应温度和压力、物料流量进行调节。在关键时刻,滑阀能够切断两器的连接,起到关键的保护作用。滑阀设备失效会引起整个催化裂化装置失效,为了保证催化裂化装置的安全平稳运转,对滑阀设备进行可靠性评估至关重要[17]。通过故障模式影响和危害性分析(FMECA)滑阀设备长期在高温高压的极端环境下运行,认为容易发生结构失效,导致催化裂化装置不能安全平稳地运转[18],
如表 1所示,利用Monte Carlo模拟[4]获得了某催化裂化装置中相同工况下6台滑阀设备从2010~2020年在役期间的结构失效时间数据,在此案例中采用运行时间作为失效数据,总的失效数据个数为47个。由于各种原因导致采集的数据存在左截尾或者区间截尾等特殊情况,通常运用相应的填充算法进行预处理,再进行分析计算[6]。设备的总运行时间为87 600 h,即设备运行的右截尾时间。
|
|
表 1 滑阀设备结构失效模式数据表 Table 1 Structural failure data of slide valve equipment |
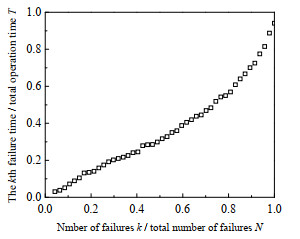
采用失效数据总时间检验法进行失效时间趋势检验,得到总时间检验图如图 2所示。根据曲线的凹凸情况,表明滑阀设备随着时间变化,滑阀设备失效强度减小。
|
图 2 滑阀设备失效数据总时间检验散点图 Fig.2 Scatter diagram of total time inspection for failure data of slide valve equipment |
分别利用Weibull分布,NHPP、EPP描述表 1中47条设备失效数据得到的模型参数估计结果与AIC值见表 2。
|
|
表 2 不同模型的参数及其AIC值的比较 Table 2 Comparison of parameters and AIC values of different models |
由表 2可以看出EPP模型的AIC值最小,表明滑阀失效数据通过EPP模型描述优于Weibull分布和NHPP模型,与工程实际更贴切。通过式(3)、(4)可以得到设备的失效强度函数和累计失效强度函数,比广义更新过程容易得到设备可靠性参数。
将EPP模型、NHPP模型和Weibull分布模型的估计结果与设备失效时间进行比较,验证该模型对石化安全设备失效时间的估计能力。已知催化裂化装置中滑阀设备47次失效时间,可以利用35次失效时间作为历史数据,估计该装置中滑阀设备未来12次失效时间,并与已知的滑阀失效时间进行对比,模型综合估计误差计算如式(20)所示:
| $ S = \sum\limits_{i = 36}^{47} {\frac{{|{\text{PRU}}{{\text{L}}_i} - {\text{RU}}{{\text{L}}_i}|}}{{{\text{RU}}{{\text{L}}_i}}}} /12 $ | (20) |
式中:PRULi为估计第i次失效间隔时间,RULi为实际第i次失效的间隔时间,S为综合估计误差。
表 3中数据为利用不同模型估计得到的失效时间和总的平均估计误差,其中Weibull分布综合估计误差为25.71%,NHPP模型综合估计误差为23.00%,EPP模型综合估计误差为17.25%。EPP模型估计的效果最好,估计的结果也可以接受。结合EPP模型估计的综合误差分析,设备维护人员可以根据企业自身的安全容忍度,将预防系数设置为0.8~1,制定相应的检查、测试和预防性维护(inspection,test,and preventive maintenance,ITPM)策略。对6台滑阀进行统一的功能测试,通过功能测试将即将发生失效的滑阀检测出来,并对滑阀进行维修,将该时刻记录为滑阀设备的失效时刻,防止由于滑阀设备不可靠导致催化裂化装置发生重大事故。
|
|
表 3 设备寿命估计数据 Table 3 Results of equipment life estimation |
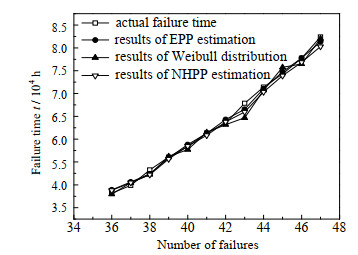
图 3展示了3种模型的估计结果与失效数据结果的对比情况。采用可靠性增长技术等使得设备的可靠性增强,设备失效间隔时间也逐渐延长。由于Weibull分布抽取样本的随机性较大,当出现较大偏差时,会对设备维护产生较大的不利影响,因此Weibull分布不适合用于失效时间估计分析。在进行前4次估计时,NHPP模型和EPP模型的估计结果相差不大,而在进行后8次失效估计时,NHPP模型的估计结果则较为保守,这是因为NHPP模型并未考虑维修次数对设备失效率的影响,忽略维修次数的影响,导致估计误差值将会随着维修次数的增大而增大,不利于维护人员做出正确的判断。EPP模型考虑了设备迭代升级的同时也兼顾了维修次数的影响,估计结果与失效发生时间的误差值较低,并且估计的结果能够随着失效数据的增多越来越准确,能够较好地指导维护。
|
图 3 估计结果与失效数据比较 Fig.3 Comparison of estimated results and failure data |
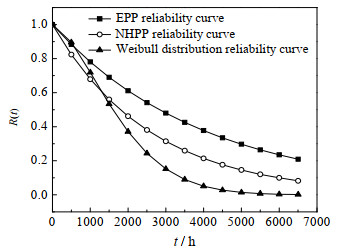
图 4给出了进行第47次维修后EPP模型、NHPP模型和Weibull分布随着时间变化的可靠度曲线,NHPP模型和Weibull分布得到的可靠度曲线相对保守。利用历史47次滑阀设备失效时间,分别得到滑阀设备各类样本第48次失效时间,tWeibull=2 340 h,tNHPP=2 533 h,tEPP=3 783 h。若是采用NHPP模型或者Weibull分布指导滑阀设备进行ITPM策略制定,将设定对六处滑阀设备进行检测的时间为2 000 h左右,以EPP得到的结果,运行2 000 h左右,催化裂化装置中滑阀设备的运行时间远远低于估计失效时间,可能会对企业产生没有必要的测试花费,因此企业可以根据EPP模型的结果,合理调整维护计划,将检测维修时间优化在运行了3 000 h左右,在保证滑阀设备机械完整性水平的同时,降低了维护成本。
|
图 4 第47次维修后可靠度函数曲线 Fig.4 Reliability function curves of equipment after the 47th maintenance |
(1) 基于传统的可靠性模型的维修策略无法准确估计设备失效时间导致检验测试成本过高等问题。所提出的不完全维修情况下的EPP模型,通过AIC判断得到EPP比NHPP和Weibull分布对失效间隔时间数据的拟合性更好。EPP模型比广义更新过程更容易获得失效强度函数、可靠度等可靠性指标。
(2) 对于设备失效时间的估计,EPP模型综合估计误差仅为17.25%,相比于NHPP模型估计误差23.00%和Weibull分布模型估计误差25.71%,分别缩小了5.75% 和8.46%,能够更精确地制定测试策略、降低设备维修成本。
(3) 当数据中存在左截尾,区间截尾和轻度右截尾的情况,运用填充算法后再利用EPP模型也能较好的进行处理。但是当失效维修数据中存在多重右截尾数据情况,通常的处理方式是舍弃多重右截尾数据,这将造成一定程度上的数据浪费。未来考虑可以针对多重右截尾的数据预处理方法与EPP模型的结合。
| [1] |
AIBO Z, TIELING Z, ANNE B, et al. Optimization of maintenances following proof tests for the final element of a safety instrumented system[J]. Reliability Engineering & System Safety, 2020, 196: 106779. |
| [2] |
屈持, 王海清, 刘建利, 等. 基于最小维修的石化安全设备区间截尾寿命数据分析[J]. 化工进展, 2020, 39(11): 4384-4390. QU C, WANG H Q, LIU J L, et al. Interval censored life data of petrochemical safety equipment based on minimal maintenance[J]. Chemical Industry and Engineering Progress, 2020, 39(11): 4384-4390. |
| [3] |
DUANE J T. Learning curve approach to reliability monitoring. IEEE Trans Aero AS-2: 563-566[J]. IEEE Transactions on Aerospace, 1964, 2(2): 563-566. DOI:10.1109/TA.1964.4319640 |
| [4] |
PENG Y, WANG Y, ZI Y Y, et al. Dynamic reliability assessment and prediction for repairable systems with interval-censored data[J]. Reliability Engineering & System Safety, 2017, 159: 301-309. |
| [5] |
KIJIMA M, SUMITA U. A useful generalization of renewal theory: Counting processes governed by non-negative Markovian increments[J]. Journal of Applied Probability, 1986, 23(1): 71-88. DOI:10.2307/3214117 |
| [6] |
屈持, 王海清, 姜巍巍, 等. 不完全维修策略下的安全关键设备可靠性评估[J]. 化工学报, 2021, 72(4): 2328-2336. QU C, WANG H Q, JIANG W W, et al. Reliability evaluation of safety-critical equipment under imperfect maintenance strategy[J]. CIESC Journal, 2021, 72(4): 2328-2336. |
| [7] |
CHA J H. Characterization of the generalized Pólya process and its applications[J]. Advances in Applied Probability, 2014, 46(4): 1148-1171. DOI:10.1239/aap/1418396247 |
| [8] |
FRANCISCO G B, SOPHIE M, CARMENS S. Extensions of the generalized Pólya process[J]. Methodology and Computing In Applied Probability, 2019, 21: 1057-1085. DOI:10.1007/s11009-018-9663-y |
| [9] |
王慧, 赵国超, 宋宇宁, 等. 基于改进的威布尔分布的液压支架可靠性评估方法[J]. 中国安全科学学报, 2018, 28(5): 99-104. WANG H, ZHAO G C, SONG Y N, et al. Reliability evaluation method of hydraulic support based on improved Weibull distribution[J]. China Safety Science Journal, 2018, 28(5): 99-104. |
| [10] |
董航宇, 刘勤明, 叶春明, 等. 基于可靠度的高铁制动机周期预防维修优化研究[J]. 上海理工大学学报, 2020, 42(4): 78-83. DONG H Y, LIU Q M, YE C M, et al. Periodic preventive maintenance optimization and model for high-speed rail brake based on the limitation of reliability[J]. University of Shanghai for Science and Technology, 2020, 42(4): 78-83. |
| [11] |
刘葛辉, 陈绍宽, 金华, 等. 基于延迟时间模型的不完全检修计划优化模型[J]. 浙江大学学报(工学版), 2020, 54(7): 1298-1307. LIU G H, CHEN S K, JIN H, et al. Optimum imperfect inspection and maintenance scheduling model considering delay time theory[J]. Journal of Zhejiang University(Engineering Science), 2020, 54(7): 1298-1307. |
| [12] |
CHA J H, FINKELSTEIN M. Point processes for reliability analysis[M]. Switzerland: Springer Series in Reliability Engineering, 2018.
|
| [13] |
CHA J H, FINKELSTEIN M. Justifying the gompertz curve of mortality via the generalized Polya process of shocks[J]. Theoretical Population Biology, 2016, 109(3): 54-62. |
| [14] |
CHEN X. Using Akaike information criterion for selecting the field distribution in a reverberation chamber[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 55(4): 664-670. |
| [15] |
CHA J H, FINKELSTEIN M. New shock models based on the generalized Polya process[J]. European Journal of Operational Research, 2016, 251(1): 135-141. |
| [16] |
UMMA B, MAA C, OA A, et al. Optimization and estimation in system reliability allocation problem[J]. Reliability Engineering & System Safety, 2021, 212: 107620. |
| [17] |
刘孟德. 催化裂化装置滑阀故障分析[J]. 石油化工设备, 2010, 39(4): 95-99. LIU M D. Fault analysis of slide valve in catalytic cracking unit[J]. Petrochemical Equipment, 2010, 39(4): 95-99. |
| [18] |
潘建欣, 何书默, 肖敏, 等. 基于FMECA方法的车用燃料电池发动机风险评估[J]. 高校化学工程学报, 2020, 34(3): 786-791. PAN J X, HE S M, XIAO M et al. Failure evaluation of vehicle fuel cell engines based on FMECA[J]. Journal of Chemical Engineering of Chinese Universities, 2020, 34(3): 786-791. |




