换热网络综合是通过充分利用冷热流股的能量,实现热回收量最大或年综合费用最低。自1965年HWA[1]提出换热网络的数学模型和最优化问题以来,相关研究得到了长足发展,形成了多种优化模型。
CERDA[2]通过将热物流和热公用工程比拟为货物节点,冷物流和冷公用工程比拟为目的地,热量比拟为仓库,建立了转运模型。YUAN等[3]综合权衡换热单元数、换热面积以及能量回收量三者的关系,较早实现了换热网络年综合费用(total annual costs, TAC)的同步优化。FLOUDAS等[4]将PAPOULIAS和GROSSMANN等[5]的运输模型和FLOUDAS等[6]的超结构模型组合,来确定冷热流股的匹配和换热单元的面积。1990年,YEE和GROSSMANN[7-8]首次建立分级超结构模型,通过预先固定换热单元的连接关系,在每一级中考虑所有的匹配换热可能,形成初始换热网络结构。但是该模型的一些假设会将一些潜在的更优的结构排除在外,而且随着冷热流股匹配关系的增加,优化的复杂程度随之增加。
许多学者针对换热网络的优化模型做了大量改进研究:PARIYANI等[9]提出了公用工程灵活布置的超结构模型,允许公用工程布置在流股的任何位置而不只是末端;陆贞[10]和张勤[11]提出了棋盘模型,简化了网络结构,提高了求解效率;TOFFOLO等[12]提出了一种无约束的拓扑结构,取消对分流分支数和换热单元数量的限制性假设,更大程度发挥算法的自由性;HUANG等[13]建立的非等温混合假设的超结构模型,获得了更低的TAC;HUO等[14-15]建立了一种混合分级超结构模型,有效降低了分流带来的优化难度;PAVÃO等[16]提出了扩展分级超结构模型,允许多公用工程灵活布置在流股的任意分支,扩大了求解域,但复杂程度和求解难度大大增加,其全局最优化也更有挑战性。
非结构模型突破了结构化模型的约束限制,增强了流体匹配的自由性和灵活性,将更多潜在更优的结构包含在求解域,能够更好地发挥启发式算法的随机性优势。但是考察发现,由于非结构模型的随机性,在优化进程中容易出现换热单元交叉,即在同一对冷热流股上,一个换热单元的冷、热流股出口温度等于另一换热单元冷、热流股入口温度的现象。热力学上这种交叉结构是一种不合理匹配,两个换热单元相互制约,影响优化效率。鉴于此,本文提出一种交叉结构禁忌策略,禁止在强制进化随机游走算法(random walk algorithm with compulsive evolution,RWCE)优化中出现交叉结构,以期提高搜索效率及优化质量。
2 换热网络非结构模型 2.1 模型介绍换热网络非结构模型不同于分级超结构模型,该模型不预设固定的框架,冷热流股间可以自由匹配形成任意数量的换热单元,因此能够包含分级超结构模型的所有可能结构。为了提高非结构模型用于化工过程系统的适用性,本文建立一种非结构模型的通用物理表示方式,以2股热流体和2股冷流体算例为例,如图 1示。
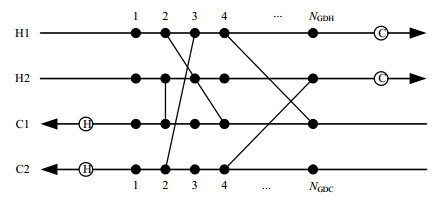
|
图 1 非结构模型结构图 Fig.1 Structure of the non-structural model |
图 1包括5个换热单元,冷热流体流动方式布置为逆流。H1、H2表示2股热流体,C1、C2表示2股冷流体,公用工程布置在冷热流股末端。每股热流体和冷流体上分别预设NGDH和NGDC个产生换热单元的节点,分别用1, …, NGDH和1, …, NGDC表示每个节点的编号。则最大的换热单元数可以达到min{NKH, NKC}(NKH= NGDH·NH; NKC= NGDC·NC)个,NH表示热流体股数,NC表示冷流体股数。在优化时,不同算例对应的NGDH和NGDC数值大小不同。一般情况下,节点数足够大时,即在一股流体上预估换热单元个数最大的数值,在能够满足最多换热单元个数的情况下,节点个数对最终优化结果不会产生大的影响。
2.2 目标函数以年综合费用TAC最低为目标,其中包括冷、热公用工程年费用,换热单元、冷却器、加热器的固定投资费用以及换热单元、冷却器、加热器面积费用。数学描述为:
| $ \min {\rm{TAC}} = \min \sum\limits_{n = 1}^{{N_{\rm{E}}}} {({C_n} + C_n'A_n^{\rm{ \mathsf{ β} }}} ) + \sum\limits_{i = 1}^{{N_{\rm{H}}}} {({C_{{\rm{CU}}}} + C_{{\rm{CU}}}'A_{{\rm{CU}}, i}^{\rm{ \mathsf{ β} }}} ) \\ + \sum\limits_{j = 1}^{{N_{\rm{C}}}} {({C_{{\rm{HU}}}} + C_{{\rm{CU}}}'A_{{\rm{HU}}, j}^{\rm{ \mathsf{ β} }})} + \sum\limits_{i = 1}^{{N_{\rm{H}}}} {{B_{{\rm{CU}}}}{Q_{{\rm{CU}}, i}}} + \sum\limits_{j = 1}^{{N_{\rm{C}}}} {{B_{{\rm{HU}}}}{Q_{{\rm{HU}}, j}}} $ | (1) |
| $ N_{{\rm{h}}, {\rm{c}}}' = \sum\limits_{h = 1}^{{N_{{\rm{KH}}}}} {\sum\limits_{c = 1}^{{N_{{\rm{KC}}}}} {C'{N_{{\rm{h}}, {\rm{c}}}}} } $ | (2) |
| $ C' = \left\{ \begin{array}{l} 0, \;\;\;表示h, c节点处不存在换热器\\ 1, \;\;\;表示h, c节点处存在换热器 \end{array} \right. $ | (3) |
式中,minTAC表示最低年综合费用,前三项分别表示换热单元和冷、热公用工程的固定投资费用和面积费用,后两项表示冷、热公用工程的费用。C分别表示固定投资费用;A表示换热面积;C’表示面积费用系数;β表示面积费用指数;Q表示热负荷;B表示公用工程费用系数;下角标CU表示冷公用工程,HU表示热公用工程;i, j分别表示热流体数和冷流体数,i∈NH,j∈NC;NE可能存在的所有换热单元的个数,Nh, c表示热流体上h节点处和冷流体上c节点处匹配产生的换热单元,N’h, c实际存在的换热单元的个数。
2.3 约束条件(1) 单股冷热流股热平衡:
| $ (T_i^{{{\rm{H}}_{{\rm{in}}}}} - T_i^{{{\rm{H}}_{{\rm{out}}}}}) \cdot {F_{{\rm{Cp}}, i}} = \sum\limits_{n = 1}^{{N_{\rm{E}}}} {{Q_{n, i}}} + \;{Q_{{\rm{CU}}, i}}, \;i \in {N_{\rm{H}}} $ | (4) |
| $ (T_j^{{{\rm{C}}_{{\rm{out}}}}} - T_j^{{{\rm{C}}_{{\rm{in}}}}}) \cdot {F_{{\rm{Cp}}, j}} = \sum\limits_{n = 1}^{{N_{\rm{E}}}} {{Q_{n, i}}} + {Q_{{\rm{CU}}, j}}, \;j \in {N_{\rm{C}}} $ | (5) |
(2) 公用工程热平衡:
| $ (T_n^{{{\rm{H}}_{{\rm{out}}}}} - T_i^{{{\rm{H}}_{{\rm{out}}}}}) \cdot {F_{{\rm{Cp}}, i}} = {Q_{{\rm{CU}}, i}} $ | (6) |
| $ (T_j^{{{\rm{C}}_{{\rm{out}}}}} - T_n^{{{\rm{C}}_{{\rm{out}}}}}) \cdot {F_{{\rm{Cp}}, j}} = {Q_{{\rm{HU}}, j}} $ | (7) |
将RWCE应用于非结构模型优化换热网络,能更好的发挥优化算法的随机性与灵活性。其主要步骤如下。
(1) 种群初始化。随机产生初始种群M1,其中包含N个个体Zi,i= 1, …, N,每个个体对应一个换热网络结构。Qh, c表示种群中每个个体上热流体上的节点与冷流体上的节点匹配产生的换热单元的热负荷,h= 1, …, NH·NGDH, c= 1, …, NC·NGDC;AMH表示换热单元在热流体上的节点编号,AMC表示换热单元在冷流体上的节点编号。非结构的种群初始化过程即为将每个个体对应的冷、热流体节点及换热量都赋初值为0的过程。初始种群表示如式(8)~(10)所示。
| $ {M_1} = {Z_i} \cdot {Q_{{\rm{h}}, {\rm{c}}}} = 0 $ | (8) |
| $ {A_{{\rm{MH}}}} = 0 $ | (9) |
| $ {A_{{\rm{MC}}}} = 0 $ | (10) |
(2) 进化操作。非结构模型中进化阶段分为存在的个体进化及新个体产生2个阶段。
a.存在的个体进化。对种群内部的所有个体进行随机游走操作,其主要方式如式(11)、(12)所示。其中,(Qh, c)it为个体在第it次迭代的初始换热量,(Q’h, c)it为个体随机游走后的换热量,α, β为(0, 1)的随机数,ΔL表示游走的最大步长。个体的进化由控制变量组合实现,一个是个体某一维度上的行走方向1-2αh, c,;另一个是个体在这一维度上的行走步长ΔLβh, c。
| $ {(Q_{{\rm{h}}, {\rm{c}}}')_{{\rm{it}} + {\rm{1}}}} = {({Q_{{\rm{h}}, {\rm{c}}}})_{{\rm{it}}}} + \Delta {Q_{{\rm{h}}, {\rm{c}}}} $ | (11) |
| $ \Delta {Q_{{\rm{h}}, {\rm{c}}}}{\rm{ = }}{Q_{\max}} \cdot \left( {1 - 2{\alpha _{{\rm{h}}, {\rm{c}}}}} \right)\Delta L{\beta _{{\rm{h}}, {\rm{c}}}} $ | (12) |
进化过程中,最小换热量或最小换热面积被作为该换热单元是否存在的临界尺度,如式(13)所示。
| $ Q_{{\rm{h}}, {\rm{c}}}'' \left\{ {\begin{array}{*{20}{l}} {Q_{{\rm{h}}, {\rm{c}}}'}&{{\rm{if}}\;Q_{{\rm{h}}, {\rm{c}}}' > \Delta L\eta }\\ 0&{{\rm{else}}} \end{array}} \right. $ | (13) |
其中,η为保留系数,指可保留的最小换热量与最大游走步长ΔL的比值。由于种群初始化,第一次迭代时,冷、热流体上每一节点处的热负荷均为0,故在第一次迭代时直接跳过存在的个体进化阶段,直接进入下一阶段,新产生换热单元。
b.新个体产生。先随机选择节点,判断该节点处是否存在换热单元,若不存在,则在该位置以一定概率随机生成一定热负荷的换热单元。该操作表示如式(14)~(16)所示。
| $ u = {N_{{\rm{KH}}}} \cdot {\gamma _2};{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} v = {N_{{\rm{KC}}}} \cdot {\gamma _2} $ | (14) |
| $ Q = {Q_{{\rm{max}}2}} \cdot \gamma $ | (15) |
| $ \left\{ {\begin{array}{*{20}{l}} {{Q_{{\rm{u}}, {\rm{v}}}} = Q}&{{\rm{if}}\left( {{Q_{{\rm{u}}, {\rm{c}}}} = 0, {\rm{and}}, {Q_{{\rm{h}}, {\rm{v}}}} = 0} \right)}\\ {u = {N_{{\rm{KH}}}} \cdot {\gamma _1};{\rm{v}} = {N_{{\rm{KC}}}} \cdot {\gamma _2}}&{{\rm{else}}} \end{array}} \right. $ | (16) |
其中,γ,γ1,γ2为0到1之间均匀分布的随机数;u为热流体上节点,v为冷流体上节点,Qu, v为在u,v节点处新生成换热单元的热负荷。
(3) 选择操作。以得到更低的TAC为目标,进行随机游操作。经过it次迭代,若TAC比上一次迭代更低,则接受换热网络结构及每个节点的热负荷,并将该结构的热负荷作为第(it+1)次迭代的初始热负荷,否则不更新该个体,保持第it次迭代的换热网络结构及热负荷。如式(17)所示。
| $ {\left( {{Q_{{\rm{h}}, {\rm{c}}}}} \right)_{{\rm{it}} + 1}} = \left\{ {\begin{array}{*{20}{l}} {{{\left( {{Q_{{\rm{h}}, {\rm{c}}}}} \right)}_{{\rm{it}} + 1}}}&{{\rm{if}}\;F\left( {{{\left( {{{Q'}_{{\rm{h}}, {\rm{c}}}}} \right)}_{{\rm{it}}}}} \right) < F\left( {{{\left( {{Q_{{\rm{h}}, {\rm{c}}}}} \right)}_{{\rm{it}}}}} \right)}\\ {{{\left( {{Q_{{\rm{h}}, {\rm{c}}}}} \right)}_{{\rm{it}}}}}&{{\rm{else}}} \end{array}} \right. $ | (17) |
(4) 变异操作。若经过it次迭代,TAC不低于上一次迭代的费用,则以一定概率δ接受该次迭代的换热网络结构及热负荷,作为第(it+1)次迭代的初始结构及初始换热量。如式(18)所示。
| $ {\left( {{Q_{{\rm{h}}, {\rm{c}}}}} \right)_{{\rm{it}} + 1}} = \left\{ {\begin{array}{*{20}{l}} {{{\left( {{{Q'}_{{\rm{h}}, {\rm{c}}}}} \right)}_{{\rm{it}}}}}&{{\rm{if}}\;F\left( {{{\left( {{{Q'}_{{\rm{h}}, {\rm{c}}}}} \right)}_{{\rm{it}}}}} \right) < F\left( {{{\left( {{Q_{{\rm{h}}, {\rm{c}}}}} \right)}_{{\rm{it}}}}} \right)}\\ {{{\left( {{{Q'}_{{\rm{h}}, {\rm{c}}}}} \right)}_{{\rm{it}}}}}&{{\rm{if}}\;\left( {r < \delta } \right)}\\ {{{\left( {{Q_{{\rm{h}}, {\rm{c}}}}} \right)}_{{\rm{it}}}}}&{{\rm{else}}} \end{array}} \right. $ | (18) |
其中,r为0到1之间均匀分布的随机数,δ为当(it+1)次迭代的TAC大于it次迭代时,更新换热网络结构,接受差解的概率。
(5) 终止条件。记录迭代过程中TAC最低的换热网络结构,当满足终止条件即达到最大迭代次数时,迭代停止。
3.2 交叉结构的影响分析在使用RWCE算法优化非结构模型过程中,确定了冷热流股上的预设节点数NGDH和NGDC后,算法通过从冷热流股上各选取一个节点进行匹配,生成一个换热单元。当同一对冷热流股被再次选取进行匹配产生新的单元时,会出现新的热流体节点在原节点之后,而冷节点在原节点之前的情况,造成同一对冷热流股上,一个换热单元的冷、热流股出口温度大于或等于另一换热单元冷、热流股入口温度的现象。将包含这种匹配的情况称为交叉结构。如图 2示,1号和2号即为两个相互交叉的换热单元。
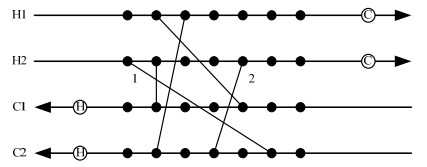
|
图 2 交叉结构图 Fig.2 Schematic diagram of the cross structure |
热力学分析可知:当出现交叉的两个换热单元的热负荷增加到能够充分回收所在流股的能量时,若其他换热单元的热负荷保持不变,则图 2中1号和2号换热单元会相互影响和限制对方的优化进程。优化中若1号热负荷增加,会使得热流体出口温度降低,冷流体出口温度升高,此时2号的热负荷为了达到目标温度,只能向热负荷减小的方向优化,即2号在优化中只能朝减小方向优化。且只有当其减小带来的面积费用减小量大于1号热负荷增加带来的面积费用增加量时,才能继续优化。
以包含13股热流体7股冷流体的算例[18]为例,分析交叉结构对优化进程的影响。观察发现,第413步时产生了交叉结构,将两个交叉的换热单元标记为13和14号,如图 3所示。图 4为13号和14号换热单元在优化中换热负荷变化曲线。从图 4可以看出,13号和14号分别呈现大小交替变化的过程。在优化进程中,当两个交叉的换热单元的热负荷增加到能够充分回收所在流股的能量时,很难再同时增加或减小;为了得到更低的TAC,交叉的2个换热单元需要向相反的方向变化。30 517步以后,14号换热单元消减为0,此时TAC从2 903 218降至2 899 686 $·year-1,减少3 532 $·year-1。
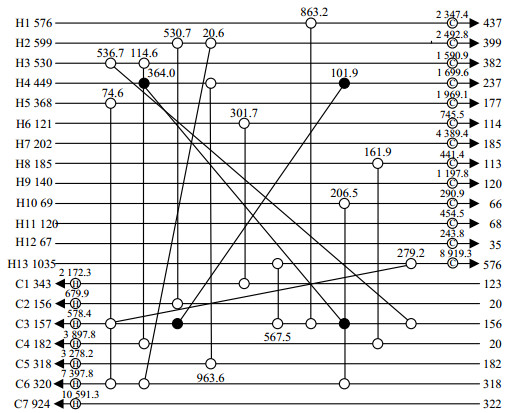
|
图 3 出现交叉结构的换热网络结构图 Fig.3 Schematic diagram of heat exchanger network with cross structure |
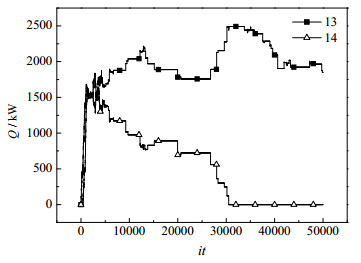
|
图 4 交叉换热单元的换热面积消长情况 Fig.4 Profiles of heat exchange area of cross heat exchanger units |
事实上,优化进程中会出现大量类似的交叉结构,由程序优化进程中记录的数据发现,30 517步以后,程序陆续生成了更多交叉结构,如图 5为该算例同时存在9组交叉结构。由于目前计算所得到的最终优化结果都是不包含交叉结构的,这种不合理的结构的消去往往需要较长计算时间,严重影响了算法优化效率。
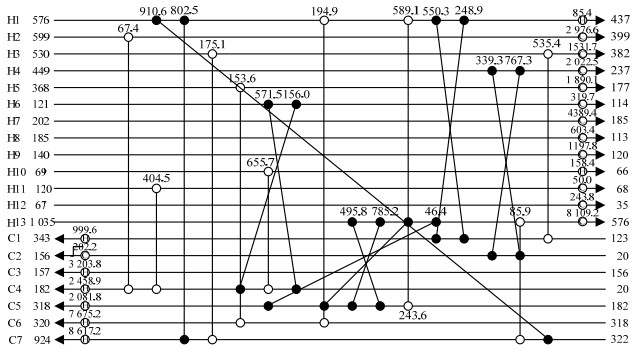
|
图 5 存在9组交叉的换热网络结构图 Fig.5 Schematic diagram of heat exchanger network with 9 sets of cross structures |
以非结构模型为基础的优化中,出现交叉结构会影响优化进程,限制相关联换热单元自由进化,本文提出交叉结构禁忌策略,主要思想是阻止交叉的换热单元生成,从而避免交叉结构的消去对算法优化的影响。具体实现办法是:在个体进化阶段,随机产生新的换热网络结构时,若出现交叉结构,则返回新生成换热单元的位置重新生成换热单元。该算法流程如图 6所示,主要步骤如下:
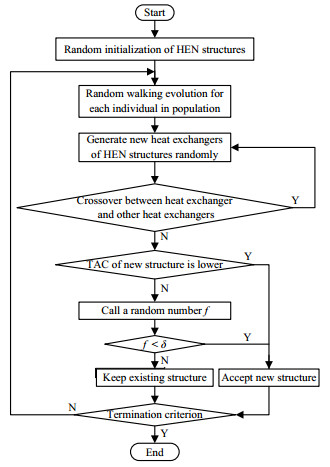
|
图 6 算法流程图 Fig.6 Flowchart diagram of the algorithm |
在新产生个体阶段,先随机产生一定热负荷的换热单元,然后随机选择节点,判断该节点处是否存在换热单元,若不存在,则在该位置生成已选定热负荷的换热单元;若存在,则重新选择节点,直至找到不存在换热单元的节点,生成新的换热单元。生成换热单元之后判断该新生成的换热单元是否与其他换热单元出现交叉。若出现交叉,则返回新生成换热单元的位置重新随机选节点生成换热单元;若没有出现交叉,则继续向下进行。该操作表示如式(19)~(23)所示。
| $ u = {N_{{\rm{KH}}}} \cdot {\gamma _2};v = {N_{{\rm{KC}}}} \cdot {\gamma _2} $ | (19) |
| $ {Q_{{\rm{u}}, {\rm{v}}}} = {Q_{\max 2}} \cdot \gamma $ | (20) |
| $ u/{N_{{\rm{KH}}}} = a \ldots b;u'/{N_{{\rm{KH}}}} = a' \ldots b' $ | (21) |
| $ v/{N_{{\rm{KC}}}} = c \ldots d;v'/{N_{{\rm{KC}}}} = c' \ldots d' $ | (22) |
| $ {Q'_{{\rm{u}}, {\rm{v}}}} = \left\{ {\begin{array}{*{20}{l}} 0&{{\rm{if}}\;a = a', c = c', b > b', d < d'}\\ {{Q_{{\rm{u}}, {\rm{v}}}}}&{{\rm{else}}?} \end{array}} \right. $ | (23) |
其中,γ,γ1,γ2为0到1之间均匀分布的随机数;u,u’为热流体上节点,v,v’为冷流体上节点,a,a’表示节点所在的热流体股数,b,b’表示节点所在热流股上的第几个节点,c,c’表示节点所在的冷流体股数,d,d’表示节点所在冷流股上的第几个节点。Qu, v为在u,v节点处新生成换热单元的热负荷,Q’u, v为判断交叉后u, v节点处的热负荷。
4 算例验证为验证所提策略的有效性,选取不同的算例进行优化,并对优化结果进行比较。
4.1 算例1算例1取自文献[17],包含13股热流体,7股冷流体,流股参数如表 1所示。
|
|
表 1 算例1参数数据 Table 1 Flow parameters of case 1 |
以往文献中优化算例1的方法大多是基于YEE等(1990)[18-20]提出的分级超结构模型进行的。ESCOBAR等[21]采用等温混合假设法,得到算例1的最优结果为1 537 086 $·year-1;PAVÃO等[22]采用改进的粒子群算法,得到的TAC为1 516 482 $/year;BAO等[23]采用保护最优解策略的强制进化随机游走算法,得到的TAC为1 462 363 $·year-1。
本文基于非结构模型,采用强制进化随机游走算法,并禁止交叉结构的生成,优化该算例。将参数设为:NPS = 1,NGDH = 10,NGDC = 10,ΔL = 100,η = 0.2,δ = 0.01,Qmax = 120时,其中,NPS表示种群数,η表示随机游走的概率,δ表示接受差解的概率,Qmax新产生换热单元的最大热负荷。在相同参数下,禁止生成交叉结构的程序比原程序运行得到的TAC更低。采用基于非结构模型的基础RWCE,迭代两千万次,得到算例1的TAC为1 456 589 $·year-1;采用基于非结构模型并禁止生成交叉结构的RWCE,迭代两千万次,得到的优化结果为1 415 994 $·year-1;改进的非结构模型得到的优化结果比原程序减少了40 645 $·year-1。其对应的换热网络结构及优化所得的TAC如图 7、图 8所示。算例的优化结果对比如表 2所示。相比于以往文献中算例的无分流优化结果,本文提出的策略在与其他方法相同的时间内得到了更低的TAC,提高了求解效率,对换热网络优化具有很大的研究意义。
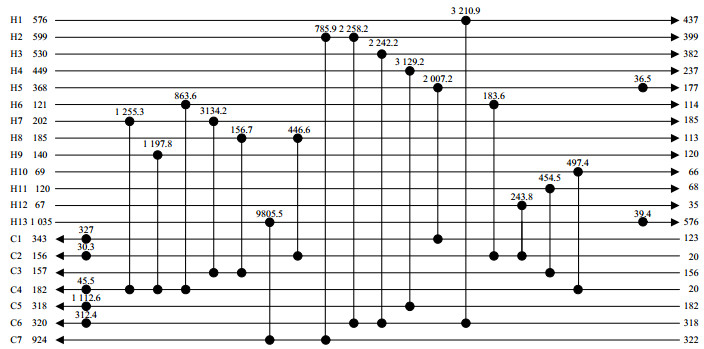
|
图 7 以非结构模型为基础的RWCE优化结果 Fig.7 RWCE optimization results based on the non-structural model |
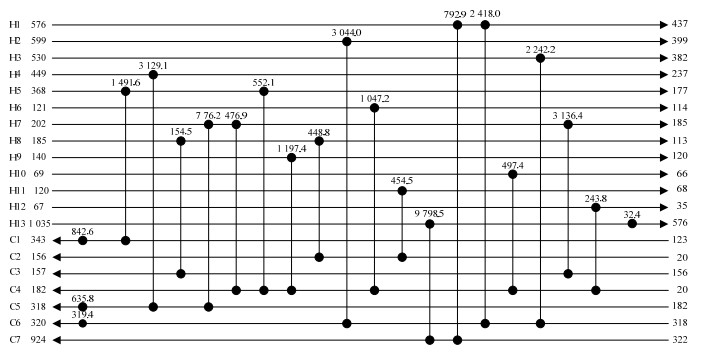
|
图 8 采用交叉结构禁忌策略的RWCE优化结果 Fig.8 RWCE optimization results based on the cross-structure preventive strategy |
|
|
表 2 算例1优化结果对比 Table 2 Comparison of optimized results of case 1 |
算例2的流股数据取自文献[24],为包含10股热流体5股冷流体的换热网络结构,其公用工程及费用公式取自文献[25],具体的数据如表 3所示。
|
|
表 3 算例2参数数据 Table 3 Flow parameters of case 2 |
TRIVEDI (1989)[26]采用“Insert pinch point”法,优化的算例2的TAC为6 019 310 $·year-1;REV等[24]优化算例2得到的TAC为5 613 283 $·year-1。当将参数设为:NPS= 1,NGDH = 10,NGDC = 10,BC = 100,η = 0.05,δ = 0.01,Qmax = 120时,在相同参数下,采用基于非结构模型的基础RWCE,得到算例2的TAC为5 416 186 $·year-1;采用基于非结构模型并禁止生成交叉结构的RWCE得到的TAC为5 233 287 $·year-1;采用交叉结构禁忌策略得到的优化结果比原程序减少了182 899 $·year-1。其对应的换热网络结构及优化所得的TAC分别如图 9、图 10所示。
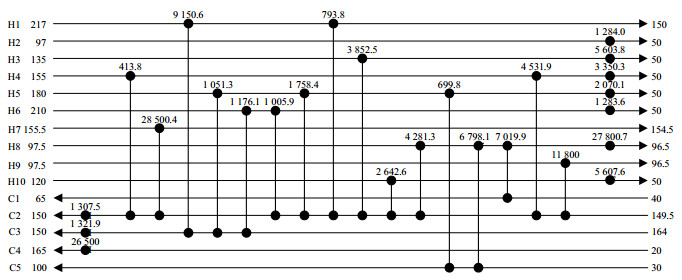
|
图 9 以非结构模型为基础的RWCE优化结果 Fig.9 RWCE optimization results based on the non-structural model |
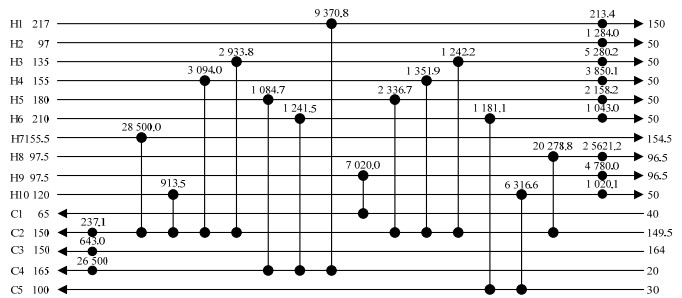
|
图 10 采用交叉结构禁忌策略的RWCE优化结果 Fig.10 RWCE optimization results based on the cross-structure preventive strategy |
|
|
表 4 算例2优化结果对比 Table 4 Comparison of optimized results of case 2 |
由算例1及算例2的优化结果及对比可知,以非结构模型为基础的算法要远好于超结构模型为基础的优化方法。随着系统规模的扩大和实际生产应用的深入,问题的复杂程度不断加大,求解规模和局部最优解的数量随之增加。在相同的目标函数、约束条件和费用系数等条件下,非结构模型能比分级超结构模型得到更优的结果,尤其是改进的非结构模型。而且较优的换热网络结构不存在交叉的换热单元,禁止交叉换热单元的生成,不仅能够加快换热网络结构的进化,极大提高搜索效率,而且能保证优化所得网络结构中每一个换热单元都还保留有极大的进化潜能。
5 结论本文考察了RWCE应用于换热网络非结构模型的优化性能,发现了由于非结构模型的随机性特性,优化过程中容易出现交叉结构的问题。针对这种交叉结构是一种不合理匹配,对寻找换热网络的最优结构有一定的阻碍作用,提出交叉结构禁忌策略进行改进,改善了以非结构模型为基础算法的优化性能。通过两个不同规模的算例对提出策略进行验证,得到的结果分别为1 415 994和5 233 287$·year-1,相同时间内比改进之前分别减少了40 645和182 899 $·year-1。
符号说明:
| Ag | —第g个换热单元的面积,m2 | TiHin | —第i股热流体的入口温度,℃ |
| ACU, i | —第i股热流体上冷公用工程的面积,m2 | TiHout | —第i股热流体的出口温度,℃ |
| AHU, j | —第j股冷流体上热公用工程的面积,m2 | TAC | —年综合费用,$·year-1 |
| BCU, BHU | —分别为冷、热公用工程费用系数 | Zi | —第i个体 |
| Cn, CCU, CHU | ΔTmin | —最小传热温差,℃ | |
| —分别为换热单元和冷、热公用工程的固定投资费用 | ΔL | —游走的最大步长,kW | |
| C’n, C’CU, C’HU | α, γ | — (0, 1)的均匀随机数 | |
| —分别为换热单元和冷、热公用工程的面积费用系数 | β | —面积费用指数 | |
| Fcp, i | —第i股流体的热容流率,kW·℃-1 | δ | —接受差解的概率 |
| Fcp, j | —第j股流体的热容流率,kW·℃-1 | η | —保留系数 |
| M1 | —初始种群 | 下角标 | |
| NC | —冷流体数 | C | —冷流体 |
| NH | —热流体数 | CU | —冷公用工程 |
| NGDC | —每股冷流体上的节点数 | c, v | —冷流体上节点编号 |
| NGDH | —每股热流体上的节点数 | H | —热流体 |
| NKC | —冷流体上的节点总数 | HU | —热公用工程 |
| NKH | —热流体上的节点总数 | h, u | —热流体上节点编号 |
| Qn | —换热单元对应的热负荷,kW | i | —热流体编号 |
| QCU, i | —第i股热流体上的冷公用工程对应的热负荷,kW | j | —冷流体编号 |
| QHU, j | —第j股冷流体上的热公用工程对应的热负荷,kW | in | —入口 |
| (Qh, c)it | —个体在第it次迭代的初始换热量,kW | out | —出口 |
| (Qh, c)it+1 | —个体随机游走后的换热量,kW | 上角标 | |
| Qmax | —求解域的大小,kW | Cin | —冷流体入口 |
| Qh, c | —热流体上h节点与冷流体上c节点匹配产生的换 | Cout | —冷流体出口 |
| 热单元的热负荷,kW | Hin | —热流体入口 | |
| TjCin | —第j股冷流体的入口温度,℃ | Hout | —热流体出口 |
| TjCout | —第j股冷流体的出口温度,℃ | ||
| [1] |
HWA C S. Mathematical formulation and optimization of heat exchanger networks using separable programming[C]//AIChE-l ChemE Joint Meeting. London: AIChE-1 Chem Symp, 1965: 101-106.
|
| [2] |
CERDA J. Transportation models for the optimal synthesis of heat exchanger networks[D]. Pittsburgh: Carnegie-Melon University, 1980.
|
| [3] |
YUAN X, PIBOULEAU L, DOMENECH S. Experiments in process synthesis via mixed-integer programming[J]. Chemical Engineering & Processing Process Intensification, 1989, 25(2): 99-116. |
| [4] |
FLOUDAS C A, CIRIC A R. Strategies for overcoming uncertainties in heat exchanger network synthesis[J]. Computers & Chemical Engineering, 1989, 13(10): 1133-1152. |
| [5] |
PAPOULIAS S A, GROSSMANN I E. A structural optimization approach in process synthesis-Ⅱ. Heat recovery networks[J]. Computers and Chemical Engineering, 1983, 7(6): 707-721. DOI:10.1016/0098-1354(83)85023-6 |
| [6] |
FLOUDAS C A, CIRIC A R, GROSSMANN I E. Automatic synthesis of heat exchanger networks[J]. AIChE Journal, 1986, 32(2): 276-290. DOI:10.1002/aic.690320215 |
| [7] |
YEE T F, GROSSMANN I E, KRAVANJA Z. Simultaneous optimization models for heat integration-I. Area and energy targeting and modeling of multi-stream exchangers[J]. Computers & Chemical Engineering, 1990, 14(10): 1116-1151. |
| [8] |
YEE T F, GROSSMANN I E. Simultaneous optimization models for heat integration-Ⅱ. Heat exchanger network synthesis[J]. Computers & Chemical Engineering, 1990, 14(10): 1118-1165. |
| [9] |
ANKUR P, ABHIGYAN G, PALLAB G. Design of heat exchanger networks using randomized algorithm[J]. Computers & Chemical Engineering, 2006, 30(6-7): 1049-1053. |
| [10] |
陆贞.多股流换热单元网络的综合及衍生约束优化[D].上海: 上海理工大学, 2007. LU Z. Comprehensive and derivative constraint optimization of multi-stream heat exchanger networks[D]. Shanghai: University of Shanghai for Science and Technology, 2007. |
| [11] |
张勤.直接蒙特卡罗/模拟退火混合策略优化换热网络[D].上海: 上海理工大学, 2007. ZHANG Q. Direct Monte Carlo/simulated annealing mixed strategy optimize the heat exchange network[D]. Shanghai: University of Shanghai for Science and Technology, 2007. |
| [12] |
TOFFOLO A. The synthesis of cost optimal heat exchanger networks with unconstrained topology[J]. Applied Thermal Engineering, 2009, 30(17): 3518-3528. |
| [13] |
HUANG K F, Al-MUTAIRI E M, KARIMI I A. Heat exchanger network synthesis using a stagewise superstructure with non-isothermal mixing[J]. Chemical Engineering Science, 2012, 73(19): 30-43. |
| [14] |
HUO Z Y, ZHAO L, YIN H C, et al. Simultaneous synthesis of structural-constrained heat exchanger with and without stream splits[J]. Canadian Journal of Chemical Engineering, 2013, 91(5): 830-842. DOI:10.1002/cjce.21702 |
| [15] |
霍兆义.基于分级超结构的换热网络同步综合与改造方法研究[D].大连: 大连理工大学, 2012. HUO Z Y. Simultaneous synthesis and retrofit of heat exchanger network based on stage-wise superstructure[D]. Dalian: Dalian University of Technology, 2012. |
| [16] |
PAVÃO L V, COSTA C, RAVAGNANI M. An enhanced stage-wise superstructure for heat exchanger networks synthesis with new options for heaters and coolers placement[J]. Industrial & Engineering Chemistry Research, 2018, 57(7): 2560-2573. |
| [17] |
SILVA A P, RAVAGNANI M S, JR E B. Particle swarm optimization applied in retrofit of heat exchanger networks[J]. Computer Aided Chemical Engineering, 2009, 27(9): 1035-1040. |
| [18] |
YEE T F, GROSSMAN I E, KRAVANJA Z. Simultaneous optimization model for heat integration -I. Area and energy targeting and modeling of multi-stream exchangers[J]. Computers & Chemical Engineering, 1990, 14(10): 1151-1164. |
| [19] |
YEE T F, GROSSMAN I E, KRAVANJA Z. Simultaneous optimization model for heat integration-Ⅱ. Heat exchanger network synthesis[J]. Computers & Chemical Engineering, 1990, 14(10): 1165-1164. |
| [20] |
YEE T F, GROSSMAN I E, KRAVANJA Z. Simultaneous optimization model for heat integration-Ⅲ. Process and heat exchanger network synthesis[J]. Computers & Chemical Engineering, 1990, 14(11): 1185-1200. |
| [21] |
ESCOBAR M, TRIERWEILER J O. Optimal heat exchanger network synthesis:A case study comparison[J]. Applied Thermal Engineering, 2013, 51(1/2): 801-826. |
| [22] |
PAVÃO L V, COSTA C B B. Automated heat exchanger network synthesis by using hybrid natural algorithms and parallel processing[J]. Computers & Chemical Engineering, 2016, 94: 370-386. |
| [23] |
BAO Z, CUI G, CHEN J, et al. A novel random walk algorithm with compulsive evolution combined with an optimum-protection strategy for heat exchanger network synthesis[J]. Energy, 2018, 152(c): 694-708. |
| [24] |
REV E, FONYO Z. Diverse pinch concept for heat exchange network synthesis:The case of different heat transfer conditions[J]. Chemical Engineering Science, 1991, 46(7): 1623-1634. DOI:10.1016/0009-2509(91)87010-A |
| [25] |
AHMAD S, LINNHOFF B, SMITH R. Cost optimum heat exchanger networks-2. Targets and design for detailed capital cost models[J]. Computers & Chemical Engineering, 1990, 14(7): 751-767. |
| [26] |
TRIVEDIK K, O'NEILL B K, ROACH J R, et al. A new dual-temperature design method for the synthesis of heat exchanger networks[J]. Computers & Chemical Engineering, 1989, 13(6): 667-685. |




