2. 中国石油大学(北京) 博士后流动站,北京 102249;
3. 中国石油大学(华东) 化学工程学院,山东 青岛 266580;
4. 萨里大学 工程与物理科学学院,萨里 吉尔福德 GU2 7XH
2. Postdoctoral Center of China University of Petroleum, Beijing 102249, China;
3. School of Chemical Engineering, China University of Petroleum, Qingdao 266580, China;
4. Faculty of Engineering and Physical Sciences, University of Surrey, Guildford GU2 7XH, UK
液滴撞壁现象广泛存在于天然气水合物开发、旋风分离、喷雾冷却、喷雾干燥和喷雾燃烧等诸多领域中[1, 2]。其中,以柴油为典型油类的雾化液滴撞壁过程对喷雾控制技术具有重要影响[3, 4]。液滴撞壁后在壁面形成附壁液膜,雾化液滴不再碰撞干壁面,而是碰撞具有附壁液膜的润湿壁面[5]。液滴碰撞附壁液膜相界面结构变化较大,流动机理复杂,且影响因素众多[5, 6],研究液滴碰撞液膜过程不仅有助于预测附壁液膜状况,提升喷雾控制技术,而且对丰富自由界面气液两相流动理论具有重要意义[7]。
近年来,国内外研究者对液滴碰撞液膜现象进行了一定研究。实验方面,Manzello等[8]采用高速摄像仪观测了液滴碰撞液膜润湿壁面过程,揭示了液滴的碰撞速度、液膜厚度和液膜物性对液滴运动形态的影响。Okawa等[9]探讨了液滴碰撞液膜后的运动形态变化以及二次雾化现象。Rioboo等[10]对液滴碰撞液膜润湿壁面的皇冠射流和飞溅运动形态进行了可视化实验,发现皇冠射流的形成与碰撞速度和液膜厚度有关。郭加宏等[11]观测了液滴碰撞液膜润湿壁面的射流和飞溅现象,获得了液滴撞壁后运动形态随液滴碰撞速度、黏度、表面张力、初始直径和液膜厚度的变化规律。
液滴碰撞液膜实验研究的侧重点集中在其自由界面形态变化上,往往难以揭示撞击过程中液膜内的特殊微细现象,同时,受实验条件制约,实验所采用撞壁控制参数的范围相对有限。数值模拟能够从压力场、速度场和温度场等角度揭示液滴碰撞液膜的流动传热机理,且工况参数范围不受实验条件限制,已成为液滴碰撞液膜自由界面气液两相流动研究的重要手段。Shi等[12]采用Lattice Boltzmann Method (LBM)法数值研究了单液滴撞击液膜过程,获得了液滴的沉积、皇冠射流和飞溅等现象。马理强等[13]采用改进的光滑粒子动力学(SPH,Smoothed Particle Hydrodynamics)方法分析了液滴碰撞液膜飞溅条件,探讨了Weber数和表面张力对液滴碰撞液膜的影响。Lee等[14]采用Level-set法研究了Weber数、Ohnesorge数和无量纲液膜厚度对液滴碰撞液膜撞击动力学特征的影响。梁刚涛等[15]采用CLSVOF法研究了液滴碰撞液膜润湿壁面射流形成与飞溅现象。
目前,有关液滴碰撞液膜的形态转捩规律还不完善,撞击过程中流动传热和飞溅机理的揭示仍存在不足,液滴碰撞液膜传热特性的研究还十分缺乏。因此,本文采用CLSVOF法[16]建立液滴碰撞液膜数值模型,开展实验研究验证模型可靠性,分析碰撞速度对液滴运动形态的影响,揭示液滴碰撞液膜流动传热和飞溅机理,并探索液滴撞击液膜动力学及传热特性随碰撞速度的变化规律。
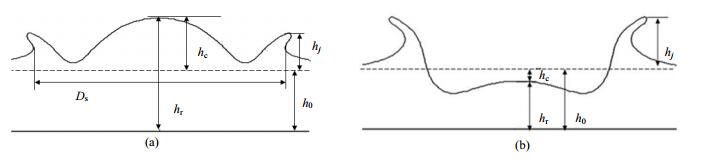
2 数值计算方法液滴碰撞附壁液膜的几何模型如图 1所示。定义D0为液滴的初始直径,Ds是液滴的铺展直径,hj是射流高度,h0是液膜厚度,hr是液面中心高度,hc = hr-h0是液面中心相对高度。hc > 0时,说明液面中心高度大于初始液膜高度,如图 1(a)所示;hc < 0,说明液面中心高度小于初始液膜高度,如图 1(b)所示。铺展系数f、无量纲初始液膜厚度χ,无量纲射流高度
|
图 1 液滴碰撞附壁液膜的几何模型 Fig.1 Geometry model of droplet impact on a liquid film |

|
图 2 计算区域及边界条件 Fig.2 Computational domain and boundary conditions |
液滴碰撞附壁液膜过程的连续性方程、动量方程和能量方程可以表示成
| $ \begin{array}{*{20}{c}} {f = {D_s}/{D_0}, \chi = {h_0}/{D_0}, h_j^* = {h_j}/{D_0}, h_c^* = {h_c}/{D_0}}\\ {\nabla \cdot \mathit{\boldsymbol{v}} = 0} \end{array} $ | (1) |
| $ \frac{\partial }{{\partial t}}[\rho (\varphi )v] + \nabla \cdot [\rho (\varphi )vv] = - \nabla p + \nabla \cdot [\mu (\varphi )(\nabla v + \nabla {v^T})] + \rho (\varphi )g -F $ | (2) |
| $ \frac{\partial }{{\partial t}}[\rho (\varphi ){c_p}T] + \nabla \cdot [\rho (\varphi ){c_p}{\bf{v}}T] = \nabla \cdot (\lambda \cdot \nabla T) $ | (3) |
式中,v是速度矢量,F是表面张力源项,p是压力,g是重力矢量,
动量方程中表面张力源项采用连续表面力(CSF)模型进行求解[18],并通过引入Heaviside函数进行光滑处理,可以表示成
| $ \mathit{\boldsymbol{F}} = \sigma \kappa \delta (\varphi )\nabla \varphi $ | (4) |
| $ \delta (\varphi ) = \frac{{{\rm{d}}H(\varphi )}}{{{\rm{d}}\varphi }} $ | (4a) |
| $ H(\varphi ) = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varphi <-a\\ \frac{1}{2} + \frac{\varphi }{{2a}} + \frac{1}{{2\pi }}\sin (\frac{{\pi \varphi }}{a})\;\;\;\;\left| \varphi \right| \le-a\\ 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varphi > a \end{array} \right. $ | (4b) |
式中,k是曲率,σ是表面张力系数,
光滑后的密度和黏度分别为:
| $ \rho (\phi ) = {\rho _{\rm{g}}} + ({\rho _{\rm{l}}}-{\rho _{\rm{g}}})H(\phi ) $ | (5) |
| $ \mu (\phi ) = {\mu _{\rm{g}}} + ({\mu _{\rm{l}}}-{\mu _{\rm{g}}})H(\phi ) $ | (6) |
式中下标,g,l分别代表气相和液相。
壁面Marangoni应力,可以表示为
| $ \tau = \frac{{{\rm{d}}\sigma }}{{{\rm{d}}T}}\nabla T $ | (7) |
考虑到液滴碰撞液膜的对称性,计算采用二维轴对称模型。为提高计算精度,对壁面附近区域网格进行自适性加密。为验证网格无关性,采用不同液滴网格数的划分方式对计算区域分别划分并进行计算,当液滴铺展系数随网格数的增加趋于稳定时,选取相应的网格数进行划分,即可保证计算精度,又可节省计算时间和成本。经网格无关性检验,网格数为186000。采用有限体积法对控制方程进行离散,压力速度耦合采用SIMPLE方法,压力求解采用PRESTO!方法,计算单元液相体积分数采用CICSAM[19]方法离散求解,控制方程采用QUICK格式进行离散以减少假扩散提高精度,时间步长△t = 10-6s。经收敛性检验选取△t内迭代次数为100,在该迭代次数内计算结果收敛。
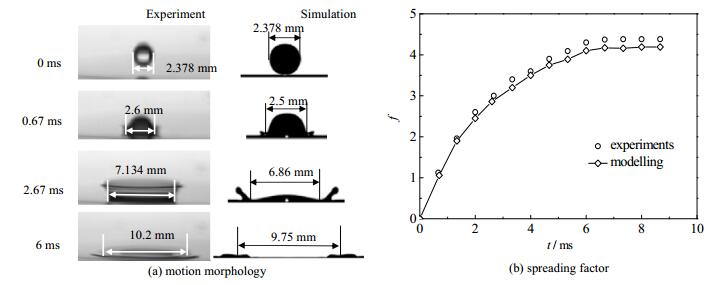
3 计算模型验证为验证模型的可靠性,开展实验研究。实验系统如图 3所示。图 4将液滴碰撞附壁液膜实验与数值模拟结果进行对比,其中,液滴的初始直径D'0= 2.378 mm,碰撞速度U0= 2.1 m·s-1,液膜初始厚度h0= 0.2 mm,壁面静态接触角θe= 30°,液滴温度Td= 345 K,液膜和壁面温度均为300 K。

|
图 3 实验系统示意图 Fig.3 Schematic diagram of the experimental setup 1. high speed camera 2, 11, 15. thermocouple 3. substrate 4. droplet 5. light 6: computer 7. temperature recorder 9. needle 10. sliding support 12. flow control valve 13. liquid tank 14: heater |
|
图 4 液滴碰撞附壁液膜实验和模拟结果对比 Fig.4 Comparison of experimental and simulation results of droplet impact on a liquid film |
对图 4(a)分析可以看出,撞击过程中,数值模拟和实验观测液滴运动形态较为相似,随时间依次呈现出铺展和射流等现象。从图 4(b)可以看出,数值计算所得液滴铺展系数f与实验观测值较为接近,最大误差为4.5%,液滴与液膜接触后,f逐渐增加到最大并趋于稳定。由此可见:本文采用CLSVOF方法所建立的模型能够较为精确地模拟具有复杂强瞬态相界面拓扑结构的液滴碰撞附壁液膜过程。
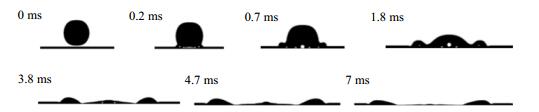
4 数值计算结果 4.1 液滴运动形态图 5是数值模拟液滴碰撞附壁液膜的运动形态,其中,液滴初始直径D0= 2 mm,碰撞速度U0= 1 m·s-1,无量纲液膜初始厚度x = 0.1,壁面接触角θe= 30°,液滴的温度Td= 345 K,液膜和壁面的温度均为300 K。
|
图 5 数值模拟液滴以1 m·s-1碰撞速度碰撞液膜运动形态 Fig.5 Motion morphology for a droplet impacting at 1 m·s-1 |
由图 5可见,液滴与液膜接触后呈铺展状态,铺展边缘处逐渐形成波纹(1.8 ms),并沿壁面径向传播,同时,液膜厚度逐渐减小。随着液滴铺展的持续,碰撞中心处液膜高度逐渐小于铺展边缘(4.7~7 ms)。由于上述液滴运动形态近似波动,因此,称之为波动运动。
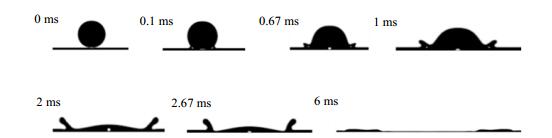
增大液滴碰撞速度到2.1 m·s-1,如图 6所示。液滴与液膜接触后迅速铺展,在铺展边缘处产生射流(0.67 ms),射流高度逐渐增大,射流颈部出现收缩(1~2.67 ms)。随后,射流逐渐落入液膜,撞击中心区域液膜高度逐渐小于铺展边缘区域(2.67~6 ms)。由于上述过程射流特征明显,射流形态近似皇冠形状,因此,称之为皇冠射流运动。需要指出,上述撞击过程形成了射流,但并没有产生飞溅现象。
|
图 6 数值模拟液滴以2.1 m·s-1碰撞速度碰撞液膜运动形态 Fig.6 Motion morphology for a droplet impacting at 2.1 m·s-1 |
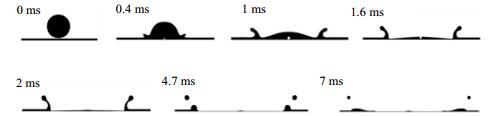
增大液滴的碰撞速度到2.45 m·s-1可见射流飞溅现象,如图 7所示。液滴与液膜接触后迅速铺展并在铺展边缘产生射流(1 ms),随着射流高度的逐渐增加,射流颈部出现收缩并断裂形成破碎液滴(1.6~4.7 ms)。随后,射流逐渐落入液膜(7 ms)。由于上述过程中产生了飞溅,因此,称之为射流飞溅运动。
|
图 7 数值模拟液滴以2.45 m·s-1碰撞速度碰撞液膜运动形态 Fig.7 Motion morphology for a droplet impacting at 2.45 m·s-1 |
继续增大液滴碰撞速度到6 m·s-1,如图 8所示。可以看出,射流内液体有所减小,但其飞溅特征更为明显(0.4~3.8 ms)。
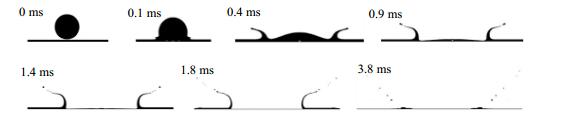
|
图 8 数值模拟液滴以6 m·s-1碰撞速度碰撞液膜运动形态 Fig.8 Motion morphology for a droplet impacting at 6 m·s-1 |
为揭示液滴碰撞液膜运动机理,图 9对不同时刻液滴以6 m·s-1的碰撞速度冲击液膜的压力和速度分布进行分析,其中,压力是静压,液滴初始直径D0= 2 mm,无量纲液膜初始厚度χ = 0.1。

|
图 9 碰撞过程压力和速度分布 Fig.9 Pressure and velocity distribution for a droplet impacting at 6 m·s-1 |
对图 9分析可得,0.4 ms时,受液滴撞击作用,A处(碰撞中心)和B处(液滴和液膜边缘接触点)存在较大的压力,分别是8969和3445 Pa。由于碰撞中心区域液体存在较大的径向压力梯度,因此,液滴的铺展特征明显;B处液体压力与环境大气存在较大的压差,使得铺展边缘区域内液体足够克服表面张力的作用,向外逐渐形成射流。此时,从速度分布可以看出,射流具有较大的速度(6.25 m·s-1),与液滴主体的铺展速度较为接近(5.686 m·s-1),可见,液滴撞击初始阶段,铺展和射流特征均较为明显。0.6 ms时,从压力分布可以看出,A处和B处的压力分别减小到1400和2070 Pa。在射流区域内,射流顶部具有较大的压力(397 Pa)。此时,从速度分布可以看出,射流速度为4.8 m·s-1,大于液滴主体的铺展速度2.43 m·s-1,可见,随着液滴撞击过程的持续,射流逐渐成为主要特征。从速度分布还可以看出,由于液膜内液体沿水平方向流动,铺展边缘区域内液体流入射流后仍具有一定的水平速度,因此,射流具有一定的水平方向运动特征。此外,射流向外扩展的速度远小于撞击区域内液体径向运动速度,因此,在射流区域内产生了速度间断,促进了射流的形成和发展,从而验证了运动间断理论[20]的正确性。
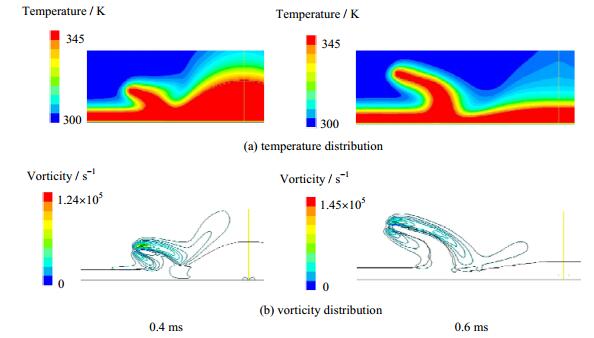
图 10是液滴碰撞液膜不同时刻的温度和涡量分布,其中,液滴温度高于液膜和壁面,液滴向液膜和壁面传热。对图 10(a)进行分析可得,0.4 ms时,A处(碰撞中心)温度梯度为1164 K·mm-1,远大于液滴表面C处(33.86 K·mm-1)和射流顶部D处(260 K·mm-1),这是由于A处传热以液滴与壁面间导热为主,C和D处传热以空气对流传热为主。0.6 ms时,A处的温度梯度减小到1128 K·mm-1,C和D处温度梯度分别减小到31.73和247 K·mm-1。需要指出:A处温度梯度随时间呈减小趋势,考虑到沉积液膜与壁面传热主要为导热,由傅立叶定律可得,壁面热流密度随时间逐渐减小。
|
图 10 碰撞过程温度和涡量分布 Fig.10 Temperature and vorticity distribution for a droplet impacting at 6 m·s-1 |
图 10(b)为液滴碰撞液膜过程中涡量分布,可以看出,撞击过程中不同时刻,射流顶部区域存在较大的涡量,说明,射流顶部空气的剪切作用较大,有助于射流顶部破碎,形成飞溅液滴。
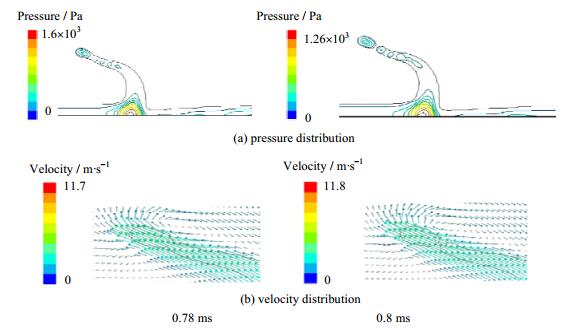
为揭示射流破碎机理,对射流破碎前后不同时刻的压力和速度分布进行分析,如图 11所示。从图 11可以看出,0.78 ms时,射流顶部压力较大(386 Pa),颈部压力较小且与环境空气压力十分接近,说明液体向射流顶部聚集,在表面张力的作用下呈球形,同时,射流颈部产生收缩。0.8 ms时,射流颈部出现破碎,顶部分离的液滴仍具有较大压力。由速度分布可以看出,在射流上侧存在气流漩涡。气流漩涡的存在有助于射流颈部断裂,产生破碎液滴。
|
图 11 液滴破碎飞溅前后射流压力和速度分布 Fig.11 Pressure and velocity distribution for liquid jet breakup |
根据毛细破碎理论,射流破碎的临界毛细波波长可以表示成[21]
| $ {\lambda _{\rm{c}}} = \frac{{2\pi }}{{\sqrt 3 }}{r_{\rm{l}}} $ | (8) |
式中,λc为临界波长,rl为射流颈部半径。由图 11可得,射流颈部半径为0.017 mm,由式8可得,射流破碎临界波长是0.0616 mm。由图 11可得,射流颈部的毛细波波长λs= 0.078 mm。可见,射流颈部毛细波波长大于破碎所需临界波长,因此,射流产生破碎并形成飞溅液滴。
4.3 液滴撞击动力学特性为研究碰撞速度对液滴撞击液膜动力学特性的影响,将不同碰撞速度下液滴铺展系数f表示成时间t的函数,如图 12所示。
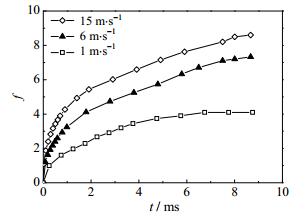
|
图 12 不同碰撞速度下液滴铺展系数随时间的变化 Fig.12 Spreading factor as a function of time at different impact velocities |
从图 12可以看出,不同碰撞速度下液滴铺展系数均随时间逐渐增大。碰撞速度越大,铺展系数越大,当t大约等于8 ms时,不同碰撞速度下液滴的铺展系数均逐渐趋于稳定。
图 13将无量纲射流高度hj*表示成时间t的函数。可以发现,撞壁初始阶段,不同碰撞速度下无量纲射流高度hj*均随时间逐渐增大,当t大约等于2 ms时,不同碰撞速度下无量纲射流高度hj*均达到最大,可见液滴达到最大无量纲射流高度hj, max*所需时间与碰撞速度的相关性较小。碰撞速度越大,无量纲射流高度hj*越大。当U0= 1,6和15 m·s-1时,液滴的最大无量纲射流高度hj, max*分别是0.2,1.16和1.8。从能量的角度来分析,射流产生的原因是由于液滴的撞击动能足以克服液体表面张力做功所造成的,碰撞速度越大,液滴的撞击动能越大,液滴具有克服液体表面张力做功的能力越大,因此,液滴碰撞液膜后射流高度越大。
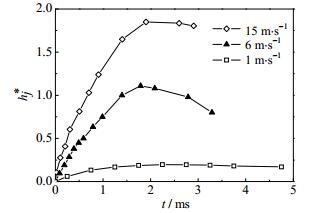
|
图 13 不同碰撞速度下无量纲射流高度的变化 Fig.13 Dimensionless jet height as a function of time at different impact velocities |
图 14对无量纲液面中心相对高度hc*的变化进行分析,可见,撞壁初始阶段,不同碰撞速度下无量纲液面中心相对高度hc*均随时间近似指数递减。hc*减小到最小值后逐渐增加,但hc*的增幅远小于其初始阶段的减幅。碰撞速度越大,无量纲液面中心相对高度的最小值hc, min*越小,且达到hc, min*所需时间越小。从图 14还可以看出,当U0 = 1,6和15 m·s-1时,相应的hc, min*分别是-0.045,-0.09和-0.1,达到hc, min*所需时间分别是4.75,1.79和0.9 ms。其中,当U0= 15 m×s-1时,hc, min*= -0.1,说明,碰撞中心处没有液体存在。由此可见,碰撞速度越大,液滴与壁面间相互作用越明显。
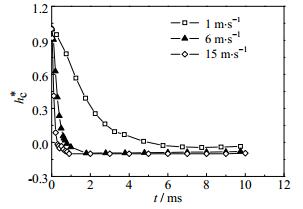
|
图 14 无量纲液面中心相对高度的变化 Fig.14 Dimensionless liquid height as a function of time at different impact velocities |
为研究碰撞速度对液滴撞击液膜传热特性的影响,图 15将不同碰撞速度下液滴撞击区域内壁面平均热流密度q'w表示成无量纲时间t* 的函数,其中t* = tU0/D0。可以看出,不同碰撞速度下q'w随无量纲时间呈现出相似变化。撞壁初始阶段q'w随t* 迅速增加到峰值,这是由于液滴对壁面的冲击扰动迅速增大所造成的。随后,q'w随t* 逐渐减小,分析认为,这是由于,一方面,铺展边缘速度场发生变化,速度逐渐偏向水平方向,与垂直方向的热流场(由液膜指向壁面)间协同程度有所减小;另一方面,液滴与壁面和液膜间的温差随时间也逐渐减小。在上述两方面共同作用下,q'w在达到最大值后逐渐减小。从图 15还可以看出,碰撞速度越大,壁面平均热流密度随无量纲时间的增幅越大,这是由于碰撞速度越大,液滴撞击动能越大,对壁面扰动越大,从而提高了壁面热流密度。
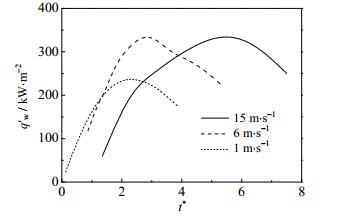
|
图 15 不同碰撞速度下壁面平均热流密度的变化 Fig.15 Average wall heat flux at different impact velocities |
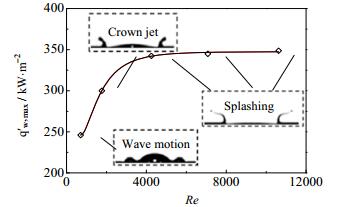
图 16将最大平均热流密度q'w, max表示成雷诺数Re的函数,其中Re为液滴的雷诺数,Re = ρD0U0/μ。可以看出,随着Re的增加,液滴碰撞液膜后由波动运动逐渐过渡到射流飞溅运动,撞击液滴对液膜和壁面的扰动逐渐增大,换热量也相应增加。当Re = 708,1770,4250,7083和10625时,相应的q'w, max分别是245,300,342,345和348 kW·m-2。当Re较小时,q'w, max的增幅较快,当Re大约为4250时,q'w, max随Re的增加逐渐趋于稳定,说明q'w, max的碰撞速度效应随Re的增加逐渐减小。由此可见,在708 < Re < 10625,增加液滴碰撞速度可以促进撞击过程中传热,且Re越小,传热提高越显著。但当Re大于4250时,增加液滴碰撞速度对提高液滴碰撞液膜传热效果不再显著。
|
图 16 最大平均热流密度随雷诺数的变化 Fig.16 Maximum average wall heat flux as a function of Re number |
(1) 液滴接触液膜后,随碰撞速度的增加依次呈现出波动、皇冠射流和射流飞溅等形态。碰撞速度越大,射流飞溅特征越明显,有利于二次雾化液滴的形成。
(2) 碰撞中心较大压力梯度是液滴铺展的主要原因;铺展边缘较大气液压差是产生射流的主要原因;射流区域内速度间断是皇冠射流发展的关键因素;空气剪切及毛细波的作用是射流颈部收缩和产生破碎飞溅的关键。
(3) 碰撞速度越大,液滴的铺展系数和无量纲射流高度越大,无量纲液面中心相对高度越小。
(4) 碰撞速度与壁面热流密度密切相关,碰撞速度越大,壁面最大平均热流密度越大;但随着液滴雷诺数的增加,壁面最大平均热流密度的碰撞速度效应逐渐减小。
| [1] | ZHENG Zhi-wei(郑志伟), LI Da-shu(李大树), QIU Xing-qi(仇性启), et al. Numerical analysis of coupled level set-VOF method on droplet impact on spherical concave surface(液滴碰撞球形凹曲面复合level set-VOF法的数值分析)[J]. Journal of Chemical Industry and Engineering(化工学报), 2015, 66(5): 1667-1675. |
| [2] | YANG Dong-hai(杨东海), HE Li-min(何利民), LUO Xiao-ming(罗小明), et al. Investigation on coalescence characteristics of water droplets in new type electrostatic coalesce(新型静电聚结器中水滴聚结特性研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2012, 26(2): 222-227. |
| [3] | LI Da-shu(李大树), QIU Xing-qi(仇性启), CUI Yun-jing(崔运静), et al. Numerical analysis on impacting velocity effect on spray oil droplet impacting onto a surface during diesel engine cold starting(柴油机冷启动喷雾油滴撞壁速度效应数值分)[J]. Transactions of The Chinese Society of Agricultural Machinery(农业机械学报), 2014, 45(6): 25-31.DOI:10.6041/j.issn.1000-1298.2014.06.005. |
| [4] | LI Da-shu(李大树), QIU Xing-qi(仇性启), YU Lei(于磊), et al. Review of spray droplet impact on a surface(喷雾液滴撞壁研究综述)[J]. Industrial Heating(工业加热), 2014, 43(2): 1-4. |
| [5] | Liang G, Mudawar I. Review of mass and momentum interactions during drop impact on a liquid film[J]. International Journal of Heat and Mass Transfer, 2016, 101: 577-599.DOI:10.1016/j.ijheatmasstransfer.2016.05.062. |
| [6] | Agbaglah G, Thoraval M J, Thoroddsen S T, et al. Drop impact into a deep pool: vortex shedding and jet formation[J]. Journal of Fluid Mechanics, 2015, 764: 1-11.DOI:10.1017/jfm.2014.616. |
| [7] | Wu J, Liu C, Zhao N. Dynamics of falling droplets impact on a liquid film: hybrid lattice Boltzmann simulation[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2015, 472: 92-100. |
| [8] | Manzello S L, Yang J C. An experimental study of a water droplet impinging on a liquid surface[J]. Experiments in Fluids, 2002, 32(5): 580-589.DOI:10.1007/s00348-001-0401-8. |
| [9] | Okawa T, Shiraishi T, Mori T. Production of secondary drops during the single water drop impact onto a plane water surface[J]. Experiments in Fluids, 2006, 41(6): 965-974.DOI:10.1007/s00348-006-0214-x. |
| [10] | Rioboo R, Bauthier C, Conti J. Experimental investigation of splash and crown formation during single drop impact on wetted surfaces[J]. Experiments in Fluids, 2003, 35(6): 648-652.DOI:10.1007/s00348-003-0719-5. |
| [11] | GUO Jia-hong(郭加宏), DAI Shi-qiang(戴世强), DAI Qin(代钦). Experimental research on the droplet impacting on the liquid film(液滴冲击液膜过程实验研究)[J]. Acta Physica Sinica(物理学报), 2010, 59(4): 2601-2609.DOI:10.7498/aps.59.2601. |
| [12] | Shi Z, Yan Y, Fan Y, et al. A lattice Boltzmann method for simulation of a three-dimensional drop impact on a liquid film[J]. Journal of Hydrodynamics, Ser B, 2008, 20(3): 267-272.DOI:10.1016/S1001-6058(08)60056-6. |
| [13] | MA Li-qiang(马理强), LIU Mou-bin(刘谋斌), CHANG Jian-zhong(常建忠), et al. Numerical simulation of droplet impact onto liquid films with smoothed particle hydrodynamics(液滴冲击液膜问题的光滑粒子动力学模拟)[J]. Acta Physica Sinica(物理学报), 2012, 61(24): 244701.DOI:10.7498/aps.61.244701. |
| [14] | Lee S H, Hur N, Kang S. A numerical analysis of drop impact on liquid film by using a level set method[J]. Journal of Mechanical Science and Technology, 2011, 25(10): 2567-2572.DOI:10.1007/s12206-011-0613-7. |
| [15] | LIANG Gang-tao(梁刚涛), SHEN Sheng-qiang(沈胜强), YANG Yong(杨勇). CLSVOF simulation for splashing of single drop impact on flat liquid film(单液滴撞击平面液膜飞溅过程的CLSVOF模拟)[J]. Journal of Thermal Science and Technology(热科学与技术), 2012, 11(1): 8-12. |
| [16] | Yokoi K. A practical numerical framework for free surface flows based on CLSVOF method, multi-moment methods and density-scaled CSF model: numerical simulations of droplet splashing[J]. Journal of Computational Physics, 2013, 232(1): 252-271.DOI:10.1016/j.jcp.2012.08.034. |
| [17] | Kamnis S, Gu S. Numerical modelling of droplet impingement[J]. Journal of Physics D: Applied Physics, 2005, 38(19): 3664-3673.DOI:10.1088/0022-3727/38/19/015. |
| [18] | Brackbill J U, Kothe D B, Zemach C. A continuum method for modelling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335.DOI:10.1016/0021-9991(92)90240-Y. |
| [19] | Ubbink O, Issa R I. A method for capturing sharp fluid interfaces on arbitrary meshes[J]. Journal of Computational Physics, 1999, 153(1): 26.DOI:10.1006/jcph.1999.6276. |
| [20] | Yarin A L, Weiss D A. Impact of drops on solid surfaces: self-similar capillary waves, and splashing as a new type of kinematic discontinuity[J]. Journal of Fluid Mechanics, 1995, 283: 141-173.DOI:10.1017/S0022112095002266. |
| [21] | Shinjo J, Umemura A. Simulation of liquid jet primary breakup: dynamics of ligament and droplet formation[J]. International Journal of Multiphase Flow, 2010, 36(7): 513-532.DOI:10.1016/j.ijmultiphaseflow.2010.03.008. |




