2. 广西石化资源加工及过程强化技术重点实验室,广西 南宁 530004
2. Guangxi Key Laboratory of Petrochemical Resource Processing and Process Intensification Technology, Nanning 530004, China
松脂是松属树木分泌出来的树脂,被誉为“长在树上的石油”。松脂经水蒸汽蒸馏分离可得到松香和松节油。松香广泛应用于胶黏剂、油墨、涂料、造纸施胶剂、合成橡胶、表面活性剂、肥皂、食品、医药和电子等工业领域。松节油为重要有机合成中间体,可用于合成香料、精细化学品等[1]。松脂的蒸馏及其化学加工过程都涉及气液接触和传质传热过程[2-3],因此研究松脂溶液中的气泡运动特性十分必要。
气液两相流广泛存在于能源、动力、化工和冶金等工程领域[4-7],气体通常以气泡的形式分散在液体中。气泡在流体中同时受到表面张力、黏性力、惯性力和浮力的相互作用,会产生不同形状的气泡和运动轨迹。气泡的大小、形状及其运动规律是影响气-液两相流体流动特性的重要参数,也是气液传质设备、化学反应器等设计和操作的重要依据[8],尤其是气泡尺寸的分布、上升速度以及停留时间对于气-液流动与传热传质效果有着直接的联系[9]。流体中气泡的运动行为在工业应用和理论研究中都具有举足轻重的作用。
本文分别采用不同黏度的松脂溶液和二氧化碳作为鼓泡的液相和气相,使用高速相机拍摄不同直径气泡在不同黏度松脂溶液中的上升过程,通过MATLAB数字图像处理对拍摄的图像进行分析处理。实验研究了气泡在不同黏度流体中上升时形状以及气泡纵横比的变化规律,提出了适用于不同黏度体系中的气泡纵横比预测模型。
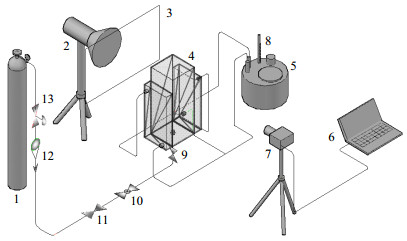
2 实验 2.1 实验装置实验系统主要由气泡稳定发生装置、图像采集装置和恒温系统三大部分组成,实验装置如图 1所示。为了便于观察和拍摄,气泡运动过程在一个尺寸为200 mm × 200 mm × 500 mm的透明有机玻璃容器中完成。容器壁厚5 mm,底部设有气泡注射口,顶部加盖,可以拆卸,既能与大气接触又能保持溶液纯净。容器的两侧各有一个透明夹套,尺寸45 mm × 200 mm × 400 mm。透明夹套通过壁面对角的4个球阀与超级恒温水浴槽连接。水温设定为25℃,水浴温度由精密温度计控制(精度± 0.1℃)。实验气相为CO2气体,由钢瓶提供,依次经过背压阀(图 1,13,下同)、流量计(12)、精密调节阀(11)、球阀(10)和截止阀(9),最后由喷嘴进入液相产生稳压气泡。气泡大小主要取决于喷嘴的内径和气体流量。
|
图 1 实验装置图 Fig.1 Schematic diagram of the experimental setup 1. carbon dioxide cylinder 2. LED light 3. light diffuser 4. bubble column 5. water bath 6. computer 7. high-speed camera 8. thermometer 9. check valve 10. ball valve 11. precision regulating valve 12. rotor flowmeter 13. back pressure |
图像采集系统由高速相机、电脑和光源组成。高速摄影系统为千眼狼2F01型高速相机,高速相机和计算机连接,拍摄的视频储存在计算机中。为了保证图像的清晰,采用逆光拍摄,装置后置有LED灯,为了使光分布均匀,灯前加滤光装置。
实验液相为松脂和松节油溶液,松脂溶液按照松脂和松节油质量比为1:3.75、1:3、1:2.25和1:1.5配制,用符号S1、S2、S3和S4表示该溶液体系。所有溶液的物理性质在25℃下测定,结果如表 1所示。
|
|
表 1 25℃时液相的物理性质 Table 1 Physical properties of solutions at 25℃ |
实验时,调节背压阀使系统压力稳定在一个值,调节精密调节阀使由鼓泡装置产生的单个CO2气泡自喷嘴进入实验段,由高速相机拍摄气泡的上升过程。气泡脱离喷嘴后会产生短暂的振荡,在上升一段距离后由于黏性力和表面张力的作用,气泡速度不再变化,达到平衡状态。调整相机高度,使相机位于气泡喷射点上方200 mm处。溶液高度为350 mm,拍摄高度范围为200 ~250 mm。高速相机以1000 FPS的速率捕获气泡的运动,分辨率为588×497像素,视频通过MATLAB数字图像处理,通过编程得到气泡的运动参数。
2.3 图像分析 2.3.1 气泡面积气泡的面积为气泡的像素面积,也就是气泡的投影连通域内像素点的个数。
2.3.2 当量直径气泡的直径定义为具有相同面积A的圆形的当量面积直径,简称当量直径,如式(1)所示:
| $ d = 2\sqrt {A/\pi } $ | (1) |
气泡尺寸的测量可能由于形状扭曲而变得复杂。在气泡足够小的情况下,由于气泡几乎是球形,所以气泡尺寸可以精确测量。但是,随着气泡尺寸的增加,形状从球形过渡到椭圆形。为了评估椭圆形气泡的大小,假定了一个理想的椭圆形形状,其较小(垂直)轴是对称轴[10]。计算这些气泡的形状涉及纵横比(E)的概念,如式(2)所示:
| $ E = h/w $ | (2) |
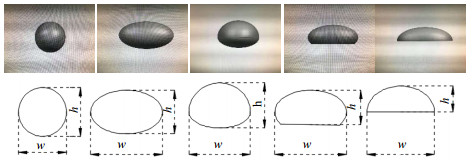
其中,w和h是气泡的水平和垂直直径。图 2所示为投影到垂直于摄像机获取视频的方向的平面上气泡的典型形状图像。图示说明松节油和松脂溶液中具有不同形状的气泡的纵横比的计算方法。
|
图 2 气泡的典型形状图 Fig.2 Images of typical bubble shapes |
松节油溶液中不同当量直径的气泡形状变化如图 3所示。由图 3可以看出,当气泡足够小时,气泡几乎为球形。随着气泡直径的增大,气泡形状从球形变化为椭球形,气泡直径较大时,气泡形状为球帽性。在松节油溶液中,由于黏性力较小,较大气泡表面有轻微的振荡形变。

|
图 3 松节油中不同当量直径气泡的形状变化 Fig.3 Bubbles with different equivalent diameters in turpentine (a) d = 0.5663 mm (b) d = 0.6016 mm (c) d = 1.0881 mm (d) d = 2.4669 mm (e) d = 2.974 mm (f) d = 3.338 mm |
不同溶液中的同一单气泡在上升过程中每经过0.02 s的形状特征如图 4所示。由图 4 (a)~(c)可见,松节油和S1、S2中,气泡在上升运动过程中都经历了一定程度竖直方向的振荡形变。图 4(a)中,松节油中气泡在上升过程中,气泡形状在竖直和水平两个方向均表现出强烈的振荡现象,发生不规则形状变化。图 4(d)~(e)中,气泡形变体现出一定规律性,形成椭球形气泡。对比不同溶液中气泡的形状特征,低黏度的流体中,较大气泡表现出轻微的振荡形变现象,具有不规律变化的形状特征,因此气泡的纵横比也会随之变化。

|
图 4 上升过程中气泡形状变化 Fig.4 Profiles of bubble shapes during rising (a) turpentine, d = 3.022 mm (b) S1, d = 2.6032 mm (c) S2, d = 3.1071 mm (d) S3, d = 2.7054 mm (e) S4, d = 2.488 mm |
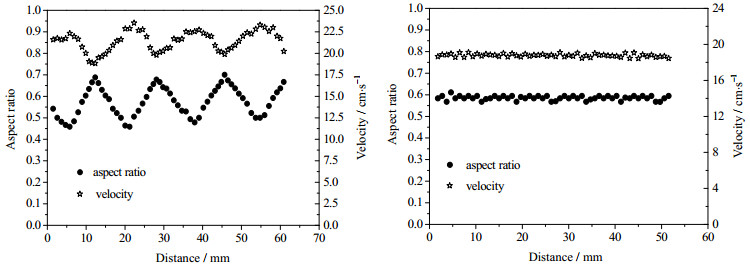
气泡纵横比随上升高度的关系如图 5所示。由图 5(a)可见,气泡纵横比随上升高度也表现出一定程度的波动。当流体黏度增大后,气泡形变体现出一定的规律性,气泡纵横比表现出一定的线性变化特征,得到规则的椭球形气泡。在松节油溶液中,直径2.3378 mm的气泡上升运动纵横比和速度都变现出规律的振荡,且纵横比和速度的变化趋势相反,即纵横比的波峰对应速度曲线的波谷。在黏度较大的S4溶液中,气泡形状为规则的椭球形气泡,其纵横比和速度曲线都呈稳定状态。
|
图 5 气泡纵横比和速度与上升高度的关系 Fig.5 Profiles of bubble aspect ratio and velocity as a function of rising distance (a) turpentine, d = 2.3378 mm (b) S4, d = 3.212 mm |
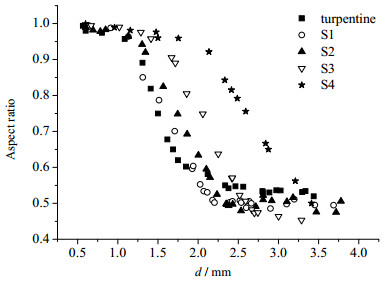
不同溶液中气泡纵横比E与气泡直径d的关系如图 6所示。由图 6可见,当d < 1 mm,纵横比基本保持为1,气泡为球形。当d > 1 mm,纵横比随着气泡直径的增大而减小,不同溶液的递减速度随黏度增大而减小。松节油溶液中纵横比变化速率较快,随着黏度的增大,纵横比随直径的变化速率减小,S4溶液中气泡纵横比对比于其他黏度较小的溶液,变化速率最慢。当气泡直径较大时,气泡的纵横比基本稳定,气泡的形状稳定。
|
图 6 不同溶液中气泡纵横比和直径的关系 Fig.6 Bubble aspect ratio as a function of bubble diameter in different solutions |
气泡在液体中运动时,其形状主要受浮力、表面张力、黏性力、惯性力的作用,因此,可以用奥特沃斯数(Eo)、韦伯数(We)、雷诺数(Re)等无量纲参数对气泡的形状进行描述[11-13],其中,Eo (Eo = gd2(ρl-ρg)/σ)是重力和表面张力的比值,表征重力和液体表面张力对气泡动力学特性的的影响;We (We = ρlVT2d/σ)是惯性力和表面张力的比值,表征惯性力和表面张力的影响;Re (Re = ρlVTd/μ)是惯性力和黏性力的比值,表征惯性力和黏性力的影响。
关于气泡纵横比的预测已有文献进行了实验研究或数值模拟研究,Wellek等[14]通过实验研究,提出了污染液体中非振荡液滴形变的预测模型,如式(3)所示:
| $ E = \frac{1}{{1 + 0.163E{o^{0.757}}}} $ | (3) |
Okawa[10]等对式(3)进行了修正,提出模型,如式(4)所示:
| $ E = \frac{1}{{1 + 1.97E{o^{1.3}}}} $ | (4) |
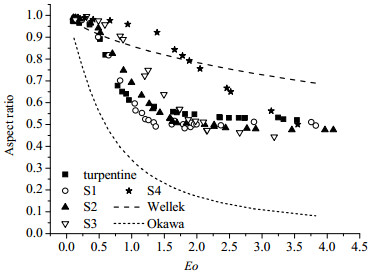
不同黏度溶液中气泡纵横比E与Eo的关系如图 7所示。由图 7可见,当Eo < 0.4,纵横比基本保持为1。当Eo > 0.4后,纵横比随着Eo的增大而减小,总体上出现分叉,呈现几条趋势线,黏度越小,趋势线越相近。黏度较大的S4溶液对比于其他黏度较小的溶液的纵横比变化趋势差别较大。从图 7中还可看出,Wellek等的经验公式与数据的上边界较吻合,除此之外,在整个实验范围内偏差较大。由于实验中采用了五种黏度不同的溶液,溶液中的黏度差别较大,由于Eo表征重力和表面张力的比值,不包含黏度项,Eo不适合用来描述松节油松脂溶液中气泡的变形。
|
图 7 不同溶液中纵横比与Eo的关系 Fig.7 Bubble aspect ratio as a function of Eo in different solutions |
另有一些文献引入了We数,得出了纵横比和We数之间的关系式。Moore[15]基于整个气泡表面周围的流动是非黏性的假设,提出了计算模型如式(5)所示。
| $ E = \frac{1}{{1 + 9We/64}} $ | (5) |
Taylor & Acrivos[16]对爬流中气泡的纵横比进行了研究,得到模型如式(6)所示。
| $ E = \frac{1}{{1 + 5We/32}} $ | (6) |
Wellek[14]等对严重污染液体中的非振荡液滴的形变进行了实验研究,提出了模型如式(7)所示。
| $ E = \frac{1}{{1 + 0.091W{e^{0.95}}}} $ | (7) |
Kelbaliyev等[17]提出了基于Re和We的纵横比预测模型,如式(8)所示。
| $ E = \frac{{1 - {\lambda _v}We}}{{1 + \frac{{{\lambda _v}}}{2}We}} $ | (8) |
其中,
Raymond等[18]指出当气泡不是椭球形时就不具备对称性。对于气泡尺寸较大形变严重的气泡,纵横比的值可用式(9)计算。
| $ E = 1 - \frac{{We}}{9} $ | (9) |
不同溶液中纵横比E与We的关系以及对比实验数据和Moore、Taylor & Acrivos、Wellek、Kelbaliyev和Raymond等提出的纵横比预测模型预测趋势线如图 8所示。由图 8可见,不同黏度的溶液中气泡的纵横比随We的变化趋势在实验范围内大致相同。对比几组预测模型,Wellek模型在较小We值时较吻合,We增大后与实验值偏离较大。当We < 2.2时,Moore、Taylor & Acrivos、Kelbaliyev和Raymond模型与实验值吻合良好,当We > 2.2时,4组模型的预测值都比实验值高。总体来说,Kelbaliyev和Raymond的预测模型较其他模型预测准确性更高。和Eo数相比,在整个气泡直径的实验范围内,不同黏度体系中相同直径气泡的We数差别较小,因此We数更适合关联松脂溶液中气泡形状大小。

|
图 8 不同溶液中纵横比与We的关系 Fig.8 Bubble aspect ratio as a function of We in different solutions |
Tadaki & Maeda[19]推导了一个新的无量纲参数Ta (Ta = ReMo0.23)通过大量实验数据,发现对于所测试的液体(Mo < 2.5 ×10-4),气泡纵横比能与Ta进行很好的关联,关联式如式(10)所示:
| $ {E^{1/3}} = \left\{ \begin{array}{l} \;\;\;\;\;\;1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Ta<2\\ 1.14T{a^{ - 0.176}}\;\;\;\;\;\;\;\;2<Ta<6\\ 1.36T{a^{ - 0.28}}\;\;\;\;\;\;\;\;6<Ta<16.5\\ \;\;\;\;0.62\;\;\;\;\;\;\;\;\;\;\;\;\;\;16.5<Ta \end{array} \right. $ | (10) |
Vakhrushev & Efremov[20]对上式进行了修正,通过数据拟合结果如式(11)所示:
| $ E = \left\{ {\begin{array}{*{20}{c}} 1&{Ta < 0.3}\\ {{{\left\{ {0.77 + 0.24\tanh \left[ {1.9\left( {0.4 - {{\log }_{10}}Ta} \right)} \right]} \right\}}^2}}&{0.3 < Ta < 20}\\ {0.3}&{20 < Ta} \end{array}} \right. $ | (11) |
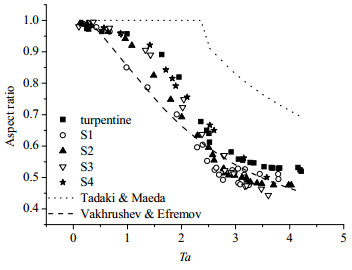
不同溶液中气泡纵横比E与Ta的关系以及Tadaki & Maeda和Vakhrushev & Efremov等提出的关于E和Ta的经验关联式预测结果如图 9所示。由图 9可见,Ta较小时,模型预测值与实验值上边界吻合,当Ta较大时,Tadaki & Maeda模型预测值较所有实验数据都偏高。Vakhrushev & Efremov经验关联式与实验数据的趋势发展相似性不大。
|
图 9 不同溶液中纵横比与Ta的关系 Fig.9 Bubble aspect ratio as a function of Ta in different solutions |
从图 7、8、9可以看出,随着无量纲数(Eo、We和Ta)的增大,纵横比总体上呈现减小的趋势,纵横比与无量纲数是反函数关系。综上所述,在本实验中用于描述松节油和松脂溶液中气泡形状的最佳无量纲参数为We数。采用We作为无量纲数,以实验数据为基础,运用最小二乘法进行拟合,提出新的预测模型如式(12)所示:
| $ E = \frac{1}{{1 + 0.103W{e^{1.723}}}} $ | (12) |
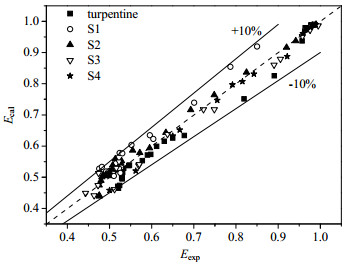
实验值与模型式(12)预测值的比较如图 10所示。由图 10比较可知,大部分数据在±10%的相对误差范围内一致,因而纵横比的预测值与实验值吻合良好。
|
图 10 纵横比的实验值与预测值的比较 Fig.10 Comparison of experimental and calculated aspect ratio results |
(1) 气泡直径d < 1 mm时,气泡保持为球形;当d > 1 mm时,气泡为椭球体或类似球帽的不规则形状。
(2) 黏度低的溶液中,较大气泡表面伴随有振荡,纵横比也随上升高度呈现波动变化。随着黏度增加,气泡纵横比几乎不变,气泡呈规则的椭球形。
(3) 提出了不同黏度体系中当量直径在0.5~4.0 mm的气泡纵横比预测模型,预测值与实验值的误差在±10%以内,拟合结果较好。
符号说明:
| A | —气泡面积,mm2 | w | —气泡的水平直径,mm |
| d | —气泡当量直径,mm | We | —韦伯数,We = ρlVT2d/σ,无量纲 |
| E | —纵横比,无量纲 | ρ | —密度,kg·m-3 |
| Eo | —奥特沃斯数,Eo=gd2(ρl-ρg)/σ,无量纲 | σ | —表面张力,N·m-1 |
| g | —重力加速度,m·s-2 | μ | —黏度,kg·s-2·m-1 |
| h | —气泡的垂直直径,mm | 下标 | |
| Mo | —莫顿数,Mo = (ρl-ρg)gμl4/σ3ρl2,无量纲 | cal | —计算值 |
| Re | —雷诺数,Re = ρlVTd/μl,无量纲 | exp | —实验值 |
| Ta | — Tadaki数,Ta = ReMo0.23,无量纲 | g | —气相 |
| VT | —气泡上升终速度,cm·s-1 | l | —液相 |
| [1] | Rodrigues-Corrêa K C D S, Lima J C D, Fett-Neto A G. Pine oleoresin:tapping green chemicals, biofuels, food protection, and carbon sequestration from multipurpose trees[J]. Food & Energy Security, 2012, 1(2): 81-93. |
| [2] | Zhang D, Zhou D, Wei X J, et al. Green catalytic conversion of hydrogenated rosin to glycerol esters using subcritical CO2 in water and the associated kinetics[J]. Journal of Supercritical Fluid, 2017, 125: 12-21. DOI:10.1016/j.supflu.2017.01.009. |
| [3] | Huang Y Y, Chen X P, Deng Y F, et al. A novel nickel catalyst derived from layered double hydroxides (LDHs) supported on fluid catalytic cracking catalyst residue (FC3R) for rosin hydrogenation[J]. Chemical Engineering Journal, 2015, 269: 434-443. DOI:10.1016/j.cej.2015.01.098. |
| [4] | Huang Y, Zhao S, Ding Y D, et al. Optimizing the gas distributor based on CO2 bubble dynamic behaviors to improve microalgal biomass production in an air-lift photo-bioreactor[J]. Bioresource Technology, 2017, 233: 84-91. DOI:10.1016/j.biortech.2017.02.071. |
| [5] | Yang Z B, Cheng J, Lin R C, et al. Improving microalgal growth with reduced diameters of aeration bubbles and enhanced mass transfer of solution in an oscillating flow field[J]. Bioresource Technology, 2016, 211: 429-434. DOI:10.1016/j.biortech.2016.03.127. |
| [6] | Rubio J, Smith R. Overview of flotation as a wastewater treatment technique[J]. Mineral Engineering, 2002, 15(3): 139-155. DOI:10.1016/S0892-6875(01)00216-3. |
| [7] | Parihar R, Upadhyay K. Production of bio-hydrogen gas from wastewater by anaerobic fermentation process:a review[J]. International Journal of Chemical Studies, 2015, 3(3): 07-14. |
| [8] | Kulkarni A, Joshi J. Bubble formation and bubble rise velocity in gas-liquid systems:a review[J]. Industrial & Engineering Chemistry Research, 2005, 44(16): 5873-5931. |
| [9] | HAO Zhi-gang(郝志刚), BAO Yu-yun(包雨云), GAO Zheng-ming(高正明). Gas-liquid dispersion in a multi-impeller stirred tank(多层组合桨搅拌槽内气-液分散特性的研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2004, 18(5): 547-552. DOI:10.3321/j.issn:1003-9015.2004.05.003. |
| [10] | Okawa T, Tanaka T, Kataoka I, et al. Temperature effect on single bubble rise characteristics in stagnant distilled water[J]. International of Heat and Mass Transfer, 2003, 46(5): 903-913. DOI:10.1016/S0017-9310(02)00345-9. |
| [11] | Clift R, Grace J R, Weber M E. Bubbles, drops, and particles[M].New York: Courier Dover Publications, 2005. |
| [12] | Bhaga D, Weber M E. Bubbles in viscous liquids:shapes, wakes and velocities[J]. Journal of Fluid Mechanics, 1981, 105(1): 61-85. |
| [13] | Grace J R. Shapes and velocities of bubbles rising in infinite liquids[J]. Transactions of the Institution of Chemical Engineers, 1973, 51(1): 116-120. |
| [14] | Wellek R M, Agrawal A K, Skelland A H P. Shape of liquid drops moving in liquid media[J]. AIChE Journal, 1996, 12(5): 854-862. |
| [15] | Moore D W. The rise of a gas bubble in a viscous liquid[J]. Journal of Fluid Mechanics, 1959, 6(1): 113-130. DOI:10.1017/S0022112059000520. |
| [16] | Taylor T D, Acrivos A. On the deformation and drag of a falling viscous drop at low Reynolds number[J]. Journal of Fluid Mechanics, 1964, 18(3): 466-476. DOI:10.1017/S0022112064000349. |
| [17] | Kelbaliyev G, Ceylan K. Development of new empirical equations for estimation of drag coefficient, shape deformation, and rising velocity of gas bubbles or liquid drops[J]. Chemical Engineering Communications, 2007, 194(12): 1623-1637. DOI:10.1080/00986440701446128. |
| [18] | Raymond F, Rosant J M. A numerical and experimental study of the terminal velocity and shape of bubbles in viscous liquids[J]. Chemical Engineering Science, 2000, 55(5): 943-955. DOI:10.1016/S0009-2509(99)00385-1. |
| [19] | Tadaki T, Maeda S. On the shape and velocity of single air bubbles rising in various liquids[J]. Kagaku Kogaku, 1961, 25(4): 254-264. DOI:10.1252/kakoronbunshu1953.25.254. |
| [20] | Vakhrushev I A, Efremov G I. A study of the hydrodynamics of a three-phase fluidized bed[J]. Chemistry and Technology of Fuels and Oils, 1969, 5(8): 541-545. DOI:10.1007/BF00727790. |




