换热网络是石油化工行业能源回收的重要组成部分,在高能耗的过程工业中对节约能源,提高能源效率具有重要意义[1]。根据工艺设计的换热网络往往不涉及旁路设计,因而存在控制自由度不足、控制性能难以提高等问题。另一方面,控制系统的设计也将影响过程系统的稳定性和最优性。稳定性是过程系统能够正常运行的首要条件,直接关系到产品的质量以及过程的安全性。蒋浩等[2]指出过程系统的稳定性是化工过程的一个基本特性,有必要研究系统的稳定程度。有研究者先后提出了将Routh-Hurwitz判据[3],矩阵测度[4]以及李雅普诺夫方程[5]用于稳定性的约束中,但这些方法只涉及系统的稳定性,并不涉及系统的稳定程度。WANG等[6-7]指出参数域上Hopf奇异点与操作点的距离越近,系统越容易进入不稳定区域。以上考虑稳定性约束的化工优化及稳定程度的定义都是在时域内进行的,但随着系统维数的增加,计算量将显著地增加,甚至很难求解[8]。在频域内研究系统稳定性的方法主要集中在理论研究,涉及奈奎斯特判据,且定义了单输入单输出系统的稳定裕度:幅值裕度和相角裕度[9]。但多变量系统的稳定裕度没有统一的定义。DOYLE等[10-12]提出一种多变量系统的稳定裕度计算方法,BRAATZ等[13]提出了一种不确定性系统的鲁棒性分析法,SAFONOV等[14]定义多变量系统的公共增益裕度,研究易于计算的下界对角扰动系统。WANG等[15-17]提出基于时域及频域分析法计算多变量系统相位稳定裕度的方法。LEHTOMAKI和MUKHOPADHYAY等[18-19]提出了回差阵奇异值法的概念,建立回差阵最小奇异值与传统增益裕度和相角裕度的关系。相较于时域内的Hopf奇异点,频域分析方法在工程运用中比较广泛且具有物理意义明确,计算简单的优点[20]。另一方面,换热网络的不确定性研究称为柔性分析,柔性是在不确定条件下保持长期稳定运行的能力。LIU等[21]总结了多年来柔性换热网络综合设计的成果及发展,柔性分析涉及非线性数学规划问题[22-23]。柔性换热网络综合则是设计满足一定柔性指标的换热网络[24-25]。白一媛等[26]总结了近年来结垢对柔性换热网络的影响。JIANG等[27]指出柔性区域内存在不稳定的部分,并提出考虑稳定性及柔性的换热网络设计方法。但是,以上方法侧重于稳态设计的角度不涉及过程系统的动态控制。考虑到过程系统的持续节能与优化,有必要通过旁路控制方法在达到良好控制性能的同时提高系统稳定性。WESTPHALEN等[28]提出一种定量衡量换热网络可控性的指标。罗雄麟等[29]通过逐一求解换热网络的非方相对增益矩阵(non square relative gain array,ns-RGA)确定最优的旁路位置。BRACCIA等[30-32]提出了一种兼顾柔性的多变量控制结构设计方法。近年来,预测控制[33]、模糊控制器[34]、自适应控制器[35]均被运用到换热网络中。但以上控制器的设计旨在提高控制性能并不涉及系统的稳定性。
针对以上的频域稳定裕度以及控制系统设计相关理论研究方法,提出一种基于频域稳定性分析的换热网络旁路控制方法。基于换热网络的动态模型,采用频域稳定性分析方法研究换热网络的稳定性,采用逆回差阵奇异值计算换热网络的稳定裕度;基于频域相对增益阵[36] (relative gain array,RGA),分析换热网络被控变量与操作变量之间的耦合关系,选择最优的潜在旁路;对优化的潜在换热网络旁路进行控制器的参数设计,使控制系统能够满足一定的稳定裕度要求,确定最终的设计方案,并对比不同方法设计的旁路控制效果。
2 换热网络频域稳定性分析换热网络由多个换热器组成,单个换热器的输出为下一个换热器的输入。本文中传递函数的输入输出为物流温度。假设换热网络有L个换热器,热流输入物流数为f,冷流输入物流数为h,则换热网络的传递函数如式(1)所示,
| $ \left[ {\begin{array}{*{20}{c}} {{y_1}}\\ {...}\\ {{y_f}}\\ {{y_{f + 1}}}\\ {...}\\ {{y_{f + h}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\prod\limits_{i = 1}^L {{G_{11, i}}} }&0&0&{{G_{12, i}}}&{...}&{{G_{{\rm{12}}, i}}}\\ 0&{...}&0&{...}&{..}&{...}\\ 0&0&{\prod\limits_{i = 1}^L {{G_{11, i}}} }&{{G_{12, i}}}&{..}&{{G_{12, i}}}\\ {{G_{21, i}}}&{...}&{{G_{21, i}}}&{\prod\limits_{i = 1}^L {{G_{22, i}}} }&0&0\\ {...}&{...}&{...}&0&{\prod\limits_{i = 1}^L {{G_{22, i}}} }&0\\ {{G_{21, i}}}&{...}&{{G_{21, i}}}&0&0&{\prod\limits_{i = 1}^L {{G_{22, i}}} } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_1}}\\ {...}\\ {{u_f}}\\ {{u_{f + 1}}}\\ {...}\\ {{u_{f + h}}} \end{array}} \right] $ | (1) |
式中,Gi表示第i个换热器的传递函数,单个换热器的传递函数模型为式(2) [37]。G11, i表示热流输入对热流输出的传递函数,若冷流与热流在第i个换热器中不换热则G11, i为1;G22, i表示冷流输入对冷流输出的传递函数,若冷流与热流在第i个换热器中不换热则G22, i为1;G12, i表示冷流输入对热流输出的传递函数,若冷流与热流在第i个换热器中不换热则G12, i为0;G21, i表示热流输入对冷流输出的传递函数,若冷流与热流在第i个换热器中不换热则G21, i为0。
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;\;\;\;\;{\kern 1pt} {\kern 1pt} \left[ \begin{array}{l} {y_1}\\ {y_2} \end{array} \right] = G(s)\left[ \begin{array}{l} {u_1}\\ {u_2} \end{array} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} G(s) = \left[ {\begin{array}{*{20}{c}} {\frac{{{a_1}{\rm{(}}{b_1}{\rm{ + }}s{\rm{ + }}A{b_2}{\rm{)}}}}{M}}&{\frac{{ - A{a_2}{b_1}}}{M}}\\ {\frac{{{a_1}{b_2}A}}{M}}&{\frac{{{b_1}{\rm{(}}{a_1}{\rm{ + }}s{\rm{ + }}A{a_2}{\rm{)}}}}{M}} \end{array}} \right]\\ M = {s^2} + ({a_1} + {b_1} + A{a_2} + A{b_2})s + A{a_1}{b_2} + A{a_2}{b_1} + 2{A^2}{a_2}{b_2} + {a_1}{b_1} \end{array} $ | (2) |
式中,a1、a2、b1、b2为系统参数,u1、y1为热流输入、输出,u2、y2为冷流输入、输出,A为换热器面积。
根据式(1),整个换热网络的传递函数行列式为,
| $ \det G(s) = \prod\limits_{i = 1}^L {{G_k}} $ | (3) |
式中Gk表示第k个换热器的传递函数的行列式,单个换热器传递函数的行列式如式(4),
| $ \det G(s) = \frac{{{a_1}{b_1}}}{{{s^2} + ({a_1} + {b_1} + A{a_2} + A{b_2})s + A{a_1}{b_2} + A{a_2}{b_1} + 2{A^2}{a_2}{b_2} + {a_1}{b_1}}} $ | (4) |
已知定理1 [9]:设s平面闭合曲线Г包围F(s)的Z个零点和P个极点,则s沿Г顺时针运动一周时,在F(s)平面上,F(s)闭合曲线ГF包围原点的圈数R = P -Z。
闭合曲线Г选择为奈奎斯特曲线,则可得到开环系统稳定时的条件,
| $ P=R+Z=0 $ | (5) |
式中P为开环系统的极点数,Z为开环系统的右半平面的零点数,R为奈奎斯特曲线包围原点的圈数。P等于0,即开环传递函数右半平面零点数与奈奎斯特曲线逆时针包围原点数相等,则开环系统稳定。
稳定裕度是定量表示系统稳定性的指标,多变量控制系统的稳定裕度还没有统一的定义。回差阵奇异值法由于只计算频率范围内的最小奇异值,计算量小,运用广泛。本文基于文献[38]提出的逆回差阵奇异值法计算换热网络的稳定裕度。
| $ \begin{array}{*{35}{l}} \text{GM}=20\text{lg}(1+m) \\ \text{PM}=2\text{arcsin}\frac{m}{2} \\ \end{array} $ | (6) |
其中,m为换热网络逆回差阵最小奇异值,PM为换热网络的相角裕度,GM为换热网络的幅值裕度。
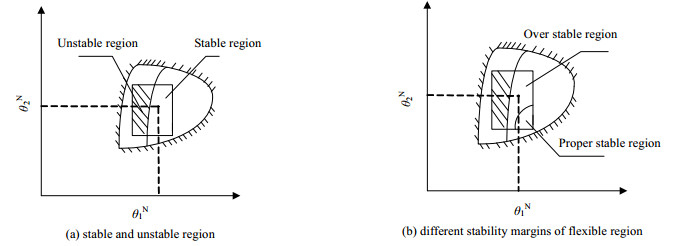
针对换热网络的不确定性,柔性设计被普遍采用,但不涉及过程系统的动态特性。文献[27]指出柔性的换热网络存在稳定和不稳定区域,如图 1(a)所示。考虑到过程系统动态特性,可以将换热网络柔性区域分为不稳定区域,合适的稳定区域和过稳定区域,如图 1(b)所示。在过稳定区域,系统的稳定裕度大,虽然抗干扰能力增加,但系统的响应越慢,超调增大,合适的稳定区域内虽然稳定裕度降低,但系统响应较快,超调较小。
|
图 1 柔性区域内的稳定性 Fig.1 Stability of flexible region |
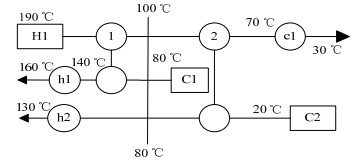
以文献[39]中简单换热网络为例,分析不同稳态点时换热网络的稳定裕度。换热网络包括了1股热流,2股冷流。其基本物流数据如表 1,换热网络结构如图 2。
|
|
表 1 基本物流数据 Table 1 Basic stream parameters |
|
图 2 换热网络结构图 Fig.2 The structure of HENs (heat exchanger networks) |
标称点换热器1的面积为1 258.71 m2,换热器2的面积为428.57m2。
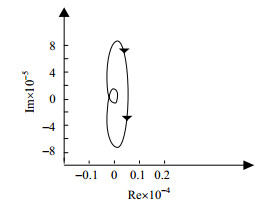
先判断系统的稳定性,由式(4)得到换热网络的行列式,则换热网络的奈奎斯特曲线如图 3所示,
|
图 3 换热网络奈奎斯特曲线 Fig.3 Nyquist curve of HENs |
由图 3可得,开环传递函数奈奎斯特曲线逆时针包围原点的个数为0,右半平面零点数为0,换热网络开环稳定。
为了系统有较好的动态特性,控制系统的幅值裕度一般取Am = [3, 6],相角裕度取φm = [30°, 60°],此时系统的控制性和鲁棒性较好[9]。
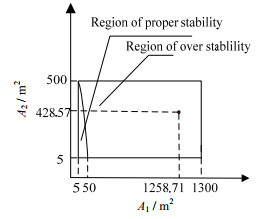
图 4中,横坐标为换热器1的面积,纵坐标为换热器2的面积。当换热器1面积小于50 m2,换热器2面积小于500 m2时,逆回差阵奇异值接近1。此时,换热网络的幅值裕度为6 db,相角裕度为60°,为稳定区域。当换热器面积再增加时,逆回差矩阵奇异值大于1,换热网络的稳定裕度不在最佳取值区间,为过稳定区域。因此应加入控制器改善系统的稳定裕度。通过以上分析得出,考虑稳定性的过程系统动态性能分析时应保证系统在合适的稳定区域,过稳定和不稳定都不利于系统运行和安全。
|
图 4 柔性区域内稳定裕度 Fig.4 Stability margins of flexible region |
基于相关增益阵(RGA)方法的控制系统设计在换热网络中已经广泛地运用,RGA是时域内分析系统耦合关系的方法。通过求取非方相关增益阵,选择值接近1的旁路进行配对。时域分析法的内在缺陷使基于RGA方法的控制系统设计不涉及系统的稳定性。在考虑到过程系统合适稳定区域分析的基础上,基于频域相对增益矩阵分析系统的耦合关系,在控制系统设计中加入稳定裕度的约束条件,使系统满足稳定裕度的要求。
设换热网络有q个被控目标,其中冷流数为qc,热流数为qh,n个潜在旁路,则换热网络的传递G(s)为q×n的矩阵,将s替换为jω,G(s)为G(jω),则换热网络频域相对增益阵为,
| $ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\left( \omega \right) = \mathit{\boldsymbol{G}}\left( {j\omega } \right) \otimes {\left[ {{\mathit{\boldsymbol{G}}^\varphi }\left( {j\omega } \right)} \right]^{\rm{T}}} $ | (7) |
其中⊗为两个矩阵的舒尔乘积,矩阵Gϕ(jω)为G(jω)的伪逆矩阵。Λ(ω)中的元素Λip表示第p个潜在旁路对第i个输出的频域相对增益值,Λip元素值与(1, 0j)点越接近,此条旁路耦合程度小。
式(7)中每个元素都为复数,无法比较各潜在旁路对被控变量的影响。文献[36]提出了耦合衡量系数和复平面单位圆图示分析法。
复数元素Λip(ω)为a(ω)+b(ω)j,与(1, 0j)的距离可表示为,
| $ {\lambda _{{\rm{ip}}}}(\omega ) = \sqrt {{{(a - 1)}^2} + {b^2}} $ | (8) |
将λip(ω)对频率ω取积分均值,可以得到
| $ {D_{{\rm{ip}}}} = \frac{1}{{{\omega _n} - {\omega _0}}}\int_{{\omega _0}}^{{\omega _n}} {{\lambda _{{\rm{ip}}}}(\omega ){\rm{d}}\omega } $ | (9) |
则Dip定义为耦合衡量系数。
Λ(ω)为频率ω的函数,将Λ(ω)对频率ω取积分均值,可以得到平均频域动态RGA。
| $ {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_0} = \frac{1}{{{\omega _n} - {\omega _0}}}\int_{{\omega _0}}^{{\omega _n}} {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}(\omega ){\rm{d}}\omega } $ | (10) |
本文中积分下限ω0的取值为0,积分上限ωn为带宽。
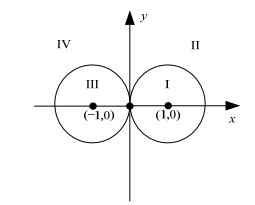
将复平面分为4个区域,如图 5所示。
|
图 5 频域相对增益区域的划分 Fig.5 Division of the relative frequency gain |
图 5中横坐标表示平均动态相对增益阵的实部,纵坐标表示平均动态相对增益阵的虚部,区域I表示圆心为(1, 0j)的单位圆,区域III表示圆心为(-1, 0j)的单位圆。当平均频域动态RGA的值在I区域中时,表示耦合程度低。在配对过程中,应该选择元素值为正,且接近点(1, 0j)的变量进行配对,同时不要选择元素值为负的变量配对,即III、IV区域中的旁路应当避免。
基于复平面单位圆图示分析法和耦合衡量系数法,得出了换热网络控制结构设计的配对原则:
(1) 去除耦合衡量系数矩阵中元素为1,或者接近1的潜在旁路;
(2) 在复平面单位圆中画出剩余的旁路,去除第III、IV区域中的旁路;
(3) 选择剩余旁路中离(1, 0j)点最近的点。
3.2 控制器参数设计频域相对增益阵只分析了潜在的旁路与被控变量的控制结构设计,并没有涉及控制器参数的设计,由稳定性及稳定裕度分析可知,基于柔性设计的换热网络稳定性过高,不满足系统的动态特性。因此,基于频域相对增益阵得到的潜在旁路,还应当进一步设计控制器,使换热网络满足一定的稳定性。
本文中换热网络为二阶系统,则频率特性为:
| $ \mathit{\boldsymbol{G}}(j\omega ) = \frac{{d + c\omega j}}{{\mathit{b}{\rm{ - }}{\omega ^2} + ja\omega }} $ | (11) |
控制器为PI控制器,控制器的频率特性为:
| $ {\mathit{\boldsymbol{G}}_c}(j\omega ) = {K_{\rm{P}}} - \frac{{{K_I}}}{\omega }j $ | (12) |
| $ \mathit{\boldsymbol{G}}(j\omega ){\mathit{\boldsymbol{G}}_{\rm{c}}}(j\omega ) = \frac{{d + c\omega j}}{{({\rm{b - }}{\omega ^2} + ja\omega )}}({K_{\rm{p}}} - \frac{{KI}}{\omega }j) $ | (13) |
PI控制器参数KP、KI为非负数。假设系统开环时的幅值裕度和相角裕度分别为Am和φm,系统的穿越频率和截止频率分别为ωx和ωc,可得到。
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{\rm{P}}} = - \frac{{(bd - d{\omega _x}^2 + ac{\omega _x}^2)}}{{{A_m}({c^2}{\omega _x}^2 + {d^2})}}}\\ {{K_{\rm{I}}} = \frac{{{\omega _x}(c{\omega _x}^3 + ad{\omega _x} - bc{\omega _x})}}{{{A_m}({c^2}{\omega _x}^2 + {d^2})}}} \end{array}} \right. $ | (14) |
| $ \begin{array}{l} \;\;\;{K_{\rm{P}}} = \frac{{{\omega _c}{\rm{sin}}({\phi _{\rm{m}}})(ad - bc + c{\omega _{\rm{c}}}^2)}}{{{c^2}{\omega ^2} + {d^2}}} - \frac{{{\rm{cos}}({\phi _{\rm{m}}})(bd - d{\omega _{\rm{c}}}^2 + ac{\omega _{\rm{c}}}^2)}}{{{c^2}{\omega ^2} + {d^2}}}\\ {K_{\rm{I}}} = \frac{{{\omega _{\rm{c}}}{\rm{sin}}({\phi _{\rm{m}}})(bd - d{\omega _{\rm{c}}}^2 + ac{\omega _{\rm{c}}}^2)}}{{{c^2}{\omega _{\rm{c}}}^2 + {d^2}}} + \frac{{{\omega _{\rm{c}}}{\rm{cos}}({\phi _{\rm{m}}})(ad{\omega _{\rm{c}}} - bc{\omega _{\rm{c}}} + c{\omega _{\rm{c}}}^3)}}{{{c^2}{\omega _{\rm{c}}}^2 + {d^2}}} \end{array} $ | (15) |
因此,由式(14)以及幅频特性Am的范围可确定一个KP、KI参数区域,由式(15)以及相频特性φm的范围可确定一个KP、KI参数区域,两个区域相互重叠的地方即为稳定裕度所要求的PI控制器参数区域。
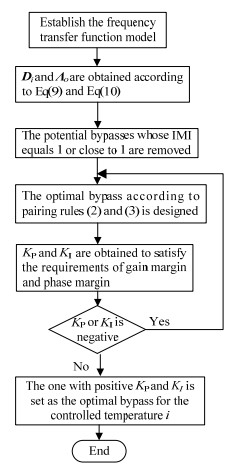
只有满足稳定性要求的潜在旁路才能是成功的配对结果,图 6为基于频域稳定性分析的换热网络控制结构设计方法。
|
图 6 换热网络控制系统设计过程 Fig.6 Flow chart of the design of HENs control system design |
图 6中的策略是基于频域配对原则及满足稳定裕度要求的换热网络控制系统设计方法。首先,根据频域相对增益阵计算出换热网络的耦合系数矩阵,去除元素为1的潜在旁路,依据频域相对增益阵计算出平均频域动态RGA,在复平面上表示出余下的潜在旁路,选择接近(1, 0j)点的旁路为最优旁路,再对旁路设计控制器参数,使控制系统的稳定裕度在合适的区间,若没有出现负数,则为最优旁路,若出现负数,则在复平面上重新选择潜在旁路。
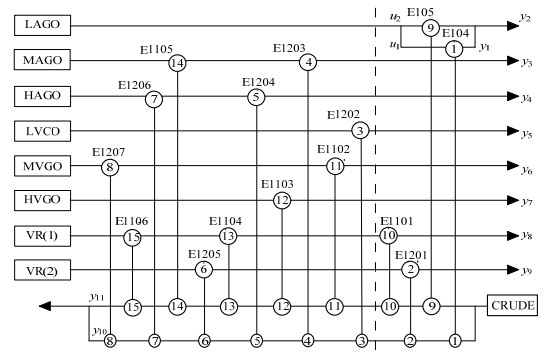
4 示例分析以某常减压蒸馏装置脱盐前换热网络为例[40],换热网络结构如图 7所示,原油换热网络包括9个物流输入,9个物流输出,15个换热器,该换热网络的物流数据见表 2。
|
图 7 原油换热网络结构图 Fig.7 Structure of the crude oil heat exchanger network |
|
|
表 2 原油换热网络基本物流数据 Table 2 Basic stream parameters of crude oil heat exchanger |
由文献[29]中对复杂换热网络的分析可知,旁路的设置一般在冷流。则此原油换热网络有潜在旁路15个,控制目标为原油以及LVCO的输出温度。
4.1 控制结构设计y5为换热网络中减一中的出口温度,原油在入口处分流,分为两股,则输出温度分别表示为y10和y11。由式(1)中的动态模型,y5、y10和y11的耦合衡量系数如表 3所示。
|
|
表 3 被控变量的耦合衡量系数 Table 3 Interaction measurement indices of controlled variables |
依据配对原则,去除耦合衡量系数为1或者接近1的潜在旁路,则输出y5的潜在旁路位置为E104、E1105、E1201、E1202,输出y10的潜在旁路位置为E1205、E1206、E1207,输出y11的潜在旁路位置为E1103、E1104、E1105、E1106。依据动态模型,计算出平均频域动态RGA,则表 3可以简化为表 4。
|
|
表 4 简化的潜在旁路 Table 4 Simplified potential bypasses |
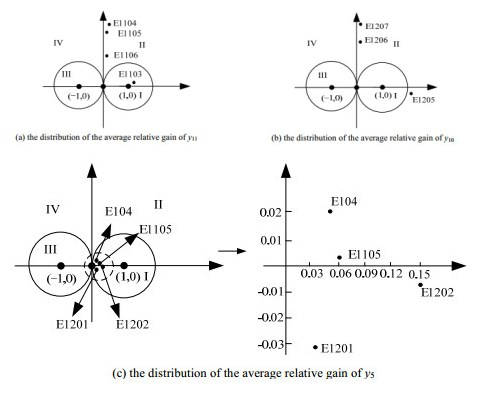
将表 4中简化潜在旁路的平均频域动态RGA在复平面上表示为如图 8,
|
图 8 系统平均频域相对增益的分布 Fig.8 Distribution of the average relative gain in frequency domain |
由图 8(a)可知,潜在旁路E104、E1105、E1201、E1202的平均频域相对增益都在第I区域,此时,比较四个平均频域相对增益的位置,E1202离点(1, 0j)的位置更近,则旁路的位置应设计在换热器E1202的冷流旁。
由图 8(b)可知,潜在旁路E1205、E1206、E1207的平均频域相对增益都在第II区域,此时,比较3个平均频域相对增益的位置,E1205离点(1, 0j)的位置更近,则旁路的位置应设计在换热器1205的冷流旁。由图 8(c)可知,潜在旁路E1104、E1105、E1106的平均频域相对增益都在第II区域,而E1103在第I区域,比较4个平均频域相对增益的位置,E1103离点(1, 0j)的位置更近,则旁路的位置应设计在换热器E1103的冷流旁。
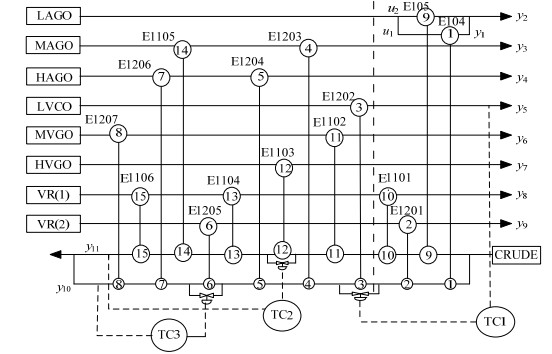
最优的旁路位置为E1202、E1205、E1103,换热网络的控制结构如图 9所示,
|
图 9 具有旁路控制的实际换热网络 Fig.9 Practical heat exchanger networks with bypass control |
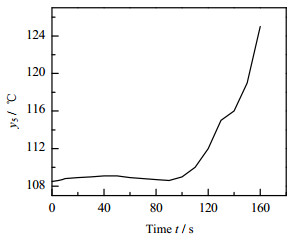
依据本文的配对结果,基于常规PID参数调节,在控制器TC1中手动设置PI参数,P为4,I为0.12,则物流y5的输出为如图 10所示,
|
图 10 y5的输出温度 Fig.10 Outlet temperature profile of y5 |
图 10中,输出温度y5的响应较快,但在120 s时,系统出现不可控的状态,系统输出不稳定。系统在调节PI参数时,应当避免出现不稳定的状态。因此,控制系统参数设计中有必要考虑过程系统的稳定。
采用本文提出的方法,依据式(14)与(15),对优化的旁路控制器设计PI参数,其参数设计及稳定裕度如表 5。
|
|
表 5 PI参数及稳定裕度 Table 5 PI parameters and stability margins |
基于表 5中的相角裕度和幅值裕度表明本文设计的控制系统满足频域稳定性要求,系统稳定。在此基础上,通过动态仿真对比分析文献[41]与本文提出方法的动态仿真结果。在文献[41]中不涉及对稳定性的分析与计算,同时通过在线优化设置PI控制器参数。分别对本文提出的控制系统和文献中的控制系统求解阶跃响应仿真结果,此时原油输入温度由55.1改变为56 ℃,PI控制器参数,稳定裕度及绝对误差积分(IAE)如表 6所示。
|
|
表 6 不同文献控制对比 Table 6 Comparison of control from different references |
绝对误差积分(IAE)作为控制性能评价函数,能定量反映控制系统的控制效果,控制效果越好,IAE的数值越小。文献[41]中设计的PI参数使系统的稳定裕度增大,系统的抗干扰能力强,但系统的IAE也增大,控制效果则不如本文基于频域稳定性分析方法设计的控制器。
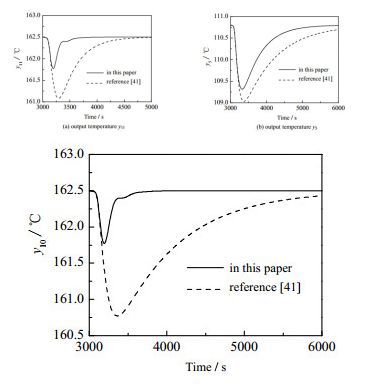
已知输出温度y5、y10与y11的给定值为110、162及162 ℃,当原油入口温度为52 ℃时,在本文及文献[41]优化的旁路位置及控制器作用下原油及减一中输出温度的阶跃响应曲线如图 11(a)、11(b)和11(c)所示。
|
图 11 输出温度对比 Fig.11 Comparison of the outlet temperatures |
图 11中,实线为在本文优化的旁路位置及控制器参数的条件下,原油及减一中的输出温度,虚线为在文献[41]优化的旁路及在线优化控制器参数的控制作用下,原油及减一中的输出温度。从图 11中可以得出,本文优化的方法的控制作用下y11上升时间为168.34 s,余差为0.004 ℃,而对比文献[41]方法的上升时间为228.86 s,余差为0.013 ℃;y5上升时间为252.02 s,余差为0.014 ℃,而对比文献[41]方法的上升时间为244.41 s,余差为0.113 ℃;y10上升时间为165.32 s,余差为0.003 ℃,而对比文献[41]方法的上升时间为280.26 s,余差为0.067 ℃。可见本文提出的设计方法有着较快的响应速度和较小的余差,控制性能比文献[41]的要好。由表 6和图 11可知,本文结合频域稳定性分析和求解方法,提出的基于频域稳定性分析的换热网络旁路控制系统在满足控制和操作要求的同时,考虑了系统的稳定性并提高了系统的控制性能。
5 结论换热网络的旁路控制可以保证系统的持续节能,基于频域稳定性分析方法,通过频域稳定性分析和对稳定裕度的定量求解,提出一种换热网络旁路控制方法。通过对比分析得出:
(1) 基于柔性设计的换热网络稳定性过高,系统的动态性能不佳,在控制系统旁路设计过程中,应考虑系统的稳定裕度。
(2) 基于频域相对增益阵提出了定量分析换热网络潜在旁路与被控变量之间耦合关系的方法,并基于复平面单位圆图示分析法和耦合衡量系数矩阵法,提出了换热网络的配对原则,选择最优的旁路位置。
(3) 针对优化的旁路位置,进行控制器的参数设计以满足一定的稳定裕度,确定最终的配对方案。通过分析对比可以得出其他文献优化的旁路位置会存在不满足频域设计指标的情况,导致系统的控制性能差,考虑频域稳定性设计方法不仅可以满足一定的稳定裕度要求,且控制效果更好,证明了本方法的优越性。
换热网络的旁路设计是换热网络控制的重要手段,旁路的设计过程中重点研究动态控制性能、稳定性以及经济性3者之间的关系,针对换热过程中的效率损失将在此基础上进行。
|
|
| [1] |
XIA L, FENG Y L, SUN X Y, et al. Design of heat exchanger network based on Entransy theory[J]. CIESC Journal, 2018, 26(8): 1692-1699. |
| [2] |
蒋浩, 陈丙珍. 化工过程稳定性分析研究进展[J]. 化工学报, 2018, 69(1): 76-87. JIANG H, CHEN B Z. Research progress of chemical process stability analysis[J]. CIESC Journal, 2018, 69(1): 76-87. |
| [3] |
HURWITZ A. On the conditions under which an equation has only roots with negative real parts[J]. Mathematische Annalen, 1895, 46(2): 273-284. DOI:10.1007/BF01446812 |
| [4] |
KOKOSSIS A, FLOUDAS C. Stability in optimal design:Synthesis of complex reactor networks[J]. AIChE Journal, 1994, 40(5): 849-861. DOI:10.1002/aic.690400511 |
| [5] |
BLABCO A M, BANDONI J A. Eigenvalue optimization-based formulations for nonlinear dynamics and control problems[J]. Chemical Engineering and Processing:Process Intensification, 2007, 46(11): 1192-1199. DOI:10.1016/j.cep.2006.04.014 |
| [6] |
WANG H Z, ZHANG N, QIU T, et al. Optimization of a continuous fermentation process producing 1, 3-propane diol with Hopf singularity and unstable operating points as constraints[J]. Chemical Engineering Science, 2014, 116(9): 668-681. |
| [7] |
WANG H Z, ZHANG N, QIU T, et al. A process design framework singularity points in chemical processes[J]. Chemical Engineering Science, 2013, 99(8): 252-264. |
| [8] |
聂卓赟.增益、相位裕度计算与控制器设计研究[D].长沙: 中南大学, 2012. NIE Z Y. The gain and phase margins calculation and controllers design[D]. Changsha: Central South University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10533-1012475009.htm |
| [9] |
胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2013. HU S S. Automatic control principle[M]. Beijing: Science Press, 2013. |
| [10] |
DOYLE J. Robustness of multiloop linear feedback systems[C]//1978 IEEE Conference on Decision and Control including the 17th Symposium on Adaptive Processes. New York: IEEE, 1979: 12-18. https://link.springer.com/article/10.1134/S1064230717030042
|
| [11] |
DOYLE J. Analysis of feedback systems with structured uncertainty[J]. IEE Proceedings. Part D:Control Theory and Applications, 1982, 129(6): 242-250. DOI:10.1049/ip-d.1982.0053 |
| [12] |
DOYLE J, WALL J E, STEIN G. Performance and robustness analysis for structured uncertainty[C]//1982 21st IEEE Conference on Decision and Control. Philadelphia: IEEE, 1982: 629-636. https://www.researchgate.net/publication/224681678_Performance_and_Robustness_Analysis_for_Structured_Uncertainties
|
| [13] |
BRAATZ R P, YOUNG P M, DOYLE J C, et al. Computational complexity of μ calculation[J]. Automatic Control IEEE Transactions on, 1994, 39(5): 1000-1002. DOI:10.1109/9.284879 |
| [14] |
SAFONOV M G. Stability margins of diagonally perturbed multivariable feedback systems[J]. IEE Proceedings. Part D:Control Theory and Applications, 1982, 129(6): 251-256. DOI:10.1049/ip-d.1982.0054 |
| [15] |
WANG Q G, LIN C, YE Z, et al. A quasi-LMI approach to computing stabilizing parameter ranges of multi-loop PID controllers[J]. Journal of Process Control, 2007, 17(1): 59-72. DOI:10.1016/j.jprocont.2006.08.006 |
| [16] |
WANG Q G, HE Y, YE Z, et al. On loop phase margins of multivariable control systems[J]. Journal of Process Control, 2008, 18(2): 202-211. DOI:10.1016/j.jprocont.2007.06.004 |
| [17] |
YE Z, WANG Q G, HANG C C. Frequency domain approach to computing loop phase margins of multivariable systems[J]. IFAC Proceedings Volumes, 2008, 41(2): 6131-6135. DOI:10.3182/20080706-5-KR-1001.01035 |
| [18] |
LEHTOMAKI N, SANDELL N J, ATHANS M. Robustness results in linear-quadratic Gaussian based multivariable control designs[J]. Automatic Control IEEE Transactions on, 1981, 26(1): 75-93. DOI:10.1109/TAC.1981.1102565 |
| [19] |
MUKHOPADHYAY V, NEWSOM J. Application of matrix singular value properties for evaluating gain and phase margins of multiloop systems[C]//AIAA Guidance Navigation and Control Conference. San Diego: AIAA, 1982: 420-428.
|
| [20] |
FREUDENBERG J S, LOOZE D P. Frequency domain properties of scalar and multivariable feedback systems[M]. New York: Springer, 1988.
|
| [21] |
KANG L X, LIU Y Z. Synthesis of flexible heat exchanger networks:A review[J]. CIESC Journal, 2018, 27(7): 1485-1497. |
| [22] |
SWANEY R E, GROSSMANN I E. An index for operational flexibility in chemical process design. Part Ⅱ:Computational algorithms[J]. AIChE Journal, 1985, 31(4): 631-641. DOI:10.1002/aic.690310413 |
| [23] |
SWANEY R E, GROSSMANN I E. An index for operational flexibility in chemical process design. Part I:Formulation and theory[J]. AIChE Journal, 1985, 31(4): 621-630. DOI:10.1002/aic.690310412 |
| [24] |
GROSSMANN I E, FLOUDAS C A. Active constraint strategy for flexibility analysis in chemical processes[J]. Computers & Chemical Engineering, 1987, 11(6): 675-693. |
| [25] |
GROSSMANN I E, FLOUDAS C A. Synthesis of flexible heat exchanger networks with uncertain flowrates and temperatures[J]. Computers & Chemical Engineering, 1987, 11(4): 319-336. |
| [26] |
白一媛, 刘琳琳, 顾偲雯, 等. 考虑污垢生长的柔性换热器网络综合[J]. 高校化学工程学报, 2018, 32(4): 926-932. BAI Y Y, LIU L L, GU S W, et al. Synthesis of flexible heat exchanger network with fouling growth[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(4): 926-932. DOI:10.3969/j.issn.1003-9015.2018.04.024 |
| [27] |
JIANG H, CHEN B Z, WANG H, et al. Novel method for considering process flexibility and stability simultaneously[J]. Industrial & Engineering Chemistry Research, 2014, 53(38): 14765-14775. |
| [28] |
WESTPHALEN D L, YOUNG B R, SVRCEK W Y. A controllability index for heat exchanger networks[J]. Industrial and Engineering Chemistry Research, 2003, 42(20): 4659-4667. DOI:10.1021/ie020893z |
| [29] |
罗雄麟, 白玉杰, 侯本权, 等. 基于相对增益分析的换热网络旁路设计[J]. 化工学报, 2011, 62(5): 1318-1325. LUO X L, BAI Y J, Hou B Q, et al. Optimal design of bypass location on heat exchanger networks based on relative gain array analysis[J]. CIESC Journal, 2011, 62(5): 1318-1325. DOI:10.3969/j.issn.0438-1157.2011.05.021 |
| [30] |
BRACCIA L, MARCHETTI P A, LUPPI P, et al. Multivariable control structure design based on mixed-integer quadratic programming[J]. Industrial and Engineering Chemistry Research, 2017, 56(39): 11228-11244. DOI:10.1021/acs.iecr.7b02270 |
| [31] |
BRACCIA L, MARCHETTI P A, LUPPI P, et al. Multivariable control structure design of heat exchange networks based on mixed-integer quadratic programming[J]. Computer Aided Chemical Engineering, 2018, 56(39): 11228-11244. |
| [32] |
BRACCIA L, MARCHETTI P A, LUPPI P, et al. A sequential integration between optimal flexible heat exchanger[J]. Industrial and Engineering Chemistry Research, 2018, 57(32): 11094-11111. DOI:10.1021/acs.iecr.8b01611 |
| [33] |
FRATCZAK M, CZECZOT J, NOWAK P, et al. Practical validation of the effective control of liquid-liquid heat exchangers by distributed parameter balance-based adaptive controller[J]. Applied Thermal Engineering, 2017, 129(1): 549-556. |
| [34] |
ORAVEC J, BAKOŠOV M, TRAFCZYNSKI M, et al. Robust model predictive control and PID control of shell-and-tube heat exchangers[J]. Energy, 2018, 159: 1-10. DOI:10.1016/j.energy.2018.06.106 |
| [35] |
VASIČKANINOV A, BAKOŠOV M. Control of a heat exchanger using neural network predictive controller combined with auxiliary fuzzy controller[J]. Applied Thermal Engineering, 2015, 89(10): 1046-1053. |
| [36] |
许锋, 潘琦, 王一岚, 等. 工业过程多变量系统常规控制结构的频域设计[J]. 清华大学学报(自然科学版), 2016, 56(4): 448-452. XU F, PAN Q, WANG Y L, et al. Frequency domain design method for decentralized control of multivariable processes[J]. Journal of Tsinghua University (Natural Science Edition), 2016, 56(4): 448-452. |
| [37] |
罗雄麟. 化工过程动态学[M]. 北京: 化学工业出版社, 2004. LUO X L. Chemical process dynamics[M]. Beijing: Chemical Industry Press, 2004. |
| [38] |
李信栋, 苟兴宇. 多输入多输出线性定常系统稳定裕度的分析与改进[J]. 控制理论与应用, 2014, 31(1): 105-111. LI X D, GOU X Y. Analysis and improvement of stability margin for multi-input multi-output linear time-invariant systems[J]. Control Theory and Applications, 2014, 31(1): 105-111. |
| [39] |
SUN L, LUO X. Synthesis of multipass heat exchanger networks based on pinch technology[J]. Computers and Chemical Engineering, 2011, 35(7): 1257-1264. DOI:10.1016/j.compchemeng.2010.08.005 |
| [40] |
SUN L, ZHA X L, LUO X L. Coordination between bypass control and economic optimization for heat exchanger network[J]. Energy, 2018, 160: 318-329. DOI:10.1016/j.energy.2018.07.021 |
| [41] |
罗雄麟, 孙琳, 王传芳, 等. 换热网络操作夹点分析与旁路优化控制[J]. 化工学报, 2008, 59(5): 1200-1206. LUO X L, SUN L, WANG C F, et al. Operating pinch point analysis and bypass optimal control of heat exchanger networks[J]. Journal of Chemical Industry and Enginering (China), 2008, 59(5): 1200-1206. DOI:10.3321/j.issn:0438-1157.2008.05.020 |




