基于特征空间自适应k近邻工业过程故障检测

引用本文

郭小萍, 徐月, 李元. 基于特征空间自适应k近邻工业过程故障检测[J]. 高校化学工程学报, 2019, 33(2): 453-461. DOI: 10.3969/j.issn.1003-9015.2019.02.025.

GUO Xiao-ping, XU Yue, LI Yuan. A feature space adaptive k-nearest neighbor method for industrial fault detection[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(2): 453-461. DOI: 10.3969/j.issn.1003-9015.2019.02.025.

基金项目

国家自然科学基金（61673279）；国家自然科学基金重大项目（61490701）；辽宁省科学事业公益研究基金（2016001006）。

通讯联系人

李元, E-mail:li-yuan@mail.tsinghua.edu.cn

作者简介

郭小萍(1972-), 女, 山西大同人, 沈阳化工大学副教授, 博士。

文章历史

收稿日期：2018-05-23;
修订日期：2018-09-04。

Contents Abstract Full text Figures/Tables PDF

基于特征空间自适应k近邻工业过程故障检测

郭小萍 , 徐月 , 李元

沈阳化工大学信息工程学院，辽宁沈阳 110142

收稿日期：2018-05-23；修订日期：2018-09-04。

基金项目：国家自然科学基金（61673279）；国家自然科学基金重大项目（61490701）；辽宁省科学事业公益研究基金（2016001006）。

作者简介：郭小萍(1972-), 女, 山西大同人, 沈阳化工大学副教授, 博士。

通讯联系人：李元, E-mail:li-yuan@mail.tsinghua.edu.cn

摘要：针对工业生产过程故障检测模型不能及时更新的问题，提出了一种特征空间自适应k近邻（feature space adaptive k-nearest neighbor，FS-AkNN）故障检测方法。首先利用主元分析对训练数据进行降维，构建特征空间，然后利用k最近邻方法建立故障检测模型。在过程监视过程中，提出了基于距离规则的自适应更新故障检测模型。通过一个数值例子和TE过程的仿真实验结果表明了该方法的有效性。

关键词：自适应 k近邻(kNN) 主元分析故障检测

A feature space adaptive k-nearest neighbor method for industrial fault detection

GUO Xiao-ping , XU Yue , LI Yuan

College of Information Engineering, Shenyang University of Chemical Technology, Shenyang 110142, China

Abstract: Failure models for production process usually cannot be updated in time. This study proposed a feature space adaptive k-nearest neighbor (FS-AkNN) fault detection method. Principal component analysis was used to reduce training data dimension and construct a feature space. A fault detection model was then established using a k-nearest neighbor method. Moreover, a distance-based rule adaptive update fault detection model was proposed for process monitoring. Simulation results of numerical example and the TE process showed the effectiveness of the method.

Key words: adaptive k-nearest neighbor (kNN) principal component analysis fault detection

1 前言

随着现代工业过程生产规模的不断扩大，企业生产系统的自动化水平和集成化程度不断提高，生产单元之间的高关联性使得过程故障具有了比以往更强的破坏性。为了减少故障造成的影响，基于数据驱动的故障检测方法受到了广泛关注^[1-2]。近年来，在解决具有非线性、多模态、自适应等方面特征的工业过程故障检测取得了很多成果，其中主元分析(principal component analysis，PCA)和k近邻方法(k-nearest neighbor，kNN)在故障检测方面得到了较多应用^[3-6]。

传统PCA方法建立故障检测模型时，假设被检测系统中的过程参数其统计特性在所在的时间尺度上保持不变，模型一旦建立则保持固定不变^[7]，这使其可能不适用于实际工业生产过程的过程监视。HE等提出的kNN方法适用于具有非线性特性的过程^[8]，但其建立的故障检测模型也是固定的。实际工业过程中由于装置的磨损、老化、工作环境的影响，实时数据可能包含建模数据忽略的过程信息。故障检测模型不能及时更新，容易导致误报现象。

为了解决模型更新的问题, LI等提出了递归主元分析(recursive principal component analysis，RPCA)^[9]，利用递归的方法在阈值内更新样本。该方法在更新模型时随着时间的增加数据规模越来越大，增加计算的复杂度。WOLD等在指数递归方法的基础上，提出了指数加权滑动PCA (exponentially weighted moving principal components analysis，EWMPCA)^[10]，但该方法毎次更新模型时更新的是整个历史数据库，这对实时更新模型造成了很大的阻力。基于递归方法LEE等提出了自适应多块PCA法(adaptive multiblock principal component analysis, adaptive MPCA)和自适应多尺度PCA法(adaptive multiscale principal component analysis)^[11-13]。这两种方法利用系统在线运行数据对诊断模型进行及时更新，从而提高故障诊断性能。但是，采用递归的方法更新模型时的计算量较大，可能影响模型的更新速度^{[7, 14]}。耿志强等人在基于一种阈值法的基础上提出了移动窗递推主元分析(moving window recursive principal component analysis, MWRPCA)，改进了移动窗主元分析(moving window principal component analysis, MWPCA)^[15-16]，但窗宽参数确定存在难度。

本文提出一种自适应k近邻方法，解决故障检测模型不能及时更新的问题。首先，利用主元分析方法对训练数据进行处理，构建特征空间，在保留原始训练样本尽可能多信息的同时大大降低数据维度，为下一步自适应k近邻的计算降低了复杂程度。然后，在特征空间中构建k近邻统计量。在监视过程中，首先寻找测试数据的近邻，然后使用基于距离的更新规则，更新原始训练数据，使模型能够自适应地更新。最后，通过一个数值例子和TE过程进行故障检测仿真实验，仿真结果表明该方法的有效性。

2 特征空间自适应kNN故障检测方法 2.1 特征空间构建

PCA是多元统计分析中最基本的投影模型之一。假设一个训练数据矩阵X∈R^m×n，其中m代表样本的数量，n代表变量的数量。首先对X按零均值，单位标准差进行标准化，则其协方差矩阵为：

$\mathit{\boldsymbol{S}} = {\mathop{\rm cov}} (\mathit{\boldsymbol{X}}) = \frac{1}{{m -1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} $

(1)

对其进行特征值分解，并按照特征值的大小降序排列。PCA模型对X进行如下分解：

$\mathit{\boldsymbol{X}} = \mathop X\limits^ \wedge +\mathit{\boldsymbol{E}} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{P}}^{\rm{T}}} +\mathit{\boldsymbol{E}} $

(2)

$\mathit{\boldsymbol{T}} = \mathit{\boldsymbol{XP}} = \left\{ {{T_{i,a}}} \right\},a = 1,2,...A;i = 1,2,...m $

(3)

$Q = \mathit{\boldsymbol{SPE}} = \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{E}}^{\rm{T}}}{\rm{ = }}\left\{ {{q_i}} \right\},i = 1,2,...m $

(4)

其中P∈R^n×A为负载矩阵，由S的前A个特征向量构成。T∈R^m×A为得分矩阵，T的各列被称为主元变量，A表示主元的个数，也是得分矩阵的列数。采用T和统计量Q构造特征空间X'^[17]：

$\mathit{\boldsymbol{X'}} = \left[ \mathit{\boldsymbol{T}} \right.\left. Q \right] $

(5)

2.2 k近邻故障检测方法及自适应更新规则

k近邻法建立故障检测模型时只采用正常样本数据。通过提取正常样本之间的最近邻，构造最近邻距离平方和，确定统计量的统计控制限D_lim ^[5]。通常来说，判断故障的准则是故障的数据与正常的数据表现出很小的相似性^[18]。就kNN规则而言是故障数据的k近邻距离平方和大于正常数据的k近邻距离平方和。在得到阈值后，更新过程所希望的样本是与训练样本具有很高的相似性，同时包含训练数据所没有的过程信息，为模型提供工业过程的最新信息。使用这些数据更新训练数据不仅能够使故障检测模型自动更新，同时降低了计算复杂度^[19]。为了实现这一目的，引入一个更新因子q(q∈(0, 1))定义需要更新的样本。计算测试样本的k(1 -q)个和k(1 +q)个近邻的距离平方和，记为D_k(1-q)和D_k(1+q)。

1) 当D_k_(1+q)≤ D_lim时，该样本为包含与训练数据相同信息的不必要更新样本。

2) 当D_k(1-q) < D_lim且D_k_(1+q) > D_lim时，该样本为包含过程最新信息的更新样本。

3) 当D_k(1-q) ≥ D_lim时，该样本为故障样本。

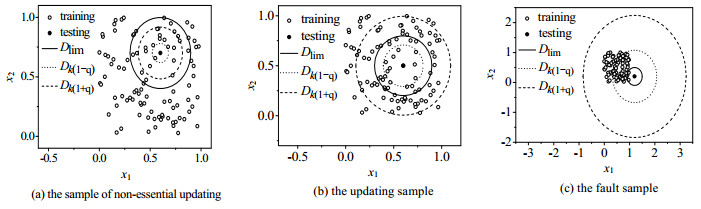
如图 1所示，(a)中样本的D_k(1+q)≤ D_lim，虽然与训练数据具有很高的相似性，但它所包含的信息与训练数据相同，所以该样本被视为不必要更新样本；(b)中样本的D_k(1-q) < D_lim且D_k(1+q) > D_lim，不仅与训练数据具有很高的相似性，同时包含新的信息，所以该样本被视为更新样本；(c)中所示样本的D_k(1-q)≥ D_lim，与训练数据具有极低的相似性，所以该样本被视为故障样本。其中k = 3，q = 0.2。

图 1 定义样本类型示意图 Fig.1 Schematic diagram of sample type definition

2.3 特征空间自适应kNN模型建立及过程监视

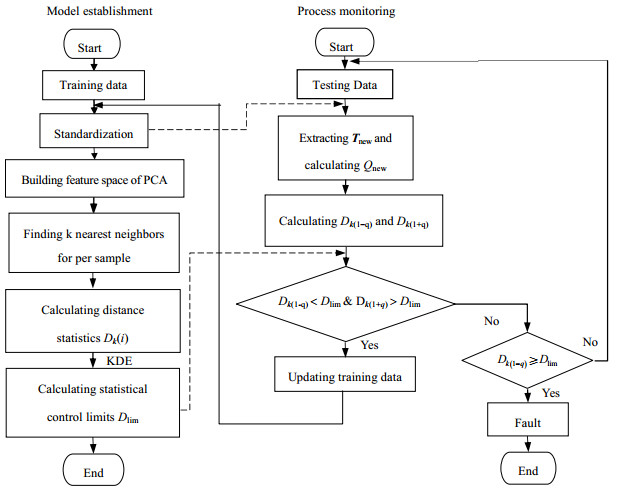
该方法主要流程图如图 2所示。

图 2 特征空间自适应kNN故障检测流程图 Fig.2 Flowchart of the feature space adaptive kNN fault detection process

2.3.1 模型建立

建立故障检测模型的步骤：

1) 在正常样本中选取训练数据X，并对训练数据按零均值，单位标准差进行标准化。

2) 采用PCA降维，构建特征空间X'。

a) 求标准化后的训练数据的协方差矩阵S。

b) 对协方差矩阵S进行特征值分解，提取主元T和计算统计量Q，构造特征空间X'。

3) 在X'中进行kNN计算。寻找每个样本的k个近邻，并计算k个近邻的距离平方和，获得正常状态下的故障检测统计量D_k(i), i = 1, 2, 3…, m。

4) 采用核密度估计法确定其置信度为95%的控制限，记为D_lim。

2.3.2 过程监视

过程监视的主要步骤：

1) 获取测试数据X_new，并使用建模时的均值和标准差对其进行标准化。

2) 在建模时的主元空间提取该样本的主元T_new和计算统计量Q_new，构建新的特征空间X'_new。

3) 在X'中寻找X_new的k(1-q₎和k(1+q)个近邻，并计算距离平方和D_k(1-q)和D_k(1+q)。

4) 当D_k(1-q) < D_lim且D_k_(1+q) > D_lim时新样本更新到训练数据中，并返回执行模型建立的步骤1）。否则执行步骤5）。

5) 当D_k(1-q)≥ D_lim时，表示该生产过程发生异常。

3 仿真结果及分析 3.1 数值仿真

以Ge和Song设计的数值例子^[20]为例。该例子包含5个变量，由以下模型产生

$\begin{array}{l} {x_{\rm{1}}} = {\rm{0}}{\rm{.5768}}{s_1} +0.3766{s_2} +{e_1}\\ {x_{\rm{2}}} = {\rm{0}}.7382{s_1} +0.0566{s_2} +{e_2}\\ {x_{\rm{3}}} = {\rm{0}}.{\rm{8291}}{s_1} +0.4009{s_2} +{e_3}\\ {x_{\rm{4}}} = {\rm{0}}.6519{s_1} +0.2070{s_2} +{e_4}\\ {x_{\rm{5}}} = {\rm{0}}.3972{s_1} +0.8045{s_2} +{e_5} \end{array} $

(6)

其中e₁，e₂, e₃，e₄和e₅是服从[0, 0.01]的白噪声，s₁ ~ U(-10, -7)，s₂ ~ N(-15, 1)。

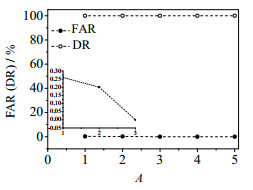
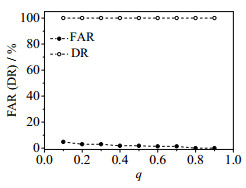
采集1000个样本作为正常数据，为了说明不完整训练数据的情况，分别顺序取正常数据的20%，50%，70%作为训练数据。再采集1000个样本作为检验数据和故障数据，变量x₅在501处加一个幅值为4的阶跃故障，则前500个样本作为检验数据，后500个样本作为故障数据。采用所提方法FS-AkNN分别对样本数为200、500和700的训练数据建立模型进行过程检测。为了对比，文中还给出了PCA、基于特征空间kNN (feature space k nearest neighbor, FS-kNN)方法的检测结果。本文在选取参数时采用交叉验证，交叉验证过程如图 3和4所示。不同参数取值影响检测率(DR)和误报率(FAR)，理想情况下希望在有较大DR的同时FAR较小，所以使用FAR和DR进行交叉验证，确定主元个数为3，k = 5和q = 0.8。图 5是训练数据为正常数据的50%时，PCA、FS-kNN和FS-AkNN的故障检测图。

图 3 不同A时的FAR和DR Fig.3 FAR and DR values at different A

图 4 不同q时的FAR和DR Fig.4 FAR and DR values at different q

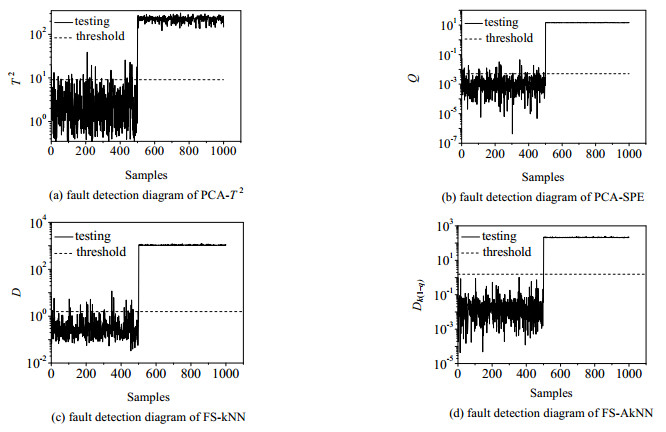
图 5 PCA、FS-kNN和FS-AkNN的故障检测图 Fig.5 Fault detection diagrams of PCA, FS-kNN and FS-AkNN

在确定主元个数及q时，希望在允许误报的范围内得到较小的误报率和较高的检测率。从图 3和4中可知，主元个数为3和q= 0.8时，满足在最小误报率时有最高的检测率。

从图 5(d)可以看出FS-AkNN方法在500时刻检测出故障且误报率为0。图 5(a)，(b)和(c)可以看出PCA和FS-kNN方法虽然能在500时检测出故障，但都存在一定的误报率。

样本数为200、500和700的训练数据建立模型进行故障检测时，PCA、FS-kNN和FS-AkNN的检测率(DR)和误报率(FAR)如表 1所示。

表 1 PCA、FS-kNN和FS-AkNN的检测结果统计表 Table 1 Detection results of PCA, FS-kNN and FS-AkNN

从表 1可以看出，PCA、FS-kNN和FS-AkNN对故障的检测率都达到了100%。但是，PCA和FS-kNN在实现较高检测率的同时，因其对故障的敏感度使其产生较高的误报率，这在实际情况中可能会降低PCA和FS-kNN的可靠性。相比较而言，FS-AkNN在过程监控中表现出可靠的性能，在只有部分训练数据的情况下，它的误报率比PCA和FS-kNN低。而且不同数量的训练数据时误报率的变化范围相对较小，模型更稳定，说明了该方法能够及时更新故障检测模型且具有极高的可靠性。

3.2 TE过程仿真

Tennessee Eastman (TE)过程是由DOWNS和VOGEL提出的基于实际工业过程的仿真实例。此过程由4种反应物(A、C、D、E)和一种惰性气体(B)，生成2种产物(G和H)。整个生产过程以3种不同G/H混合比例构成6种不同的操作模式。选用基本工况，整个过程系统共有12个操纵变量和41个测量变量(含22个连续变量和19个成分变量)。过程模拟包含21个过程故障^[21]。本文选择41个测量变量和11个操纵变量，共52个过程变量。对于TE过程，正常训练数据包含500个采样点，为了说明不完整训练数据的情况，选取正常数据的前100，250和400个样本分别构成训练数据。

采用本文FS-AkNN方法对21个故障进行检测，以故障8和12训练数据采用250个时的检测为例给出分析，为了对比，文中也给出了PCA和FS-kNN的检测结果，检测结果如图 8和10。利用交叉验证确定主元个数为3，k=5和q=0.8，确定过程如图 6和7所示。

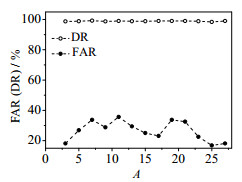
图 6 不同A时的FAR和DR Fig.6 FAR and DR values at different A

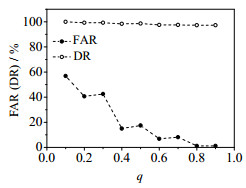
图 7 不同q值时的FAR和DR Fig.7 FAR and DR values at different q

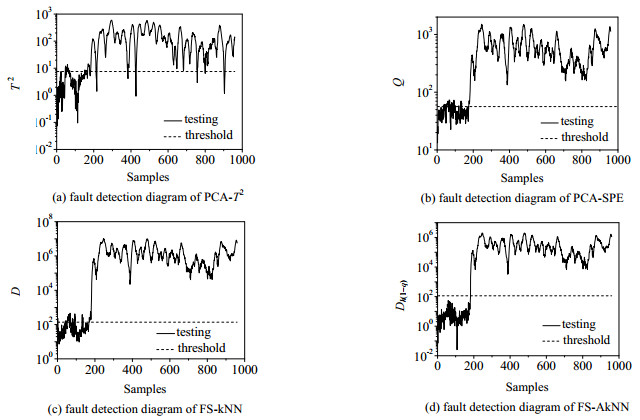
图 8 故障8的PCA、FS-kNN和FS-AkNN的故障检测结果图 Fig.8 Fault 8 detection results of PCA, FS-kNN and FS-AkNN

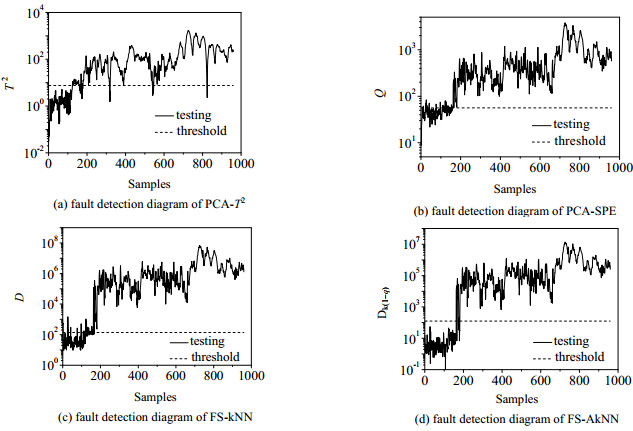
图 10 故障12的PCA、FS-kNN和FS-AkNN的故障检测结果图 Fig.10 Fault 12 detection results of PCA, FS-kNN and FS-AkNN

从图 6和7中可知，主元个数及更新因子不同故障检测率和误报率的变化不同。在满足最小误报率和最大检测率时，主元个数为3，q=0.8。

从图 8(d)中可知使用FS-AkNN方法故障在180时刻被检测出来，误报率为0，从8(a), (b)和(c)中可知使用PCA和FS-kNN方法故障在175时刻被检测出来，虽然比所提方法提早检测出故障，但同时误报率也比其误报率高很多，这可能降低PCA和FS-kNN检测结果的可靠性。

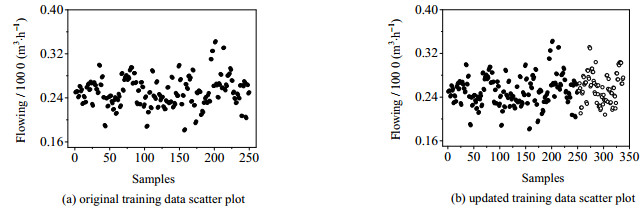
使用FS-AkNN方法对故障8进行检测，变量1 (即物料A的流量)的原始训练数据与仿真结束后(即更新后)的训练数据散点图如图 9所示。

图 9 变量1训练数据散点图 Fig.9 Training data scatter plots of variable 1

在图 9中黑色实心圆代表原始训练数据，空心圆代表更新的数据, 可以看出250个原始训练数据在仿真结束后变为了338个，增加了88个数据，说明在仿真过程中实现了自适应更新。在采用intel(R) Core(TM) i3-4160 CPU@3.60GHz #.60 GHz处理器，4GB内存，Windows10 64位操作系统时，完成一次更新的时间大约为0.022 991 24 s。当工业应用时，可以采用好于本实验的设备，则更新时间更短，所以可以实现实时监测。

从图 10(a)和(b)中可知PCA检测故障12时，故障在161时刻被检测出来，但其误报率很高。10(c)中可知使用FS-kNN方法检测该故障时，故障在162时刻左右被检测出来，同时也伴随着很高的误报率。高误报率可能降低PCA和FS-kNN检测结果的可靠性。但是，从10(d)可知使用FS-AkNN方法检测故障12时，故障在162时刻左右被检测出来且误报率为0，表明了该方法的有效性和可靠性。

21个故障使用PCA、FS-kNN和FS-AkNN检测时的检测率和误报率如表 2和表 3所示。

表 2 不同数量训练数据时PCA、FS-kNN和FS-AkNN的检测率统计表 Table 2 Detection rates of PCA, FS-kNN and FS-AkNN with different amounts of training data

Fault	100				250				400
Fault	PCA-T₂	PCA-SPE	FS-kNN	FS-A-kNN	PCA-T₂	PCA-SPE	FS-A-kNN	FS-AkNN	PCA-T₂	PCA-SPE	FS-kNN	FS-AkNN
fault 1	99.25	100	100	99.75	99.37	100	100	99.62	99.37	100	99.75	99.62
fault 2	98.25	99.75	99.50	98.62	71.37	99.37	99.25	98.37	96.25	99.25	98.75	98.25
fault 3	21.25	85.00	75.12	20.62	24.87	35.00	28.75	2.00	35.75	16.62	29.50	0.37
fault 4	22.88	100	99.88	92.75	17.37	100	100	58.75	33.00	100	98.87	51.12
fault 5	35.00	85.75	77.63	38.62	36.00	55.50	48.87	22.62	42.00	41.25	47.37	23.50
fault 6	99.50	100	100	100	99.62	100	100	100	99.62	100	100	100
fault 7	55.63	100	100	100	53.00	100	100	100	57.50	100	100	100
fault 8	99.75	100	100	98.75	96.37	98.25	98.87	97.50	97.87	98.12	99.25	97.50
fault 9	19.13	82.37	71.00	1.00	24.25	33.50	28.62	0.62	33.75	15.37	29.62	0.25
fault 10	50.70	94.75	91.50	70.87	58.87	74.12	71.75	22.00	63.25	64.50	71.87	15.25
fault 11	39.62	96.63	94.50	61.87	27.87	86.87	84.75	56.12	46.37	81.12	82.25	53.00
fault 12	96.00	100	100	99.87	97.87	100	99.62	99.00	98.12	99.12	99.75	98.87
fault 13	94.50	99.25	98.75	96.25	95.50	96.12	96.12	95.00	95.87	95.62	96.00	94.75
fault 14	75.12	100	100	100	64.25	100	100	99.87	82.37	100	100	100
fault 15	22.88	72.25	61.88	15.12	23.25	32.87	32.00	2.50	28.75	21.25	31.75	0.50
fault 16	43.75	96.75	93.75	8.25	52.25	70.12	68.75	10.87	60.00	56.25	70.25	6.50
fault 17	77.38	97.88	96.50	88.87	70.37	95.62	95.62	84.62	82.87	94.75	95.00	81.62
fault 18	89.00	97.75	96.50	90.50	92.00	93.12	92.50	89.37	92.75	90.87	92.25	89.25
fault 19	13.13	87.88	79.25	11.75	8.62	59.12	47.87	2.25	15.62	44.00	39.50	1.62
fault 20	41.38	96.25	94.13	59.12	54.50	77.75	76.37	40.62	61.62	69.37	76.50	37.50
fault 21	24.88	85.88	80.63	64.87	34.50	68.62	62.87	43.25	39.00	58.87	57.25	40.12

表 2 不同数量训练数据时PCA、FS-kNN和FS-AkNN的检测率统计表 Table 2 Detection rates of PCA, FS-kNN and FS-AkNN with different amounts of training data

表 3 不同数量训练数据时PCA、FS-kNN和FS-AkNN的误报率统计表 Table 3 False alarm rates of PCA, FS-kNN and FS-AkNN with different amounts of training data

Fault	100				250				400
Fault	PCA-T²	PCA-SPE	FS-kNN	FS-AkNN	PCA-T²	PCA-SPE	FS-AkNN	FS-kNN	PCA-T²	PCA-SPE	FS-kNN	FS-AkNN
fault 1	1.25	43.13	26.87	1.25	1.87	20.62	11.87	0	3.75	12.50	10	0
fault 2	2.50	35.63	21.25	1.87	0	16.25	12.50	0.62	0.62	6.87	5.62	0.62
fault 3	13.13	68.13	56.87	0.63	25.62	28.75	25.62	1.87	27.50	13.75	22.50	0
fault 4	2.50	44.37	31.25	7.50	3.12	16.87	8.12	0.62	3.75	10.62	10.62	0
fault 5	2.50	44.37	31.25	7.50	3.12	16.87	8.12	0.62	3.75	10.62	10.62	0
fault 6	2.50	31.25	18.75	3.75	0.62	8.12	4.37	0	2.50	4.37	3.12	0
fault 7	0.63	50.00	33.75	3.75	5.00	6.25	4.37	0	7.50	4.37	2.50	0
fault 8	23.75	69.37	57.50	18.12	14.37	20.00	16.25	0	20.00	7.50	13.12	0
fault 9	13.13	81.87	73.12	6.25	38.12	46.25	42.50	1.25	45.62	15.00	39.37	0.62
fault 10	1.87	56.25	37.50	6.25	2.50	13.12	10.62	0	15.00	6.25	11.87	0
fault 11	4.37	60.62	43.75	6.25	3.75	28.75	18.12	0.62	5.62	15.00	15.62	0
fault 12	14.37	55.63	43.75	11.25	22.50	21.25	22.50	0	21.87	9.37	18.75	0
fault 13	3.75	29.38	15.63	2.5	2.50	10.00	5.62	0	5.00	3.75	2.50	0
fault 14	1.25	50.00	37.50	5.62	6.25	13.75	8.12	0	10.00	8.75	9.37	0
fault 15	2.50	56.87	33.12	7.50	0.62	10.62	5.62	0	1.87	4.37	6.87	0
fault 16	28.13	80.0	73.75	13.75	50.62	46.25	50.62	5	62.50	23.12	50.62	0
fault 17	4.37	54.37	36.88	0.62	3.75	14.37	6.87	0	6.25	8.75	8.75	0
fault 18	10.00	65.63	50.62	8.12	1.25	19.37	13.12	0	5.62	10.62	8.12	0
fault 19	1.25	56.25	41.25	1.87	1.87	16.87	11.25	0	5.62	8.12	11.87	0
fault 20	1.87	39.37	16.88	0.65	1.87	10.62	6.25	0	4.37	3.75	3.12	0
fault 21	11.25	71.25	65.00	13.75	8.75	28.75	24.37	3.75	10.00	14.37	14.37	0
Note: All values in table 2 and 3 are percentage values

表 3 不同数量训练数据时PCA、FS-kNN和FS-AkNN的误报率统计表 Table 3 False alarm rates of PCA, FS-kNN and FS-AkNN with different amounts of training data

表 2为训练样本分别为100，250和400时，PCA、FS-kNN和FS-AkNN 3种方法对21个故障的检测率统计表，表 3为误报率统计表。从表 2和表 3中故障12的检测结果可以看出，当有100个训练数据时PCA的检测率为100%，误报率为55.63%；FS-kNN的检测率为100%，误报率为43.75%；FS-AkNN的检测率为99.87%，误报率为11.25%。虽然PCA和FS-kNN的检测率较高，但对应的误报率也较高，使得该方法的可靠性降低。而FS-AkNN在有较高检测率的同时误报率也较低，使其检测结果更加可靠。当有250个和400个训练数据时也可以得到相同的结论。而且在不同数量训练数据的情况下，FS-AkNN的误报率变化范围比PCA和FS-kNN的误报率变化范围小，模型更稳定。该结论与从数值例子中得到的结论一致，表明该方法的有效性。

4 结论

本文提出了一种特征空间自适应kNN故障检测方法，解决了生产过程中实时数据可能包含建模数据忽略的过程信息，需要及时更新故障检测模型的问题。所提方法与PCA方法和FS-kNN方法相比，在只有部分训练数据的情况下，故障检测模型能够自动更新的同时有较高的检测率和较低的误报率，表明了该方法的有效性和可靠性。在仿真过程中发现，一些故障在检测过程中存在一定的延时报警现象，下一步将针对这个问题进行研究。

符号说明：

参考文献

[1]	QIN S J. Survey on data-driven industrial process monitoring and diagnosis[J]. Annual Reviews in Control, 2012, 36(2): 220-234. DOI:10.1016/j.arcontrol.2012.09.004
[2]	YIN S, LI X, GAO H, et al. Data-based techniques focused on modern industry:An overview[J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 657-667. DOI:10.1109/TIE.2014.2308133
[3]	马贺贺.基于数据驱动的复杂工业过程故障检测方法研究[D].上海: 华东理工大学, 2013. MA H H.Research on fault detection method for complex industrial process based on data driven[D].Shanghai: East China University of Science and Technology, 2013.
[4]	MISRA M, YUE H H, QIN S J, et al. Multivariate process monitoring and fault diagnosis by multi-scale PCA[J]. Computers & Chemical Engineering, 2002, 26(9): 1281-1293.
[5]	WANG Q, LIU Y B, HE X, et al. Fault diagnosis of bearing based on kPCA and kNN method[J]. Advanced Materials Research, 2014, 986.
[6]	张汉元, 田学民. 基于异步PCA的故障识别方法)[J]. 高校化学工程学报, 2016, 30(3): 680-685. ZHANG H Y, TIAN X M. Fault identification method based on asynchronous PCA[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(3): 680-685. DOI:10.3969/j.issn.1003-9015.2016.03.026
[7]	刘康玲.基于自适应PCA和时序逻辑的动态系统故障诊断研究[D].杭州: 浙江大学, 2017. LIU K L.Research on fault diagnosis of dynamic system based on adaptive PCA and sequential logic[D].Hangzhou: Zhejiang University, 2017.
[8]	HE Q P, WANG J W J. Fault detection using the k-nearest neighbor rule for semiconductor manufacturing processes[J]. IEEE Transactions on Semiconductor Manufacturing, 2007, 20(4): 345-354. DOI:10.1109/TSM.2007.907607
[9]	LI W, YUE H H, VALLE-CERVANTES S, et al. Recursive PCA for adaptive process monitoring[J]. Journal of Process Control, 2000, 10(5): 471-486. DOI:10.1016/S0959-1524(00)00022-6
[10]	WOLD S. Exponentially weighted moving principal components analysis and projections to latent structure[J]. Chemometrics & Intelligent Laboratory Systems, 1994, 23(1): 149-161.
[11]	LEE D S, VANROLLEGHEM P A. Monitoring of a sequencing batch reactor using adaptive multiblock principal component analysis[J]. Biotechnology and Bioengineering, 2003, 82(4): 489-497. DOI:10.1002/(ISSN)1097-0290
[12]	LEE D S, PARK J M, VANROLLEGHEM P A. Adaptive multiscale principal component analysis for on-line monitoring of a sequencing batch reactor[J]. Journal of Biotechnology, 2005, 116(2): 195-210.
[13]	LENNOX J, ROSEN C. Adaptive multiscale principal components analysis for online monitoring of wastewater treatment[J]. Water Science & Technology A Journal of the International Association on Water Pollution Research, 2002, 45(4-5): 227.
[14]	杨丰铭. 基于自适应PCA的油田生产故障诊断方法[J]. 化工管理, 2017(18): 21-21. YANG F M. Oilfield production fault diagnosis method based on adaptive PCA[J]. Chemical Industry Management, 2017(18): 21-21. DOI:10.3969/j.issn.1008-4800.2017.18.019
[15]	张媛媛, 韩少廷, 耿志强, 等. 自适应移动窗递推PCA过程监测方法研究)[J]. 计算机与应用化学, 2011, 28(8): 1022-1026. ZHANG Y Y, HAN S T, GENG Z Q, et al. Research on monitoring method of recursive PCA process with adaptive mobile window[J]. Computers and Applied Chemistry, 2011, 28(8): 1022-1026. DOI:10.3969/j.issn.1001-4160.2011.08.016
[16]	RYU S R, NODA I, JUNG Y M. Moving window principal component analysis for detecting positional fluctuation of spectral changes[J]. Bulletin-Korean Chemical Society, 2011, 32(7): 2332-2338. DOI:10.5012/bkcs.2011.32.7.2332
[17]	郭小萍, 袁杰, 李元. 基于特征空间k最近邻的批次过程监视[J]. 自动化学报, 2014, 40(1): 135-142. GUO X P, YUAN J, LI Y. Batch process monitoring based on k-nearest neighbor in feature space[J]. Acta Automatica Sinica, 2014, 40(1): 135-142.
[18]	郭金玉, 王鑫, 李元. 基于加权差分主元分析的化工过程故障检测[J]. 高校化学工程学报, 2018, 32(1): 186-196. GUO J Y, WANG X, LI Y. Chemical process fault detection based on weighted difference principal component analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(1): 186-196.
[19]	ZHU W, SUN W, ROMAGNOLI J A. Adaptive k-nearest-neighbor method for process monitoring[J]. Industrial & Engineering Chemistry Research, 2018, 57(7): 2574-2586.
[20]	GE Z, SONG Z. Multimode process monitoring based on Bayesian method[J]. Journal of Chemometrics, 2010, 23(12): 636-650.
[21]	周东华, 李钢, 李元. 数据驱动的工业过程故障诊断技术[M]. 北京: 科学出版社, 2011. ZHOU D H, LI G, LI Y. Data driven industrial process fault diagnosis technology[M]. Beijing: Science Press, 2011.