2. 中国科学院空间应用工程与技术中心 中国科学院太空应用重点实验室,北京 100094
2. Key Laboratory of Space Utilization, Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences, Beijing 100094, China
管式除雾器是一种利用螺旋上升气流产生的离心力分离烟气中惯性较大液滴的重要设备。相比波形板除雾器,管式除雾器的分级除雾效率和总除雾效率较高[1-3],并且具有安装工期短、省电节水、占用空间小、运行维护费用低等特点[4-9]。然而,管式除雾器在运行中产生较高的流动阻力,影响系统安全运行以及增加风机运行能耗。董聪等[10]通过改变翅片倾斜角降低螺旋通道的流动阻力损失。李雅侠等[11]采用高低双螺旋翅片降低螺旋翅片管的流动阻力。姜衍更等[12]提出在翅片表面开孔降低管式除雾器运行阻力。杨来顺等[3]分析了翅片开孔数量对减小流动阻力的作用。结果表明,通过在翅片开孔可以有效减小管式除雾器流动阻力。然而,关于开孔管式除雾器结构优化设计的研究尚未见到。
传统的除雾器设计方法需要进行大量物理或者数学模型实验。然而,由于带孔管式除雾器的结构复杂性,很难快速优化产品结构。近年来,遗传算法(genetic algorithm,GA)指导了多种分离器的多目标优化设计[13-16]。本文通过计算流体力学(computational fluid dynamics,CFD)软件Fluent研究带孔管式除雾器结构因素对除雾性能和流动特性的影响,并通过响应面法(response surface method,RSM)拟合关联式,然后利用GA对除雾器进行多目标优化设计,得到一系列高效低阻开孔管式除雾器的结构尺寸。
2 结构尺寸及数学模型 2.1 结构尺寸采用的带孔管式除雾器物理模型及详细结构尺寸参数如图 1所示。可以看到,管式除雾器包含若干尺寸参数,其中,重要结构参数包括:螺距P、翅片直径D2与尾管长L2。其他结构尺寸采取以下数值:内管直径D3 = 120 mm,外管直径D1 = D2 + 50 mm,间隔A、B = 20 mm,孔宽= 20 mm,翅片厚度= 9 mm,外管长度L1 = P+ 400 mm。设计变量及其取值详见表 1。响应变量为除雾效率与压降,其中,除雾效率定义为捕捉液滴的质量流量与入口液滴质量流量之比,压降为除雾器进出口压差。

|
图 1 开孔管式除雾器结构示意图 Fig.1 Schematic diagram of tube demister with punched holes |
|
|
表 1 设计变量及取值 Table 1 Design variables and values |
利用欧拉-拉格朗日方法分别求解气液两相流运动。气体的运动假设为三维、不压缩的稳态、无换热流动。除了气体运动的连续方程与动量方程,需要另外求解雷诺应力方程、湍动能方程和湍流耗散率方程。该方程描述详见文献[13]~[16]。
在连续相运动求解结束后,采用拉格朗日方法求解液滴(离散相)的运动轨迹。液滴受力方程如式(1)~ (4)所示。
| $ {\text{d}{{\upsilon }_{i\text{p}}}}/{\text{d}t}\;={{F}_{\text{D}}}\left( {{\upsilon }_{i}}-{{\upsilon }_{i\text{p}}} \right)+{g\left( {{\rho }_{\text{p}}}-\rho \right)}/{{{\rho }_{\text{p}}}}\; $ | (1) |
| $ {{F}_{\text{D}}}={18\mu {{C}_{\text{D}}}R{{e}_{\text{p}}}}/{24{{\rho }_{\text{p}}}d_{\text{p}}^{2}}\; $ | (2) |
| $ {{C}_{\text{D}}}=\left\{ \begin{align} & {24}/{R{{e}_{\text{p}}}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ R{{e}_{\text{p}}}\le 1\ \ }\; \\ & {\left( 1\text{+0}\text{.15}Re_{\text{p}}^{0.687} \right)24}/{R{{e}_{\text{p}}}}\;, \ \ \ \ 1<R{{e}_{\text{p}}}\le 1\ 000 \\ & 0.44, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 1\ 000<R{{e}_{\text{p}}} \\ \end{align} \right. $ | (3) |
| $ R{{e}_{\text{p}}}={\rho {{d}_{\text{p}}}\left| {{\upsilon }_{i\text{p}}}-{{\upsilon }_{i}} \right|}/{\mu }\; $ | (4) |
式中:υi,ρ和g分别代表气体速度、气体密度和重力加速度。下标p表示液滴。FD(υi-υip)表示曳力。
在求解过程中,连续相采用空气物性,液滴假设为不变形圆球,运动过程中不存在形变,忽略液滴间碰撞、破碎与蒸发,液滴撞击管壁立即被捕捉,即无空气对液膜的二次夹带作用。使用SIMPLE算法耦合速度场与压力场。离散格式均采用二阶迎风格式,计算收敛以残差值≤ 10-5为准。计算中设置空气密度为1.093 kg·m-3,运动黏度17.95×10-6 m2·s-1,液滴密度采用脱硫浆液密度1 200 kg·m-3,液滴直径分布服从Rosin-Rammler分布,最大与最小直径分别为80与2 μm。除雾器入口处的液滴流速与空气流速相同,液滴质量流量为0.004 75 kg·s-1。
3 计算方法验证由于开孔螺旋翅片的复杂性,翅片区域网格采用适应性较好的非结构化网格,其他区域采用结构化网格。在网格独立性验证时,采用不同密度的4种网格划分方式,模型的总网格数量分别达到36×104,58×104,90×104和142×104。图 2对比了不同网格数下除雾效率与压降变化情况。当网格数从90×104增加至142×104时,压降与除雾效率分别降低了2.6%与0.27%,考虑到模拟结果的准确性与高效性,采取第3种划分方式作为此次研究的网格划分方式。

|
图 2 网格独立性验证 Fig.2 Grid independence verification |
目前,关于开孔螺旋除雾器的实验较少。为了验证所采用计算方法的准确性,根据已发表的螺旋分离器实验[17-18]建立相同尺寸螺旋分离器模型。模拟结果与实验结果对比情况详见图 3。在图中,模拟结果与实验结果的压降误差均方根为5.2%,除雾效率误差均方根为3.7%。说明预测结果与实验结果比较吻合,采用的连续相、离散相模型及计算方法较可行。
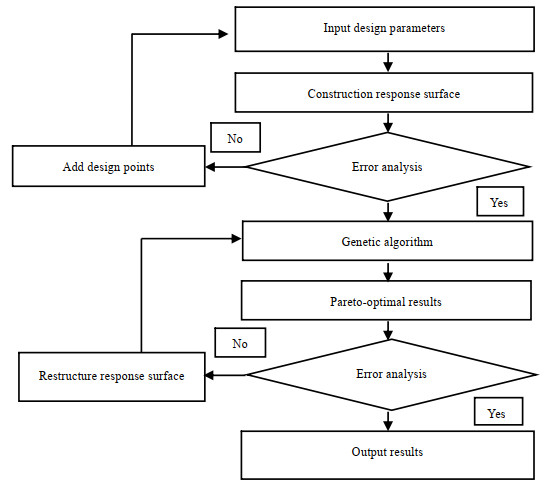
4 优化设计方法借助CFD、RSM和GA综合设计方法对开孔管式除雾器进行多目标优化设计。分析设计变量(翅片直径、螺距、管长和入口流速)对除雾效率和压降的单因素和多因素影响,通过RSM建立数学关系式,并利用NSGA-Ⅱ进行多目标优化设计,得到了一系列帕累托最优点集,这些点包含了具有较高除雾效率和较低流动阻力的除雾器结构。多目标优化设计流程见图 4。
|
图 4 多目标优化设计流程图 Fig.4 Flow chart of the multi-objective optimal design |
RSM是一种统计学方法,用来建立输入变量(设计变量)与输出变量(响应变量)的数学关系。中心合成设计(CCD)是一种实验设计方法,可以用较少的实验点实现较高精度的预测[19-23]。本研究使用Design Expert软件执行CCD与RSM。表 2列出了由CCD得到的部分实验点。通过CFD得到CCD实验点的计算结果后,使用RSM拟合设计变量与响应变量之间的二次多项式,见式(5)。
|
|
表 2 中心合成设计提供的管式除雾器设计点 Table 2 Design cases of tube demister for central composite design |
| $ y={{a}_{0}}+\sum\limits_{i=1}^{n}{{{a}_{i}}{{z}_{i}}}+\sum\limits_{i=1}^{n-1}{\sum\limits_{j=i+1}^{n}{{{a}_{ij}}{{z}_{i}}}}{{z}_{j}}+\sum\limits_{i=1}^{n}{{{a}_{ii}}z_{i}^{2}} $ | (5) |
式中:n为设计变量数量,a0,ai,aij和aii为多项式参数。y为输出变量(响应变量),此处代表除雾效率和压降,z为输入变量(设计变量)。
4.2 多目标优化GA是一种模拟自然生物进化的随机全局搜索方法。遗传算法从一定数量的随机初始值(亲本种群)开始,然后根据具体问题从亲本种群中选择一些个体。通过选择、交叉和变异等一系列操作,从选定的亲本种群个体中产生后代种群。在父母和后代群体中表现较好的个体将被选为下一个父母群体,而其他个体则被抛弃。一般来说,在每一代中,有益的特性都会被保存下来,同时也产生新的特性。这一过程导致了更适合环境的个体群体的进化[24-27]。
在实际工程问题中,经常存在多个目标函数,它们之间相互冲突,不能同时进行取得最优值。近年来,基于帕累托最优性的多目标优化算法层出不穷,并取得了比较理想的优化效果。例如,非支配排序遗传算法(NSGA)[24]、多目标遗传算法(MOGA)[25]和非支配排序遗传算法-Ⅱ(NSGA-Ⅱ)[26]。NSGA-Ⅱ算法可以快速、准确进行多目标优化[19-23],这种算法引入了快速非支配排序算法和精英保留策略,即将父代种群与子代种群合并,将非支配排序层级作为个体适应度值,最后保留最优个体,并通过拥挤距离的计算机制保持种群的多样性。该算法可以规避人因错误因素,排除传统归一化权重因子造成的主观经验影响[26]。因此,本研究采用NSGA-Ⅱ对开孔管式除雾器进行多目标优化设计。
4.3 RSM拟合将CCD提供的25个实验点以及单因素分析的设计点建模并进行CFD计算,通过RSM拟合设计变量(螺距P、直径D2、管长L2和入口流速υ)与响应变量(除雾效率和压降)之间的二次多项式。关联式见式(6)和(7),系数如表 3所示。
|
|
表 3 关联式系数 Table 3 Coefficients of correlations |
| $ \begin{array}{l} {\rm{Separation efficiency / \% = }}{b_{\rm{0}}} + {b_1}L2 + {b_2}P + {b_3}D2 + {b_4}\upsilon \\ + {b_5}L2P + {b_6}PD2 + \\ {b_7}P\upsilon + {b_8}{(L2)^2} + {b_9}{P^2} + {b_{10}}{(D2)^2} + {b_{11}}{\upsilon ^2} \end{array} $ | (6) |
| $ \begin{array}{l} {\rm{Pressure drop / Pa = }}{c_{\rm{0}}} + {c_1}P + {c_2}D2 + {c_3}\upsilon + {c_4}PD2 + \\ {c_5}P\upsilon + {c_6}D2\upsilon + \\ {c_7}{P^2} + {c_8}{(D2)^2} + {c_9}{\upsilon ^2} \end{array} $ | (7) |
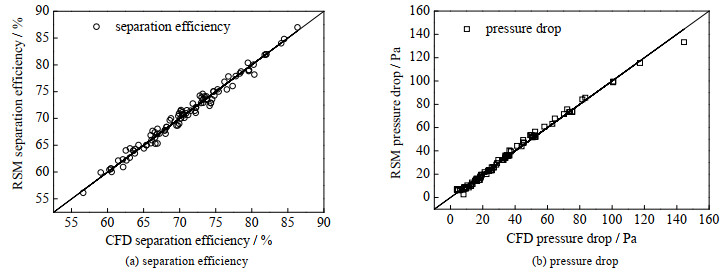
在得到关联式后,为验证其精度,与CFD模拟结果进行对比。对比结果如图 5所示。另外,RSM拟合关联式精度还可以通过计算R2进行二次校对,其定义如式(8)所示。
|
图 5 RSM预测精度 Fig.5 Fitting precision of RSM |
| $ {{\rm{R}}^2} = 1 - \frac{{\sum\nolimits_{i = 1}^n {{{\left( {{y_i} - {y_i}^*} \right)}^2}} }}{{\sum\nolimits_{i = 1}^n {{{\left( {{y_i} - \overline y } \right)}^2}} }} $ | (8) |
式中:yi是第i个CFD算例的响应值,yi*为第i个RSM点的响应值,y是所有yi的算数平均值。R2值越接近100%,RSM拟合关联式精度越高。在此算例中,除雾效率与压降的R2值分别为98.5%和99.3%,说明二次多项式与CFD结果较为一致。为了进一步验证RSM拟合关联式的预测精度,分别计算了关联式与数值预测除雾效率和压降的均方根误差
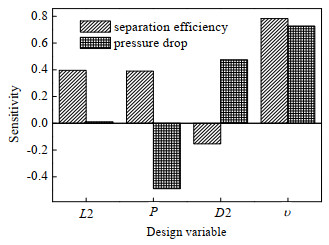
本节讨论单个设计变量变化对除雾性能的影响。图 6为除雾效率与压降对4个设计变量的敏感度,该敏感度的计算基于协方差。由图可见,管长、螺距和入口流速对除雾效率有正作用;螺距对压降有负相关;直径与入口流速对压降有正相关;管长对压降的影响极其微小。
|
图 6 设计变量敏感度 Fig.6 Sensitivity of investigated variables |
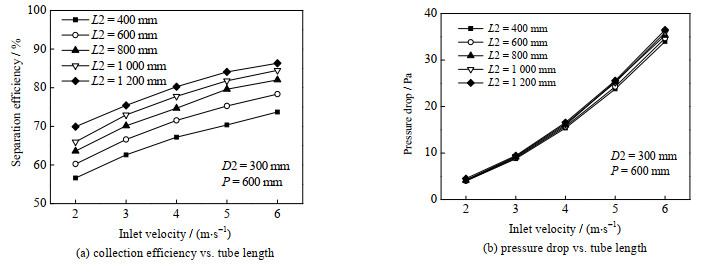
在不同流速下,管长L2对开孔管式除雾器的除雾效率及压降的影响见图 7。其中,翅片直径为300 mm,螺距为600 mm。由图可见,随着入口速度的增加,除雾效率增加,增速逐渐减缓;而压降也随着入口速度的增加而增大,曲线逐渐陡峭。但管长对压降的影响不明显。当管长从400 mm增加到1 200 mm时,除雾效率增加了17.1%~23.5%,压降增加了7.3%~13.4%。主要原因是随着管长的增加,导致捕获液滴的面积增加,从而提高了分离效率。而直管长度造成沿程阻力损失很小,因此管长越长,带孔管式除雾器除雾效率越高。
|
图 7 管长对性能的影响 Fig.7 Effects of pipe length on performance |
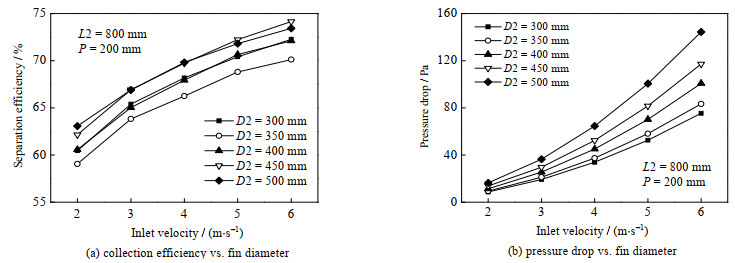
图 8(a)展示了直径D2对除雾效率的影响。其中,管长与螺距分别为800与200 mm。可以看出,D2 = 450 mm时的除雾效率接近于D2 = 500 mm,且D2 = 300 mm和400 mm的除雾效率呈现相似的关系,D2 = 350 mm时除雾效率最小。分析其原因,增加直径,使管式除雾器流场内切向速度增加,有利于液滴被壁面捕捉分离。然而,翅片开孔面积随着直径的增加而增大,反而增加了流场内轴向速度,且使得更多液滴从开孔穿过,直接离开除雾器,不利于除雾效率的增加。两方面共同作用导致除雾效率产生波动。从图 8(b)可以看出,随着翅片直径的增大,压降急剧增大,且流速越高,压降损失越大。分析其原因,在保持螺距不变情况下,翅片直径的增加使得叶片更加扁平,因此产生更强烈的旋转,并且流动路径更长,增加了流动阻力。
|
图 8 翅片直径对性能的影响 Fig.8 Effects of fin diameter on performance |
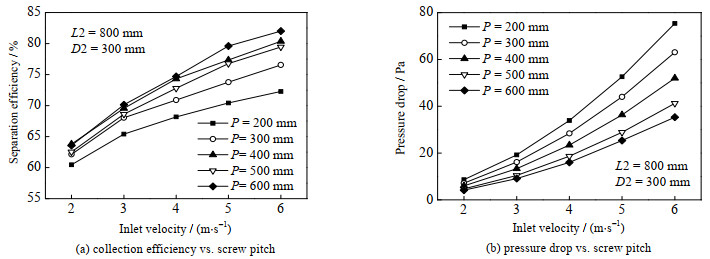
图 9为当管长为800 mm、翅片直径为300 mm时,除雾效率和压降随着螺距P的变化趋势。如图所示,除雾效率随着螺距的增加而增大,压降随着螺距的增加而减小。随着螺距从200升高到600 mm,除雾效率提高了5.2%~13.5%,压降降低了51.7%~53.2%。这是因为,翅片螺距增加导致螺旋通道加长,液滴加速时间增加,并且吸附液滴的管壁面积增加,有利于液滴分离。当翅片直径不变时,螺距的增加导致螺旋路径更平缓,减小了翅片的形状阻力。
|
图 9 螺距对性能的影响 Fig.9 Effects of screw pitch on performance |
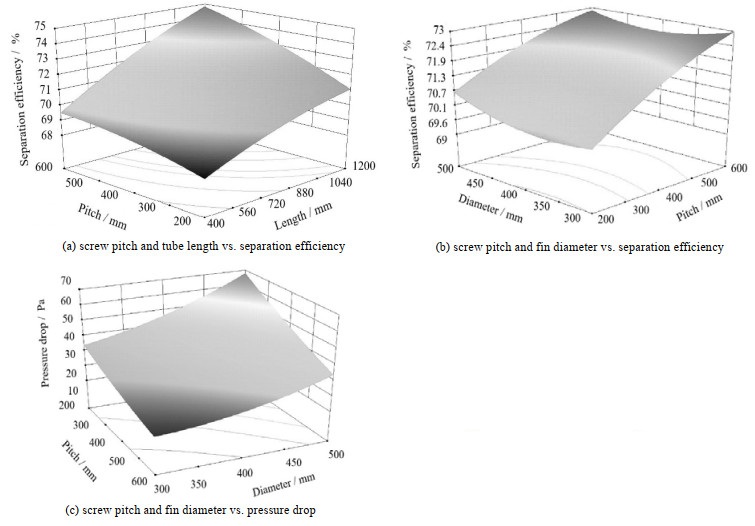
本研究中包含4个设计变量与2个响应变量,通过3维曲面讨论设计变量对响应变量的综合影响。图 10(a)中,翅片直径和进口速度分别为400 mm和4 m·s-1。图 10(b)、(c)中,L2 = 800 mm,υ = 4 m·s-1。图 10(a)说明,当翅片直径和进口速度分别为400 mm和4 m·s-1时,增加螺距或管长均可以提高除雾效率,与单因素分析的结论相符。在图 10(b)中,直径和螺距对除雾效率的综合影响出现“U形”的趋势,较大的螺距更有利于除雾效率的提升,并且当直径取500或300 mm,螺距取600 mm时除雾效率较高。从图 10(c)可以看出,在所研究的范围内,当螺距较大时,减小直径的减阻效果更加明显。
|
图 10 多因素综合影响 Fig.10 Combined effects of multiple factors |
如上所述,4个设计变量对2个目标函数的影响程度不同。而且,除雾效率与压降之间受某些变量的影响存在着相反的趋势。因此,此最优值问题没有唯一解,需要多目标优化来解决。带孔管式除雾器的多目标优化问题可以用式(9)表示。
| $ \left\{ \begin{array}{l} {\rm{Maximize}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Separation efficiency / \% = }}{y_1}\left( {L2, D2, P, \upsilon } \right)\\ {\rm{Minimize}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Pressure}}\;{\rm{drop / Pa = }}{y_2}\left( {L2, D2, P, \upsilon } \right)\\ {\rm{Subject}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{to }}\;400\;{\kern 1pt} {\rm{mm }} \le L2 \le 1\;200\;{\kern 1pt} {\rm{mm}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 300\;{\kern 1pt} {\rm{mm}} \le D2 \le 500\;{\kern 1pt} {\rm{mm}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 200{\kern 1pt} \;{\rm{mm}} \le P \le 600\;{\kern 1pt} {\rm{mm}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2\;{\kern 1pt} {\rm{m}} \cdot {{\rm{s}}^{ - {\rm{1}}}} \le \upsilon \le 6{\kern 1pt} \;{\rm{m}} \cdot {{\rm{s}}^{ - {\rm{1}}}} \end{array} \right. $ | (9) |
在拟合出目标变量与调查变量之间的多项式后(式(6)、(7)),利用MATLAB软件编程,使用NSGA-Ⅱ算法得到帕累托优化结果。在本研究中,初始样本数和每次迭代的样本数均选择为100,每个自变量的二进制序列长度为20,迭代次数最多不超过100步。交叉可能性和变异可能性分别为0.9和0.7 / Lind (Lind为每个个体的二进制序列长度)。
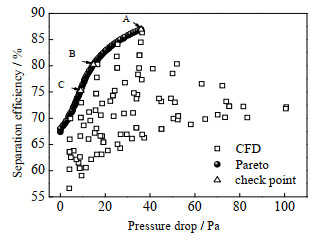
图 11显示了关于开孔管式除雾器的一系列帕累托最优点,其中的每个点包含了关于两个目标函数和四个设计变量的综合信息。结果表明,与以往的CFD预测结果(4.3和5.1节)相比,在相同的压降情况下,帕累托优选点实现了更大的除雾效率。而在相同的除雾效率下,帕累托最优点展现了较小的压降。其中,帕累托最优点的压降最大值约为36 Pa,同时除雾效率达到86%。优化点的管长与螺距接近所限定范围的最大值,符合上文得到的单因素影响规律。为了验证多目标设计结果预测准确性,从帕累托优化点集手动选择3个点(图 11,A、B、C点),根据3个点的结构建立模型并通过计算流体力学软件进行计算,预测结果与帕累托点集进行对比,从而验证点集的准确性(表 4)。注意到,对比结果之间显示出较好一致性,说明帕累托最优点预测结果较准确。表 5将帕累托优化点与文献[3]的初始设计方案进行了对比,在与初始设计对比[3]时,流速采用与初始设计相同工况,直径的取值以“除雾效率较高”为准,管长和螺距基本为固定值,分别为1 200和600 mm,这与单因素、多因素分析的结果吻合。可以看出,在相同的入口流速下,帕累托优化点的除雾效率提升了12.9%~20.2%,流动阻力降低了52.9%~60.5%。因此,开孔管式除雾器的帕累托最优点普遍具有较小的压降和较高的除雾效率,该点集可以为除雾器的工业应用设计提供指导。
|
图 11 帕累托优化结果与CFD结果对比 Fig.11 Comparison of Pareto-optimal points and CFD simulations |
|
|
表 4 帕累托优化点的数值验证结果 Table 4 Validated results of Pareto-optimal points |
|
|
表 5 帕累托优化点与初始设计对比 Table 5 Comparison of Pareto-optimal points and initial design |
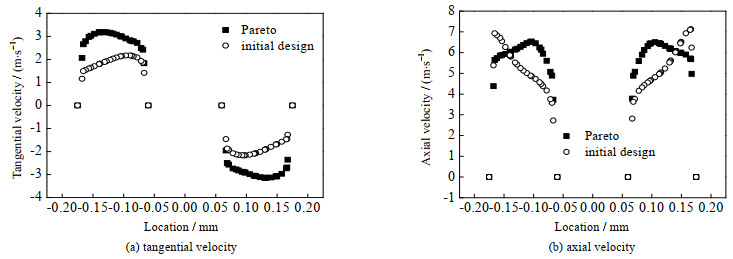
图 12展示了螺旋翅片尾部下游200 mm处的切向速度和轴向速度分布,其中的帕累托与初始设计结构参考表 5。切向速度作为影响管式除雾器液滴分离效率的主要因素,在优化后得到了强化,切向速度整体增大,最大值提高了44.7%且分布均匀,有利于液滴分离。轴向速度的分布相比初始设计更加均匀,靠近内管的螺旋翅片尾部低速区减小,涡流损耗降低,有利于减小管式除雾器的流动阻力。
|
图 12 切向速度与轴向速度 Fig.12 Tangential and axial velocity distributions |
通过计算流体力学软件Fluent对带孔管式除雾器性能的影响因素进行了研究,讨论了结构因素对性能和流动的单因素和多因素影响,借助响应面法拟合了目标函数与设计变量之间的关系式,并采用NSGA-Ⅱ算法完成了多目标优化设计。得到结论如下:
(1) 利用响应面法可以通过较少的试验点拟合关于目标函数和设计变量的二次多项式,且具有较高的精度。
(2) 开孔除雾器的管长、螺距和入口流速对除雾效率有正作用;螺距对压降有负相关;直径与入口流速对压降有正相关;管长对压降的影响极其微小。在所研究的范围内,螺距为600 mm、管长取1 200 mm时除雾效率较高;直径为300 mm或螺距为600 mm时阻力最小。
(3) 通过多目标优化得到了一系列高效低阻的管式除雾器设计点。与初始设计相比,利用NSGA-Ⅱ算法得到的帕累托优化点除雾效率提升了12.9%~20.2%,流动阻力降低了52.9%~60.5%。
| [1] |
朱凯, 袁竹林. 一种涡流除雾器的实验与数值模拟研究[J]. 中南大学学报(自然科学版), 2018, 49(1): 22-30. ZHU K, YUAN Z L. Experimental study and numerical simulation of one kind of vortex demister[J]. Journal of Central South University (Science and Technology), 2018, 49(1): 22-30. |
| [2] |
杨来顺, 徐明海, 孙宪航, 等. 涡发生器对脱硫系统除雾器性能的影响[J]. 化工进展, 2019, 38(6): 2600-2609. YANG L S, XU M H, SUN X H, et al. Influence of different vortex generators on performance of demister in wet flue gas desulfurization[J]. Chemical Industry and Engineering Progress, 2019, 38(6): 2600-2609. |
| [3] |
杨来顺, 徐明海, 陈秋实. 管式除雾器开孔对除雾性能影响的数值模拟研究[J]. 中国电力, 2018, 51(7): 178-184. YANG L S, XU M H, CHEN Q S. Numerical simulation on separation performance of tube mist eliminator with holes[J]. Electric Power, 2018, 51(7): 178-184. |
| [4] |
高武军, 单永华, 苑斌, 等. 单塔一体化脱硫除尘技术在定州电厂的应用研究[J]. 中国高新技术企业, 2016(16): 85-87. GAO W J, SHAN Y H, YUAN B, et al. Application of single tower desulfurization and dust removal technology in Dingzhou power plant[J]. China High-Tech Enterprises, 2016(16): 85-87. DOI:10.13535/j.cnki.11-4406/n.2016.16.041 |
| [5] |
周文森. 管束除尘除雾技术在燃煤发电机组深度除尘改造中的运用[J]. 工艺与技术, 2016(12): 109-110. ZHOU W S. Application of tube bundle dedusting and fogging technology in deep dedusting renovation of coal-fired generating units[J]. Gongyi Yu Jishu, 2016(12): 109-110. |
| [6] |
周冠旭. 管束式除尘除雾技术在火电机组超低排放改造中的应用[J]. 科技展望, 2016, 26(31): 109-109, 111. ZHOU G X. Application of tube bundle dedusting and fogging technology in the transformation of ultra-low emission of thermal power unit[J]. Science and Technology, 2016, 26(31): 109-109, 111. |
| [7] |
代兵. 管束式除尘除雾器在海水脱硫电厂中的应用[J]. 电力与能源, 2017, 38(5): 606-608. DAI B. Application of dust and mist removal devices of tube bundle type in seawater desulfurization power plant[J]. Power & Energy, 2017, 38(5): 606-608. |
| [8] |
刘海龙, 蔡向东. 管束式除尘装置与湿式静电除尘装置在电厂的应用分析[J]. 华北电力技术, 2017(9): 65-70. LIU H L, CAI X D. Application analysis of tubular precipitator and wet electrostatic precipitator in power plant[J]. North China Electric Power, 2017(9): 65-70. |
| [9] |
邓辉鹏. 火电厂烟气超低排放技术研究[J]. 华电技术, 2016, 38(2): 65-67, 80. DENG H P. Researches on the technology of the flue-gas ultra clean emission of the coal-fired plant[J]. Huadian Technology, 2016, 38(2): 65-67, 80. |
| [10] |
董聪, 陈亚平, 吴嘉峰. 倾斜角对周向重叠三分螺旋折流板换热器性能的影响[J]. 中南大学学报(自然科学版), 2018, 47(6): 2133-2140. DONG C, CHEN Y P, WU J F. Impacts of incline angle on performances of circumferential overlap trisection helical baffle heat exchangers[J]. Journal of Central South University (Science and Technology), 2018, 47(6): 2133-2140. |
| [11] |
李雅侠, 张腾, 张春梅, 等. 高低双螺旋片强化套管换热器壳侧换热[J]. 化工进展, 2016, 35(4): 1042-1046. LI Y X, ZHANG T, ZHANG C M, et al. Heat transfer enhancement on shells of double-pipe exchanger with double helix fins[J]. Chemical Industry and Engineering Progress, 2016, 35(4): 1042-1046. |
| [12] |
姜衍更, 李蜀生.高效多管螺旋除雾除尘装置: 中国, 204469408[P]. 2015-07-15. JIANG Y G, LI S S. High efficiency multi-pipe spiral mist and dust removal device: CN, 204469408[P]. 2015-07-15. |
| [13] |
DIXIT P, TIWARI R, MUKHERJEE A K, et al. Application of response surface methodology for modeling and optimization of spiral separator for processing of iron ore slime[J]. Powder Technology, 2015, 275: 105-112. |
| [14] |
SAFIKHANI H. Modeling and multi-objective Pareto optimization of new cyclone separators using CFD, ANNs and NSGA Ⅱ algorithm[J]. Advanced Powder Technology, 2016, 7: 2277-2284. DOI:10.1016/j.apt.2016.08.017 |
| [15] |
SUN X, KIM S, YANG S D, et al. Multi-objective optimization of a Stairmand cyclone separator using response surface methodology and computational fluid dynamics[J]. Powder Technology, 2017, 320: 51-65. |
| [16] |
SUN X, YOON J Y. Multi-objective optimization of a gas cyclone separator using genetic algorithm and computational fluid dynamics[J]. Powder Technology, 2018, 325: 347-360. |
| [17] |
HOEKSTRA A J. Gas flow field and collection efficiency of cyclone separators[D]. Delft: Delft University of Technology, 2000.
|
| [18] |
EHTERAM M A, TABRIZI H B, MESBAH M, et al. Experimental study on the effect of connecting ducts on demisting cyclone efficiency[J]. Experimental Thermal and Fluid Science, 2012, 39: 26-36. |
| [19] |
WEN J, LI K, ZHANG X, et al. Optimization investigation on configuration parameters of serrated fin in plate-fin heat exchanger based on fluid structure interaction analysis[J]. International Journal of Heat and Mass Transfer, 2018, 119: 282-294. DOI:10.1016/j.ijheatmasstransfer.2018.11.023 |
| [20] |
WANG S, XIAO J, WANG J, et al. Application of response surface method and multi-objective genetic algorithm to configuration optimization of Shell-and-tube heat exchanger with fold helical baffles[J]. Applied Thermal Engineering, 2018, 129: 512-520. |
| [21] |
WANG S, JIAN G, XIAO J, et al. Optimization investigation on configuration parameters of spiral-wound heat exchanger using genetic aggregation response surface and multi-objective genetic algorithm[J]. Applied Thermal Engineering, 2017, 119: 603-609. |
| [22] |
WEN J, YANG H, TONG X, et al. Optimization investigation on configuration parameters of serrated fin in plate-fin heat exchanger using genetic algorithm[J]. International Journal of Thermal Sciences, 2016, 101: 116-125. |
| [23] |
WEN J, YANG H, TONG X, et al. Configuration parameters design and optimization for plate-fin heat exchangers with serrated fin by multi-objective genetic algorithm[J]. Energy Conversion and Management, 2016, 117: 482-489. |
| [24] |
SRINIVAS N, DEB K. Muiltiobjective optimization using nondominated sorting in genetic algorithms[J]. Evolutionary Computation, 1994, 2: 221-248. |
| [25] |
FONSECA C M, FLEMING P J. Genetic algorithms for multiobjective optimization: Formulation discussion and generalization[C]//Genetic Algorithms: Proceedings of the Fifth International Conference (S. Forrest, ed.). San Mateo: Morgan Kaufmann, 1993, 416-423.
|
| [26] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. |
| [27] |
CHIPPERFIELD A, FLEMING P, POHLHEIM H, et al. Genetic algorithm toolbox for use with Matlab[M]. Sheffield: University of Sheffield, 1994.
|





