随着微加工技术的发展,采用具有高面体比的微通道热沉成为冷却高功率密集型微电子设备的有效方法之一,被广泛应用于微电子技术、能源、军工核能、生物化工等先进工程领域[1-4]。根据微通道对流换热理论,可以通过增大通道传热表面积或提高流体的传热性能来提高微通道热沉的传热性能,如可在壁面侧面设置粗糙元[5-6]、采用单相或沸腾传热的方式及使用导热系数更高的纳米流体等工质[7-9]。
已有研究[10-12]表明,复杂结构微通道热沉的传热性能优异,因为通道截面的连续变化能够打断热边界层发展,使流动与传热一直处于未充分发展状态,起到强化传热的目的;此外,通道内部设置粗糙元,能增强内部扰动,进而对流动与传热特性产生重要影响[13-14]。
CHAI等[15]、XIA等[16]模拟研究并优化了带有扇形凹穴型微通道热沉及带有三角形凹穴型微通道热沉的结构,均认为凹穴作用能破坏微通道流动及传热边界层,从而强化微通道传热。SAN等[17]实验研究了肋间距比管道直径(p/d)、肋高比管道直径(e/d)及雷诺数对带有内肋微通道圆管的流动与传热影响,提出以p/d、e/d和雷诺数这3个参数为变量的努塞尔数(Nusslet,Nu)及摩擦系数关联式,用于指导工程应用。DHARAIVA等[18]详细分析了正弦结构粗糙元对微通道流动与传热的影响,分析其强化换热的原因是由于流动方向改变及面积增大导致的。ZHAI等[19]提出了扇形凹穴及内肋组合的复杂结构微通道热沉,用实验和模拟的方法研究其单相流动与传热的情况,结果表明,在雷诺数大于300时,其综合传热性能明显优于等截面微通道。因此,复杂结构微通道在传热方面具有明显优势。
合理的通道结构设计也可以改善传热效果。对于微通道而言,随着通道尺寸的降低,换热效果增强的同时压降也相应增加,因此传热效率和压降是衡量微通道综合传热性能的2个重要参数。工程设计一般都涉及多参数优化,称多目标参数优化[20-22]。LUO等[23]以肋高、凹穴直径、高及位置为变量,采用非支配排序遗传算法(NSGA-Ⅱ)以努塞尔数和摩擦系数为优化目标对带肋和凹穴通道进行结构优化。HUSAIN等[24-25]研究了变截面和带有粗糙元微通道热沉的流动与传热情况,用多目标遗传算法优化热阻及泵功2个目标函数,得到Pareto优化解集。SAMDA等[26]以通道高、凹穴间距及高为变量,对凹穴结构的微通道采用多目标遗传算法优化传热系数和压降。从理论上讲,遗传算法能从概率上随机寻找目标函数的最优解,比传统优化算法的适应性更强。
本文以圆形凹穴及内肋微通道为研究对象,首先用Fluent软件模拟不同结构参数的凹穴及内肋组合的微通道,构建热阻及泵功两个目标函数;然后,建立以微通道结构参数为变量的多目标遗传优化的数学模型。最后,用强化传热因子综合评价结构优化后通道的传热性能及分析通道内部流动与传热情况。
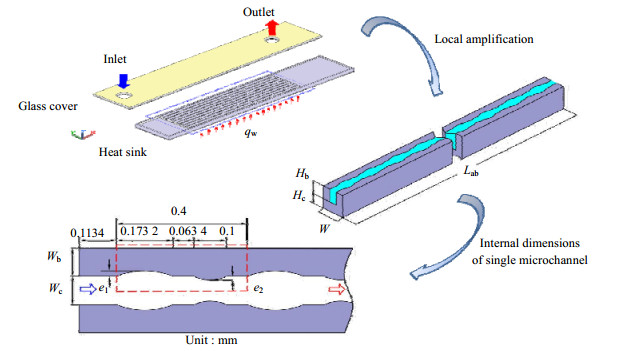
2 模型描述和方法 2.1 模型描述采用ZHAI等[27]提出的圆形凹穴及内肋微通道为参考通道,对其进行结构参数优化。图 1为圆形凹穴及内肋微通道的示意图。上层为玻璃盖板,通道层为硅基材料,流体采用上进上出的流动方式。加热段前设置了2.5 mm的绝热,可减缓流体从上而下流动时冲击射流造成扰动而使得进入各条通道的流量分配不均匀。热沉底座加热段由10条相同尺寸的圆形凹穴及内肋微通道组成,每条通道的长、宽、高分别为10、0.1和0.2 mm (如单通道局部放大图)。为模拟电子原件发热的情况,在加热段底部设置恒定热流密度为106 W·m-2作为发热源,加热面积为30 mm2。同时为了避免回流,在通道出口处设置长度为5 mm的绝热段。
|
图 1 圆形凹穴及内肋微通道示意图 Fig.1 Schematic of microchannel with circular cavities and internal ribs |
采用基于有限体积法的Fluent 18.0软件进行了数值模拟。稳态、层流及三维流动与传热过程的控制方程[28]如下:
| $\nabla \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {U} = 0$ | (1) |
| ${\rho _{\rm{f}}}{c_{{\rm{p,f}}}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {U} \cdot \nabla T = \nabla \cdot \left( {{\lambda _{\rm{f}}} \cdot \nabla T} \right)$ | (2) |
| ${\rho _{\rm{f}}}{c_{{\rm{p,f}}}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {U} \cdot \nabla T = \nabla \cdot \left( {{\lambda _{\rm{f}}} \cdot \nabla T} \right)$ | (3) |
式中:ρf,cp, f和λf为基于流体平均温度时的密度(kg·m-3)、比热(J·(kg·K)-1)和导热系数(W·(m·K)-1)。
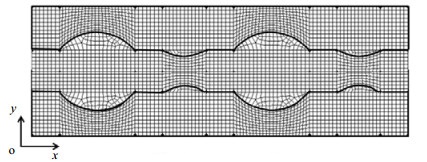
流体温度为293 K,入口速度为2 m·s-1。底面加热,热流密度为qw=106 W·m-2。通道两侧壁面为对称条件,用SIMPLEC算法求解上述方程,其收敛准则小于10-6。图 2为微通道网格划分图。如图 2所示,由于通道内肋区和凹穴区结构的复杂性,采用非均匀的结构网格划分,而在矩形区域采用结构化网格划分。在分析模拟结果之前,先对网格独立性及微通道单相层流流动与传热模型进行验证。
|
图 2 网格划分示意图 Fig.2 2D mesh structure of the microchannel |
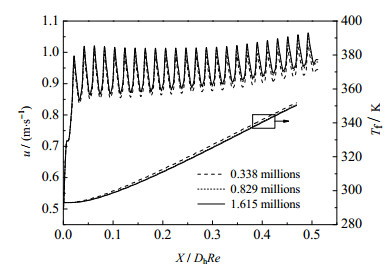
图 3为通道速度分布及流体温度分布沿流动方向无量纲长度的变化。选取通道尺寸为e1 = 0.01 mm,e2 = 0.011 3 mm进行检验,选取3种网格尺寸(33.8万、82.9万及161.5万)进行独立性检验,分别为33.8万(稀疏)网格、82.9万(较密)网格及161.5万(极密)网格。
从图 3可以看到,对比网格数82.9万(较密)和网格数161.5万(极密)的速度和温度值,其最大误差不超过1%和0.52%,说明当网格数为82.9万其结果已经很精确。但是使用33.8万网格来划分通道,其结果误差较大。因此,由于其他结构的通道尺寸变化不大,为了保证结果的准确性及节省计算时间,均按82.9万网格数来划分。
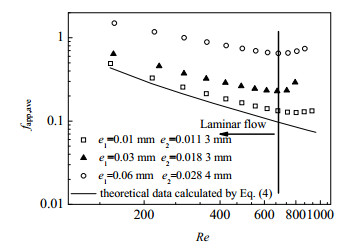
图 4为矩形微通道层流理论值与圆形凹穴及内肋微通道摩擦系数的对比。矩形微通道层流的摩擦系数由式(4)计算[29],而圆形凹穴及内肋微通道摩擦系数则根据模拟的压降值由式(5)计算:
|
图 3 网格独立性验证 Fig.3 Validation of gird independence |
|
图 4 层流模型验证 Fig.4 Validation of laminar flow model |
| ${f_{{\rm{app,ave}}}}Re = \sqrt {{{\left[ {\frac{{3.2}}{{{{{L_{{\rm{ab}}}}} / {\left( {{D_{\rm{h}}} \cdot Re} \right)}}}}} \right]}^2} + {{\left( {2fRe} \right)}^2}} $ | (4) |
式中:
| ${f_{\rm app,ave}} = \frac{{2\Delta p{D_\rm h}}}{{{\rho _\rm f}{L_{\rm ab}}u_{\rm in}^2}}$ | (5) |
式中:Δp为压降(Pa),Dh为通道水力直径(m),vc为通道宽高比,Lab为微通道长(mm),uin为入口速度(m·s-1)。
图 4为通道模拟的摩擦系数(散点)与由式(4)计算的理论层流摩擦系数(直线)的验证。由于凹穴高及内肋高的变化,在相同入口速度2 m·s-1时,雷诺数的变化范围为350~370。选取通道最大结构(e1=0.06 mm,e2=0.028 4 mm)和最小结构(e1=0.01 mm,e2=0.011 3 mm)分别对比,从图 4可以看到,当Re 700时,各模拟值的变化趋势与理论值一样,符合层流模型,但由于凹穴及内肋的存在,增大了流体内部的扰动,其压降均大于矩形微通道,因此摩擦系数也高于矩形微通道。但当Re > 700时,随着扰动继续增大,其流动已不再是层流。因此,此次模拟的通道结构入口速度选择为2 m·s-1,对应雷诺数变化范围为350~370,均符合层流范围。
3 多目标遗传优化理论以凹穴高e1及内肋高e2为变量,模拟30组不同结构参数的圆形凹穴及内肋微通道的流动与传热情况,其中凹穴高和肋高的变化范围分别为0.01 mm < e1 < 0.06 mm和0.01 mm < e2 < 0.03 mm。对于微通道而言,传热增强的同时压降也相应地增大。因此,为了得到通道最优传热性能,选择影响传热的热阻Rth和影响流动的泵功PP为目标函数,当热阻和泵功同时最小时,通道的综合传热性能最优。热阻和泵功分别采用式(6)、(7)计算:
| ${R_{{\rm{th}}}} = \frac{{{T_{{\rm{b,max}}}} - {T_{{\rm{in}}}}}}{Q} = \frac{{{T_{{\rm{b,max}}}} - {T_{{\rm{in}}}}}}{{{q_{\rm{w}}}{A_{\rm{b}}}}}$ | (6) |
| $PP = N{A_{{\rm{ch}}}}{u_{{\rm{in}}}}\Delta p$ | (7) |
式中:Tb, max和Tin分别为加热底面最大温度和通道入口流体温度,K;Q、qw和Ab分别为加热功率(W)、热流密度(W·m-2)和加热底面面积(m2)。N、Ach、uin分别为通道总数、单根通道横截面积(m2)、入口速度(m·s-1)。
在进行遗传算法优化前,首先根据模拟结果分别由式(6)、(7)计算得出热阻及泵功值,构建由变量(e1,e2)组成目标函数方程z=f (e1,e2),可以采用响应平面近似法(response surface methodology,RSM)来构建方程[30]。
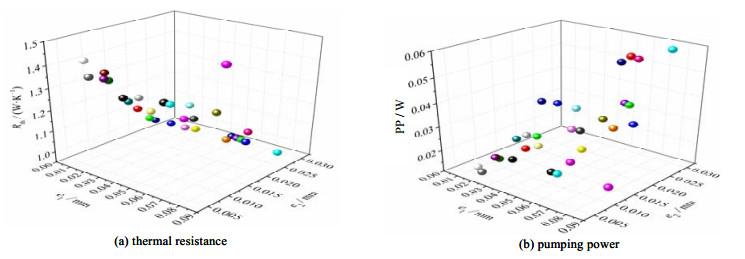
图 5为热阻及泵功随凹穴高及内肋高变化的散点图(由模拟结果计算得到)。根据热阻及泵功值的散点分布情况,分别在Origin软件里用多项式回归(Poly2D)和Logistic回归(LogisticCum)实现响应平面的构建。根据三维响应平面的形状,分别对式(8)、(9)采用非线性平面拟合:
|
图 5 热阻及泵功随凹穴高及内肋高变化的散点图 Fig.5 Distribution of thermal resistance and pumping power vs. height of cavities and ribs |
| ${R_{\rm th}}({e_1},{e_2}) = {a_0} + {a_1}{e_1} + {a_2}{e_2} + {a_3}e_1^2 + {a_4}{e_1}{e_2} + {a_5}e_2^2$ | (8) |
| $PP({e_1},{e_2}) = {b_0} + \frac{{{b_1}}}{{\left[ {1 + {{\exp }_{}}\left\{ {\left. {\frac{{{b_2} - {e_1}}}{{{b_3}}}} \right\}} \right.} \right]\left[ {1 + {{\exp }_{}}\left\{ {\left. {\frac{{{b_4} - {e_2}}}{{{b_5}}}} \right\}} \right.} \right]}}$ | (9) |
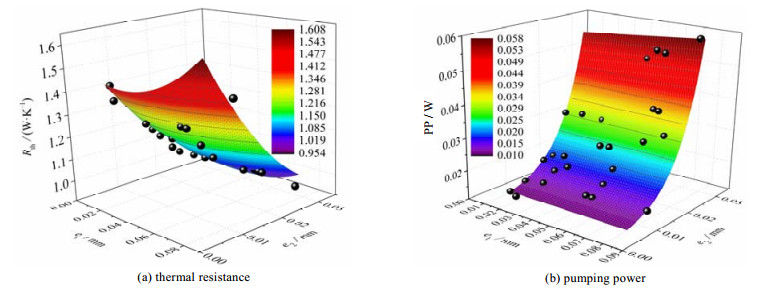
图 6为由拟合式(8)和(9)计算的热阻及泵功值随凹穴高及内肋高的变化情况。可以看到,计算值基本分布在曲面上,说明曲面能很好地反映出热阻和泵功散点值的分布情况。
|
图 6 热阻及泵功随凹穴高及内肋高变化的拟合公式曲面图 Fig.6 Respond surface graphs of thermal resistance and pumping power vs. height of cavities and ribs |
采用以下性能评价指标来评估热阻和泵功拟合方程的有效性:
均方根误差(root mean squared error,RMSE)
| ${\rm{RMSE}} = {(\frac{1}{t}{\sum\limits_{j = 1}^t {\left| {{P_j} - {Q_j}} \right|} ^2})^{1/2}}$ | (10) |
平均相对百分比误差(mean relative percentage error,MRPE)
| ${\rm{MRPE}} = \frac{{100\% }}{t}\sum\limits_{j = 1}^t {\left| {\frac{{{P_j} - {Q_j}}}{{{P_j}}}} \right|} $ | (11) |
误差平方和(sum of squared error,SSE)
| ${\rm{SSE}} = \sum\limits_{j = 1}^t {{{\left( {{P_j} - {Q_j}} \right)}^2}} $ | (12) |
多元统计系数(multivariate statistical coefficient,R2)
| ${R^2} = 1 - \frac{{\sum\limits_{j = 1}^t {{{\left( {{P_j} - {Q_j}} \right)}^2}} }}{{\sum\limits_{j = 1}^t {{{\left( {{P_j}} \right)}^2}} }}$ | (13) |
式中:P为实验值,Q为预测值,t为样本数目。其中,RMSE、MRPE及SSE越接近于0,R2越接近于1,说明模型的预测精度越高。表 1列举了热阻和泵功预测方程的性能评价指标。其中,热阻及泵功目标函数方程的多元统计系数R2分别为0.932 9及0.996 6。表 2为入口速度uin = 2 m·s-1时对应的目标函数的系数值。
|
|
表 1 热阻和泵功预测方程的性能评价指标 Table 1 Performance evaluation index of prediction equations of thermal resistance and pumping power |
|
|
表 2 目标函数的系数值 Table 2 Coefficients of objective functions |
以此目标函数为依据,建立微通道结构参数的多目标遗传优化的数学模型如下:
| $\begin{gathered} \min f({e_1},{e_2}) = \min \left\{ {{R_{{\rm{th}}}}({e_1},{e_2}),PP({e_1},{e_2})} \right\} \\ {\rm{s}}.{\rm{t}}.\begin{array}{*{20}{c}} {}&{}&{0.01 < } \end{array}{e_1} < 0.06\begin{array}{*{20}{c}} {}&{}&{}&{({\rm{unit}}:{\rm{mm}})} \end{array} \\ \begin{array}{*{20}{c}} {}&{}&{}&\begin{gathered} 0.01 < {e_2} < 0.03 \\ {u_{{\rm{in}}}} = {2_{}}m \cdot {s^{ - 1}}\begin{array}{*{20}{c}} {}&{} \end{array}Re = 350 \sim 370 \\ \end{gathered} \end{array} \\ \end{gathered} $ | (14) |
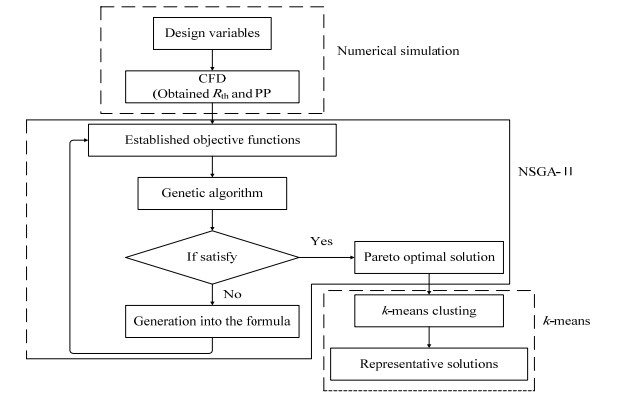
微通道结构优化的多目标遗传算法操作流程如图 7所示。
|
图 7 微通道结构优化的多目标遗传算法操作流程 Fig.7 Flowchart of multi-objective genetic algorithm operation for microchannel structural optimization |
如图所示,实现微通道结构优化的多目标遗传算法操作步骤分为3部分,第1步数值模拟,设计凹穴高e1和肋高e2的变量参数,由模拟结果计算热阻及泵功值;第2步为遗传操作过程,为了避免陷入局部最优解,分别设置迭代2000步的选择、交叉及变异的运算操作,交叉及变异概率分别设置为0.9和0.25,通过NSGA-Ⅱ算法运算得到最优解集——Pareto优化解集。第3步为采用k-means聚类法对最优解集进行4大聚类,最终得到4个代表性解。目标函数的构建、遗传算法的实现及k-means聚类法的操作均在Matlab软件里编程实现。
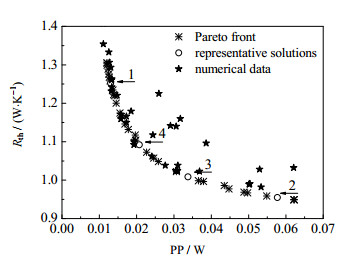
4 结果讨论与分析图 8为由多目标遗传算法得到的热阻及泵功的Pareto优化解集。其中,离散点为Pareto优化解集,1、2、3、4点为由k-means聚类法所得到的代表解。图 8表示在相同的泵功下,位于Pareto优化解集上的值为该结构下对应的最优热阻,可以看到大多数的模拟值(未优化前的结构)均不在优化解集上,说明这些结构都不是最优的。其中,工况1表示热阻较大,泵功较小的情况;工况2表示热阻较小,泵功较大的情况。因此,设计者可以根据图 8自行选择适应实际工况微通道的凹穴高及内肋高的组合。
|
图 8 热阻和泵功Pareto优化解集 Fig.8 Pareto front of thermal resistance and pumping power |
表 3为Pareto优化解中4个聚类点的变量参数及目标函数值与模拟值的对比。从表 3可以看到,热阻和泵功的理论值和模拟值的平均误差分别为2.06%和1.39%左右,吻合性较好。造成误差的原因是目标函数及遗传操作中交叉及变异概率的设置。
|
|
表 3 目标函数的Pareto优化值与模拟值的对比 Table 3 Comparison of Pareto front and numerical data |
由前面分析可知,通道传热性能强化的同时流动阻力也会增大,即热阻下降的同时泵功增大。因此,可采用强化传热因子η评价微通道强化后和强化前的综合传热性能,其计算式如下:
| $\eta = \left( {Nu/N{u_0}} \right)/{\left( {{f_{{\rm{app,ave }}}}/{f_{{\rm{app,ave 0}}}}} \right)^{1/3}}$ | (15) |
当η > 1时,说明在相同泵功下,强化后微通道的综合传热性能优于未强化的。0表示未优化前的通道,选取参考通道(e1=0.05 mm,e2=0.018 2 mm)。Nu公式为:
| $Nu = \frac{{h{D_{\rm{h}}}}}{{{\lambda _{\rm{f}}}}}$ | (16) |
| $h = \frac{Q}{{N{A_{{\rm{ch}}}}\Delta T}} = \frac{{{q_w}{A_{\rm{b}}}}}{{N{A_{{\rm{ch}}}}\left( {{T_{\rm{b}}} - {T_{\rm{f}}}} \right)}}$ | (17) |
式中:h为表面传热系数,W·(m2·K)-1,可由式(17)计算。Tb和Tf分别为加热底面平均温度和流体平均温度,K。
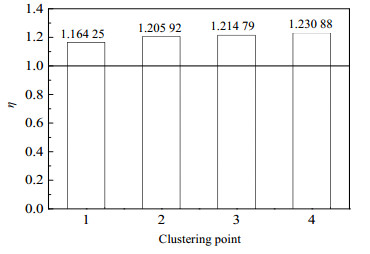
图 9为4个聚类点及未优化前的微通道的强化传热因子的对比。从图 9可知,4个聚类点对应通道结构的强化传热因子均大于1,说明优化后的微通道的强化传热效果优于未优化前的(e1=0.05 mm,e2=0.018 3 mm),其中点4的通道结构(e1=0.036 8 mm,e2=0.019 3 mm)对应的综合传热性能最优。对比图 8及图 9可知,图 8曲线前端及后端各工况的强化传热因子较小(如工况1及2),而中间段的强化传热因子较大(如工况3及4),说明热阻较大或泵功较大时其综合传热效果不如热阻及泵功较均匀时的工况。因此,多目标遗传算法可提供一定工况范围内的优化解集。
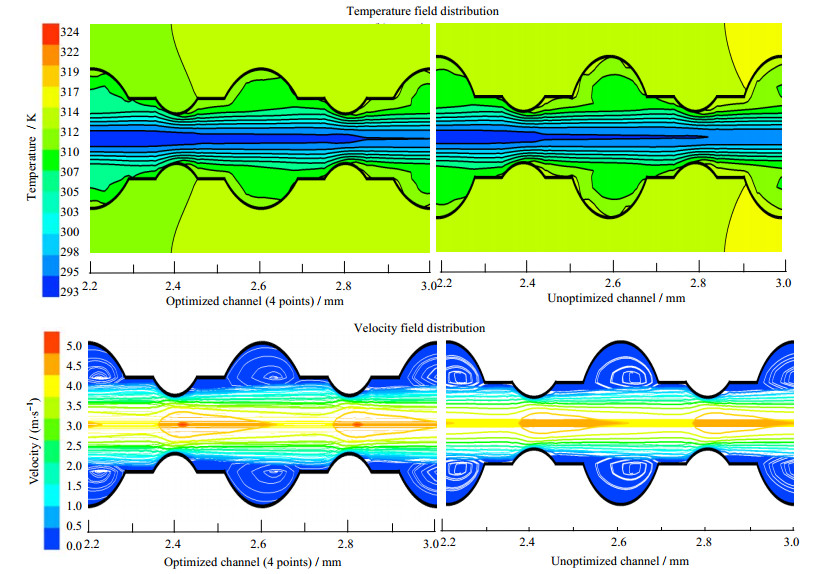
图 10为优化后4点对应结构的通道与未优化通道的温度场与速度场内部分布情况。从温度场看到,优化后的通道结构内流体中心温度高于未优化前的,且壁面温度更低,说明该通道的换热效果很好。原因可从速度场分布可知,在凹穴区由于面积增大速度下降形成涡旋;而在肋区流动边界层被肋高打断,流动区域变窄,速度加快,扰动增强,引起压损。总之,合理的结构布置使凹穴与内肋可以连续打断流动边界层、增强内部扰动、引起流动分离及产生旋涡,这些原因都促进通道的强化传热。
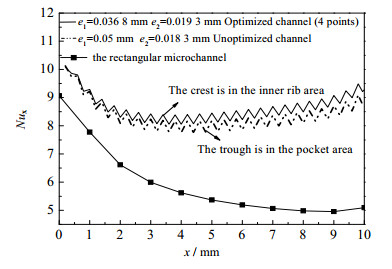
图 11为优化后4点对应的通道结构与未优化通道的Nux数随通道长度的分布情况。从图中可以看到,圆形凹穴与内肋微通道的Nux数随流动方向呈波动变化,其传热情况均优于相同尺寸的矩形微通道。曲线波谷处为凹穴区,其传热情况低于波峰处的内肋区,说明内肋对传热增强效果大于凹穴的。优化后的通道Nux数比未优化的增大了约27%。因此,合理的通道结构设计可以有效地提高传热性能。
|
图 9 强化传热因子对比 Fig.9 Comparison of thermal enhanced factor |
|
图 10 温度场和速度场对比 Fig.10 Comparison of temperature and velocity fields |
|
图 11 局部Nux数随流动方向的变化 Fig.11 Variation of local Nux number along flowing direction |
采用多目标遗传算法对圆形凹穴及内肋组合的微通道进行结构优化,利用Fluent 18.0对任意凹穴高及内肋高组合的30组微通道结构进行模拟,建立以微通道结构参数为变量的多目标遗传优化的数学模型,得到的主要结论如下:
(1) 采用响应平面近似法构建热阻及泵功的目标函数,其多元统计系数R2分别为0.932 9和0.996 6,说明函数精确度高。
(2) 设置迭代2 000步的选择、交叉及变异的运算操作,交叉及变异概率分别设置为0.9和0.25,通过NSGA-Ⅱ算法运算得到最优解集,用k-means聚类法对最优解集进行聚类,最终得到4个代表性解。
(3) 由强化传热因子分析可知,优化结构后的微通道综合传热性能高于未优化前的,说明合理的结构设计能使凹穴及内肋连续打断热边界层、增强内部扰动,使内部温度场分布更均匀。其中,热阻较大或泵功较大时的综合传热效果不如热阻及泵功较均匀时的工况,说明多目标遗传算法可提供一定工况范围内的优化解集。
|
|
符号说明: |
| [1] |
SARAFRAZ M M, SAFAEI M R, GOODARZI M, et al. Heat transfer analysis of Ga-In-Sn in compact heat exchanger equipped with straight micro-passages[J]. International Journal of Heat and Mass Transfer, 2019, 139: 675-684. DOI:10.1016/j.ijheatmasstransfer.2019.05.057 |
| [2] |
陈珉芮, 钱锦远, 李晓娟, 等. 十字形微通道中非定常分散相速度下液滴生成的数值分析[J]. 高校化学工程学报, 2018, 32(3): 522-528. CHEN M R, QIAN J Y, LI X J, et al. Numerical simulation of drop generation in cross-junction microchannel under changing dispersion phase velocities[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(3): 522-528. |
| [3] |
KEWALRAMANI G V, AGRAWAL A, SAHA S K. Modeling of microchannel heat sinks for electronic cooling applications using volume averaging approach[J]. International Journal of Heat and Mass Transfer, 2017, 115: 395-409. DOI:10.1016/j.ijheatmasstransfer.2017.08.041 |
| [4] |
CHU W X, CHEN C Y, LIAO Y H, et al. A novel micro-channel heat sink with trapezoid drainage for enhancing condensation heat transfer of dielectric fluid[J]. Experimental Thermal and Fluid Science, 2019, 106: 11-24. DOI:10.1016/j.expthermflusci.2019.04.023 |
| [5] |
SARAFRAZ M M, YANG B, POURMEHRAN O, et al. Fluid and heat transfer characteristics of aqueous graphene nanoplatelet (GNP) nanofluid in a microchannel[J]. International Communications in Heat and Mass Transfer, 2019, 107: 24-33. DOI:10.1016/j.icheatmasstransfer.2019.05.004 |
| [6] |
周云龙, 常赫. 壁面性质对蛇形微通道单状流传热特性的影响[J]. 高校化学工程学报, 2018, 32(6): 46-51. ZHOU Y L, CHANG H. Effects of wall properties on heat transfer characteristics of slug flow in serpentine microchannels[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(6): 46-51. |
| [7] |
AIFARVIAT A A, DOBROVICESCU A, STANCIU D. Influence of heat flux and Reynolds number on the entropy generation for different types of nanofluids in a hexagon microchannel heat sink[J]. Chinese Journal of Chemical Engineering, 2019, 27(3): 501-513. DOI:10.1016/j.cjche.2018.08.009 |
| [8] |
NAPHON P, WIRIYASART S, ARISARIYAWONG T, et al. ANN, numerical and experimental analysis on the jet impingement nanofluids flow and heat transfer characteristics in the micro-channel heat sink[J]. International Journal of Heat and Mass Transfer, 2019, 131: 329-340. DOI:10.1016/j.ijheatmasstransfer.2018.11.073 |
| [9] |
NAPHON P, NAKHARINTR L, WIRIYASART S. Continuous nanofluids jet impingement heat transfer and flow in a micro-channel heat sink[J]. International Journal of Heat and Mass Transfer, 2018, 126: 924-932. DOI:10.1016/j.ijheatmasstransfer.2018.05.101 |
| [10] |
DIXIT T, GHOSH I. Review of micro- and mini-channel heat sinks and heat exchangers for single phase fluids[J]. Renewable and Sustainable Energy Reviews, 2015, 41: 1298-1311. DOI:10.1016/j.rser.2014.09.024 |
| [11] |
XIA G D, CHAI L, ZHOU M Z, et al. Effects of structural parameters on fluid flow and heat transfer in a microchannel with aligned fan-shaped reentrant cavities[J]. International Journal of Thermal Sciences, 2011, 50(3): 411-419. DOI:10.1016/j.ijthermalsci.2010.08.009 |
| [12] |
XU J L, GAN Y H, ZHOU D C, et al. Microscale heat transfer enhancement using thermal boundary layer redeveloping concept[J]. International Journal of Heat and Mass Transfer, 2005, 48(9): 1662-1674. DOI:10.1016/j.ijheatmasstransfer.2004.12.008 |
| [13] |
翟玉玲, 夏国栋, 刘献飞, 等. 复杂结构微通道热沉液体强化传热过程的热力学分析[J]. 化工学报, 2014, 65(9): 3403-3409. ZHAI Y L, XIA G D, LIU X F, et al. Thermodynamic analysis of enhanced heat transfer process in microchannel heat sinks with complex structure[J]. CIESC Journal, 2014, 65(9): 3403-3409. |
| [14] |
RAHIMI-GORJI M, POURMEHRAN O, HATAMI M, et al. Statistical optimization of microchannel heat sink (MCHS) geometry cooled by different nanofluids using RSM analysis[J]. The European Physical Journal Plus, 2015, 130(2): 1-21. |
| [15] |
CHAI L, XIA G D, ZHOU M Z, et al. Numerical simulation of fluid flow and heat transfer in a microchannel heat sink with offset fan-shaped reentrant cavities in sidewall[J]. International Communications in Heat and Mass Transfer, 2011, 38(5): 577-584. DOI:10.1016/j.icheatmasstransfer.2010.12.037 |
| [16] |
XIA G D, ZHAI Y L, CUI Z Z. Numerical investigation of thermal enhancement in a micro heat sink with fan-shaped reentrant cavities and internal ribs[J]. Applied Thermal Engineering, 2013, 58(1/2): 52-60. |
| [17] |
SAN J Y, HUANG W C. Heat transfer enhancement of transverse ribs in circular tubes with consideration of entrance effect[J]. International Journal of Heat and Mass Transfer, 2006, 49(17): 2965-2971. |
| [18] |
DHARAIYA V V, KANDLIKAR S G. A numerical study on the effects of 2d structured sinusoidal elements on fluid flow and heat transfer at microscale[J]. International Journal of Heat and Mass Transfer, 2013, 57(1): 190-201. DOI:10.1016/j.ijheatmasstransfer.2012.10.004 |
| [19] |
ZHAI Y L, XIA G D, LIU X F, et al. Heat transfer enhancement of Al2O3-H2O nanofluids flowing through a micro heat sink with complex structure[J]. International Communications in Heat and Mass Transfer, 2015, 66: 158-166. DOI:10.1016/j.icheatmasstransfer.2015.05.025 |
| [20] |
LUO L, Du W, WANG S T, et al. Multi-objective optimization of a solar receiver considering both the dimple/protrusion depth and delta-winglet vortex generators[J]. Energy, 2017, 137: 1-19. DOI:10.1016/j.energy.2017.07.001 |
| [21] |
RAM K P, LAI S P, AHMEH M R. Design and optimization of airfoils and a 20 kW wind turbine using multi-objective genetic algorithm and HARP Opt code[J]. Renewable Energy, 2019, 144: 56-67. DOI:10.1016/j.renene.2018.08.040 |
| [22] |
PAUL D, SAHA S, MATHEW J. Fusion of evolvable genome structure and multi-objective optimization for subspace clustering[J]. Pattern Recognition, 2019, 95: 58-71. DOI:10.1016/j.patcog.2019.05.033 |
| [23] |
LUO L, DU W, WANG S T. Multi-objective optimization of the dimple/protrusion channel with pin fins for heat transfer enhancement[J]. International Journal of Numerical Methods for Heat and Fluid Flow, 2019, 29: 790-813. DOI:10.1108/HFF-05-2018-0194 |
| [24] |
HUSAIN A, KIM K Y. Multiobjective optimization of a microchannel heat sink using evolutionary algorithm[J]. Journal of Heat Transfer, 2008, 130(11): 114505. DOI:10.1115/1.2969261 |
| [25] |
HUSAIN A, LEE K D, KIM K Y. Enhanced multi-objective optimization of a dimpled channel through evolutionary algorithms and multiple surrogate methods[J]. International Journal for Numerical Methods in Fluids, 2011, 66: 742-759. DOI:10.1002/fld.2282 |
| [26] |
SAMAD A, LEE K D, KIM K Y. Multi-objective optimization of a dimpled channel for heat transfer augmentation[J]. Heat and Mass Transfer, 2008, 45: 207-217. DOI:10.1007/s00231-008-0420-6 |
| [27] |
ZHAI Y L, XIA G D, LIU X F, et al. Heat transfer in the microchannels with fan-shaped reentrant cavities and different ribs based on field synergy principle and entropy generation analysis[J]. International Journal of Heat and Mass Transfer, 2014, 68: 224-233. DOI:10.1016/j.ijheatmasstransfer.2013.08.086 |
| [28] |
YADAV V, BAGHEL K, KUMAR R, et al. Numerical investigation of heat transfer in extended surface microchannels[J]. International Journal of Heat and Mass Transfer, 2016, 93: 612-622. DOI:10.1016/j.ijheatmasstransfer.2015.10.023 |
| [29] |
HAN R K, LONDON A L. Laminar flow forced convection in ducts[M]. New York: Academic Press, 1978.
|
| [30] |
BADHURSHAH R, SAMAD A. Multi-objective optimization of a bidirectional impulse turbine[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2015, 229: 584-596. DOI:10.1177/0957650915589271 |




