2. 武汉市氢燃料电池工程技术研究中心,湖北 武汉 430064;
3. 清华大学 核能与新能源技术研究院,北京 100084
2. Wuhan Hydrogen Fuel Cell Engineering Research Center, Wuhan 430064, China;
3. Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing 100084, China
燃料电池发动机是一种利用电化学原理将燃料化学能直接转换为电能的发电装置,与传统热机相比,具有清洁环保、高效率、低噪音等显著优势[1-2],是未来车辆动力系统的重要发展方向之一。随着燃料电池的研发投入不断加大,燃料电池发动机的功率密度、寿命等性能指标不断提高,成本显著下降,已达到商业化示范阶段。然而,当前国产燃料电池发电机的可靠性较低,极大制约了燃料电池发动机的进一步推广使用。
燃料电池发动机工作时燃料(氢气)与氧化剂(空气)以设定的流量、压力、温度和相对湿度被通入至燃料电池的阳极和阴极,在电堆中以对应的操作电流和电压发生反应直接产生电能并排出生成反应产物水,同时生成的废热需要通过外部换热装置排出。工作环境参数变化区间大,功率需求工况复杂多变导致燃料电池发动机的系统复杂程度较高,导致对燃料电池发动机的故障诊断及可靠性分析较难[3]。
燃料电池发动机的可靠性分析和设计是系统设计过程中所不可缺少的环节,其目的是为了分析设备的各组成零部件与系统之间的可靠性关系,得出燃料电池发动机失效原因组合方式,指导发动机设计全过程,从而针对故障率较高的失效模式进行优化和改进,提升发动机系统运行的稳定性和可靠性[4]。因此使用科学方法对燃料电池发动机进行故障分析和风险评估势在必行[5]。
FMECA(failure mode effect and criticality analysis)是指失效模式影响及严重度分析,该方法通过分析系统中各个零部件的失效模式、对系统的影响及故障危害度,确定系统中各个单点故障对整个系统的影响。经过长期工程实践中的不断总结、修改和完善,最终形成了一套针对工程中不同故障模式的影响及故障严重度评价的分析方法[6]。FMECA能够较好地预防事故的发生,国内外大量学者利用FMECA方法对相关工业设备进行了故障模式、影响和危害性分析。JOMDE等[7]利用FMECA方法对制冷系统中的核心零部件往复式压缩机的7种失效模式进行了计算和分析,结果表明该方法可以被用于往复式压缩机的优化设计中。BRAHIM等[8]利用FMECA中信息在汽车行业中的案例研究,验证其在工业环境中的适用性。安颖等[9]利用FMECA方法对汽车CVT机械系统的部分失效模式进行了综合模糊评估,将系统各种失效模式用其危害度等级的方式描述出来。李海洋等[10]利用模糊FMECA方法对齿轮的制造工艺进行可靠性评价, 在获得各失效模式的危害度定量排序以后, 再将各失效模式作为影响因素对齿轮制造工艺进行二级模糊合评价。FMECA方法已经在军事工业、机械制造、汽车工业、电子设备等领域广泛应用,取得了丰富的研究成果。
目前已在工业实践中使用的风险系数法(risk priority number, RPN)即为其中一种较为成熟和通用的方法,该方法针对某一故障模式的3个方面,即:S-严重度、O-频度和D-探测度分别打分,最后将三者的分数相乘得到某一故障模式的RPN值,RPN值越高即代表该失效模式的危害程度越高。该方法具有简洁易操作的特性,尤其适宜于工程应用。但是,目前在燃料电池发动机的设计过程中,风险评估仍以主观定性描述为主,未引入影响因素权重,针对多种失效模式的综合分析仍有一定的局限性[11]。在以往的失效模式影响及严重度评价过程中,人们通常采用定性方式评价某种失效模式的若干方面,造成了评价结果的主观性,评价结果也难以重复和复现。
本文引入模糊数学方法,利用定量数值描述定性问题,使主观评价得以量化[12]。以某型燃料电池发动机为分析对象,将模糊数学方法引入燃料电池发动机系统的风险评估分析,利用模糊数学工具将FMECA的评价指标予以量化替代传统定性分析,避免了评价方法的主观性和随意性,为今后燃料电池发动机的设计与寿命评价提供了很好的参考。
2 FMECA法(失效模式影响及严重度分析)基本流程基于模糊数学的FMECA方法分为5个步骤:(1)建立因素集、评价集;(2)确定失效模式评价矩阵;(3)确定影响因素权重集;(4)完成一级模糊综合评价,获得各失效模式危害度大小;(5)完成综合危害等级确定及排序。评价方法流程如图 1所示。

|
图 1 FMECA综合评价流程图 Fig.1 Flowchart of failure mode effect and criticality analysis (FMECA) |
以某型燃料电池发动机为例,将基于模糊评价的FMECA法应用于该发动机的风险评估中。
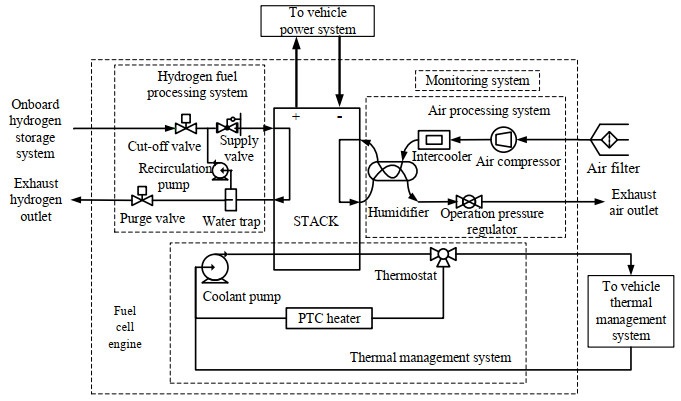
3 FMECA法在燃料电池发动机的实际应用 3.1 燃料电池发动机系统及典型失效模式燃料电池发动机主要由燃料电池电堆、供氢模块、供气模块、水热管理模块和监控模块5部分组成。发动机系统框图如图 2所示。
|
图 2 燃料电池发动机系统原理图 Fig.2 Schematic diagram of a fuel cell engine system |
根据工程实践和资料统计,选取燃料电池发动机具有代表性的9种典型失效模式,如表 1所示。
|
|
表 1 燃料电池发动机典型失效模式 Table 1 Typical failure modes of fuel cell engine systems |
因素集是影响评估系统的各元素的集合,因素集中不同元素代表不同的影响因素。针对燃料电池发动机的9种典型失效模式,结合实际情况定义了4种影响因素。燃料电池发动机的FMECA分析采用以下因素集:
| $ {U^k} = \left\{ {u_1^k\mathit{, }u_2^k\mathit{, }u_3^k\mathit{, }u_4^k} \right\} = \left\{ {失效频率, 严重度, 失效检测概率, 可维修性能} \right\} $ | (1) |
评价集是所有可取得的评价结果所组成的集合,用V表示,评价集中的各个元素代表评价结果的各个等级。针对燃料电池发动机,本文将评价结果分为4个等级,对应的评价集如下式,相对应等级划分如表 2所示。
|
|
表 2 评价集及等级划分 Table 2 Partition of factor set and evaluation set |
| $ \mathit{\boldsymbol{V}} = \left\{ {{v_1}, {v_2}, {v_3}, {v_4}} \right\} = \left\{ {1, 3, 5, 7} \right\} $ | (2) |
为建立燃料电池发动机典型失效模式的评价矩阵(本例中k = 9),成立了一个由d人(本例中d = 10)组成的专家组,各成员对上述4种影响因素评出一个且仅一个评价等级(本例中j = 4),确定第i种因素的评价集。在对第k个失效模式进行评价的过程中,设第i个影响因素uik的评价集为Rik,评价各影响因素对其因素水平集的隶属度。评价方法是成立一个由d人组成的专家组,各成员对各影响因素uik评出一个且仅一个评价等级vj,若d位成员中评定uik隶属于vj的有dijk人,则该评价集Rik为:
| $ \mathit{\boldsymbol{R}}_i^k = \left\{ {\frac{{d_{i1}^k}}{d}, \frac{{d_{i2}^k}}{d}, \cdots , \frac{{d_{im}^k}}{d}} \right\} = \left\{ {r_{i1}^k, r_{i2}^k, \cdots r_{im}^k} \right\}, 其中, \sum\limits_{j = 1}^m {\frac{{d_{ij}^k}}{d} = 1} $ | (3) |
将第k个失效模式的评价集写成失效模式k的水平评价矩阵Rk:
| $ {\mathit{\boldsymbol{R}}^k} = {[\mathit{\boldsymbol{R}}_1^k, \mathit{\boldsymbol{R}}_2^k, \cdots , \mathit{\boldsymbol{R}}_n^k]^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} {r_{11}^k}&{r_{12}^k}& \cdots &{r_{1m}^k}\\ {r_{21}^k}&{r_{22}^k}& \cdots &{r_{2m}^k}\\ \vdots & \vdots & \vdots & \vdots \\ {r_{n1}^k}&{r_{n1}^k}& \cdots &{r_{nm}^k} \end{array}} \right] $ | (4) |
在本文中,建立燃料电池发动机系统失效模式1:电堆氢气泄露的模糊评价矩阵。经综合评估,失效频率因素水平集为:
| $ {\mathit{\boldsymbol{R}}^1} = {[\mathit{\boldsymbol{R}}_1^1, \mathit{\boldsymbol{R}}_2^1, \mathit{\boldsymbol{R}}_3^1, \mathit{\boldsymbol{R}}_4^1]^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} {0.2}&{0.4}&{0.3}&{0.1}\\ 0&0&{0.2}&{0.8}\\ {0.4}&{0.4}&{0.2}&0\\ {0.1}&{0.1}&{0.4}&{0.4} \end{array}} \right] $ |
权重集是为反映各个影响因素重要程度而赋值相应权数所组成的集合。设权重值wik为第i元素对失效模式k影响程度的权数,根据工程实践定义因素权重集如下:
| $ {\mathit{\boldsymbol{W}}^k} = \left\{ {w_1^k, w_2^k, w_3^k, w_4^k} \right\} = \left\{ {0.2, 0.4, 0.2, 0.2} \right\} $ | (5) |
将第k个失效模式的因素权重向量Wk与失效模式k的水平评价矩阵Rk相乘得到失效模式 k的综合模糊评价向量Bk。
| $ {\mathit{\boldsymbol{B}}^k} = {\mathit{\boldsymbol{W}}^k} \cdot {\mathit{\boldsymbol{R}}^k} = \left[ {w_1^k, w_2^k, \cdots w_n^k} \right] \cdot \left[ {\begin{array}{*{20}{c}} {r_{11}^k}&{r_{11}^k}& \cdots &{r_{11}^k}\\ {r_{11}^k}&{r_{11}^k}& \cdots &{r_{11}^k}\\ \vdots & \vdots & \vdots & \vdots \\ {r_{11}^k}&{r_{11}^k}& \cdots &{r_{11}^k} \end{array}} \right] = \left[ {b_1^k, b_2^k, \cdots , b_m^k} \right] $ | (6) |
燃料电池发动机系统失效模式1的一级模糊评价B1为:
| $ {\mathit{\boldsymbol{B}}^1} = {\mathit{\boldsymbol{W}}^1} \cdot {\mathit{\boldsymbol{R}}^1} = \left[ {0.2, 0.4, 0.2, 0.2} \right] \cdot \left[ {\begin{array}{*{20}{c}} {0.2}&{0.4}&{0.3}&{0.1}\\ 0&0&{0.2}&{0.8}\\ {0.4}&{0.4}&{0.2}&0\\ {0.1}&{0.1}&{0.4}&{0.4} \end{array}} \right] = \left[ {0.13, 0.17, 0.24.0.46} \right] $ |
由计算结果可知:失效模式1对各个危害等级的隶属度为0.13、0.17、0.24和0.46。
3.7 综合危害等级计算计算失效模式k下的综合危害等级Ck为:
| $ {C^k} = {\mathit{\boldsymbol{B}}^k} \cdot {\mathit{\boldsymbol{V}}^{\rm{T}}} = \left[ {b_1^k, b_2^k, \cdots , b_m^k} \right] \cdot {\left[ {{v_1}, {v_2}, \cdots , {v_m}} \right]^{\rm{T}}} $ | (7) |
由上式可得失效模式1的综合危害等级C1为:
| $ {C^1} = {\mathit{\boldsymbol{B}}^1} \cdot {\mathit{\boldsymbol{V}}^{\rm{T}}} = \left[ {0.13, 0.17, 0.24, 0.46} \right] \cdot {\left[ {1, 3, 5, 7} \right]^{\rm{T}}} = 4.92 $ |
同理可得失效模式2至失效模式9的评价矩阵R2~R9分别为:
| $ \begin{array}{l} {\mathit{\boldsymbol{R}}^2} = \left[ {\begin{array}{*{20}{c}} {0.1}&{0.3}&{0.4}&{0.2}\\ 0&{0.1}&{0.6}&{0.3}\\ {0.8}&{0.2}&0&0\\ {0.7}&{0.2}&{0.1}&0 \end{array}} \right]\;{\mathit{\boldsymbol{R}}^3} = \left[ {\begin{array}{*{20}{c}} {0.4}&{0.3}&{0.2}&{0.1}\\ {0.1}&{0.2}&{0.5}&{0.2}\\ {0.9}&{0.1}&0&0\\ {0.2}&{0.7}&{0.1}&0 \end{array}} \right]\\ {\mathit{\boldsymbol{R}}^4} = \left[ {\begin{array}{*{20}{c}} {0.1}&{0.1}&{0.4}&{0.4}\\ {0.1}&{0.7}&{0.2}&0\\ {0.8}&{0.2}&0&0\\ {0.7}&{0.2}&{0.1}&0 \end{array}} \right]\;{\mathit{\boldsymbol{R}}^5} = \left[ {\begin{array}{*{20}{c}} {0.4}&{0.4}&{0.2}&0\\ {0.1}&{0.4}&{0.4}&{0.1}\\ {0.7}&{0.3}&0&0\\ {0.1}&{0.3}&{0.5}&{0.1} \end{array}} \right]\\ {\mathit{\boldsymbol{R}}^6} = \left[ {\begin{array}{*{20}{c}} {0.6}&{0.3}&{0.1}&0\\ {0.6}&{0.3}&{0.1}&0\\ {0.2}&{0.4}&{0.4}&0\\ {0.9}&{0.1}&0&0 \end{array}} \right]\;{\mathit{\boldsymbol{R}}^7} = \left[ {\begin{array}{*{20}{c}} {0.9}&{0.1}&0&0\\ {0.2}&{0.6}&{0.2}&0\\ {0.8}&{0.2}&0&0\\ {0.7}&{0.3}&0&0 \end{array}} \right]\\ {\mathit{\boldsymbol{R}}^8} = \left[ {\begin{array}{*{20}{c}} {0.1}&{0.1}&{0.4}&{0.4}\\ {0.9}&{0.1}&0&0\\ {0.9}&{0.1}&0&0\\ {0.1}&{0.2}&{0.6}&{0.1} \end{array}} \right]\;{\mathit{\boldsymbol{R}}^9} = \left[ {\begin{array}{*{20}{c}} {0.1}&{0.1}&{0.8}&0\\ {0.3}&{0.4}&{0.3}&0\\ {0.9}&{0.1}&0&0\\ {0.5}&{0.5}&0&0 \end{array}} \right] \end{array} $ |
同时依据式(6)计算得到失效模式2至失效模式9的一级模糊评价B2~B9分别为:
| $ \begin{array}{l} {\mathit{\boldsymbol{B}}^2} = \left[ {0.25.0.53, 0.39, 0.19} \right], {\mathit{\boldsymbol{B}}^3} = \left[ {0.34.0.3, 0.26, 0.1} \right], \\{\mathit{\boldsymbol{B}}^4} = \left[ {0.42.0.34, 0.16, 0.08} \right], {\mathit{\boldsymbol{B}}^5} = \left[ {0.28.0.36, 0.3, 0.06} \right], \\ {\mathit{\boldsymbol{B}}^6} = \left[ {0.58.0.28, 0.14, 0} \right], {\mathit{\boldsymbol{B}}^7} = \left[ {0.56.0.36, 0.08, 0} \right], \\{\mathit{\boldsymbol{B}}^8} = \left[ {0.58.0.12, 0.2, 0.1} \right], {\mathit{\boldsymbol{B}}^9} = \left[ {0.42.0.3, 0.28, 0} \right]。\end{array} $ |
至此最终得到上述各失效模式C1至C9的综合危害等级C为:
| $ C = \left\{ {{C^1}, {C^2}, {C^3}, {C^4}, {C^5}, {C^6}, {C^7}, {C^8}, {C^9}} \right\} = \left\{ {4.92, 4.76, 3.24, 2.8, 3.28, 2.12, 2.04, 2.64, 2.72} \right\} $ |
根据上述计算得到的各失效模式的综合危害等级,可以对该型燃料电池发动机系统的各典型失效模式的危害程度进行排序。9种失效模式对应的C值越大,表示该失效模式的风险最严重,依据模型计算结果,严重程度即:电堆氢气泄露 > 某片单电池电压低于下限 > 氢气入口压力不满足范围 > 电堆出口冷却水温度过高 > 管路系统软管破裂 > 巡检仪单片电压显示异常 > 氢气循环泵故障 > 空气入口压力不满足范围 > 电堆模块高功率工况下均一性差。表明在燃料电池发动机的设计初期,应该对危害程度高的失效模式进行针对性地改进。
4 结论本文将模糊数学方法引入燃料电池发动机系统的FMECA分析中,采用模糊数学工具和FMECA方法对燃料电池发动机系统的几种典型失效模式进行了计算分析和综合评价,并对其危害程度进行了排序。几种典型失效模式的危害程度排序结果与工程实践结果相符合,表明该方法在燃料电池发动机系统设计过程中及可靠性和失效模式影响分析中是适用的,在燃料电池发动机的设计初期,应该对危害程度高的失效模式进行针对性地改进。
应用FMECA法可以将燃料电池发动机的各故障模式进行定量评价,便于针对特定故障模式进行改进和优化设计,克服了以往的可靠性及严重度评价中主观因素大、可重复性差的弊端。在燃料电池发动机的实际开发过程中,可依据FMECA方法的标准流程对产品生命周期中出现的多种失效模式分别进行统计和评估,结合样本数据与统计学方法开展全面分析以指导提升产品的可靠性。
| [1] |
衣宝廉. 燃料电池-原理·技术×应用[M]. 北京: 化学工业出版社, 2003. YI B L. Fuel cell-Principle, technology and application[M]. Beijing: Chemical Industry Press, 2003. |
| [2] |
石锟, 冯磊, 姚力, 等. 金属双极板TiCr膜层氯离子腐蚀的研究与模拟[J]. 高校化学工程学报, 2019, 33(4): 843-848. SHI K, FENG L, YAO L, et al. Study and simulation on chloride ion corrosion of TiCr coated metallic bipolar plates[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(4): 843-848. |
| [3] |
王勇, 刘志祥. 质子交换膜燃料电池停机策略的实验研究[J]. 高校化学工程学报, 2016, 30(5): 1197-1202. WANG Y, LIU Z X. Experimental study on shutdown strategy of proton exchange membrane fuel cells[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(5): 1197-1202. |
| [4] |
甘传付, 曹宏炳, 黄允华, 等. 基于FMECA、FTA的故障诊断和故障预报[J]. 系统工程与电子技术, 2002, 24(11): 127-130. GAN C F, CAO H B, HUANG Y H, et al. FMECA and FTA based fault diagnosis and fault prognosis[J]. Systems Engineering and Electronics, 2002, 24(11): 127-130. |
| [5] |
庞志成, 王越. 燃料电池的进展及应用前景[J]. 化工进展, 2000, 19(3): 33-36. PANG Z C, WANG Y. Development and application prospect of fuel cell[J]. Chemical Industry and Engineering Progress, 2000, 19(3): 33-36. |
| [6] |
李君山, 屠庆慈, 陆廷孝. 计算机辅助FMECA与FTA综合分析[J]. 北京航空航天大学学报, 1992, 18(1): 38-43. LI J S, TU Q C, LU T X. Computer aided integrated FMECA and FTA[J]. Journal of Beijing University of Aeronautics and Astronautics, 1992, 18(1): 38-43. |
| [7] |
JOMDE A, BHOJWANI V, KEDIA S, et al. Failure modes effects and criticality analysis of the linear compressor[J]. Materials Today:Proceedings, 2017, 4(9): 10184-10188. |
| [8] |
BRAHIM I B, ADDOUCHE S A, MHAMEDI A E, et al. Build a Bayesian network from FMECA in the production of automotive parts:Diagnosis and prediction[J]. IFAC-PapersOnLine, 2019, 52(13): 2572-2577. |
| [9] |
安颖, 宋传学, 周云山, 等. 基于模糊评价法的FMECA在CVT可靠性分析中的应用[J]. 汽车技术, 2009(1): 6-9. AN Y, SONG C X, ZHOU Y S, et al. Application of FMECA in CVT reliability analysis based on fuzzy evaluation method[J]. Automobile Technology, 2009(1): 6-9. |
| [10] |
李海洋, 谢里阳, 张林林, 等. 基于模糊FMECA的齿轮制造工艺可靠性分析[J]. 机械设计, 2019, 36(1): 30-33. LI H Y, XIE L Y, ZHANG L L, et al. Analysis on the reliability of gear manufacturing process based on the fuzzy FMECA[J]. Journal of Machine Design, 2019, 36(1): 30-33. |
| [11] |
康锐, 石荣德. FMECA技术及其应用[M]. 北京: 国防工业出版社, 2006. KANG R, SHI R D. FMECA methodology and applications[M]. Beijing: National Defense Industry Press, 2006. |
| [12] |
RENJITH V R, KALATHIL J M, KUMAR P H, et al. Fuzzy FMECA (failure mode effect and criticality analysis) of LNG storage facility[J]. Journal of Loss Prevention in the Process Industries, 2018, 56: 537-547. |




