2. 浙江省化工高效制造技术重点实验室,浙江大学,浙江 杭州 310027
2. Zhejiang Provincial Key Laboratory of Advanced Chemical Engineering Manufacture Technology, Zhejiang University, Hangzhou 310027, China
釜式反应器因其混合效果好、传热传质效率高、操作灵活等优点,在石油化工、制药、冶金、食品、高分子、造纸、环保等领域有着广泛的应用[1]。强放热反应过程(如硝化反应、浓硫酸-双氧水体系中的氧化反应等)对反应釜的换热速率及温度控制有严格的要求,若温度控制不当,会引发反应体系中部分化合物分解,导致产生气体,进而恶化相关反应过程,甚至引发事故,但这些有气体产生的反应在某些行业仍得到较多应用,尤其广泛应用于国防工业中高性能含能化合物的制备过程。
在含能化合物的生产过程中,常采用轴向循环能力较强的推进桨和四斜叶桨[2],当搅拌釜夹套传热面积不能满足换热要求时,往往采用内置螺旋盘管来增加换热面积强化传热[3],但这也同时带来了计算和设计上的复杂。
目前,对气液搅拌釜内盘管外侧对流传热已有一定的研究。RAO和MURTI[4]用六叶涡轮搅拌器,在带有夹套无挡板的圆柱形搅拌釜内,以空气-水、空气-绝缘油、空气-润滑油作为传热介质,进行了一系列稳态传热实验;POLLARD和TOPIWALA[5]采用涡轮搅拌桨,以空气-水、空气-硫酸钾溶液作为传热介质,对单层和双层搅拌桨的气液两相体系进行了稳态传热研究;KURPIERS等[6-8]采用圆盘搅拌器对单相和多相体系的传热进行了较多的研究;RADEZ等[9]采用标准涡轮桨,在搅拌釜径分别为0.30和0.44 m并带有挡板的搅拌釜内,对通气和未通气情况下的传热进行了实验研究;DEMAERTELEIRE[10]采用四叶桨,对空气与6种不同牛顿流体构成的气液两相体系的盘管强制对流传热情况进行了实验研究,测定了气量对气液体系对流传热系数的影响,并关联得到方程:
| $N{u_c} = 3.18R{e^{0.627}}P{r^{0.342}}{\left( {\frac{\mu }{{{\mu _W}}}} \right)^{0.14}}W{e^{0.053}}F{r^{ - 0.156}}{\left( {\frac{{{V_s}}}{{dN}}} \right)^{0.079}}$ | (1) |
TRIVENI等[11]采用锚式搅拌桨和涡轮桨,应用牛顿流体和非牛顿流体,研究了在通气和未通气情况下盘管加热搅拌釜的传热,考察了搅拌雷诺数和通气量对对流传热的影响。但上述气液体系传热研究结果所采用的桨除了锚式搅拌桨以外均属于径向桨,轴向循环流较小,一般不适用于采用轴向桨的强放热反应过程,因此提出的通气量对传热影响的关联式无法直接应用到推进桨、四斜叶桨、翼型桨体系中,不利于对强放热反应器的放大及设计。
本文采用水和空气为工作介质,针对轴向推进桨、四斜叶桨、翼型桨作用下盘管外侧的对流传热系数进行实验研究,以考察桨径、气体流量、搅拌转速对盘管外侧对流传热的影响,并得出传热关联式,为相应的气液体系搅拌釜的工业设计和应用提供技术依据。
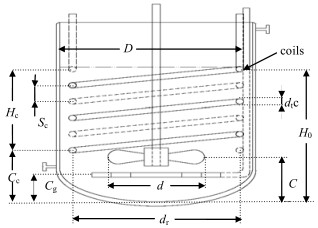
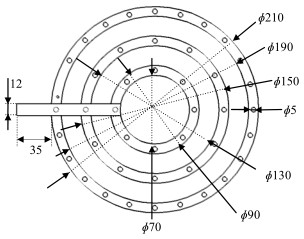
2 实验部分 2.1 实验装置采用底部为标准椭圆形封头的硼硅玻璃反应釜,无挡板,釜外设整体夹套,釜体采用厚度约为20 mm的保温棉保温,以避免热量损失。釜内装有螺旋盘管、气体分布器以及搅拌器。静止时液位高度H0 = D,搅拌装置如图 1所示。实验采用同心环气体分布器[12],如图 2所示。搅拌釜、螺旋盘管和气体分布器的详细信息见表 1。为考察桨型对盘管对流传热的影响,实验选取了推进桨(PRO)、四斜叶桨(PBT)和翼型桨(CBY) 3种形式的搅拌桨,离底高度均为C = 0.100 m,各搅拌桨直径见表 2。
|
图 1 搅拌釜示意图 Fig.1 Schematic diagram of the stirred tank |
|
图 2 同心环示意图 Fig.2 Schematic diagram of gas sparger concentric rings |
|
|
表 1 实验设备的几何特征 Table 1 Geometrical characteristics of the experimental equipment |
|
|
表 2 实验中所用搅拌桨的几何尺寸一览表 Table 2 Diameters of impellers used in the experiment |
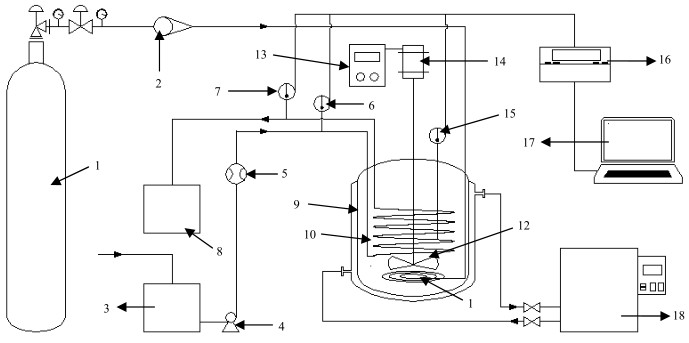
图 3为实验测试平台。气体从空气钢瓶流出,经过管道通过气体转子流量计进入气体分布器通入搅拌釜内。搅拌轴动力由三相异步电动机提供,采用数字变频仪控制搅拌轴转速。加热装置采用高温恒温槽,热水由高温恒温循环槽泵入夹套对釜内流体进行加热。冷却水由缓冲罐经循环泵打入盘管进水口,冷却釜内物料,冷却水流出盘管后进入回收罐。盘管冷却水流量由电磁流量计测得,盘管进出口温度和釜内流体的温度由铂电阻温度计测得,其精度为± 0.05 K,所有温度数据由数据采集卡采集并记录于电脑中。
|
图 3 对流传热实验装置示意图 Fig.3 Schematic diagram of the heat-transfer experimental setup 1. compressed air cylinder 2. gas rotameter 3 liquid storage tank 4 circulating pump 5 electromagnetic flowmeter 6, 7, 15 thermometer 8. recycle tank 9. stirred tank 10. coil 11. gas sparger 12. propeller 13. speed controller 14. agitator motor 16. digital acquisition system 17. computer 18. thermostatic bath |
实验采用非稳态法,主要包括以下实验步骤:安装气体分布器、盘管和搅拌桨,向搅拌釜内加入水使深度为H0 = D;开启高温恒温循环槽,向夹套内通入热水对搅拌釜内的液体进行加热;打开搅拌装置,用红外激光测速仪测量搅拌转速;待釜内温度升至337.15 K时,关闭高温恒温槽将夹套内的热水放空;打开数据采集系统对釜温Tr、盘管进水口Tin温度和盘管出水口温度Tout进行采集;调节气体阀门,通过气体流量计计量通气速率;以恒定流量(G = 0.0968 kg·s-1)向盘管通冷却水,待釜内温度降至303.15 K以下时,关闭冷却水循环泵,停止数据采集;重复上述步骤,直至完成其它工况的测定。
2.3 盘管外侧对流传热系数的计算方法忽略热量损失,釜内热量仅通过盘管的冷却水带出,非稳态冷却过程的能量衡算可以描述为[3, 13-17]:
| $m{C_{\rm{p}}}\frac{{{\rm{d}}{T_{\rm{r}}}}}{{{\rm{d}}t}} = KA({T_{\rm{c}}} - {T_{\rm{r}}})$ | (2) |
| $GC{'_{\rm{p}}}({T_{{\rm{out}}}} - {T_{{\rm{in}}}}) = KA({T_{\rm{r}}} - {T_{\rm{c}}})$ | (3) |
因
| $\ln \left( {{T}_{\text{r}}}-{{T}_{\text{in}}} \right)=\frac{-2KAGC_{\text{p}}^{'}}{m{{C}_{\text{p}}}\left( KA+2GC_{\text{p}}^{'} \right)}t+C$ | (4) |
实验测得Tr,Tin与时间t的关系,将Tr与Tin之差的自然对数对时间t作图,设冷却曲线的斜率为k,那么搅拌釜的总传热系数K为:
| $K = \frac{{ - 2m{C_{\rm{p}}}kG}}{{\left( {2G + mk} \right)A}}$ | (5) |
通过Wilson图法获得盘管外侧对流传热系数[18-19]:
| $\frac{1}{K} = \frac{1}{{{\alpha _{\rm{o}}}}} + \frac{1}{\varphi }$ | (6) |
其中,盘管外侧对流传热系数αo与搅拌转速N的关系一般为[11, 13]:
| $\frac{1}{{{\alpha _{\rm{o}}}}} = f\left( {{N^{ - 2/3}}} \right)$ | (7) |
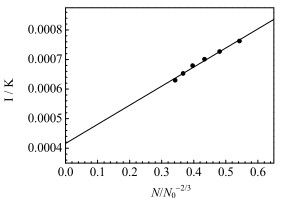
1/φ表示设备热阻,为装置常数,其值可通过Wilson图获得:以总传热系数的倒数为纵轴,以相对转速(参考搅拌桨速度N0为1 r·min-1)为横轴作出Wilson图,所得纵轴截距即为1/φ。PRO_L的Wilson图如图 4所示,图中的实验点基本落在一条直线上,线性关系较好,说明采用Wilson图法是可行的,从工程角度看基于Wilson图所得的相关结果也是较可靠的。通气情况下的实验原理与上面类似,由于所用设备一致,采用不通气下实验所得的设备传热热阻1/φ[11],因此可以通过式(8)计算盘管外侧对流传热系数αo:
| ${\alpha _{\rm{o}}} = \frac{1}{{{K^{ - 1}} - {\varphi ^{ - 1}}}}$ | (8) |
|
图 4 PRO_L的Wilson图 Fig.4 Wilson plot of PRO_L |
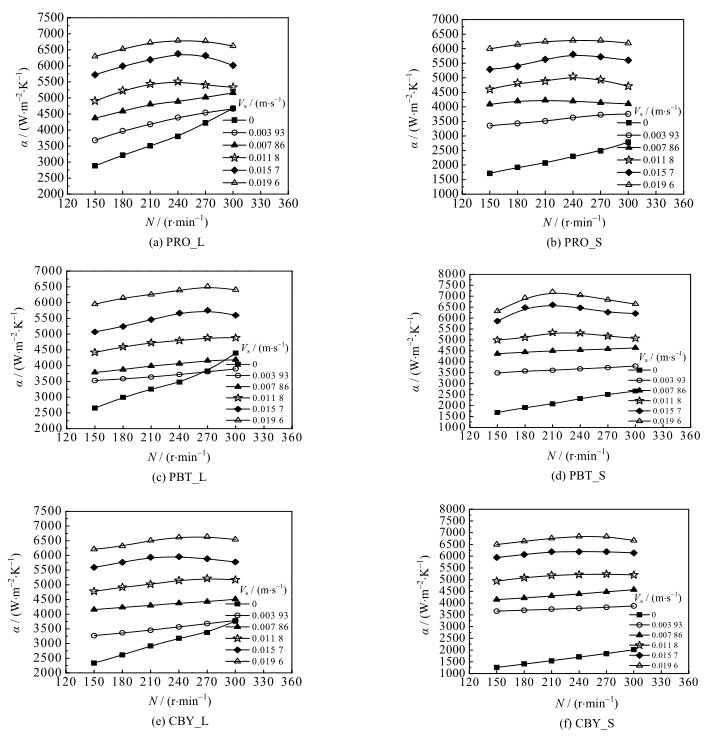
图 5为转速对管外对流传热系数的影响。由图可见,在不通气下,对流传热系数随转速的增大而增大。通气后,对流传热系数随搅拌转速的增大可能变大也可能变小:在低转速下,管外对流传热系数随转速的增大而增大,而在较高的通气速率和高搅拌转速下,反而随着转速的增大而减小,这与人们认为转速增大螺旋盘管外侧的对流传热将得到强化不同。POLLARD等[5]认为在低转速下,对流传热系数值增大,在高转速下其值不变。李永成等[20]在研究鼓泡塔中气液两相流与浸没在其中的垂直列管间的传热时发现,当通气速度大于0.1 m·s-1时,其提供的能量不但引起微漩涡的形成,促进传热,而且还用于产生对传热没有什么贡献的整体循环。可认为在搅拌釜内同样也会存在产生这种不利于传热的整体循环的现象,降低传热能力。另一方面,因为气体的比热容和导热系数较液体小得多,通入气体使盘管周围含有一定体积的气体,从而降低釜内盘管外侧的传热,且釜内气体含量越多,对传热的影响越显著,这与本实验在较高转速240、270、300 r·min-1下的规律相同,推测对于每一个表观气速,都存在一个这样的临界转速,当转速小于该临界转速时,对流传热系数随转速的增大而增大,当转速超过该临界转速时,反而随转速的增大而减小。因此当通气速率一定时,通过增加搅拌转速来强化传热要特别小心。
|
图 5 转速对管外对流传热系数的影响 Fig.5 Effects of rotation speeds on external coil heat transfer coefficients |
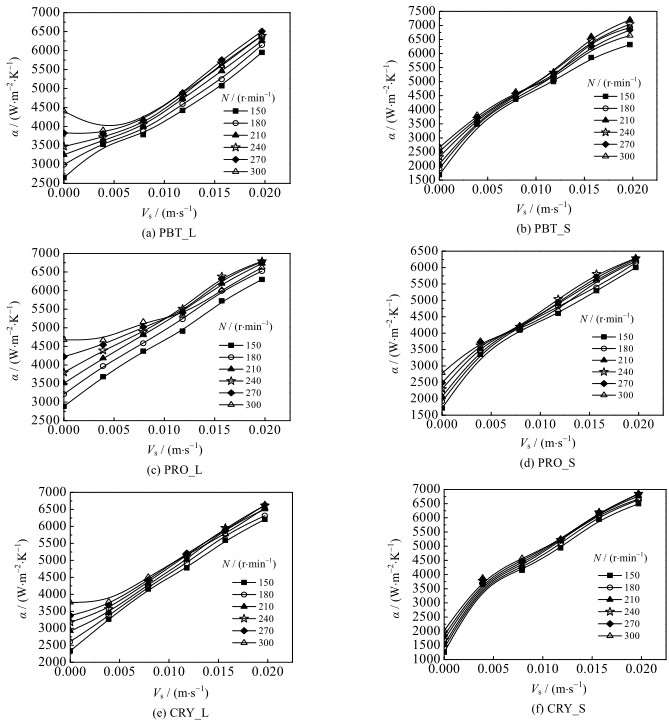
图 6为表观气速对盘管外侧对流传热的影响。
|
图 6 表观气速对管外对流传热系数的影响 Fig.6 Effects of superficial gas velocities on external coil heat transfer coefficients |
由图 6可见,总体而言,管外侧对流传热系数随表观气速的增加而增加。DEMAERTELEIRE[10]认为,气体的通入和分散使液体产生二次循环流,增大了整个体系的湍流强度,从而增强传热。此外,除了气体自身的搅拌作用和搅拌桨的机械搅拌作用外,气体在一定程度上冲刷螺旋盘管,热膜厚度减小,也能够更好地增强盘管和釜壁之间区域的流动,流动相对较弱的区域减少,因此可有效提高对流传热。RADEZ等[9]和KURPIERS等[6-8]则认为,通气后部分气泡附着在换热面上,热阻增大使传热系数减小;只有当气速很大时,传热系数才增大。本实验的表观气速在RADEZ等[9]实验范围(0~0.14 m·s-1),大部分工况的结果却是通气量增加管外对流传热增大,这与RADEZ[9]不利于传热的结论相反,与DEMAERTELEIRE[10]所认为的增强传热相同。与RADEZ等[9]结论相反的主要原因是搅拌转速的不同,其均在高转速(400~700 r·min-1)下所得的结果,而本实验转速为150~300 r·min-1;对比PRO_L、PBT_L和CBY_L可以看出,在转速为300 r·min-1,表观气速为0.003 93 m·s-1 (对应QG为1 m3·h-1)时管外对流传热系数要小于不通气情况,这和RADEZ等[9]所认为的气体的加入不利于传热的相同。
3.3 实验结果关联多相流动是一种比较复杂的流体运动形式,目前还没有很成熟的认识,WALLIS[21]称其为“不确定(insecure)科学”。本文采用类似DEMAERTELEIRE [10]的方法进行关联,并用通气准数NA = QG/(Nd3)代替DEMAERTELEIRE[10]文中的无因次数Vs/(dN),它们两者之间的关系为:
| ${N_{\rm{A}}}{\rm{ = }}\frac{{\pi {D^2}}}{{4{d^2}}} \times \frac{{{V_{\rm{s}}}}}{{dN}}$ | (9) |
关联传热系数时,DEMAERTELEIRE [10]考虑了Weber数的影响。Weber数代表惯性力和表面张力效应的比值。Weber数越小代表表面张力越重要,如毛细管现象,一般当Weber数远大于1时,表面张力便可以忽略。本实验过程中Weber数为90~1 216,表面张力的作用可以忽略。因此同其他学者一样,关联时不考虑表面张力这个因素。
通常,在搅拌釜内的流体处于湍流时,根据对流传热理论,对对流传热系数进行关联时,Pr的指数约等于1/3[22],Re的指数较接近2/3[23-24]。鉴于本文非稳态法的实验误差相对较大,为减少实验误差对关联式的影响,本文取Pr的指数为0.33,Re的指数为0.67。
对桨径为D/2和D/3的搅拌桨作用下盘管外侧对流传热系数进行拟合,引入通气准数得到各桨作用下盘管外侧对流传热系数的关联式:
推进桨:
| $ Nu = 1.18R{e^{0.67}}P{r^{0.33}}{(\frac{\mu }{{{\mu _{\rm{w}}}}})^{0.14}}F{r^{ - 0.12}}{N_{\rm{A}}}^{0.32} $ | (10) |
四斜叶桨:
| $ Nu = 1.67R{e^{0.67}}P{r^{0.33}}{(\frac{\mu }{{{\mu _{\rm{w}}}}})^{0.14}}F{r^{ - 0.081}}{N_{\rm{A}}}^{0.46} $ | (11) |
翼型桨:
| $ Nu = 1.54R{e^{0.67}}P{r^{0.33}}{(\frac{\mu }{{{\mu _{\rm{w}}}}})^{0.14}}F{r^{ - 0.093}}{N_{\rm{A}}}^{0.42} $ | (12) |
其中,0.016 5 ≤ NA ≤ 0.556,41 000 ≤ Re ≤ 185 000。
推进桨拟合结果的平均相对偏差为3.76%,最大相对偏差为13.4%;四斜叶桨拟合结果的平均相对偏差为6.31%,最大相对偏差为19.7%;翼型桨拟合结果的平均相对偏差为3.89%,最大相对偏差为11.7%。
通气准数NA表示通气量和搅拌转速以及桨径之间的相互作用关系,NA的指数越大,表明气速对该桨型的影响越强,在这3种轴向桨中,通入气体对推进桨的影响最小,对四斜叶桨的影响最大,对翼型桨的影响其次。RAO和MURTI[4]采用六叶涡轮搅拌器,其气速的指数约为0.64,DEMAERTELEIRE[10]采用四叶桨,所得相关气速的无因次(Vs/(dN))指数为0.079,李永成[20]在对鼓泡塔中气液两相流与浸没在其中的水平管间的传热研究发现,在Vs<0.1 m·s-1,传热系数与表观气速的0.25次方成正比,可认为通气指数0.32、0.46、0.42是在合理的范围内。
雷诺数Re的指数值与RAO和MURTI[4]、DEMAERTELEIRE[10]、TRIVENI[11]提出的指数相差很小,与常见的搅拌釜内传热关联式所得指数相同,这进一步支持了DEMAERTELEIRE[10]曾推测的一个观点:在气液传热体系中桨型对搅拌雷诺数的指数没有影响。
费劳德准数Fr对对流传热系数有着一定的影响,它表征流体惯性力和重力相对大小。推进桨、四斜叶桨和翼型桨指数值分别为0.12、0.081、0.093,较RAO和MURTI[4]和DEMAERTELEIRE[10]所得结果0.10相差不大,但是同TRIVENI[11]所得结果0.16差别较大。
需指出的是,鉴于本文采用非稳态法进行实验,并应用Wilson图法瞬态分离管外对流传热系数,忽略了材料的蓄放热的影响,且整体釜内汽液两相流也被集总参数处理,故相对而言存在较大的误差,因此要注意关联式(10)~(12)的适用范围和可靠性。建议尽量采用图 5的实验数据进行内插,若采用关联式(10)~(12)进行估算,则计算传热面积时工程余量要放得大一些。
4 结论本文以水和空气为介质,使用非稳态法,考察了桨径为D/3和D/2的推进桨、四斜叶桨、翼型桨作用下气液搅拌釜内盘管外侧的对流传热系数,得出以下结论:
(1) 当搅拌桨转速较低时,通入气体显著增强釜内流体的湍动程度,使管外对流传热系数大于不通气所得值;当搅拌桨转速较高时,釜内流体混合情况已较好,气体的搅拌作用的相对减弱,对传热的增强有所减弱。在较高通气量和较高转速下,随着转速的增加,管外对流传热系数反而有所减小,这一方面是因为搅拌釜内存在不利于传热的整体循环的现象,另一方面是因为气体的比热容和导热系数远小于液体,从而降低降低釜内盘管外侧的传热。
(2) 引入通气准数,关联得到了通气情况下推进桨、四斜叶桨和翼型桨型作用下盘管外侧对流传热系数的无因次关联式,其平均相对偏差分别为3.76%、6.31%和3.89%。
| 符号说明: | |||
| A | -盘管外侧传热面积,m2 | Re | -雷诺数,Re = d2Nρ·μ-1 |
| Cp | -釜内液体比热,J·kg-1·K-1 | Tc | -盘管内液体温度,K |
| Cp' | -盘管内液体比热,J·kg-1·K-1 | Tin | -盘管内液体进口温度,K |
| D | -釜内径,m | Tout | -盘管内液体出口温度,K |
| d | -搅拌桨直径,m | Tr | -釜内液体温度,K |
| Fr | -费劳德准数,Fr = dN2·g-1 | t | -时间,s |
| G | -盘管内液体质量流速,kg·s-1 | V | -釜内液体体积,m3 |
| g | -重力加速度,m·s-2 | Vs | -表观气速,m·s-1 |
| H0 | -不通气情况下搅拌釜内液面高度,m | We | -韦伯数,We = d3N2ρ·σ-1 |
| K | -盘管总传热系数,W·m-2·K-1 | αo | -盘管外侧对流传热系数,W·m-2·K-1 |
| m | -釜内液体质量,kg | ρ | -液体密度,kg·m-3 |
| N | -转速,r·min-1 | μ | -液体在主体温度下的黏度,Pa·s |
| NA | -通气数,NA= QG ·(d3N)-1 | μw | -液体在盘管壁面温度下的黏度,Pa·s |
| Nu | -努塞尔数,Nu = αoD·λ-1 | λ | -液体在主体温度下的导热系数,W·m-1·K-1 |
| Pr | -普朗特数,Pr = Cpμ·λ-1 | σ | -表面张力,kg·s-2 |
| QG | -通气量,m3·h-1 | ||
| [1] |
厉鹏, 刘宝庆, 金志江, 等. 搅拌釜内流场实验研究与数值模拟的进展[J]. 化工机械, 2010, 37(6): 799-822. LI P, LIU B Q, JIN Z J. Progress of the experimental researches and numerical simulations of the flow fields in stirred tanks[J]. Chemical Engineering & Machinery, 2010, 37(6): 799-822. DOI:10.3969/j.issn.0254-6094.2010.06.036 |
| [2] |
周俊超.含能化合物制备过程的相关基础问题研究[D].杭州: 浙江大学, 2013. ZHOU J C. Some fundamental problems in the process of the energetic compound preparation[D]. Hangzhou: Zhejiang University, 2013. |
| [3] |
JAIMES R, NUNHEZ J R. Obtaining the nusselt equation with the use of CFD for a stirred tank heated with helical coils[J]. Chemical Engineering Transactions, 2015, 43: 1687-1692. |
| [4] |
RAO K B, MURTI P S. Heat transfer in mechanically agitated gas-liquid systems[J]. Industrial & Engineering Chemistry Process Design and Development, 1973, 12(2): 190-197. DOI:10.1021/i260046a011 |
| [5] |
POLLARD R, TOPIWALA H H. Heat transfer coefficients and two-phase dispersion properties in a stirred-tank fermentor[J]. Biotechnology and Bioengineering, 1976, 18(11): 1517-1535. DOI:10.1002/bit.260181104 |
| [6] |
KURPIERS P, STEIFF A, Weinspach P M. Heat transfer in stirred multiphase systems[J]. Chemie Ingenieur Technik, 1984, 56(3): 234-235. DOI:10.1002/cite.330560315 |
| [7] |
KURPIERS P, STEIFF A, WEINSPACH P M. Heat-transfer and scale-up of agitated single and multiphase reactors with immersed heating elements[J]. Chemie Ingenieur Technik, 1985, 57(7): 632-633. DOI:10.1002/cite.330570718 |
| [8] |
KURPIERS P, STEIFF A, WEINSPACH P M. Heat-transfer between reactor wall and fluid in a stirred singlephase and multiphase reactor on use of one-stage and 2-stage disk stirrers[J]. Chemie Ingenieur Technik, 1985, 57(8): 700-701. DOI:10.1002/cite.330570815 |
| [9] |
RADEZ I, HUDCOVA V, KOLOINI T. Heat transfer in aerated and nonaerated mycelial fermentation systems in stirred tank reactors[J]. Chemical Engineering Journal and the Biochemical Engineering Journal, 1991, 46(3): B83-B91. DOI:10.1016/0300-9467(91)87009-y |
| [10] |
DEMAERTELEIRE E. Heat transfer to a helical cooling coil in mechanically agitated gas-liquid dispersions[J]. Chemical Engineering Science, 1978, 33(8): 1107-1113. DOI:10.1016/0009-2509(78)85016-7 |
| [11] |
TRIVENI B, VISHWANADHAM B, VENKATESHWAR S. Studies on heat transfer to Newtonian and non-Newtonian fluids in agitated vessel[J]. Heat and Mass Transfer, 2008, 44(11): 1281-1288. DOI:10.1007/s00231-007-0364-2 |
| [12] |
徐世艾, 韩晓丽, 冯连芳, 等. 气液固三相体系搅拌混合研究[J]. 化学工业与工程, 2000, 17(5): 278-286. XU S A, HAN X L, FENG L F, et al. Progress on stirred mixing of gas-liquid-particle three-phase system[J]. Chemical Industry and Engineering, 2000, 17(5): 278-286. DOI:10.3969/j.issn.1004-9533.2000.05.007 |
| [13] |
车圆圆, 周俊超, 毕纪葛, 等. 改进CBY桨搅拌釜内单相流体流动与传热特性研究[J]. 高校化学工程学报, 2014, 28(3): 489-496. CHE Y Y, ZHOU J C, BI J G, et al. Study on single phase fluid flow and heat-transfer performance in a stirred tank with an improved CBY hydrofoil Impeller[J]. Journal of Chemical Engineering of Chinese Universities, 2014, 28(3): 489-496. DOI:10.3969/j.issn.1003-9015.2014.05.14.02 |
| [14] |
STOESSEL F. Thermal safety of chemical process:Risk assessment and process design[M]. Beijing: Science Press, 2009.
|
| [15] |
BOUME J R, BUERLI M, Regenass W. Heat transfer and power measurements in stirred tanks using heat flow calorimetry[J]. Chemical Engineering Science, 1981, 36(2): 347-354. DOI:10.1016/0009-2509(81)85014-2 |
| [16] |
WILSON E E. A basis for rational design of heat transfer apparatus[J]. Transaction of the American Society of Mechanical Engineers, 1915, 37(1): 47-53. |
| [17] |
毕纪葛, 潘万贵, 周俊超, 等. 四斜叶桨搅拌下釜内盘管非稳态对流传热过程的模拟和实验研究[J]. 高校化学工程学报, 2015, 29(4): 780-788. BI J G, PAN W G, ZHOU J C, et al. CFD simulation and experimental study of heat transfer in a stirred tank equipped with a pitched-blade turbine and helical coils[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(4): 780-788. DOI:10.3969/j.issn.1003-9015.2015.06.25.05 |
| [18] |
FEMÁNDEZ-SEARA J, UHÍA F J, SIERES J, et al. A general review of the Wilson plot method and its modifications to determine convection coefficients in heat exchange devices[J]. Applied Thermal Engineering, 2007, 27(17/18): 2745-2757. |
| [19] |
DEBAB A, CHERGUI N, BEKRENTCHIR K, et al. An investigation of heat transfer in a mechanically agitated vessel[J]. Journal of Applied Fluid Mechanics, 2011, 4(2): 43-50. |
| [20] |
李永成, 刘长厚, 沈自求, 等. 垂直管中气液两相流传热研究[J]. 工程热物理, 1989, 10(1): 72-74. LI Y C, LIU C H, SHEN Z Q, et al. Heat transfer in bubble column and gas-lift loop reactors[J]. Journal of Engineering Thermophysics, 1989, 10(1): 72-74. |
| [21] |
WALLIS G B. Review-theoretical models of gas-liquid flows[J]. Journal of Fluids Engineering, 1982, 104(3): 279-283. DOI:10.1115/1.3241833 |
| [22] |
STROZZI F, ALOS M A, ZALDIVAR J M. A method for assessing thermal stability of batch reactors by sensitivity calculation based on Lyapunov exponents:Experimental verification[J]. Chemical Engineering Science, 1994, 49(24): 5549-5561. DOI:10.1016/0009-2509(94)00302-5 |
| [23] |
ALOS M A, STROZZI F, ZALDIVAR J M. A new method for assessing the thermal stability of semibatch processes based on Lyapunov exponents[J]. Chemical Engineering Science, 1996, 51(11): 3089-3094. DOI:10.1016/0009-2509(96)00202-3 |
| [24] |
ZALDIVAR J M, CANO J, ALOS M A, et al. A general criterion to define runaway limits in chemical reactors[J]. Journal of Loss Prevention in the Process Industries, 2003, 16(3): 187-200. DOI:10.1016/S0950-4230(03)00003-2 |




