2. 西安交通大学 能源与动力学院,陕西 西安 710049
2. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
时至今日,我国依然是以煤炭为主要一次能源的国家[1-3],煤炭清洁高效利用的重要性与日俱增[4-5]。水煤浆气化技术已经成为我国重要的煤炭清洁利用技术[6-7]。随着水煤浆气化技术应用和推广,很多国内外学者研究了提高其气化效率的方法,夏德宏等[8]在1992年提出,在水煤浆进入气化炉前对其预热,适当提高入口温度,可以提高水煤浆雾化效果和气化效率。KATAYAMA[9]也提出水煤浆的预热蒸发可以提高冷煤气效率,降低氧气消耗,但是水煤浆预热设备的研究还较少。NOVACK等[10]尝试开发了一种水煤浆预热蒸发装置,水煤浆在管内被加热,但是发现40%~60%质量分数的水煤浆会堵塞加热管。AIUCHI等[11]设计制造了一个水煤浆预热蒸发装置,利用很高的流速防止水煤浆在管内堵塞,但压降很大。
旋梯式螺旋折流板换热器是一种新形式的螺旋折流板换热器,其折流板连接布置示意图如图 1所示,折流板由一块平板弯折两次形成,组装后的两块折流板紧密接触。该板型的换热器不仅继承了螺旋折流板换热器壳侧阻力小、传热系数高以及有效抑制污垢沉积等优点[12-15],并且封堵了螺旋折流板换热器的三角漏流区。WEN等[16]采用数值方法研究了该换热器结构参数对其综合性能的影响,发现随着折弯度的减小,综合性能增强,随切割百分数的减小,综合性能先增强后减弱,随折弯角的增大,综合性能先增强然后减弱。WEN等[17]又进一步对该换热器进行了油-水单相实验研究,发现其综合性能相比普通螺旋折流板换热器平均提高19.5%。

|
图 1 旋梯式螺旋折流板连接布置示意图 Fig.1 Schematic diagram of the connection method of ladder-type fold baffles |
目前有关水煤浆流动研究多集中在水煤浆在管段中的流动。孟令杰[18]研究了水煤浆管内流动的相似准则数及阻力特性,提出采用广义雷诺数计算其层流流动的沿程能量损失系数。陈良勇等[19-20]研究了水煤浆浓度,粒径和温度对入口段的影响。任远等[21]研究了水煤浆流经渐缩管段的局部阻力特性,提出了水煤浆流经渐缩管段时局部阻力系数的准则式。目前还没有关于水煤浆在管壳式换热器壳侧流动的研究。
在换热器设计时通常将黏度大,难以产生较大传热膜系数的流体布置在壳侧[22-23]。考虑到水煤浆黏度大,容易堵塞的特点,若在管侧流动,易堵塞换热管且较高黏度的流体在管侧很难产生较大的传热膜系数,同时黏稠易沉积的水煤浆也不适用采用内螺纹管,管内插件等管侧传热强化措施[24-25]。而安排水煤浆在壳侧流动可以避免水煤浆堵塞换热管,同时壳侧错列排布的管束、折流板等都利于提高流体雷诺数,使流体达到湍流,利于介质传热[26]。很多强化壳侧传热的方式例如改变挡板结构,改变管束支撑结构等[27-29]都可以在后续的研究和工业中加以采用。结合旋梯式螺旋折流板换热器壳程可以产生交错的螺旋流等相应优点,本文将研究在壳侧预热水煤浆的可行性以及导热油定性温度、水煤浆体积流量对换热器流动换热性能的影响。同时考虑到还没有水煤浆在换热器壳侧的相关流动传热的研究,本文将采用较低质量分数的水煤浆(w = 19.5%),其实验数据对进一步开展更高浓度水煤浆的预热研究打下了重要基础,对水煤浆预热的工况选择和水煤浆预热换热器的设计具有指导意义。
2 实验系统和实验数据处理方法 2.1 实验元件本实验所用的旋梯式螺旋折流板换热器为壳程数为1,管程数为2的1-2型浮头型换热器。换热器的壳体尺寸为Φ273 mm×10 mm,换热管采用无缝钢管,换热管有效管长2 500 mm,换热管尺寸为Φ19 mm×2 mm,共40根,采用正方形排列,管间距为25 mm。换热器的一个螺距为115.8 mm,换热器的折流板之间采用拉杆和定距杆固定,拉杆尺寸为Φ12 mm,6根,定距杆为Φ23 mm×4 mm。图 2为实验采用的旋梯式螺旋折流板换热器实物图。

|
图 2 实验用换热器 Fig.2 Heat exchanger used in the study |
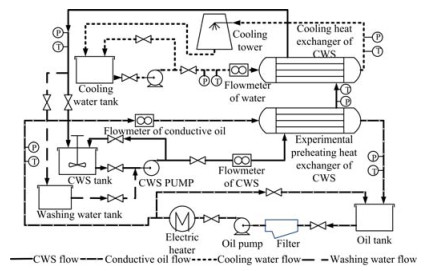
实验主要研究在不同的导热油定性温度下,水煤浆流量与水煤浆温升、壳侧压降、总传热系数的关系。实验系统流程示意见图 3,主要由水煤浆路循环、油路循环和冷却水循环3个循环以及数据采集记录系统组成。L-QC310导热油被一台150 kW电加热器加热后作为实验换热器的热流体,走管侧,流量可以手动调节。水煤浆储槽内的水煤浆经泵送后依次流过实验换热器壳侧和冷却换热器壳侧,在实验换热器中被加热,在冷却换热器被冷却,其流量可以手动调节。冷却水作为冷却换热器内的冷流体,走管侧。图 4为实验系统布置图。
|
图 3 实验系统流程图 Fig.3 Schematic diagram of the experimental process |

|
图 4 实验系统布置图 Fig.4 Picture of the experiment table arrangement |
实验系统中的水煤浆泵是型号G50-1的单螺杆泵,导热油泵是型号RY 60-45-200的风冷热油泵,冷却水泵是型号IS65-50-160的离心清水泵。数据采用Agilent 34972A采集,主要测量参数为导热油、水煤浆流量,实验换热器的壳侧、管侧进出口温度,壳侧总压降,测试仪表规格和精度见表 1。
|
|
表 1 测量仪表规格和精度 Table 1 Specification and accuracy of measuring instruments |
实验过程中,导热油流量维持在28 m3·h-1左右,壳侧水煤浆流量从8到18 m3·h-1逐渐增大,壳侧流量每变化2 m3·h-1取一个数据点。壳侧流量变化完一个周期后,提高导热油定性温度继续实验,依次完成导热油定性温度约为60、80和90 ℃时的实验数据测量。为了保证实验结果的可靠,每次在改变导热油定性温度或水煤浆体积流量后,均让系统维持运行一段时间,待流动传热稳定之后才开始采集数据,同时实时计算传热系数及热平衡偏差,当热平衡偏差小于±5%才进行下一组测量。
2.3 实验数据处理方法本文中总传热系数K的计算:
| $K = \frac{Q}{{A \times \Delta {t_{\rm{m}}}}}$ | (1) |
式中:K为总传热系数,W·m-2·K-1;Q为换热器的总换热量,W;A为换热器换热面积,m2;Δtm为对数平均温差,K。
考虑到冷流体得到的热量与热流体失去的热量不能达到绝对的相等,总换热量按下式求取:
| $Q = \frac{{{Q_{\rm{s}}} + {Q_{\rm{t}}}}}{2}$ | (2) |
| ${Q_{\rm{s}}} = {M_{\rm{s}}} \times {c_{p{\rm{s}}}} \times \left( {{t_{{\rm{s, out}}}} - {t_{{\rm{s, in}}}}} \right)$ | (3) |
| ${Q_{\rm{t}}} = {M_{\rm{t}}} \times {c_{p{\rm{t}}}} \times \left( {{t_{{\rm{t, in}}}} - {t_{{\rm{t, out}}}}} \right)$ | (4) |
式中:M为流体质量流量,kg·s-1;cp为定压比热容,J·kg-1·K-1。
换热面积计算式为:
| $A = N \times {\rm{ \mathsf{ π} }} \times {d_{\rm{o}}} \times L$ | (5) |
式中:N为换热管数;do为换热管外径,m;L为换热管有效长度,m。
对数平均温差按下式计算:
| $\Delta {t_{\rm{m}}} = \psi {\left( {\Delta {t_{\rm{m}}}} \right)_{{\rm{ctf}}}}$ | (6) |
| ${\left( {\Delta {t_{\rm{m}}}} \right)_{{\rm{ctf}}}} = \frac{{\Delta {t_{{\rm{max}}}} - \Delta {t_{{\rm{min}}}}}}{{{\rm{ln}}\left( {\Delta {t_{{\rm{max}}}}/\Delta {t_{{\rm{min}}}}} \right)}}$ | (7) |
| $\Delta {t_{{\rm{max}}}} = {t_{{\rm{t, in}}}} - {t_{{\rm{s, out}}}}$ | (8) |
| $\Delta {t_{{\rm{min}}}} = {t_{{\rm{t, out}}}} - {t_{{\rm{s, in}}}}$ | (9) |
式中:ψ为对数平均温差修正因子;Δtmax为最大温差,K;Δtmin为最小温差,K。下角标s、t分别表示壳侧、管侧,下角标in、out分别表示进出口。
壳侧传热膜系数hs由热阻分离法求得,本实验采用的换热器系首次使用,忽略管壁和污垢热阻,即:
| $ {h_{\rm{s}}} = 1/(\frac{1}{K} - \frac{{{d_{\rm{o}}}}}{{{h_{\rm{t}}}{d_{\rm{i}}}}}) $ | (10) |
式中:di为换热管内径,m;ht为管侧传热膜系数,W·m-2·K-1;由Dittus-Boelter公式[30]计算:
| $ {h_{\rm{t}}} = 0.023Re_{\rm{t}}^{0.8}Pr_{\rm{t}}^{{\rm{0}}{\rm{.3}}} \cdot \frac{{{k_{\rm{t}}}}}{{{d_{\rm{i}}}}} $ | (11) |
该关联式适用104≤Ret≤1.2×105,0.7≤Prt≤120,L/d≥60的情况,Ret为管侧雷诺数,Prt为管侧普朗特数,kt为管侧导热油的导热系数,W·m-1·K-1。
若Ret≤104,ht按下式计算[23]:
| $ {h_{\rm{t}}} = 0.023\phi Re_{\rm{t}}^{0.8}Pr_{\rm{t}}^{{\rm{0}}{\rm{.3}}} \cdot \frac{{{k_{\rm{t}}}}}{{{d_{\rm{i}}}}} $ | (12) |
ϕ为校正因子:
| $ \phi = 1 - \frac{{6 \times {{10}^5}}}{{Re_{\rm{t}}^{1.8}}} $ | (13) |
壳侧努赛尔数Nus和阻力系数fs由下式计算:
| $ N{u_{\rm{s}}} = \frac{{{h_{\rm{s}}}{d_{\rm{o}}}}}{{{k_{\rm{s}}}}} $ | (14) |
| $ {f_{\rm{s}}} = \frac{{2\Delta P}}{{\rho {u^2}}} \cdot \frac{B}{L} $ | (15) |
式中:ks为水煤浆的导热系数,W·m-1·K-1;ΔP为壳侧压降,Pa;B为折流板螺距,m。
本文水煤浆剪切力与剪切速率的的关系符合宾汉模型[31],即:
| $\tau = {\tau _0} + {\eta _{\rm{p}}}\gamma $ | (16) |
式中:τ为某一剪切速率下的剪切力,Pa;τ0为屈服应力,Pa;ηp为塑性黏度,Pa·s;γ为剪切速率,s-1。
表观黏度η为剪切力与剪切速率的比值,由下式计算:
| $ \eta = \frac{{{\tau _0}}}{\gamma } + {\eta _{\rm{p}}} $ | (17) |
水煤浆符合宾汉流体,引入宾汉雷诺数ReB,ReB和水煤浆的普朗特数Prs由下式计算:
| $ R{e_B} = \frac{{\rho u{d_{\rm{o}}}}}{{{\eta _{\rm{p}}}}} $ | (18) |
| $ P{r_{\rm{s}}} = \frac{{{c_{p{\rm{s}}}}{\eta _{\rm{p}}}}}{{{k_{\rm{s}}}}} $ | (19) |
式中:ρ为水煤浆密度,kg·m-3;cps是水煤浆定压比热容,J·kg-1·K-1;u为壳侧最小流通截面的流速,m·s-1。
| $ u = \frac{V}{{{A_{\rm{m}}}}} $ | (20) |
| $ {A_{\rm{m}}} = 0.5B\left[ {{D_{\rm{i}}} - {D_{\rm{l}}} + \frac{{\left( {{D_{\rm{l}}} - {d_{\rm{o}}}} \right)\left( {{t_{\rm{p}}} - {d_{\rm{o}}}} \right)}}{{{t_{\rm{p}}}}}} \right] $ | (21) |
式中:V为壳侧水煤浆体积流量,m3·s-1;Am为换热器壳侧最小流通截面积,m2;B为折流板螺距,m;Di为换热器内径,m;Dl为管束外切圆直径,m;tp为换热管间距,m。
2.4 实验不确定度分析根据文献[32-33]中关于计算绝对不确定度和相对不确定的方法,本实验的不确定度按下式计算:
| $ {U_R} = \sqrt {{{\left( {\frac{{\partial f}}{{\partial {x_1}}}} \right)}^2}U_{{x_1}}^2 + {{\left( {\frac{{\partial f}}{{\partial {x_2}}}} \right)}^2}U_{{x_2}}^2 + \cdot \cdot \cdot + {{\left( {\frac{{\partial f}}{{\partial {x_n}}}} \right)}^2}U_{{x_n}}^2} $ | (22) |
| $ {W_R} = {U_R}/R $ | (23) |
式中:R=f (x1, x2, x3, ···, xn)为间接测量量,而x1, x2, x3, ···, xn是直接测量量,UR为变量R的绝对不确定度,WR是变量R的相对不确定度。
计算得出,在本次实验的各个工况下,水煤浆温升ΔT、壳侧压降ΔP、壳侧单位压降温升ΔT/ΔP、总传热系数K、单位压降总传热系数K/ΔP、壳侧努赛尔数Nus和壳侧阻力系数fs的相对不确定度分别不大于5.50%、4.26%、5.59%、3.36%、4.87%、3.60%和6.85%。
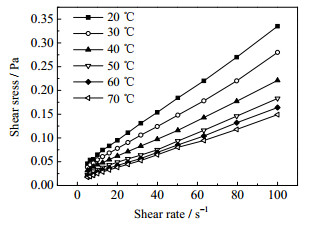
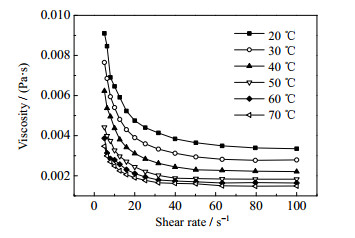
3 实验结果与分析 3.1 水煤浆流变性水煤浆流变特性由马尔文公司生产的Anton Paar MCR302可视化流变仪测量,图 5和图 6为不同温度下剪切力和表观黏度随剪切速率的变化关系。
|
图 5 不同温度下剪切力随剪切速率关系 Fig.5 Shear stress as a function of shear rate under different temperatures |
|
图 6 不同温度下表观黏度随剪切速率关系 Fig.6 Apparent viscosity as a function of shear rate under different temperatures |
基于流变实验数据,得到了水煤浆在不同温度下宾汉模型关系式,如表 2所示。
|
|
表 2 不同温度下的宾汉模型参数 Table 2 Bingham parameters under different temperature |
根据ROH等[34]的研究,水煤浆的流变模型与温度的关系符合Arrhenius方程,即:
| $\tau = \tau \left( \gamma \right)H\left( {{T_{{\rm{cws}}}}} \right) = \tau \left( \gamma \right){A_1}{\rm{exp}}\left( {\frac{{{E_{\rm{a}}}}}{{R{T_{{\rm{cws}}}}}}} \right)$ | (24) |
式中:Tcws为水煤浆的绝对温度,K;A1为一常数;Ea为活化能,J·mol-1;R是气体常数,8.314 J·mol-1·K-1。
考虑温度的影响,20~70 ℃的水煤浆的宾汉模型可以拟合为:
| $ \tau = \left( {6.08 \times {{10}^{ - 5}} + 5.78 \times {{10}^{ - 6}}\gamma } \right){\rm{exp}}\left( {\frac{{1\;835.2}}{{{T_{{\rm{cws}}}}}}} \right) $ | (25) |
式(25)的校正决定系数Adj.R2为0.996,与实验数据符合较好。相应的,本文中水煤浆的表观黏度可以按下式计算:
| $ \eta = \left( {\frac{{6.08 \times {{10}^{ - 5}}}}{\gamma } + 5.78 \times {{10}^{ - {\rm{6}}}}} \right)\exp \left( {\frac{{1\;835.2}}{{{T_{{\rm{cws}}}}}}} \right) $ | (26) |
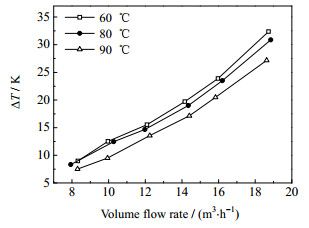
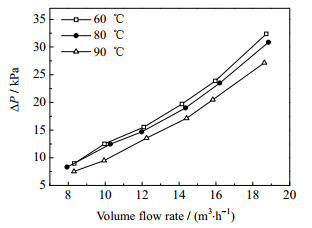
图 7和图 8示出不同导热油定性温度下水煤浆温升和壳侧压降随壳侧体积流量的关系。在某一导热油定性温度下,水煤浆温升随体积流量的增大而降低。同时,当导热油的定性温度增加时,被加热的水煤浆可以达到更大的温升。当导热油的定性温度约为80和90 ℃时,相比导热油的定性温度约为60 ℃,水煤浆温升分别提高了71.65%~77.90%和113.95%~120.45%。在某一导热油定性温度下,壳侧压降随体积流量的增大而逐渐增大,并且在体积流量较大时,壳侧压降增加更快。同时,当导热油的定性温度增加时,壳侧压降减小。当导热油的定性温度约为80和90 ℃时,相比导热油的定性温度约为60 ℃,壳侧压降分别降低了1.74%~5.65%和13.01%~23.82%。这是因为在导热油的定性温度较高时,相应的水煤浆的定性温度也较高,如图 9所示。而在一定温度范围内,水煤浆的黏度随其温度的升高而降低,其黏度随温度的下降关系可以由图 6和式(26)明显看到。所以提高导热油的定性温度可以降低壳侧压降。
|
图 7 不同导热油定性温度下水煤浆温升随流量关系 Fig.7 CWS temperature difference as a function of shell side flow rate under different oil reference temperatures |
|
图 8 不同导热油定性温度下壳侧压降随流量关系 Fig.8 Shell side pressure drop as a function of shell side flow rate under different oil reference temperatures |

|
图 9 不同导热油定性温度下水煤浆定性温度随流量关系 Fig.9 CWS reference temperature as a function of shell side flow rate under different oil reference temperatures |
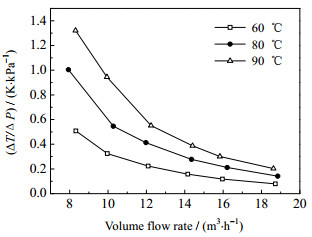
图 10为不同导热油定性温度下的壳侧单位压降温升,可以看到,壳侧单位压降温升随体积流量的增大而逐渐减小。同时,较高导热油定性温度下的壳侧单位压降温升明显高于较低导热油定性温度下的值。当导热油的定性温度约为80和90 ℃时,相比导热油的定性温度约为60 ℃,壳侧单位压降温升分别提高了80.92%~87.16%和148.92%~189.00%。
|
图 10 不同导热油定性温度下壳侧单位压降温升随流量关系 Fig.10 Shell side temperature difference per unit pressure drop as a function of shell side flow rate under different oil reference temperatures |
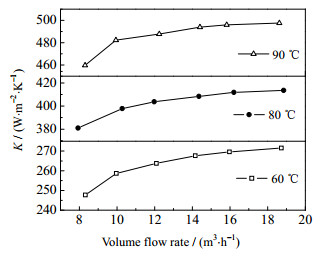
图 11为不同导热油定性温度下总传热系数随壳侧体积流量的变化关系,在某一导热油定性温度下,总传热系数随体积流量的增大而逐渐增大,但增大速率随水煤浆体积流量的增加而减小。而当导热油的定性温度更高时,总传热系数更大。当导热油的定性温度约为80和90 ℃时,相比导热油的定性温度约为60 ℃,总传热系数分别提高了52.25%~54.90%和83.26%~86.46%。这是因为在导热油的定性温度更高时,导热油和水煤浆的黏度都有所下降,管侧和壳侧的雷诺数因而都相应增加,增强了传热能力。
|
图 11 不同导热油定性温度下总传热系数随流量关系 Fig.11 Overall heat transfer coefficient as a function of shell side flow rate under different oil reference temperatures |
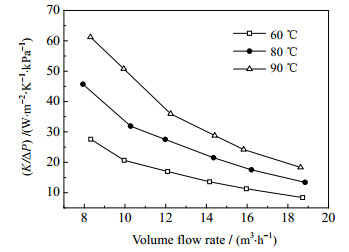
图 12示出不同导热油定性温度下壳侧单位压降总传热系数随壳侧体积流量的变化关系,可以看到,较高导热油定性温度下的壳侧单位压降总传热系数明显高于较低导热油定性温度下的值。当导热油的定性温度约为80和90 ℃时,相比导热油的定性温度约为60 ℃,壳侧单位压降总传热系数分别提高了59.88%~63.31%和111.09%~144.63%。
|
图 12 不同导热油定性温度下壳侧单位压降总传热系数随流量关系 Fig.12 Overall heat transfer coefficient per unit shell side pressure drop as a function of shell side flow rate under different oil reference temperatures |
外部强制对流传热的壳侧传热实验关联式和阻力系数实验关联式一般采用如下形式[35-37]:
| $ N{u_{\rm{s}}} = {C_1}Re_{\rm{B}}^{{m_1}}Pr_{\rm{s}}^{1/3} $ | (27) |
| $ {f_{\rm{s}}} = {C_2}Re_{\rm{B}}^{{m_2}} $ | (28) |
式中:C1,m1,C2,m2皆为待定常数,ReB为宾汉雷诺数,fs为壳侧阻力系数。
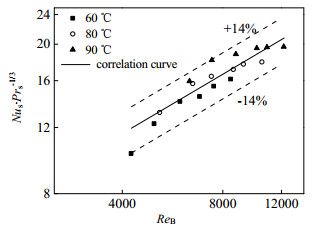
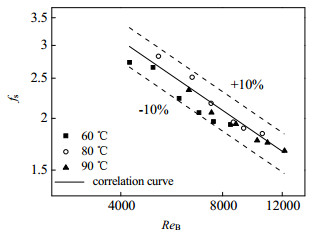
根据实验数据,拟合了壳侧水煤浆传热和阻力系数实验关联式,如图 13和图 14和式(29)和式(30)所示,可以看到实验数据与Nus拟合关联式之间的偏差不超过14.05%,与fs拟合关联式之间的偏差不超过10.33%,关联式与实验数据符合较好。
| $ N{u_{\rm{s}}} = 0.149Re_{\rm{B}}^{0.524}Pr_{\rm{s}}^{1/3} $ | (29) |
| $ {f_{\rm{s}}} = 239.332Re_{\rm{B}}^{ - 0.530} $ | (30) |
|
图 13 Nus·Prs-1/3随ReB的变化 Fig.13 Relationship between Nus·Prs-1/3 and ReB |
|
图 14 fs随ReB的变化 Fig.14 Relationship between fs and ReB |
从以上数据可以看出,提高水煤浆预热换热器中热流体的定性温度或者增大水煤浆的流量都可以增强水煤浆预热换热器的换热能力。在条件允许的范围内应尽量提高热流体的温度,这样不仅增大热流体和水煤浆之间的温差,让换热器的换热量得以提高,也使水煤浆的定性温度提高,黏度降低,减小了水煤浆在换热器内的压降,同时水煤浆黏度和导热油黏度的降低还让冷热流体之间换热增强,使总传热系数增大。在之后的研究和工业生产中,还可以采用高温蒸汽作为热流体预热水煤浆,利用蒸汽与待预热水煤浆之间巨大的温差和蒸汽侧极高的传热膜系数,使水煤浆预热换热器获得更好的预热能力。
结合本文数据,在预热水煤浆时选择较小的流量可以使水煤浆以较小的压降流过换热器,让单位压降温升和单位压降总传热系数保持在较高水平,减少了由压降带来的运行费用。但是较小的流量会让换热器的总传热系数相对较小,换热器一部分的换热能力没有得到充分发挥,这又要求采用更大或者更多的换热器来满足预热要求,增加了设备成本。如果在预热水煤浆时选择较大的流量可以使换热器的总传热系数相对较大,使换热器的换热能力得到充分发挥,降低了设备成本,但同时较大的流量带来了较大的压降,单位压降温升和单位压降总传热系数有所降低,这又增加了由压降带来的运行费用。
工业生产中,煤气化企业可能面临两种典型情况,其一是为保证入炉压力[38-39],必须限制水煤浆在预热时的压降,或者企业主要考虑长期的运行费用。此时应尽量选较小的流量以获得较大的单位压降温升和单位压降总传热系数。但需注意流量不能过小而导致水煤浆在换热器内的沉积和堵塞。其二是对压降的要求不高,或者比较重视设备的制造或更换费用。这时应选较大的水煤浆流量让换热器的总传热系数达到较高的水平,但需要注意总传热系数的增大速率会随流量增大而降低,应该选取比较经济的流量。本文3.4节得到的水煤浆预热换热器壳侧实验关联式也可以为工况选择提供参考。
4 结论本文实验研究了在旋梯折流板换热器的壳侧预热水煤浆的可行性,比较了不同导热油定性温度下水煤浆温升、压降、单位压降温升、总传热系数以及单位压降总传热系数,得到了壳侧传热和阻力系数关联式,同时对选取水煤浆预热换热器的工况进行了讨论。主要结论如下:
(1) 实验证明,在旋梯折流板换热器的壳侧预热水煤浆是可行的,且水煤浆在换热器内的流动传热性能良好。水煤浆在换热器壳侧流动可以提高湍流程度和传热膜系数,避免水煤浆堵塞换热管,有利于在后期研究和应用中采用各种壳侧传热强化措施增强预热效果。本文的研究还为进一步开展更高质量分数水煤浆的预热研究打下了基础。
(2) 水煤浆温升、总传热系数随导热油定性温度的增加而增大,同时压降随导热油定性温度的增加而降低,当导热油的定性温度约为80和90 ℃时,相比导热油的定性温度约为60 ℃,单位压降温升分别提高了80.92%~87.16%和148.92%~189.00%,单位压降总传热系数分别提高了59.88%~63.31%和111.09%~144.63%。这说明在条件允许的情况下,应尽量提高预热水煤浆的热流体的定性温度。
(3) 在预热水煤浆时选择较小的流量可以降低压降,提高单位压降温升和单位压降总传热系数,但是总传热系数不高,换热器的换热能力没有得到充分发挥;选择较大的流量可以提高总传热系数,但是单位压降温升和单位压降总传热系数相应降低,在选择预热水煤浆的工况时应该结合具体情况进行分析。本文得到的水煤浆预热换热器壳侧实验关联式也可以为工况选择提供参考。
符号说明:
|
|
| [1] |
MUSA S D, TANG Z, IBRAHIM A O, et al. China's energy status: A critical look at fossils and renewable options[J]. Renewable & Sustainable Energy Reviews, 2017, 81(2): 2281-2290. |
| [2] |
ZHANG X, WINCHESTER N, ZHANG X. The future of coal in China[J]. Energy Policy, 2017, 110(11): 644-652. |
| [3] |
PENG B H, GUO D N, QIAO H, et al. Bibliometric and visualized analysis of China's coal research 2000-2015[J]. Journal of Cleaner Production, 2018, 197(1): 1177-1189. |
| [4] |
CHANG S, ZHUO J, MENG S, et al. Clean coal technologies in China: current status and future perspectives[J]. Engineering, 2016, 2(4): 447-459. DOI:10.1016/J.ENG.2016.04.015 |
| [5] |
CHEN W, XU R. Clean coal technology development in China[J]. Energy Policy, 2010, 38(5): 2123-2130. DOI:10.1016/j.enpol.2009.06.003 |
| [6] |
孙漾, 顾幸生. 水煤浆气化装置操作优化技术及其应用[J]. 化工学报, 2012, 63(9): 2799-2804. SUN Y, GU X S. Coal water slurry gasification unit operation optimization technology and its application[J]. CIESC Journal, 2012, 63(9): 2799-2804. DOI:10.3969/j.issn.0438-1157.2012.09.020 |
| [7] |
黄桃花, 王亦飞, 焦延涛, 等. 高效能两段组合式煤气化过程热态试验[J]. 化工学报, 2010, 61(11): 2924-2930. HUANG T H, WANG Y F, JIAO Y T, et al. Hot-state experiment of high-performance two stage combined coal gasification[J]. CIESC Journal, 2010, 61(11): 2924-2930. |
| [8] |
夏德宏, 唐献红, 王世均. 水煤浆预热对燃烧的影响[J]. 冶金能源, 1992, 11(5): 30-31. XIA D H, TANG X H, WANG S J. Influence of preheating on CWS combustion[J]. Energy for Metallurgical Industry, 1992, 11(5): 30-31. |
| [9] |
KATAYAMA Y, TAMAURA Y. Development of new green-fuel production technology by combination of fossil fuel and renewable energy[J]. Energy, 2005, 30(11): 2179-2185. |
| [10] |
NOVACK M, ROFFE G, MILLER G. Combustion of coal/water mixtures with thermal preconditioning[J]. Journal of Engineering for Gas Turbines and Power, 1987, 109(3): 313-318. DOI:10.1115/1.3240041 |
| [11] |
AIUCHI K, MORIYAMA R, TAKEDA S, et al. A pre-heating vaporization technology of coal-water-slurry for the gasification process[J]. Fuel Processing Technology, 2007, 88(4): 325-331. DOI:10.1016/j.fuproc.2004.10.010 |
| [12] |
WANG Q, ZENG M, MA T, et al. Recent development and application of several high-efficiency surface heat exchangers for energy conversion and utilization[J]. Applied Energy, 2014, 135(12): 748-777. |
| [13] |
王斯民, 肖娟, 王家瑞, 等. 基于流固耦合理论的螺旋折流板换热器结构优化研究[J]. 高校化学工程学报, 2017, 31(3): 539-546. WANG S M, XIAO J, WANG J R, et al. Structural optimization of shell-tube heat exchanger with helical baffles based on fluid-structure interaction[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(3): 539-546. DOI:10.3969/j.issn.1003-9015.2017.00.018 |
| [14] |
WEN J, YANG H Z, WANG S M, et al. Experimental investigation on performance comparison for shell-and-tube heat exchangers with different baffles[J]. International Journal of Heat & Mass Transfer, 2015, 84(5): 990-997. |
| [15] |
SALAHUDDIN U, BILAL M, EJAZ H. A review of the advancements made in helical baffles used in shell and tube heat exchangers[J]. International Communications in Heat & Mass Transfer, 2015, 67(10): 104-108. |
| [16] |
文键, 杨辉著, 王斯民, 等. 旋梯式螺旋折流板换热器优化结构的数值模拟[J]. 西安交通大学学报, 2014, 48(11): 8-14. WEN J, YANG H Z, WANG S M, et al. Numerical simulation for configuration optimization of heat exchanger with helical baffles[J]. Journal of Xi'an Jiaotong University, 2014, 48(11): 8-14. |
| [17] |
文键, 杨辉著, 薛玉兰, 等. 旋梯式螺旋折流板换热器换热性能的实验研究[J]. 高校化学工程学报, 2015, 29(4): 795-801. WEN J, YANG H Z, XUE Y L, et al. Experimental investigation on heat transfer performance of heat exchanger with ladder-type fold baffles[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(4): 795-801. DOI:10.3969/j.issn.1003-9015.2015.04.004 |
| [18] |
孟令杰, 孔珑, 章名耀. 水煤浆管内流动的相似准数及其阻力特性[J]. 化工学报, 1995, 46(3): 298-303. MENG L J, KONG L, ZHANG M Y. Similitude criterion and resistence characteristics of coal-water-slurry flowing in pipe[J]. Journal of Chemical Industry and Engineering (China), 1995, 46(3): 298-303. |
| [19] |
CHEN L Y, DUAN Y F, PU W H, et al. CFD simulation of coal-water slurry flowing in horizontal pipelines[J]. Korean Journal of Chemical Engineering, 2009, 26(4): 1144-1154. |
| [20] |
陈良勇, 段钰锋, 刘猛, 等. 水平管入口段内水煤浆流动特性数值模拟[J]. 东南大学学报, 2010, 40(2): 402-408. CHEN L Y, DUAN Y F, LIU M, et al. Numerical study of developing coal-water slurry flow in entrance region of horizontal pipe[J]. Journal of Southeast University, 2010, 40(2): 402-408. DOI:10.3969/j.issn.1001-0505.2010.02.036 |
| [21] |
任远, 陈良勇, 赵国华, 等. 水煤浆流经渐缩管段的局部阻力特性[J]. 动力工程学报, 2008, 28(4): 651-656. REN Y, CHEN L Y, ZHAO G H, et al. Study on local energy losses of coal water slurry flowing in gradual shrinking tubes[J]. Chinese Journal of Power Engineering, 2008, 28(4): 651-656. DOI:10.3321/j.issn:1000-6761.2008.04.032 |
| [22] |
史美中, 王中铮. 热交换器原理与设计[M]. 南京: 东南大学出版社, 2014. SHI M Z, WANG Z Z. Principle and design of heat exchangers[M]. Nanjing: Southeast University Press, 2014. |
| [23] |
钱颂文. 换热器设计手册[M]. 北京: 化学工业出版社, 2002. QIAN S W. Heat exchanger design manual[M]. Beijing: Chemical Industry Press, 2002. |
| [24] |
MARADIYA C, VADHER J, AGARWAL R. The Heat transfer enhancement techniques and their thermal performance factor[J]. Beni-Suef University Journal of Basic and Applied Sciences, 2017, 7(1): 1-21. |
| [25] |
林文珠, 曹嘉豪, 方晓明, 等. 管壳式换热器强化传热研究进展[J]. 化工进展, 2018, 37(4): 1276-1286. LIN W Z, CAO J H, FANG X M, et al. Research progress of heat transfer enhancement of shell-and-tube heat exchanger[J]. Chemical Industry and Engineering Progress, 2018, 37(4): 1276-1286. |
| [26] |
王振华, 邢芳. 流体在换热器管程侧或壳程侧的选择[J]. 广州化工, 2018, 46(7): 108-110. WANG Z H, XING F. Allocation of stream in shell side or tube side[J]. Guangzhou Chemical Industry, 2018, 46(7): 108-110. DOI:10.3969/j.issn.1001-9677.2018.07.036 |
| [27] |
WEN J, GU X, WANG M, et al. Numerical investigation on the multi-objective optimization of a shell-and-tube heat exchanger with helical baffles[J]. International Communications in Heat and Mass Transfer, 2017, 89(12): 91-97. |
| [28] |
YOU Y, FAN A, HUANG S, et al. Numerical modeling and experimental validation of heat transfer and flow resistance on the shell side of a shell-and-tube heat exchanger with flower baffles[J]. International Journal of Heat & Mass Transfer, 2012, 55(25-26): 7561-7569. |
| [29] |
WANG X, ZHENG N, LIU P, et al. Numerical investigation of shell side performance of a double shell side rod baffle heat exchanger[J]. International Journal of Heat & Mass Transfer, 2017, 108(3): 2029-2039. |
| [30] |
杨世铭, 陶文铨. 传热学[M]. 第4版. 北京: 高等教育出版社, 2006. YANG S M, TAO W Q. Heat transfer[M]. 4th ed. Beijing: Higher Education Press, 2006. |
| [31] |
谢东.水煤浆流变特性及其检测技术研究[D].武汉: 华中科技大学, 2010. XIE D. Research on rheological characteristics of coal water slurry and its measurement technologies[D]. Wuhan: Huazhong University of Science and Technology, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10487-1011035943.htm |
| [32] |
MOFFAT R J. Describing the uncertainties in experimental results[J]. Experimental Thermal & Fluid Science, 1988, 1(1): 3-17. |
| [33] |
AKBARI A, KOURAVAND S, CHEGINI G. Experimental analysis of a rotary heat exchanger for waste heat recovery from the exhaust gas of dryer[J]. Applied Thermal Engineering, 2018, 138(6): 668-674. |
| [34] |
ROH N S, SHIN D H, KIM D C, et al. Rheological behaviour of coal-water mixtures. 2. Effect of surfactants and temperature[J]. Fuel, 1995, 74(9): 1313-1318. DOI:10.1016/0016-2361(95)00085-J |
| [35] |
CHURCHILL S W, BERNSTEIN M A. A correlating equation for forced convection from gases and liquids to circular cylinder in cross flow[J]. Journal of Heat Transfer, 1977, 99(2): 300-306. DOI:10.1115/1.3450685 |
| [36] |
CENGEL Y A. Heat transfer: approach[M]. New York: McGraw-Hill, 2007.
|
| [37] |
ZHANG J F, LI B, HUANG W J, et al. Experimental performance comparison of shell-side heat transfer for shell-and-tube heat exchangers with middle-overlapped helical baffles and segmental baffles[J]. Chemical Engineering Science, 2009, 64(8): 1643-1653. DOI:10.1016/j.ces.2008.12.018 |
| [38] |
ZHENG L, FURINSKY E. Comparison of shell, texaco, BGL and KRW gasifiers as part of IGCC plant computer simulations[J]. Energy Conversion & Management, 2005, 46(11): 1767-1779. |
| [39] |
刘文, 尹晓晖, 李克海. 水煤浆气化制氢的气化压力选择[J]. 洁净煤技术, 2016, 22(5): 89-94. LIU W, YIN X H, LI K H. Pressure selection of coal to hydrogen by coal water slurry gasification technology[J]. Clean Coal Technology, 2016, 22(5): 89-94. |




