2. 教育部超重力工程技术中心 北京化工大学,北京 100029
2. Research Center of the Ministry of Education for High Gravity Engineering and Technology, Beijing University of Chemical Technology, Beijing 100029, China
旋转填充床(RPB)在强化传质和微观混合等方面有着独特的优势[1]。相比于传统化工设备,旋转填充床利用超重力技术能够提高产品质量,降低能耗,且设备体积较小[2],广泛应用于纳米材料、药物制备、油田注水脱氧等领域[3]。填料作为旋转床核心内构件之一,其结构对混合/传质效率有着显著影响[4-5],因此研究填料内流体流动特征尤为重要。
孙润林等[6]利用高速摄像技术,拍摄到不同丝径填料空腔区内液滴,获得液滴的平均直径和速度。Yang等[7]采用X-ray CT技术,捕获到各种操作条件下丝网和泡沫镍填料内液体分布图,对持液量进行了定量描述。Gao等[8]采用PIV技术对气体流动特性进行测量,通过对气相流场的分析为气固相催化反应的进一步研究提供了理论依据。然而,由于复杂的填料结构及实验的偶然性等因素,通过实验方法对流体流动状况进行观测较为复杂。
近年来,随着计算流体力学与计算机的发展,CFD方法逐步成为分析流体流动特征及传质过程的有效工具[9-10]。吴祖钰等[11]基于简化的旋转床几何结构建立了二维CFD模型,结果表明相比于三角形螺旋填料,正三角形填料气相压降的模拟值与实验值更为吻合。Yang等[12]建立了旋转床的三维CFD模型,在进口处加设挡板优化气体分布,并发现孔隙率是影响RPB内流场的重要因素之一。然而将填料简化为多孔介质模型的方法,由于其物理模型与实际存在较大差距,无法真实地阐明填料区流体流动特征。Liu等[13]构建出较为真实的丝网填料,通过CFD模拟获得填料内气相流动状况,揭示气相端效应区的存在,但其模型网格数高达九千万以上,导致计算量大且收敛精度低。
本文建立了球填料旋转床的三维CFD模型,对气相流动行为进行模拟研究,采用实验结果进行验证;进而分析旋转床内气相流场特性,研究转速与气量对气速、总压、湍动能及平均停留时间的影响规律。
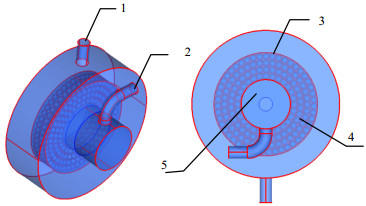
2 模型的建立及计算方法 2.1 物理模型基于实验的球填料旋转床结构,采用CAD软件建立了图 1所示三维几何模型,主要由进口管、出口管、内空腔、填料区和外空腔组成,球填料分三层均匀排布在转子区,旋转床及球填料尺寸如表 1所示。
|
图 1 球填料旋转床的三维物理模型 Fig.1 Three dimensional model of the rotating ball packed bed 1. gas inlet 2. gas outlet 3. outer cavity 4. packing 5. inner cavity |
|
|
表 1 旋转填充床结构尺寸 Table 1 Structural size of the rotating packed bed |
使用Ansys ICEM14.5软件对旋转填充床物理模型划分网格。采用非结构网格,填料区球填料排布较为复杂,故对填料区加密处理,以提高网格质量减小误差。对规整球填料模型进行网格无关性验证,得到最优网格为944万网格。
2.3 计算模型及方法本文模拟旋转填充床内的气相流动,气相在离心力作用下做强旋运动,无传质、传热过程,故只需求解动量与质量守恒方程。
当气体流动稳定时,各参数不随时间变化,故采用稳态模型进行模拟求解。稳态模型中各参数不随时间变化,故连续性方程为:
| $ \frac{{\partial (\rho {u_x})}}{{\partial x}} + \frac{{\partial (\rho {u_y})}}{{\partial y}} + \frac{{\partial (\rho {u_z})}}{{\partial z}} = {S_{\rm{m}}} $ | (1) |
对动量方程,则分为静止区与旋转区两个部分。对于静止区有以下方程:
| $ \frac{\partial \rho {{u}_{i}}{{u}_{j}}}{\partial {{x}_{j}}}=-\frac{\partial p}{\partial {{x}_{i}}}+\mu \frac{{{\partial }^{2}}{{u}_{i}}}{\partial {{x}_{j}}\partial {{x}_{j}}}+\text{ }\frac{\partial \left( -\rho \overline{u_{i}^{'}u_{j}^{'}} \right)}{\partial {{x}_{j}}}\text{+}\rho {{S}_{\text{F}}} $ | (2) |
式中,P为静压力,SF是动量守恒方程源项。在旋转区则采用MRT方程,将速度参数u进行修改:
| $ {u_{\rm{r}}} = u - {v_{\rm{r}}} $ | (3) |
| $ {v_{\rm{r}}} = {v_{\rm{t}}} + \omega \times r $ | (4) |
式中,vt为移动区域的平移速度,ω为角速度。从而得到:
| $ \frac{\partial (\rho {{{\vec{u}}}_{\text{r}}})}{\partial t}+\nabla \cdot (\rho {{\vec{u}}_{\text{r}}}{{\vec{u}}_{\text{r}}})+\rho (\text{2}\vec{\omega }\times {{\vec{u}}_{\text{r}}}+\vec{\omega }\times \vec{\omega }\times \vec{r}+\vec{\alpha }\times \vec{r}+\vec{a})=-\nabla p+\nabla {{\bar{\bar{\bar{\tau }}}}_{\text{r}}}+\vec{F} $ | (5) |
分别采用Standard k-ε湍流模型与Realizable k-ε湍流模型进行方程封闭。
(1) Standard k-ε模型[14]
湍动能方程:
| $ \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {(\mu + \frac{{{u_{\rm{t}}}}}{{{\sigma _{\rm{k}}}}})\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_{\rm{k}}} + {G_{\rm{b}}} - \rho \varepsilon - {Y_{\rm{M}}} + {S_{\rm{k}}} $ | (6) |
湍流耗散速率方程:
| $ \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {(\mu + \frac{{{u_{\rm{t}}}}}{{{\sigma _{\rm{ \mathsf{ ε} }}}}})\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + {C_{{\rm{1 \mathsf{ ε} }}}}\frac{\varepsilon }{k}({G_{\rm{k}}} + {C_{3{\rm{ \mathsf{ ε} }}}}{G_b}) - {C_{{\rm{2 \mathsf{ ε} }}}}\rho \frac{{{\varepsilon ^2}}}{k} + {S_{\rm{ \mathsf{ ε} }}} $ | (7) |
式中,ρ为流体密度,k为湍动能,u为流速,μ为流体动力黏度,Gk为平均速度梯度产生的湍动能,Gb为浮力产生的湍动能,YM表示可压缩湍流中脉动扩展对耗散率的影响,C1ε = 1.44、C2ε = 1.9为经验常数,σk = 1.0、σε = 1.2为k和ε方程的湍流普朗特常数,Sk和Sε为湍动能和湍流耗散率源项。
(2) Realizable k-ε模型[15]
湍动能方程:
| $ \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {(\mu + \frac{{{u_{\rm{t}}}}}{{{\sigma _{\rm{k}}}}})\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_{\rm{k}}} + {G_{\rm{b}}} - \rho \varepsilon - {Y_{\rm{M}}} + {S_{\rm{k}}} $ | (8) |
湍流耗散速率方程:
| $ \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {(\mu + \frac{{{u_{\rm{t}}}}}{{{\sigma _{\rm{ \mathsf{ ε} }}}}})\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + {C_{{\rm{1 \mathsf{ ε} }}}}\frac{\varepsilon }{k}{C_{{\rm{3 \mathsf{ ε} }}}}{G_b} - {C_{2{\rm{ \mathsf{ ε} }}}}\rho \frac{{{\varepsilon ^2}}}{{k + \sqrt {\varepsilon \upsilon } }} + \rho {C_{\rm{1}}}E\varepsilon $ | (9) |
本文利用上述计算模型,采用规整球填料模型与多孔介质模型,模拟气相流动,并计算压降值。规整球填料模型中,在填料区构建三层均匀的填料球,与真实球填料堆积排布方式相近。在流体流动中,填料球对流体产生阻碍等作用,模拟流场流动状态。多孔介质模型简化了填料内部结构[12],在填料区添加作用力,即在动量方程中添加源项,源项包含黏性阻力与惯性阻力,使其更接近真实填料。
2.4 边界条件及求解方法进口边界条件设置为质量流率进口,湍流强度采用公式
计算采用FLUENT14.5商用软件,采用SIMPLE算法进行压力与速度耦合,二级迎风方法计算动量、湍动能和耗散率。当参数残差值达到10-3,并且所监测进口、出口压力稳定后视为收敛。
3 结果和讨论 3.1 模型验证首先对旋转床内气相流动行为进行数值模拟,以氮气为介质计算床层压降,然后通过实验数据进行模型验证。实验采用卧式旋转床,气体由径向进口进入,流经外空腔由转子外缘逐渐向中心汇集,最后经由内空腔从出口管排出;用压差计测量旋转床进出口压降,记录干床压降。
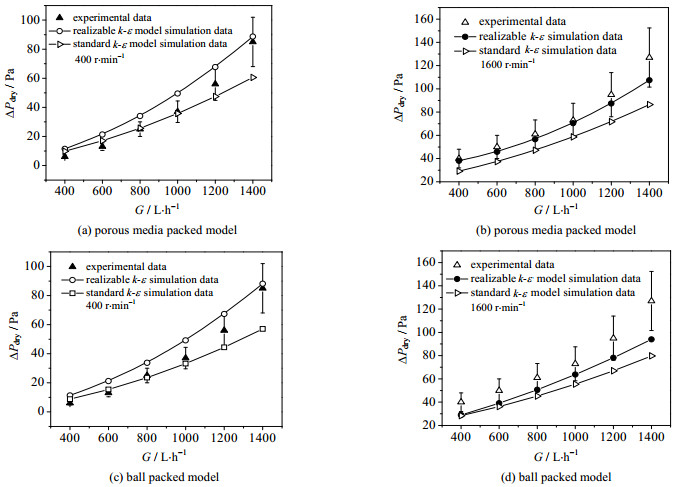
图 2分别为转速400和1600 r·min-1下,多孔介质模型与球填料模型中压降随气量的变化曲线。由图 2可知,采用Standard k-ε模型模拟,在低转速低气量下模拟值误差在±20%以内,但随着转速与气量的增加,模拟值逐渐超出误差线,主要由于旋转填充床内通常伴有旋涡等流动。Realizable k-ε模型对湍流黏度和耗散率等模型参数进行了修正,考虑了不同类型的流动[15]。采用该模型时在低气量低转速下误差较大,随着转速与气量的增加误差值下降,相对于Standard k-ε拟合趋势较好。对比多孔介质模型与球填料模型,两者模拟结果较为接近,表明多孔介质模型与球填料模型皆可用于气相压降的计算。
|
图 2 气量对压降的影响 Fig.2 Effects of gas flow rate on dry pressure drop |
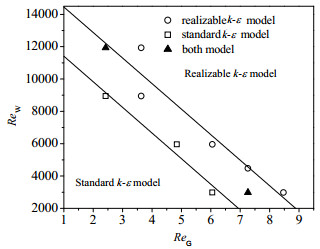
引入两个无量纲雷诺数分析不同条件下湍流模型的适用性,其中
|
图 3 湍流模型与ReG、Reω的关系 Fig.3 Relationship between turbulent model and ReG, Reω |
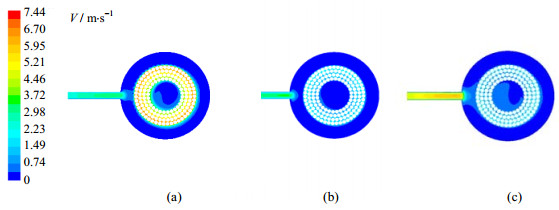
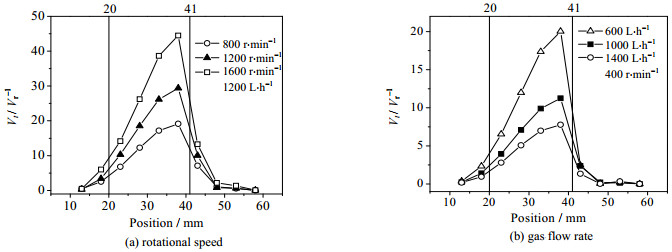
图 4为不同操作条件下RPB径向截面的速度分布云图。对比(a)(b)可知,转速增大时填料区的气速明显升高,内外空腔气速变化较小。对比(b)(c)可知,气量会影响进口与出口区域的速度,对填料层速度影响较小。本文将对切向速度与径向速度进行分析,将旋转床划分为不同的圆环体,计算切向速度与径向速度的比值(Vt·Vr-1),如图 5所示。由图 5可见,填料区气体速度由切向速度主导,内外空腔气体速度由径向速度主导,在填料区两速度比值沿径向呈逐渐增大趋势,而内外空腔比值较小;转速增加时切向速度增大,比值增大;气量增大使得径向速度增大,比值降低。
|
图 4 RPB内速度分布云图 Fig.4 Contours of velocity in RPB (a) 1600 r·min-1, 600 L·h-1 (b) 400 r·min-1, 600 L·h-1 (c) 400 r·min-1, 1200 L·h-1 |
|
图 5 切向速度与径向速度比值的径向分布 Fig.5 Radial distribution of the ratio of tangential to radial velocity |
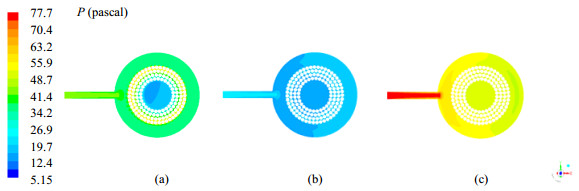
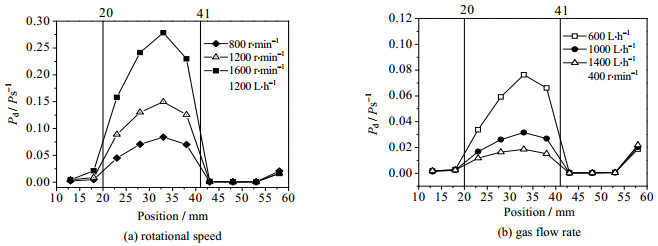
图 6为不同操作条件下球填料旋转床内总压分布云图。气体从进口管流入外空腔,由于流道突然扩大,气速降低,摩擦阻力减小,总压降低;气体进入填料区后,获得离心力,总压上升,随后在摩擦阻力的作用下,总压沿径向降低。由图 6可知,高转速会使总压升高,压降增大,其原因为气体压降与离心力成正比,高转速使离心力增强[1]。气量增大时会增大气相摩擦力,故压降增大。RPB内动压与静压比(Pd·Ps-1)的径向分布如图 7所示。由图 7可知,在内外空腔区,由于气速较小,动压数值低,此时动静压比值很小;由于填料区气速较高,动静压比值较大,提高转速其比值增大,增加气量其比值下降。
|
图 6 RPB总压分布云图 Fig.6 Contours of total pressure in RPB (a) 1600 r·min-1, 600 L·h-1 (b) 400 r·min-1, 600 L·h-1 (c) 400 r·min-1, 1200 L·h-1 |
|
图 7 动压与静压比值沿径向分布 Fig.7 Radial distribution of the ratio of dynamic to static pressure |
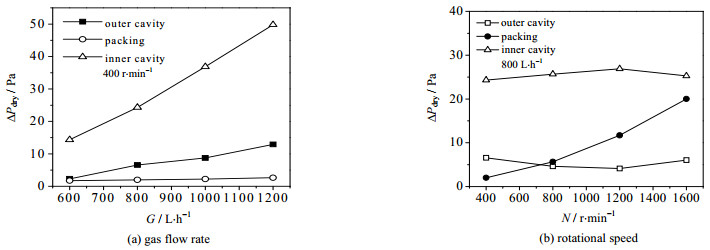
图 8表示转速和气量对外空腔、填料区及内空腔三个区域压降的影响规律。从图可以看出,气量增加,内外空腔区域压降都呈现增大趋势,填料区压降变化不明显。由于高气量使内外空腔气速增大,摩擦阻力损失上升,故压降增大。转速升高,填料区压降增大,内外空腔压降变化较小。因为填料区内气速与填料转速成正相关,转速越高则气速越大,压降增加。
|
图 8 旋转床内各区域的压降 Fig.8 Pressure drop in different zones of RPB |
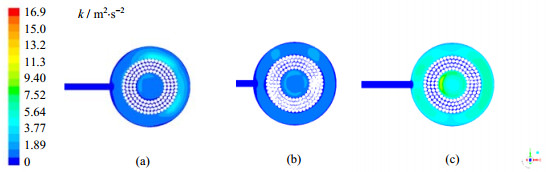
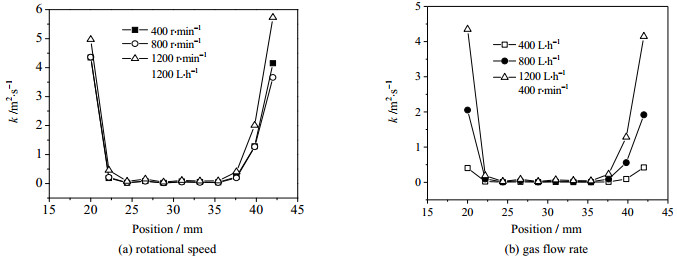
图 9为RPB径向截面的湍动能分布云图,图 10为湍动能沿径向分布。由图 9、图 10可知,由于填料区填料排布密集,气体几乎与填料同步运动[8],因而湍动能较低,且随操作条件变化幅度较小。由于转速主要作用于填料区,故转速增大时,湍动能有较小幅度增大。当气量增大时,气体的径向速度与切向速度的作用增大,同时气体更为剧烈的撞击填料,因而湍动能增强。
|
图 9 RPB湍动能分布图 Fig.9 Contours of turbulent kinetic energy in RPB (a) 1600 r·min-1, 600 L·h-1 (b) 400 r·min-1, 600 L·h-1 (c) 400 r·min-1, 1200 L·h-1 |
|
图 10 湍动能沿径向分布 Fig.10 Radial distribution of turbulent kinetic energy |
前人对旋转床内液相停留时间已有研究,而气相停留时间至今未见公开文献报道。实验测量气体停留时间难度较大,故本文利用CFD技术,应用脉冲法计算气相在旋转床内的平均停留时间。首先建立稳态的气相流场,待其稳定收敛后,将一个时间步长(0.0005 s)的示踪剂在入口处注入并进行非稳态计算。平均停留时间为
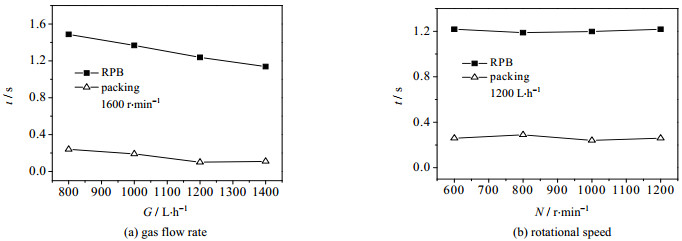
图 11表示气量和转速对平均停留时间的影响规律。由图 11可知,气量增大时RPB与填料区的气相平均停留时间减小,其原因为气量增高会导致径向速度增大,故平均停留时间降低;气相平均停留时间随转速提高略有波动,但幅度不大,由于转速主要对切向速度有影响,对径向速度影响不大,故转速对平均停留时间影响较小。
|
图 11 操作参数对平均停留时间的影响 Fig.11 Effects of operational parameters on mean residence times |
构建了球填料旋转床内气相流动的三维CFD模型,模拟了RPB内的气相流动特征,主要结论如下:
(1) 分别采用Standard k-ε和Realizable k-ε两种湍流模型进行方程封闭,通过实验验证,确定两种湍动模型适用的操作范围;同时结果也表明建立球填料模型和多孔介质模型模拟气相压降可行。
(2) 对球填料模型中气相流动进行数值模拟,结果表明:切向速度、填料区压降、湍动能随转速增大而增大,内外空腔压降受转速影响较小;径向速度、内外空腔压降、湍动能随气量增大而增大,填料区压降受气量影响较小。
(3) 探究气量和转速对旋转床内气相平均停留时间的影响,结果表明:气量增大时平均停留时间减小,转速的变化对其影响较小。
符号说明:
| C1ε, C2ε, C3ε | —经验常数 | Sk Sε | —湍动能和湍流耗散率源项 |
| di | —入口直径,m | SF | —动量守恒方程的源项 |
| DH | —水力直径,m | u | —气速,m·s-1 |
| Gb | —浮力产生的湍动能,m2·s-2 | U0 | —入口气速,m·s-1 |
| Gk | —平均速度梯度产生的湍动能,m2·s-2 | vt | —移动区域的平移速度,m·s-1 |
| I | —湍流强度 | YM | —可压缩湍流中脉动扩展对耗散率的影响 |
| k | —湍动能,m2·s-2 | σk、σε | —湍流普朗特常数常数 |
| R | —填料当量直径,m | ω | —角速度,rad·s-1 |
| ReG | —气相雷诺数 | μ | —黏度kg·(m·S)-1 |
| Reω | —旋转雷诺数 | ρ | —密度kg·m-3 |
| Re | —雷诺数 |
| [1] | Rao D P, Bhowal A, Goswami P S. Process intensification in rotating packed beds (HIGEE):an appraisal[J]. Industrial and Engineering Chemistry Research, 2004, 43(4): 1150-1162. DOI:10.1021/ie030630k. |
| [2] | ZOU Hai-kui(邹海魁), CHU Guang-wen(初广文), XIANG Yang(向阳), et al. New progress of HIGEE reaction technology(超重力反应强化技术最新进展)[J]. Journal of Chemical Industry and Engineering(化工学报), 2015, 66(8): 2806-2809. |
| [3] | ZOU Hai-kui(邹海魁), SHAO Lei(邵磊), CHEN Jian-feng(陈建峰). Progress of higee technology-from laboratory to commercialization(超重力技术进展-从实验室到工业化)[J]. CIESC Journal(化工学报), 2015, 66(8): 2806-2809. |
| [4] | JIAO Wei-zhou(焦纬洲), LIU You-zhi(刘有智), QI Gui-sheng(祁贵生). Research progress in the structures of packings for high-gravity rotating packed bed(超重力旋转床填料结构研究进展)[J]. Natural Gas Chemical Journal(天然气化工), 2008, 33(6): 67-72. DOI:10.3969/j.issn.1001-9219.2008.06.015. |
| [5] | JIAN Qi-fei(简弃非), DENG Xian-he(邓先和), ZHANG Ya-jun(张亚君), et al. Influence of packing plate distance of high-gravity rotating bed on gas phase resistance(超重力旋转床片状填料间距对气相阻力的影响)[J]. Journal of Chemical Industry and Engineering(化工学报), 2000, 51(3): 429-433. DOI:10.3321/j.issn:0438-1157.2000.03.028. |
| [6] | SUN Run-lin(孙润林), XIANG Yang(向阳), YANG Yu-cheng(杨宇成), et al. A visual study of liquid flow in a rotating packing bed with super gravity(超重力旋转床液体流动的可视化研究)[J]. Journal of Chemical Engineering of Chinese Universities(化工学报), 2013, 27(3): 412-416. |
| [7] | Yang Y C, Xiang Y, Chu G W, et al. A noninvasive X-ray technique for determination of liquid holdup in a rotating packed bed[J]. Chemical Engineering Science, 2015, 138(12): 244-255. |
| [8] | Gao X Y, Chu G W, Ouyang Y, et al. Gas flow characteristics in a rotating packed bed by particle image velocimetry measurement[J]. Industrial and Engineering Chemistry Research, 2017, 56(11): 14350-14361. |
| [9] | Visser D C, Houkema M, Siccama N B, et al. Validation of a FLUENT CFD model for hydrogen distribution in a containment[J]. Nuclear Engineering and Design, 2012, 245(3): 161-171. |
| [10] | Liu H S, Lin C C, Wu S C, et al. Characteristics of a rotating packed bed[J]. Industrial and Engineering Chemistry Research, 1996, 35(10): 3590-3596. DOI:10.1021/ie960183r. |
| [11] | WU Zu-yu(吴祖钰), RUAN Qi(阮奇), FAN Shu-jie(凡书杰), et al. Numerical simulation on pressure drop of rotating packed bed with triangular spiral packing(三角形螺旋填料旋转床气相压降的数值模拟)[J]. Computers and Applied Chemistry(计算机与应用化学), 2011, 28(6): 704-708. DOI:10.3969/j.issn.1001-4160.2011.06.011. |
| [12] | Yang Y C, Xiang Y, Li Y G, et al. 3D CFD nodelling and optimization of single-phase flow in rotating packed beds[J]. Canadian Journal of Chemical Engineering, 2015, 93(6): 1138-1148. DOI:10.1002/cjce.v93.6. |
| [13] | Liu Y, Luo Y, Chu G W, et al. 3D numerical simulation of a rotating packed bed with structured stainless steel wire mesh packing[J]. Chemical Engineering Science, 2017, 170(1): 365-377. |
| [14] | Launder B E, Spalding D B. Lectures in mathematical models of turbulence[M].London: Academic Press, 1972. |
| [15] | Shih T H, Liou W W, Shabbir A, et al. A new k-ε eddy-viscosity model for high reynolds number turbulent flows-model development and validation[J]. Computers Fluids, 1995, 24(3): 227-238. DOI:10.1016/0045-7930(94)00032-T. |




