2. 浙江大学 能源清洁利用国家重点实验室,浙江 杭州 310027
2. State Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou 310027, China
超临界流体是温度高于临界温度Tc与压力高于其临界压力pc的特殊流体,由于其普遍具有较高的氧化性、溶解度和扩散系数,因此常被用做氧化剂[1-2]或催化剂[3]等反应介质。近年来,随着对超临界流体物性研究的不断深入,其密度的局部不均匀性受到了研究人员的广泛关注,并采用分子动力学方法进行了研究。分子动力学方法可从微观机理角度解释宏观现象并且不受实验技术限制,可模拟极端条件下的体系并计算得到相关物理量[4],是研究以超临界水(临界温度与压力分别为647.15 K与22.1 MPa)为代表的超临界流体物性的有力工具。
SKARMOUTSOS等[5]发现温度为666 K的超临界水(模拟的水分子数量为500个,密度范围为0.2 ρc~2 ρc,ρc为水的临界密度)存在局部密度与结构的不均匀性,而且含氢键流体的局部密度不均匀性更大[5-6]。氢键的键能介于共价键和范德华力之间,考虑分子间氢键的平均强度,形成一个氢键则增强了其周围氢键的协同作用,且氢键的协同作用可使水分子以大的团簇结构存在[7]。MA等[8]从氢键数量与体系能量波动来解释这种不均匀性,并发现温度在666 K的条件下,密度在低于0.19 ρc时能量波动急剧增加,此时四面体序参数有最小值,体系短程有序被破坏。SKARMOUTSOS等[9]发现当温度为666 K时,周围有1个和2个氢键的水分子对超临界水的局部密度不均匀性的贡献最大,并从三角形和四面体序参数角度揭示了局部有序性与氢键的关系。SAHLE等[10]则通过从头分子动力学模拟和密度泛函理论方法,发现在温度低于873 K与压力低于132 MPa的超临界水中仍然存在着氢键网络。
由于密度不均匀性可能引起超临界水中氢键特性的变化,并且氢键作为贡献较大的分子间相互作用,其数量、键能大小及空间分布会对超临界水的物性造成重要影响。因此对氢键特性及其空间分布随密度变化的研究尤为重要。但是目前文献中关于超临界水密度对氢键键能及其空间分布影响的研究较为缺乏。因此,本文参照现有文献的研究结果,对温度为近临界温度666 K下不同密度的超临界水体系进行分子动力学模拟,并增加更高温度的700与800 K这2个工况作为对照组,研究不同温度下超临界水的密度对其氢键数量、键能以及空间分布规律的影响,将有助于进一步理解超临界水密度不均匀性的微观机制。
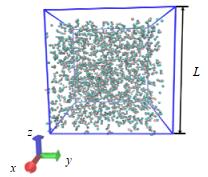
2 分子动力学模拟 2.1 模拟细节本研究采用经典的TIP4P/2005[11]作为水分子模型。如图 1所示为超临界水的初始分子建模示意图,其中红球表示氧原子,绿球表示氢原子,立方体的边长为L。所模拟的超临界水体系含1 000个水分子,不同密度下模型的L取值如表 1所示(ρ/ρc为超临界水密度与水临界密度的比值)。
|
图 1 超临界水的初始分子建模 Fig.1 Initial molecular model of supercritical water |
|
|
表 1 超临界水模型的边长取值 Table 1 Side length values of the supercritical water model |
分子动力学模拟使用的平台是LAMMPS,采用的力场为TIP4P力场,并设置三维周期性边界条件(PPP)。温度与压力的控制采用Nose-Hoover耦合方法,并采用PPPM算法计算静电相互作用力。初始分子速度由高斯随机分布决定。库伦截断半径与范德华力截断半径均为1 nm。根据相关文献中对水分子进行模拟的经验,模拟的时间步长设为10-15 s,每隔10-12 s保存坐标数据。在正则系综(即NVT系综)下进行模拟,系统先运行2×10-9 s达到平衡态,再计算10-9 s进行数据分析。如上所述,为揭示不同温度的影响,系统的温度设定为666、700、800 K。
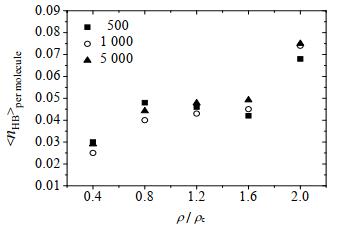
2.2 模型检验为了对模拟体系的分子数量无关性进行检验,首先计算了温度为666 K时分子数分别为500、1 000与5 000的3个超临界水体系中的平均氢键数随密度的变化关系。如图 2所示,3个体系模拟得到的平均氢键数(< nHB > per molecule)随密度比值的变化规律完全一致,体系分子数的变化对模拟结果影响不大,相对偏差在20%以内。因此,为了相对节约计算资源,本研究的后续模拟中均选取水分子数为1 000来构建模拟体系。
|
图 2 不同水分子数超临界水体系中平均氢键数随密度的变化 Fig.2 Variation of average number of hydrogen bonds as a function of density in supercritical water systems with different water molecule numbers |
对模拟得到的超临界水的自扩散系数与文献中的实验值[12]以及前人的分子动力学模拟结果(采用256个水分子,温度为666 K)[8]进行对照,以检验本文所建立的超临界水模型的可靠性。采用Einstein法[13]计算超临界水的自扩散系数。该方法的基本原理是通过统计粒子均方根位移与运动时间的关系,当时间足够长二者呈线性关系时取其斜率的1/6即为自扩散系数,其公式如下所示:
| $ {D_s} = \mathop {{\rm{lim}}}\limits_{t \to \infty } \frac{1}{{6{N_t}}}\left( {\sum\limits_{i = 1}^N | {r_i}(t) - {r_i}(0){|^2}} \right) $ | (1) |
式中:N为粒子数目,t为运动时间,ri(t)为粒子瞬时位置,ri(0)为粒子初始位置。
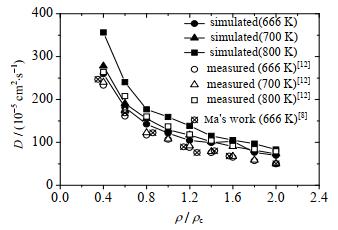
实验值由LAMB等[12]的实验数据插值计算得到。如图 3所示,本文的模拟值与实验值和前人的模拟值均吻合较好,总体偏差率低于15%。在保持温度不变的条件下,超临界水的自扩散系数D随密度比值升高而减小至趋于平缓。这是由于密度增大,分子间的碰撞概率增大,且氢键数量增加,进一步阻碍了分子扩散,传质能力减弱,从而表现为自扩散系数减小。在ρ > 1.2 ρc时自扩散系数的变化低于10%,与MA等[8]在ρ > 1.25 ρc时发现的密度对自扩散系数影响很小的结果基本一致。800 K超临界水自扩散系数最高,666 K最低,且随着温度的降低自扩散系数也逐渐减小,是由于温度升高促进了水分子的热运动,且氢键作用减弱,水分子运动的空间位阻效应减弱[14],传质能力增强。
|
图 3 超临界水自扩散系数随密度的变化 Fig.3 Variation of self-diffusion coefficient of supercritical water as a function of density |
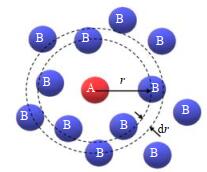
如图 4所示为径向分布示意图,通常用来描述局部粒子的分布,其表达式如下所示:
|
图 4 径向分布示意图 Fig.4 Schematic diagram of radial distribution |
| $ {g_{{\rm{AB}}}}(r) = \frac{{{\rm{d}}{n_{\rm{r}}}}}{{4\pi {r^2}{\rho _{\rm{B}}}{\rm{d}}r}} $ | (2) |
式中:dnr为半径从r到r+dr球壳内围绕每个A粒子周围B粒子的数目,ρB为B粒子的数密度,r为距中心原子的半径,dr为球壳厚度。径向分布函数实际上是A粒子周围B粒子出现的概率密度函数,可通过其观测粒子的空间分布。由于每个水分子中只包含1个氧原子,因此可以通过观察氧氧径向分布函数来描述水分子的分布状况,即从gOO (r)峰值出现的位置,高度及曲线的走势来分析水分子的分布状况。因为水分子的分布状况的变化会影响氢键的分布状况,所以分析水分子分布对氢键分布的研究具有重要意义。
2.4 氢键特性表征本文使用几何标准定义氢键[6],从而对计算输出的坐标文件进行编程统计氢键的数量。如图 5所示,供体与受体氧原子距离rOO≤0.36 nm,供体与受体氧原子与形成氢键的氢原子夹角∠HOO≤30°且受体氧原子与氢原子距离rOH≤0.24 nm可视为形成氢键。

|
图 5 氢键几何模型 Fig.5 Geometric model of hydrogen bonds |
氢键键能仅由3个原子(OD -H...OA)的短程库仑作用决定:
| $ {E_{{\rm{HB}}}} = \frac{{{k_{\rm{B}}}{q_{\rm{O}}}^2}}{{{r_{{\rm{DA}}}}}} + \frac{{{k_{\rm{B}}}{q_{\rm{O}}}{q_{\rm{H}}}}}{{{r_{{\rm{HA}}}}}} $ | (3) |
式中:qO和qH分别为氧原子和氢原子所带的电荷量,单位为1.6×10-19 C;rDA表示氢键供体与受体水分子中氧原子之间的距离,单位为10-10 m;rHA表示氢原子与受体氧原子之间的距离,定义为氢键键长,单位为10-10 m; kB为玻尔兹曼常数,其值为(1.380 658±0.000 012)×10-23 J·K-1。
| $ {\rm{平均氢键键能为}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\bar E_{{\rm{HB}}}} = \frac{1}{{{n_{{\rm{HB}}}}}}\sum\limits_{i = 1}^{{n_{{\rm{HB}}}}} {{E_{{\rm{HB}}}}} (i) $ | (4) |
式中:EHB为平均氢键键能,nHB为氢键数量,EHB(i)为第i个氢键的键能。水分子平均氢键数为
| $ < {n_{{\rm{HB}}}}{ > _{{\rm{ per molecule }}}} = \frac{{{n_{{\rm{HB}}}}}}{{{N_{{\rm{ water }}}}}} $ | (5) |
式中:nHB为氢键数量,Nwater为体系水分子数量。
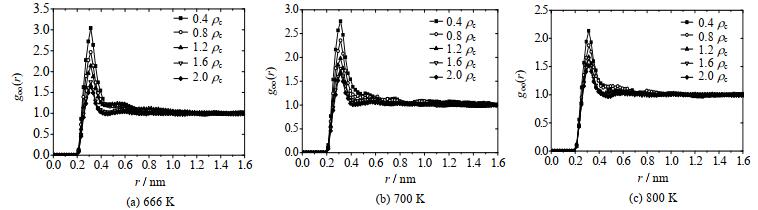
3 模拟结果及讨论 3.1 水分子的空间分布由于每个水分子只含有一个氧原子,因此可以通过计算氧氧径向分布来分析水分子的空间分布情况。不同密度超临界水中的氧氧径向分布模拟结果如图 6所示。
|
图 6 超临界水中的氧氧径向分布 Fig.6 Radial distribution of oxygen-oxygen in supercritical water |
根据NVT系综下分子运动轨迹文件,计算了在666,700与800 K温度下的不同密度的氧氧原子的径向分布函数。由图 6可知,超临界水gOO(r)的第1个峰均位于0.29 nm,说明超临界条件下水分子之间出现概率最高为0.29 nm。第2峰基本消失,说明在超临界条件下氢键作用变得很弱。在恒温条件下,gOO(r)的第1峰高度具有密度依赖性,且随着密度的减小,第1峰高度增大,说明超临界水短程有序性随密度减小而增大,在较低密度的条件下会形成局部团聚现象。水分子的局部团聚会导致氢键在空间分布上呈现局部团聚的现象。但随着温度升高,由于分子热运动增强,这种密度依赖性减弱,且第1峰高度减小,这与SOPER等[15]的研究结论一致。
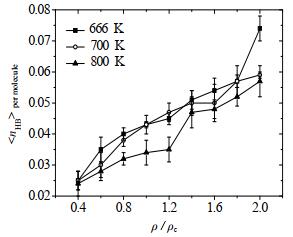
3.2 氢键数量与平均键能水分子平均氢键数(< nHB > per molecule)与密度比值的关系如图 7所示。值得注意的是,图中给出了在若干次模拟中所得到数据点的误差波动情况以说明模拟数据的可重复性。由于使用了NVT系综,因此在模拟过程中存在体系温度的随机波动现象,从而导致模拟结果也会出现一定的随机波动。在温度不变的情况下,水分子平均氢键数随密度增加而增加,这是由于水分子密度增大,结构更紧凑,水分子之间更容易形成氢键。但当ρ > 1.4ρc时平均氢键数趋于平缓,密度的影响减小。超临界水在666 K下平均氢键数最少,800 K时最多。这是由于水分子的热运动增强导致更难达到成键的几何条件。因此,随着温度的升高,氢键的作用减弱。在666 K温度下,平均氢键数在密度为2.0ρc时的平均氢键数较高,可能是因为在较低温度下氢键的密度依赖性更大,高密度时更容易出现团聚现象。
|
图 7 超临界水中氢键数量随密度的变化 Fig.7 Variation of hydrogen bond number as a function of density in supercritical water |
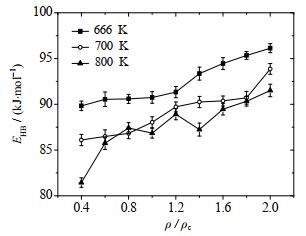
平均氢键键能EHB与密度比值的关系如图 8所示。在温度一定的条件下,超临界水平均氢键键能随着密度比值增大有上升的趋势,其中温度为666 K时平均氢键键能在2.0 ρc相比0.4 ρc增加了7.0%,温度为700 K时增加了9.1%,温度为800 K时增加了12.3%。氢键键能增长幅度随温度升高而增加,总体增长幅度较为平缓。这是因为密度增大导致水分子之间距离更近,形成的氢键更稳定,键能更大。在温度为800 K的条件下,超临界水平均氢键键能则波动最大,可能是由于水分子热运动较强,使得原子之间的距离有很大的随机性;在温度为666 K的条件下,平均氢键键能总体最高,且随和温度的上升而下降,这是因为温度更低的条件下分子间距离更小,导致氢键键能更大。
|
图 8 超临界水中平均氢键键能随密度的变化 Fig.8 Variation of average hydrogen bond energy as a function of density in supercritical water |
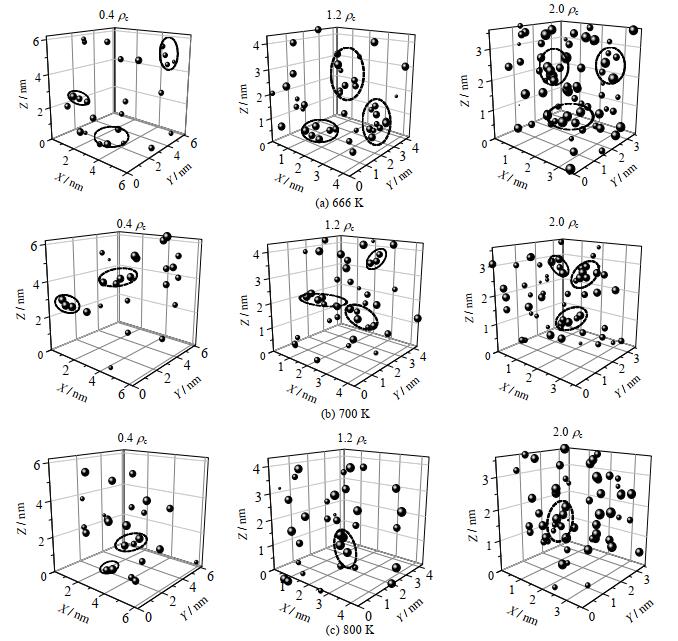
如图 9所示以受体氧原子坐标为氢键坐标,氢键键能大小表现在圆球的大小上。温度不变时,随着密度的增大,氢键成键在空间分布上更均匀,团聚现象(图中黑色虚线所示)越少,密度增大与氢键更均匀的分布使得水分子的传质能力降低,表现在自扩散系数的减小。高密度超临界水体系中心处平均氢键键能大小更高(圆球更大),成键更稳定。在密度不变的条件下,氢键空间分布随着温度的升高而变得更加均匀,即更难出现团聚现象。同时,在更高温度的情况下,氢键数目更低,氢键键能大小差异更小。
|
图 9 不同密度(0.4 ρc,1.2 ρc,2.0 ρc)超临界水中氢键的空间分布 Fig.9 Spatial distribution of hydrogen bonds in supercritical water having different densities (0.4 ρc, 1.2 ρc, 2.0 ρc) |
本文采用分子动力学模拟方法分析了温度为666,700与800 K的超临界水在不同密度下(0.4 ρc~2 ρc)的氢键特性及其空间分布与密度的关系,得出以下主要结论:
(1) 超临界水中的氢键数量随其密度的增大而增加,但在ρ > 1.4ρc时氢键数量的增长较为平缓;在较高的温度下氢键数量也较少。
(2) 超临界水中氢键的平均键能随其密度的增大而增大。当温度升高时,平均氢键键能变小,但其随密度变化的波动性变得更大。
(3) 超临界水中氢键的成键空间均匀性随密度的增大而增加,且随温度的升高而增加。密度较低时,超临界水更易形成局部团聚现象,导致氢键在空间分布上也呈现局部团聚;而密度较高时,超临界水体系在几何中心处的氢键成键更稳定。
| [1] |
潘志彦, 林春绵, 周红艺, 等. 乙酸在超临界水中氧化分解的动力学研究[J]. 高校化学工程学报, 2003, 17(1): 101-105. PAN Z Y, LIN C M, ZHOU H Y, et al. Oxidative degradation kinetics of acetic acid in the supercritical water[J]. Journal of Chemical Engineering of Chinese Universities, 2003, 17(1): 101-105. DOI:10.3321/j.issn:1003-9015.2003.01.019 |
| [2] |
丁军委, 陈丰秋, 吴素芳, 等. 苯胺在超临界水中氧化反应动力学的研究[J]. 高校化学工程学报, 2001, 15(1): 66-70. DING J W, CHEN F Q, WU S F, et al. Kinetics of aniline oxidation in supercritical water[J]. Journal of Chemical Engineering of Chinese Universities, 2001, 15(1): 66-70. DOI:10.3321/j.issn:1003-9015.2001.01.013 |
| [3] |
关宇, 裴爱霞, 郭烈锦. 纤维素在超临界水中的催化气化制氢研究[J]. 高校化学工程学报, 2007, 21(3): 436-441. GUAN Y, PEI A X, GUO L J. Hydrogen production by catalytic gasification of cellulose in supercritical water[J]. Journal of Chemical Engineering of Chinese Universities, 2007, 21(3): 436-441. DOI:10.3321/j.issn:1003-9015.2007.03.013 |
| [4] |
肖吉, 陆九芳, 陈健, 等. 超临界水中气体扩散系数的分子动力学模拟[J]. 高校化学工程学报, 2001, 15(1): 6-10. XIAO J, LU J F, CHEN J, et al. Molecular dynamics simulation for diffusion coefficients of gases in supercritical water[J]. Journal of Chemical Engineering of Chinese Universities, 2001, 15(1): 6-10. DOI:10.3321/j.issn:1003-9015.2001.01.002 |
| [5] |
SKARMOUTSOS I, SAMIOS J. Local density inhomogeneities and dynamics in supercritical water: A molecular dynamics simulation approach[J]. Journal of Physical Chemistry B, 2006, 110(43): 21931-21937. DOI:10.1021/jp060955p |
| [6] |
SKARMOUTSOS I, DELLIS D, SAMIOS J. The effect of intermolecular interactions on local density inhomogeneities and related dynamics in pure supercritical fluids. A comparative molecular dynamics simulation study[J]. Journal of Physical Chemistry B, 2009, 113(9): 2783-2793. DOI:10.1021/jp809271n |
| [7] |
LIU K, CRUZAN J D, SAYKALLY R J. Water Clusters[J]. Science, 1996, 271(5251): 929-933. DOI:10.1126/science.271.5251.929 |
| [8] |
MA H, MA J. Density dependence of hydrogen bonding and the translational-orientational structural order in supercritical water: A molecular dynamics study[J]. Journal of Chemical Physics, 2011, 135(5): 1-8. |
| [9] |
SKARMOUTSOS I, GUARDIA E, SAMIOS J. Local structural fluctuations, hydrogen bonding and structural transitions in supercritical water[J]. Journal of Supercritical Fluids, 2017, 130: 156-164. DOI:10.1016/j.supflu.2017.08.004 |
| [10] |
SAHLE C J, STERNEMANN C, SCHMIDT C, et al. Microscopic structure of water at elevated pressures and temperatures[J]. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110(16): 6301-6306. DOI:10.1073/pnas.1220301110 |
| [11] |
JORGENSEN W L, CHANDRASEKHAR J, MADURA J D, et al. Comparison of simple potential functions for simulating liquid water[J]. Journal of Chemical Physics, 1998, 79(2): 926-935. |
| [12] |
LAMB W J, HOFFMAN G A, JONAS J. Self‐diffusion in compressed supercritical water[J]. Journal of Chemical Physics, 1981, 74(12): 6875-6880. DOI:10.1063/1.441097 |
| [13] |
ALLEN M P, TILDESLEY D J, BANAVAR J R. Computer simulation of liquids[M]. England: Clarendon Press, 1989.
|
| [14] |
WANG G, WANG X, ZHANG Y F, et al. Study on the effect of hydrogen bonds on sieving effects of nanofiltration process[J]. Journal of Environmental Science and Engineering, 2009, 3(12): 43-46. |
| [15] |
SOPER A K. The radial distribution functions of water and ice from 220 to 673 K and at pressures up to 400 MPa[J]. Chemical Physics, 2000, 258(2): 121-137. |




