1 前言

煤气化技术是实现煤炭清洁高效利用的重要途径。对煤气化过程的优化，可以挖掘和提升气化装置生产潜能，对工业实际应用具有重要意义。Aspen Plus^[1-2]和Fluent等仿真软件^[3-4]常用于煤气化反应过程研究，但其高精度寻优过程却是计算昂贵的问题。目前，代理模型辅助进化算法(surrogate-assisted evolutionary algorithms，SAEAs)已经广泛用于昂贵问题优化中，在化工过程仿真模拟优化中逐渐被研究者关注^[5]。基于代理模型的优化，训练样本点选取是一个关键因素。因此，在有限计算成本下采样策略的构建成为SAEAs的研究重点。

最简单、直接的采样策略是选择当前代理模型预测的最好解加入训练数据集^[6]，改善当前最优解的精度，也就是局部开发^[7]。局部开发的采样准则更多集中在局部区域寻找最优解，如采用信赖域法^[8]、序列二次规划法^[9]等。另一种采样策略是全局探索，通过搜寻未探索区域选择当前代理模型的最不确定点，跳出局部最优，有效提高代理模型精度^[7]。在最不确定的样本点选择中，常以均方误差(mean squared error, MSE)^[10-11]、采样点和已知点之间距离函数^[12-15]最大为目标选择采样点。Xu等^[16]基于Voronoi图，根据误差和距离选择样本点，对低维度(维度d≤10)问题获得较好的最优解。Wang等^[17]基于委员会的主动学习方法，以不同代理模型之间预测偏差最大的样本点作为最不确定的点，有效地解决了复杂高维问题(d=20，30)，但在低维度问题(d=10)上不具优势。

为了在有限的精确函数评价(function evaluations, FEs)内获得更好的最优解，本文提出了基于交叉验证和Voronoi图的代理辅助进化算法(cross validation Voronoi surrogate-assisted evolutionary algorithm, CVVSAEA)。CVVSAEA通过留一交叉验证(leave-one-out cross validation, LOOCV)和Voronoi图选择不确定性较高的样本点，采用全局集成模型和局部代理模型辅助粒子群优化(particle swarm optimization, PSO)算法寻优。通过对中等规模复杂问题的测试说明了本文方法的有效性，并将其应用到煤气化过程中。

2 代理模型及PSO算法 2.1 代理模型

常用的代理模型有Kriging^[18]、径向基函数(radial basis function, RBF)^[8]、多项式回归响应面(polynomial regression surface, PRS)、支持向量回归以及多个单独代理模型构成的集成代理模型^[17]。Kriging模型是一种采用插值方法的无偏估计模型，除了可以预测某一特定点处的值外，还可以预测方差，方差可以作为一种不确定性衡量。RBF是一种采用多变量数据插值方法的模型，通过基函数加权求和近似函数，具有较好的局部逼近能力。

不同的代理模型适用于求解不同特性的问题，集成代理模型可以弥补单个代理模型的缺点，更有效解决复杂黑箱优化问题^[11]。集成代理模型一般采用单个代理模型权重求和的方法建立，其形式如下^[7]：

$\widehat y(\mathit{\boldsymbol{x}}) = \sum\limits_{k = 1}^M {{\omega _k}(\mathit{\boldsymbol{x}}){{\widehat y}_k}(\mathit{\boldsymbol{x}})} $

(1)

式中：ɷ_k(x)为第k个代理模型的权值，且满足$\sum\nolimits_{k = 1}^M {{\omega _k}(\mathit{\boldsymbol{x}}) = 1} $，M为单个代理模型个数；${\widehat y_k}(\mathit{\boldsymbol{x}})$为第k个代理模型的预测值。ɷ_k(x)是集成代理模型构造的关键，可以根据交叉验证的误差确定^[19]。

Kriging模型和RBF模型适合多模态问题，PRS模型具有较好的全局近似趋势。因此，本文选用Kriging、RBF、PRS构成集成模型，力图在全局优化中把精度的损失降到最低。

2.2 PSO算法

PSO算法由于其简单且寻优能力强在工程优化设计领域中得到了广泛应用^[17]。本文采用一种具有惯性权重因子的改进PSO算法，粒子每代的速度v^g和位置x^g更新公式如下^[17]：

${\mathit{\boldsymbol{x}}^{g + 1}} = {\mathit{\boldsymbol{x}}^g} + {\mathit{\boldsymbol{v}}^{g + 1}}$

(2)

${\mathit{\boldsymbol{v}}^{g + 1}} = {\omega _g}{\mathit{\boldsymbol{v}}^g} + {c_1}{r_1}({\mathit{\boldsymbol{x}}_{{\rm{pbest}}}} - {\mathit{\boldsymbol{x}}^g}) + {c_2}{r_2}({\mathit{\boldsymbol{x}}_{{\rm{gbest}}}} - {\mathit{\boldsymbol{x}}^g})$

(3)

式中：x_pbest为单个粒子最好解；x_gbest为整个群体中所有粒子的最好解；g为当前迭代代数；r₁和r₂为[0, 1]的随机数；c₁和c₂为学习因子，这里参照Wang等^[17]数据，取c₁=c₂=1.494 45。ɷ_g为惯性权重因子，这里ɷ_g从0.9到0.4之间随着迭代代数g线性下降，具体形式如下^[20]：

${\omega _g} = 0.9 - 0.5\frac{g}{{{g_{\max }}}}$

(4)

式中：g_max为最大迭代代数。

3 CVVSAEA的采样策略

以基于委员会主动学习的代理模型辅助粒子群优化(committee-based active learning for surrogate-assisted particle swarm optimization, CAL-SAPSO)^[17]为基本框架，本文分别从寻找最不确定点、全局最优点、局部最优点3个方面选择样本点，在全局搜索和局部搜索之间进行采样准则转换。

假设已知样本点X=[x₁, …, x_i, …, x_t]^T，x_i∈${\mathbb{R}^d}$，d为每个样本x_i的维度，t为当前集合中样本个数，对应精确函数值Y=[y(x₁), …, y(x_i), … y(x_t)]^T =[y₁, …, y_i, …, y_t]^T，构成了训练数据集(X, Y)_t={(x₁, y₁), …, (x_i, y_i), … (x_t, y_t)}^T。

3.1 最不确定点x^U选取

(1) 方差最大点x_σmax的确定

模型预测精度的提高，很大程度取决于对整个设计空间中不确定性区域的探索。采用LOOCV方法判断已知样本点附近不确定性程度，样本点x_i的LOOCV方差计算如式(5)：

${\widehat \sigma _i} = \frac{1}{{t - 1}}\sum\limits_{i = 1}^{t - 1} {{{(y({\mathit{\boldsymbol{x}}_i}) - {{\widehat y}_{\mathit{\boldsymbol{x}}\backslash {\mathit{\boldsymbol{x}}_i}}}({\mathit{\boldsymbol{x}}_i}))}^2}} $

(5)

式中：y(x_i)表示样本点x_i的实际函数值；${\widehat y_{\mathit{\boldsymbol{x}}\backslash {\mathit{\boldsymbol{x}}_i}}}({\mathit{\boldsymbol{x}}_i})$表示已知点集合中除了样本点x_i外，其他(t-1)个样本点构建的代理模型预测x_i的函数值。

方差最大点x_σmax具有最大的不确定性，x_σmax周围的点相对其他区域也应具有较大的不确定性。在x_σmax周围选择点加入已知样本中，则会极大地提高模型的精度。采用Kriging模型预测，其相关函数选择常用的高斯函数。

(2) 空间分割和x_σmax区域的界定

根据Voronoi图方法，由设计空间中任意两个已知样本点垂直平分线为界把整个设计空间分割成t个单元{C₁, C₂, ⋯, C_t}，每个C_i包含一个已知点x_i^[16]。对于多维问题，如果要精确计算出形状不规则的单元C_i的边界，需要比较复杂的计算过程。采用Monte Carlo方法可以简单有效地对Voronoi图中各个单元进行分割，近似确定单元C_i的边界范围^[16]。

首先，在整个设计空间内，产生大量均匀分布随机点x_r，数量为N=t×d×ω_r，ω_r为随机点生成数量的权值；把x_r归入距离最近已知点x_i的单元C_i中，由包含x_σmax点的单元C_σmax中所有随机点近似描述单元边界。C_σmax中随机点相对其他单元具有较大方差，在其单元内选取采样点可以提高模型近似精度。

(3) 采样点x^U选择

单元C_σmax内的随机点x_r在模型构建上具有和x_σmax相似的影响作用，直接从这些随机点中选取采样点更加简单有效。为了增加采样点的多样性，在单元C_σmax内选择距离x_σmax最远的随机点。为了提高模型的近似精度，还要考虑模型预测的偏差大小。因此，建立了以距离和偏差为目标的函数f ^U(x_r)，

${f^{\rm{U}}}({\mathit{\boldsymbol{x}}_{\rm{r}}}) = \left\{ {\left\| {{\mathit{\boldsymbol{x}}_{\rm{r}}} - {\mathit{\boldsymbol{x}}_{{\rm{ \mathsf{ σ} }}\max }}} \right\|_{{\rm{norm}}}^2 \times (\widehat y({\mathit{\boldsymbol{x}}_{\rm{r}}}) - y({\mathit{\boldsymbol{x}}_{{\rm{ \mathsf{ σ} }}\max }}))_{{\rm{norm}}}^2} \right\}$

(6)

式中：x_r为单元C_σmax内的随机点，$\widehat y({\mathit{\boldsymbol{x}}_{\rm{r}}})$为代理模型预测x_r的函数值，为了减少距离差和函数值差范围不同的影响，对求得差值分别进行最大最小归一化处理，norm表示归一化处理。

满足maxf ^U (x)的解x即为最不确定的采样点x^U。x^U描述如下：

${\mathit{\boldsymbol{x}}^{\rm{U}}} = \mathop {\arg \max }\limits_\mathit{\boldsymbol{x}} {f^{\rm{U}}}({\mathit{\boldsymbol{x}}_{\rm{r}}})$

(7)

x^U选取流程如图 1所示。

3.2 当前全局最优点x^Gb选取

全局模型采用Kriging、RBF、PRS构成集成代理模型${\widehat y_{\rm{G}}}(\mathit{\boldsymbol{x}})$。根据LOOCV的误差，获得各个代理模型的权值^[21]。权值ω_k (x)形式为

${\omega _k}(\mathit{\boldsymbol{x}}) = \frac{{\frac{1}{{{E_k}(\mathit{\boldsymbol{x}})}}}}{{\sum\limits_{j = 1}^M {\frac{1}{{{E_j}(\mathit{\boldsymbol{x}})}}} }}$

(8)

式中：E_k(x)为第k个代理模型交叉验证的均方根误差。

通过PSO算法找到$\min {\widehat y_{\rm{G}}}(\mathit{\boldsymbol{x}})$的当前全局最优点x^Gb，其描述为

${\mathit{\boldsymbol{x}}^{{\rm{Gb}}}} = \mathop {\arg \min }\limits_\mathit{\boldsymbol{x}} {\widehat y_{\rm{G}}}(\mathit{\boldsymbol{x}})$

(9)

3.3 局部最优点x^Lb选择

随着算法迭代，样本点逐步向全局最优解趋近。当前训练集中函数值从小到大排序前top样本$(\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Y}})_t^\rm\rm{top}$会集中在一个局部区域，仅对局部区域进行搜索则会更快找到最优解。根据$(\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Y}})_t^\rm\rm{top}$中训练点建立局部代理模型${\widehat y_{\rm{L}}}(\mathit{\boldsymbol{x}})$，用PSO算法找到$\min {\widehat y_{\rm{L}}}(\mathit{\boldsymbol{x}})$的局部最优点x^Lb，其表示如下：

${\mathit{\boldsymbol{x}}^{{\rm{Lb}}}} = \mathop {\arg \min }\limits_{\mathit{\boldsymbol{x}} \in \left[ {\rm{l{b^\rm\rm{top}}, u{b^\rm\rm{top}}}} \right]} {\widehat y_{\rm{L}}}(\mathit{\boldsymbol{x}})$

(10)

式中：lb^top和ub^top为$(\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Y}})_t^\rm\rm{top}$中所有样本点的上下限范围。

3.4 搜索区域转换

为了平衡全局空间和局部空间的搜索，优化代理模型的采样策略常常在二者之间根据函数值是否改善、已知点距离是否过近、方差是否改善等准则自适应切换^[15]。本文中根据$\left|y^{\mathrm{sopt}}-y^{\mathrm{Cb}} | /\right| y^{\mathrm{Cb}} \mid>\varepsilon$，即函数值性能改善大于转换阈值ε则保持当前全局搜索或局部搜索不变，否则切换搜索区域。(x^sopt, y^sopt)代表本次搜索的最优数据点，y^Cb代表未加入(x^sopt, y^sopt)时训练数据集中的最好函数值。

3.5 CVVSAEA具体流程

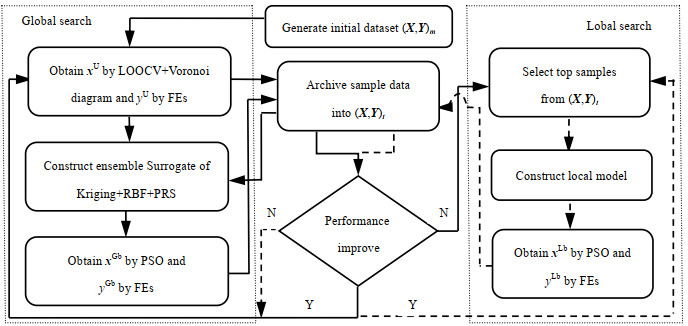
CVVSAEA流程图如图 2所示，具体步骤如下：

Step1：通过试验设计方法在设计空间中得到m个样本的初始数据集(X, Y)_m，设定最大函数评价次数t_max；

Step2：全局搜索

Step2.1：采用Kriging模型，通过LOOCV和Voronoi图，找不确定性较大区域，根据式(7)，选择出最不确定点x^U，并计算其精确函数值y^U，保存到当前数据集(X, Y)_t；

Step2.2：由已知数据集(X, Y)_t建立Kriging+RBF+PRS模型${\widehat y_{\rm{G}}}(\mathit{\boldsymbol{x}})$。根据式(9)，采用PSO算法找到全局最优点x^Gb，计算精确函数值y^Gb，保存到(X, Y)_t，根据函数性能改善情况进行全局搜索或者局部搜索；

Step3：局部搜索

Step3.1：当前数据集(X, Y)_t中样本点按照函数值从小到大排序，选择出排名前top的样本$(\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Y}})_t^\rm{top}$；

Step3.2：基于$(\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Y}})_t^\rm{top}$建立局部代理模型${\widehat y_{\rm{L}}}(\mathit{\boldsymbol{x}})$，根据式(10)，由PSO算法找到局部最优点x^Lb，计算其精确函数值y^Lb，保存到(X, Y)_t；根据转换准则进行全局搜索或者局部搜索；

当函数评价次数(即已知样本数)t≥t_max时，CVVSAEA停止搜索。

4 数值实例的实验结果及分析

为了验证所提出算法的性能，把CVVSAEA和先进的代理模型辅助优化算法CAL-SAPSO^[17]、代理模型加权平均法之一(one of the weighted average method，WTA1)^[19]、代理模型辅助进化策略之期望改进(metamodel assisted evolution strategies with expected improvement，MAES-ExI)^[22]进行了比较。

4.1 参数设置

本文采用拉丁超立方采样(latin hypercube sampling，LHS)生成初始样本点，取初始样本个数m = 5d。函数评价最大次数t_max=11d，作为整个算法终止条件。其中，随机点生成权值ω_r=100，全局和局部的转换阈值ε=1.0×10^-3，top=20%，局部代理模型采用RBF，其基函数为适合拟合复杂函数的多重二次函数。PSO算法中初始种群大小为100个，最大迭代次数为100代。为了保证公平性，PSO在其他的算法中设置相同。对广泛采用的5个函数维度d=10和d=20情况分别进行了测试，函数信息如表 1所示。

4.2 数值结果

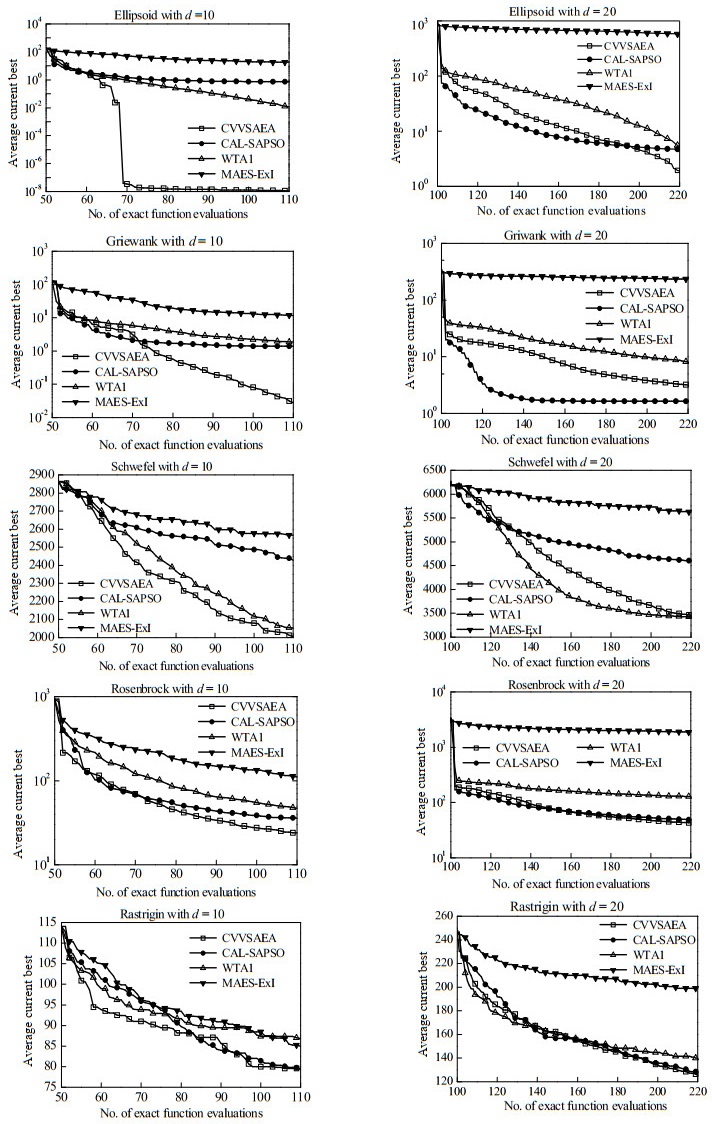
为了防止随机性，每个算法独立运行30次。CVVSAEA、CAL-SAPSO、WTA1、MAES-ExI算法的平均最好函数值及方差和平均运行时间如表 2所示，收敛曲线如图 3所示。由于前5d个FEs用于初始训练数据的评价，因此图中只从5d个FEs开始显示。

对表 2中的平均最好函数值进行了Friedman检验^[23]，p-value=7.9×10^-5 < 0.05，表明4种算法有显著差异。进一步采用Nemenyi后续检验^[23]比较各算法之间的差异，CVVSAEA性能明显好于MAES-ExI算法，同时CVVSAEA的平均序值也比CAL-SAPSO和WTA1好。

Ellipsoid函数是一个单模态问题。CVVSAEA性能最好，尤其是d = 10，基本得到了真实最优值0，远远好于其他算法。CVVSAEA采样策略更易跳出局部最优，比较适合解决单模态优化问题。Griewank函数是一个有很多规律分布局部极小点的多模态问题。在d = 10时，CVVSAEA明显好于其他算法。但在d = 20时，未能取得好于CAL-SAPSO的最优解。由于Griewank具有大量局部极小点，在非常有限训练数据下，建立的代理模型可能未能找到最优解附近足够的样本信息。Schwefel函数是一个典型的欺骗复杂问题，有很多局部极小值、全局最优值与最近的局部最小值距离很远，很难跳出局部最优。在d=10下，CVVSAEA好于其他3种算法，在d = 20下，略差于WTA1，但好于CAL-SAPSO和MAES-ExI。WTA1只从全局寻找最优解，不去探索不确定性和局部区域，因此具有更多全局搜索的机会。Rosenbrock函数是一个全局最优值位于一个狭长平滑抛物线形谷底的多模态问题。在d =10，d = 20条件下，CVVSAEA寻优性能最好，加入最不确定点和局部最优点的CVVSAEA、CAL-SAPSO比仅取全局最优点的WTA1更好。Rastrigin函数与Griewank函数有些相似，都是有很多规律分布的局部极小点，但它更复杂。在d =10下，CAL-SAPSO算法在搜索后期略超过CVVSAEA，得到更好的解。Rastrigin函数由于具有大量局部极小点，在有限次FEs内很难跳出局部最优，可能是ω_r略小未有效探索不确定点或者局部取top点有些过多造成的。随着维度增加在d = 20下，CVVSAEA寻优性能好于其他3个算法。除了F9外，采用集成模型的CVVSAEA、CAL-SAPSO以及WTA1均取得比仅用Kriging模型的MAES-ExI好的解。

总体来说，基于集成模型的采样策略具有更好的鲁棒性，最不确定样本点加入可以更好地提高模型精度，CVVSAEA的取点策略要好于其他3个算法。从表 2可以看出，在有限的FEs内CVVSAEA在10种情况下7次求得解最好，其余均排序在第2位；在运行时间方面，MAES-ExI算法虽然最快，但求得的优化解最差，CVVSAEA运行时间在d = 10时仅次于MAES-ExI算法，在d = 20总体略差于CAL-SAPSO算法。因此，综合考虑算法的求解精度和收敛速度，CVVSAEA具有更好的寻优性能。

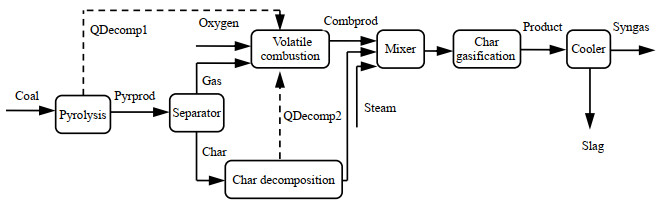
5 煤炭气化过程的优化

煤气化过程是通过煤炭与气化剂(水蒸气H₂O、CO₂、空气、O₂等)在高温下经过一系列复杂的物理化学过程，产生以CO、H₂等为主的清洁合成气的过程。工业上常见的气化炉有Lurgi炉、英国燃气Lurgi炉(British Gas-Lurgi，BGL)、高温温科勒(high temperature winkler，HTW)炉和Texaco炉等。气流床气化技术是目前煤气化技术发展的主要方向^[24-25]，本文以气流床煤气化炉Texaco为研究对象，CVVSAEA作为一种优化求解策略对其他气化炉同样适用。首先经过研磨，满足粒度要求的煤粉先与水混合成水煤浆，然后水煤浆和O₂同时从Texaco气化炉顶部喷入，依次发生煤热解、挥发分燃烧和焦炭气化反应，产生以CO和H₂为主的合成气，接着合成气和熔渣及未反应的碳离开反应区后进入炉子底部的激冷室，冷却后的合成气和饱和水蒸气从激冷室上部排出气化炉，熔渣经激冷固化后被分离出来最终进入渣罐，未反应的碳进入黑水处理系统。Texaco炉气化过程模拟流程如图 4所示。

在煤炭气化过程中，有效气产率是一个重要的评价指标，代表了单位质量的煤产出的有效气产量，有效气产率主要受气化原料组成及性质、进料量、氧煤比、蒸汽煤比、气化温度、气化压力等工艺参数影响。根据Texaco的Aspen Plus模型^[1]，以Illinois No.6煤为研究对象，气化压力维持在2 431 800 Pa不变，选取干煤粉进料流量及其温度、氧煤比和O₂温度、蒸汽煤比和水蒸气温度6个参数为操作变量，各个操作变量的取值范围根据文献[26]确定，最大化有效气(CO+H₂)产率为优化目标。采用LHS方法生成5d个初始样本点，调用Aspen Plus仿真模型计算其对应的有效气产率，得到初始训练数据集。仿真模型调用最大次数t_max=11d。随机点生成权值ω_r=100，转换阈值ε=1.0×10^-3，局部取函数值排序top=30%，局部代理模型采用Kriging，全局模型为Kriging+RBF+PRS。PSO算法初始种群为100个，最大迭代次数为100代。

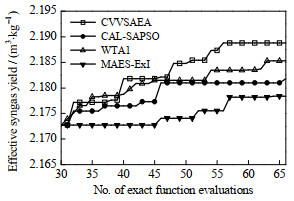
从图 5中可以看出，大约从第40次FEs开始，CVVSAEA找到的优化解开始好于其他3种算法，具有更好的寻优性能。分析表 3中数据，与其他3种算法相比，CVVSAEA使有效气产率分别提高了0.32%、0.16%、0.48%，对煤炭气化工业流程优化具有一定的应用价值和指导意义。

6 结论

基于LOOCV和Voronoi图，本文提出了一种选取最不确定点的采样准则优化代理模型，进而更加有效辅助进化算法解决其优化时计算昂贵问题。界定不确定性最高的区域，综合考虑多样性和性能指标选点，且无需进化算法求解，快速精准地改善了代理模型精度。采用集成模型预测具有更稳定的近似能力，选择较好点建立局部模型加快了收敛过程。全局搜索和局部搜索的自适应切换达到了平衡全局探索和局部开发的目的。通过不同模态不同维度下10个复杂测试问题和煤气化过程实例，发现在有限昂贵函数评价限制内，CVVSAEA具有更好的寻优性能，在煤气化过程优化中应用前景较好。尽管CVVSAEA在昂贵函数评价上有一定优势，但同时也存在一些不足。如问题维度过高时，Kriging模型计算成本较高，如何在高维问题下提高其计算效率是今后需要进一步深入研究的方向。

符号说明：