气液两相流动现象广泛存在于化工,石油,新能源、国防等诸多领域[1-4]。在实际生产过程中,设备内存在大量形状、大小、速度不同的气泡彼此影响,因此,研究气泡运动特性及气泡间的相互作用对于诸多工程领域均具有重要的价值和意义[5-8]。
MULLER等[9]对水下单气孔气泡生成特性进行可视化实验研究,发现在气体流速相对较大的情况,气泡尺寸随气体流速的增大而增大。ALADJEM等[10]对垂直管中2个连续气泡的相互作用进行实验研究,认为两气泡的运动特性主要由前行气泡决定。LIAO等[11]对多种不同位置关系的两气泡间相互作用的受力情况进行理论分析,并提出新的气泡聚并及破碎模型,ZUZANA等[12]对两气泡的碰撞过程进行实验研究,并建立的小气泡靠近大气泡时速度及轨迹的理论模型。朱恂等[13]对单孔气泡形成及运动特性进行可视化实验并发现气泡形成及运动过程可以分为生长、聚并、震荡和稳定4个阶段。马友光等[14]模拟双喷嘴气泡的生成上升及聚并过程,发现初始条件不同,会出现聚并、交替出现后聚并及先吸引再远离3种不同的气泡流型,张莹等[15]对水平布置等直径气泡上升过程进行数值模拟及分析,发现2个气泡上升运动时,气泡向两侧偏移逐渐分离。
以往针对气泡形成特性的研究主要集中在对单个气泡运动规律的研究,部分关于气泡碰撞、聚并的研究也主要是针对垂直共轴分布情况,对于水平分布气泡的上升过程及相互作用的研究则较少,尤其是关于外界条件,如孔口间距及直径等对气泡特性的影响的研究更是不足,因此,目前得到的研究结果及现象还不够丰富,仍需进一步研究,本文通过可视化实验研究双孔壁面孔口鼓泡行为,对两列气泡形成过程中的运动特性进行分析,通过与单孔气泡生成及运动特性的对比,分析孔口间距及孔口直径对气泡间相互作用的影响规律。
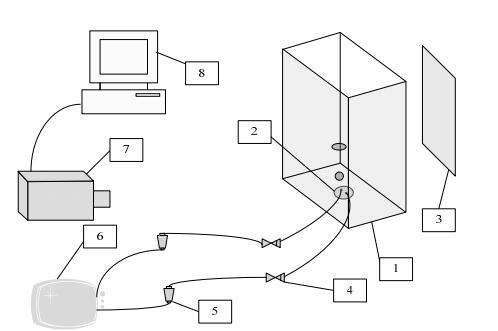
2 实验装置与实验方法 2.1 实验装置及系统如图 1所示为水下双气孔气泡生成特性实验系统示意图,实验装置由水箱、支架、浮子流量计、LED平面光源、气泡发生组件、止回阀、空气泵、高速摄像机、计算机组成。
|
图 1 实验装置示意图 Fig.1 Schematic diagram of the experimental setup 1. water tank 2. bubble generation module 3. LED plane light source 4. check valve 5. float flow meter 6. air pump 7. high-speed camera 8. computer |
可视化水箱为立方体透明容器,采用有机玻璃制成,尺寸为300 mm×300 mm×500 mm,拍摄方向尺寸为300 mm×300 mm,内盛液位高度为300 mm的纯净水,水箱底部开孔用来安装气泡发生组件,组件侧面加工出螺纹拧到水箱下部开孔处,方便根据实验需要更换不同的组件,如图 2所示,气泡发生组件由有机玻璃加工而成[16],组件上部有凸台,凸台高度为7 mm,直径为20 mm,根据实验需要在凸台上钻出不同的孔径,2个孔径相同,分别为do=1.5、2、2.5 mm 3种工况,双孔圆心间距分别为d=3、8、12 mm 3种工况。

|
图 2 气泡发生组件 Fig.2 Picture of the module for bubble generation |
气体由HP-1116电磁式振动空气流量泵提供,气泵额定电压220 V/50 Hz,额定功率15 W,最大排气量可达10 L·min-1。实验中选用的是LZB-3微小流量玻璃转子流量计,量程为16~160 mL·min-1,通过调节浮子流量计来控制进入气孔的气体流量。
采用高速摄像仪捕捉气泡的形成过程,拍摄时利用相机配套的PFV(Photron FASTCAM Viewer)软件进行相机参数的调整,为了拍摄到较为清晰地图像,实验中选择尺寸为300 mm×300 mm,额定功率12 W的LED平面光源对高速摄像仪进行补光,固定安装在与水箱拍摄面相对的一面,可以增强拍摄到的图像对比度。
2.2 图像处理及参数测量 2.2.1 图像处理方法本文采用Image-Pro Plus(IPP)软件对实验拍摄到的视频一帧一帧地进行处理。以气泡发生组件凸台直径20 mm作为标尺来测量气泡的几何参数尺寸,气泡在脱离时形状近似为球形,之后的运动过程中气泡表现为非对称的不规则形状,IPP软件可以自动识别与分离图像边缘区域,进行测量,极个别背景干扰严重情况,也可以手动识别图像边缘进行测量,测量内容包括坐标、距离、面积等。选取实验过程中的任意时刻的图像为例,如图 3所示,利用IPP得到的标尺及气泡的测量区域。

|
图 3 气泡脱离时选取的AOI Fig.3 Picture of AOI for bubble detachment |
气泡的大小、速度及其位置等是气泡在运输过程中的特性的关键参数。在实验过程中,高速摄影仪的拍摄速率是确定的,每帧图像的时间差便是已知的,由此,通过比较2帧图像中气泡的位置及其尺寸的差异,便可以得到气泡的特征参数,可以跟踪其运动轨迹、尺寸及速度变化规律等。
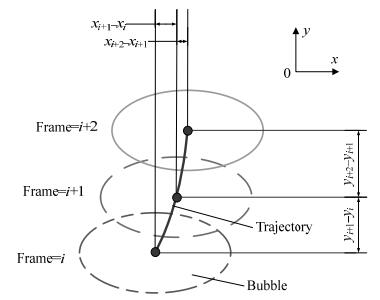
如图 4所示为3个相邻气泡的轮廓,其速度可以根据其在2个相邻帧中的质心位置和时间间隔计算:
| ${v_{x, i + 1}} = \frac{{{x_{i + 1}} - {x_i}}}{{\delta t}}$ | (1) |
| ${v_{y, i + 1}} = \frac{{{y_{i + 1}} - {y_i}}}{{\delta t}}$ | (2) |
|
图 4 气泡参数计算方法示意图 Fig.4 Schematic diagram of bubble parameter calculation |
式中:
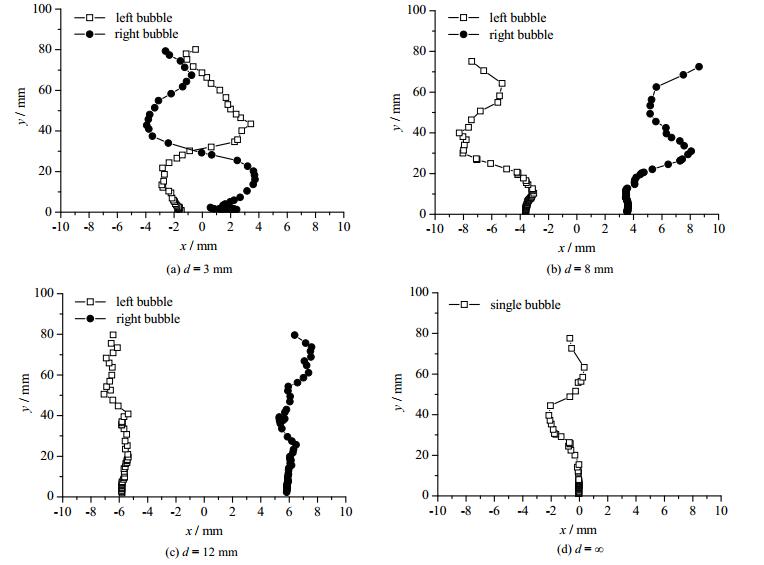
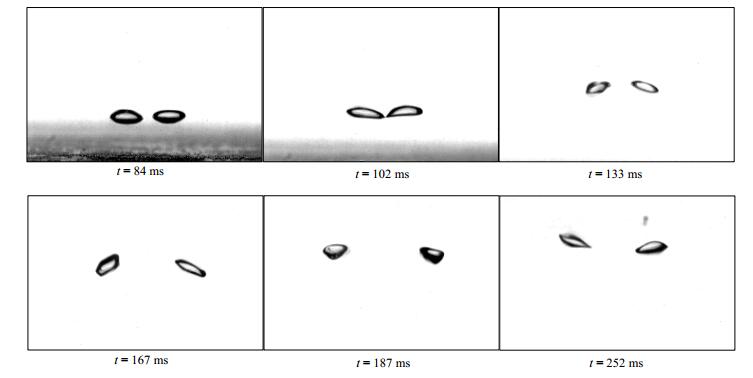
针对孔径为2 mm,气体体积流量为40 mL·min-1情况,分别拍摄孔间距为d=3、8、12 mm及单孔d=∞这4种工况,对气泡的上升过程进行追踪,得到3种工况的气泡上升轨迹,如图 5(a)、(b)、(c)所示,当两列气泡并排上升时,气泡间会相互影响,气泡上升轨迹并非直线型,而是上升同时会左右震荡,出现相互靠近—远离—再靠近的循环过程,在孔间距较小情况,上升过程中还会出现交叉现象。如图 6所示为孔径do = 2 mm、气体体积流量为40 mL·min-1、孔间距d = 8 mm实验工况所拍摄的图像数据,展示了2个同时脱离的气泡在上升过程中,其相对位置随时间的变化规律,可以发现2个气泡先靠近,当距离很小时,2个气泡又会逐渐分离,距离慢慢变大,当2个气泡相距较远时,2个气泡又会逐渐靠近。
|
图 5 气泡上升轨迹 Fig.5 Trajectory of bubble rising in the experiments |
|
图 6 气泡相对位置随时间变化规律 Fig.6 Relative positions of bubbles changing as a function of time |
同时从图 5(d)中可以看出,单列气泡的上升轨迹也并非完美的直线型,也存在很小幅度的左右震荡,与单孔工况气泡运动轨迹对比可以看出,当两列气泡上升时,孔间距越小,气泡上升时所伴随的左右震荡的振幅越大,孔间距越大,气泡左右震荡的幅度越小,气泡上升轨迹越接近单孔气泡的上升轨迹。
3.2 孔间距对气泡特性的影响当孔径均为2 mm时,对孔间距为d=3、8、12 mm及单孔4种情况进行不同流量的实验研究,提取不同工况下气泡脱离壁面时刻的直径,所得结果如图 7所示,其中,双孔气泡的脱离尺寸为左右2个气泡脱离尺寸的平均值,从图中可以看出,当气体体积流量qV位于40~120 mL·min-1时,气泡的脱离尺寸会随着气孔进气流量的增大而增大。
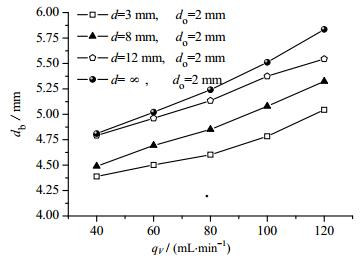
|
图 7 气泡脱离直径 Fig.7 Profiles of bubble detaching diameter |
对于双孔情况,孔间距的大小对气泡脱离尺寸也有明显的影响,若孔间距较小,气泡在生长过程便会相互影响,抑制彼此的成长,因此,如图 8所示,在孔径及气体体积流量均相同时,双孔情况下气泡的脱离尺寸会较单孔情况小,且孔间距越小,抑制效果越明显,双孔情况下气泡脱离尺寸与单孔情况气泡脱离尺寸的差值df会越大;df可由式(3)计算得出,在孔径及孔间距均相同时,气体流量越大,气泡脱离尺寸会越大,导致气泡在成长过程中相对距离会变小,彼此的抑制效应增强,脱离尺寸较单孔情况的差值会越大。
| ${d_{\rm{f}}} = {d_{\rm{b}}}_{{\rm{(s)}}} - {d_{\rm{b}}}_{{\rm{(t)}}}$ | (3) |
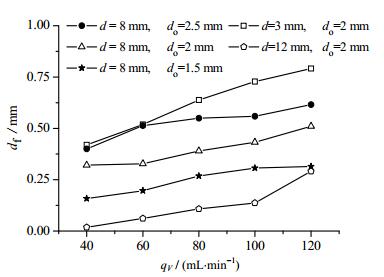
|
图 8 气泡脱离直径差值 Fig.8 Difference of bubble detaching diameters |
式中:db(s)为相同孔径相同流量时,单孔工况气泡脱离直径,db(t)为相同孔径相同流量时,双孔工况气泡脱离直径,df为相同孔径相同流量时,2种工况气泡脱离直径的差值。
图 9给出了不同的孔间距情况下气泡上升速度v随时间的变化规律,从图中可以发现,从整体趋势来看,气泡速度的变化趋势几乎相同,在气泡脱离后,都会有一个减速过程,在达到最小速度后,气泡上升速度会迅速增加,随后速度增长缓慢,最终气泡近似匀速上升。虽然不同孔间距工况气泡最终的稳定速度相差不大,但仍具有一定的规律性,即气体流量和孔径保持不变时,孔间距越小,气泡最终的稳定速度越小,对于单个的形状为球形的较小气泡的升运动,Stokes推导出了气泡上升的最终速度理论计算公式,根据Stokes理论,气泡最终速度与气泡尺寸有关,因此,孔间距越小,气泡脱离尺寸会变小,从而导致气泡最终速度变小。
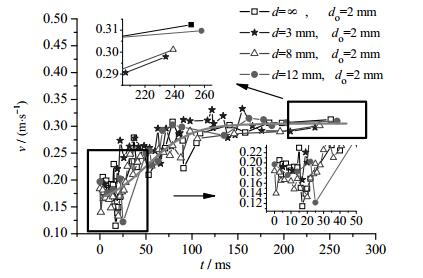
|
图 9 气泡运动速度随时间变化 Fig.9 Velocity variation as a function of time under different conditions |
气泡上升过程中会伴随形变特性,导致气泡会有一部分能量在变形能及动能间转换,从而出现气泡速度整体呈增加趋势的同时,伴随有一定的速度波动的现象。
3.3 孔径尺寸对气泡特性的影响当孔间距均为8 mm时,对孔径为do=1.5、2、2.5 mm 3种情况进行不同流量的实验研究,提取不同工况下气泡脱离壁面时刻的直径,所得结果与相同孔径单孔情况下的实验结果进行对比,如图 10所示,气泡的脱离直径db会随着气孔进气流量及孔径尺寸的增大而增大,且从图 10可以看出,当孔间距d相同相时,孔径越大,脱离尺寸的差值df会越大,这是因为孔径越大,产生的气泡越大,即使孔间距保持不变,气泡质心距离不变,但气泡间的最小距离会变小,两气泡的影响增强,从而导致df变大。
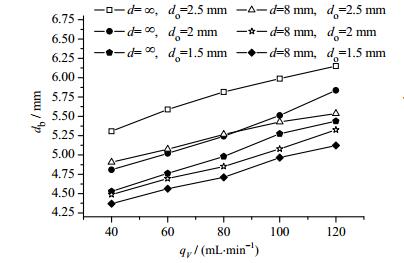
|
图 10 气泡脱离直径 Fig.10 Profiles of bubble detaching diameter |
如图 11所示为不同孔径情况下气泡上升速度随时间的变化规律,从图中可以发现,气泡速度的变化趋势与前文3.2节所描述的趋势是相同的。当气体流量和孔间距保持不变时,孔径越小,气泡最终的稳定速度越小,根据Stokes等提出的理论,气泡最终速度与气泡尺寸有关,孔径越小,气泡脱离尺寸会变小,因此会导致气泡最终速度变小。
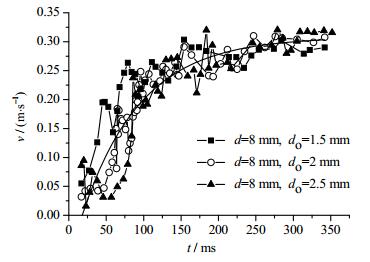
|
图 11 气泡运动速度随时间变化 Fig.11 Velocity variation with time under different conditions |
文中对不同孔径及孔间距的气泡发生组件进行了不同流量的可视化实验研究,通过分析孔径及孔间距对气泡运动轨迹、气泡脱离直径、速度变化规律的影响规律,可以得出如下结论:
(1) 2列气泡并排上升时的轨迹并非直线型,且2个气泡之间距离并不会保持恒定,而是会出现“相互靠近—远离—再靠近”的循环震荡过程,孔间距越小,气泡上升时所伴随的左右震荡的振幅越大。
(2) 在孔径及气体流量均相同时,双孔情况下气泡的脱离尺寸会较单孔情况小,且孔间距越小,脱离尺寸的差值会越大,气泡最终的稳定速度越小;在孔径及孔间距均相同时,气体流量越大,气泡脱离尺寸较单孔情况的差值会越大。
(3) 孔间距相同,气体流量相同,孔径越大泡的脱离尺寸越大,脱离尺寸与单孔情况的差值越大,气泡最终的稳定速度越大。
| [1] |
PAINMANAKUL P, LOUBIERE K, HEBRARD G, et al. Study of different membrane spargers used in waste water treatment: characterisation and performance[J]. Chemical Engineering Process, 2004, 43(11): 1347-1359. DOI:10.1016/j.cep.2003.09.009 |
| [2] |
张志友, 金良安, 何升阳, 等. 气泡上浮运动与传热传质的耦合模型[J]. 高校化学工程学报, 2018, 32(2): 358-367. ZHANG Z Y, JIN L A, HE S Y, et al. Study on coupling models for bubble floatation accompanied with heat and mass transfer[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(2): 358-367. DOI:10.3969/j.issn.1003-9015.2018.02.014 |
| [3] |
温宇, 朱春英, 付涛涛, 等. 不等宽T型分岔微通道内气泡的体积分配规律及关联[J]. 高校化学工程学报, 2016, 30(1): 19-25. WEN Y, ZHU C Y, FU T T, et al. Volume distribution and correlation of bubbles in a microfluidic T-junction with unequal width bifurcations[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(1): 19-25. DOI:10.3969/j.issn.1003-9015.2016.01.004 |
| [4] |
LAU R, MO R, BEVERLY S W S. Bubble characteristics in shallow bubble column reactors[J]. Chemical Engineering Research and Design, 2010, 88(2): 197-203. DOI:10.1016/j.cherd.2009.07.008 |
| [5] |
RIBEIRO C P J R, LAGE P L C. Experimental study on bubble size distributions in a direct-contact evaporator[J]. Brazilian Journal Chemical Engineering, 2004, 21(1): 69-81. |
| [6] |
谢育博, 刘道平, 杨亮, 等. 蒸馏水和自来水中悬浮气泡表面天然气水合物生长特性的实验研究[J]. 化工进展, 2017, 36(1): 129-135. XIE Y B, LIU D P, YANG L, et al. Experimental study on the growth characteristics of natural gas hydrate formation on suspended gas bubbles in distilled water and tap water[J]. Chemical Industry and Engineering Progress, 2017, 36(1): 129-135. |
| [7] |
李希, 李兆奇, 管小平, 等. 气液鼓泡塔流体力学研究进展[J]. 高校化学工程学报, 2015, 29(4): 765-779. LI X, LI Z Q, GUAN X P, et al. Progress in hydrodynamics of gas-liquid bubble columns[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(4): 765-779. |
| [8] |
周强, 郭晓峰, 李军, 等. 竖直上升气液泡状流数学模型封闭的研究[J]. 化工进展, 2016, 35(10): 3049-3056. ZHOU Q, GUO X F, LI J, et al. Comparative investigation on closure models for the simulation of vertical gas-liquid bubbly upflow[J]. Chemical Industry and Engineering Progress, 2016, 35(10): 3049-3056. |
| [9] |
MULLER R L, PRINCE R G H. Regimes of bubbling and jetting from submerged orifices[J]. Chemical Engineering Journal, 1972, 27(8): 1583-1592. DOI:10.1016/0009-2509(72)80051-4 |
| [10] |
ALADJEM C T, SHEMER L, BARNEA D. On the interaction between two consecutive elongated bubbles in a vertical pipe[J]. International Journal of Multiphase Flow, 2000, 26(12): 1905-1923. DOI:10.1016/S0301-9322(00)00004-5 |
| [11] |
LIAO Y X, ROLAND R, LUCAS D. Baseline closure model for dispersed bubbly flow: Bubble coalescence and breakup[J]. Chemical Engineering Science, 2015, 122: 336-349. DOI:10.1016/j.ces.2014.09.042 |
| [12] |
ZUZANA B, THODORIS K, MARGARITIS K. Bubble–particle collision interaction in flotation systems[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2015, 473: 95-103. |
| [13] |
丁玉栋, 廖强, 朱恂, 等. 液体通流矩形槽道可渗透壁面处气泡生长及液相侵渗传输特性研究[J]. 机械工程学报, 2013, 49(14): 19-124. DING Y D, LIAO Q, ZHU X, et al. Characteristics of bubble growth and water invasion at the permeable sidewall in rectangular liquid flow channel[J]. Journal of Mechanical Engineering, 2013, 49(14): 19-124. |
| [14] |
杨辉, 朱春英, 马友光, 等. 非牛顿流体中双喷嘴连续气泡的生成与聚并[J]. 化学工程, 2016, 44(8): 37-41. YANG H, ZHU C Y, MA Y G, et al. Continuous formation and coalescence of bubbles through double-nozzle in non-Newtonian fluid[J]. Chemical Engineering, 2016, 44(8): 37-41. DOI:10.3969/j.issn.1005-9954.2016.08.008 |
| [15] |
杜煜昊, 熊凯文, 张莹, 等. 水平布置等径气泡上升运动数值模拟分析[J]. 计算力学学报, 2016, 33(6): 889-894. DU Y H, XIONG K W, ZHANG Y, et al. Analysis of numerical simulation on horizontal arrangement equal bubbles rising[J]. Chinese Journal of Computational Mechanics, 2016, 33(6): 889-894. |
| [16] |
GADDIS E S, VOGELPOHL A. Bubble formation in quiescent liquids under constant flow conditions[J]. Chemical Engineering Science, 1986, 41(1): 97-105. DOI:10.1016/0009-2509(86)85202-2 |




