1 前言
棕榈酸异丙酯为重要的精细化工产品之一,常用于日用洗护产品,也可作为生物柴油的组分或添加剂改善生物柴油性能,如增强其润滑性,改善其凝点、冷滤点等低温流动性能[1, 2]。目前,其合成方法多以磺酸型离子交换树脂催化丙烯与棕榈酸反应[3]或固体超强酸、负载型酸催化剂催化棕榈酸与异丙醇反应[4~7]为主,其生产工艺复杂、产品收率低、经济成本高;本实验室提出了“两步法”合成脂肪酸酯的工艺路线[8],该工艺为液相体系,无催化剂、无副反应、转化率较高且酰氯化反应尾气易回收加工为附加产品,因此,本文对以棕榈酸、异丙醇、氯化亚砜为原料,对“两步法”合成棕榈酸异丙酯的工艺过程进行热力学分析。
2 反应体系各组分热力学数据估算
“两步法”合成棕榈酸异丙酯需经酰氯化与醇解两步反应[8],即C16H32O2首先与SOCl2进行酰氯化生成C16H31ClO,而后酰氯再与(CH3)2CHOH进行醇解反应得到C19H38O2,其反应式如下:
|
$
\begin{array}{*{20}{l}}
{{\rm{C}}{{\rm{H}}_{\rm{3}}}{{\left( {{\rm{C}}{{\rm{H}}_{\rm{2}}}} \right)}_{\rm{7}}}{\rm{CH = CH}}{{\left( {{\rm{C}}{{\rm{H}}_{\rm{2}}}} \right)}_{\rm{7}}}{\rm{COOH + SOC}}{{\rm{l}}_{\rm{2}}} \to {\rm{C}}{{\rm{H}}_{\rm{3}}}{{\left( {{\rm{C}}{{\rm{H}}_{\rm{2}}}} \right)}_{\rm{7}}}{\rm{CH = }}{{\left( {{\rm{C}}{{\rm{H}}_{\rm{2}}}} \right)}_{\rm{7}}}{\rm{COCl + S}}{{\rm{O}}_{\rm{2}}}{\rm{ + HCl}}}\\
{{\rm{C}}{{\rm{H}}_{\rm{3}}}{{\left( {{\rm{C}}{{\rm{H}}_{\rm{2}}}} \right)}_{\rm{7}}}{\rm{CH = }}{{\left( {{\rm{C}}{{\rm{H}}_{\rm{2}}}} \right)}_{\rm{7}}}{\rm{COCl + }}{{\left( {{\rm{C}}{{\rm{H}}_{\rm{3}}}} \right)}_{\rm{2}}}{\rm{CHOH}} \to {\rm{C}}{{\rm{H}}_{\rm{3}}}{{\left( {{\rm{C}}{{\rm{H}}_{\rm{2}}}} \right)}_{\rm{7}}}{\rm{CH = }}{{\left( {{\rm{C}}{{\rm{H}}_{\rm{2}}}} \right)}_{\rm{7}}}{\rm{COOCH}}{{\left( {{\rm{C}}{{\rm{H}}_{\rm{3}}}} \right)}_{\rm{2}}}{\rm{ + HCl}}}
\end{array}
$
|
该体系涉及各组分的298.15 K下相关基础热力学数据除(CH3)2CHOH、SOCl2、SO2和HCl可由化工数据手册中查取(见表 1)。C16H32O2、C16H31ClO与C19H38O2的热力学数据需通过估算法计算求得。
表 1(Tab. 1)
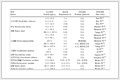
表 1 组分基础热力学数据[9]
Table 1 The thermophysical properties of several substances under standard conditions
| Component |
Smθ(298.15 K)/J·K-1·mol-1 |
ΔHfθ(298.15 K)/kJ·mol-1 |
Cp, mθ(298.15K)/J·Kw-1·mol-1 |
| (CH3)
2CHOH(l) |
180.580 |
-317.8 |
154.400 |
| SO2(g) |
248.221 |
-296.813 |
39.900 |
| SOCl2(l) |
201.73 |
-244.088 |
66.575 |
| HCl(g) |
186.896 |
-92.312 |
29.130 |
|
表 1 组分基础热力学数据[9]
Table 1 The thermophysical properties of several substances under standard conditions |
2.1 各组分相标准摩尔生成焓${\Delta _{\rm{f}}}{\rm{H}}_{\rm{m}}^{\rm{\mathtt{\mathtt{θ}} }}({\rm{g}},298.15{\rm{K}})$和熵值$S_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{g}},298.15{\rm{K}})$估算
2.1.1 各组分气相标准摩尔生成焓${\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{g}},{\rm{298}}.{\rm{15K}})$和熵值$S_{\rm{m}}^{\rm{\mathtt{θ} }}{\rm{(g,298}}{\rm{.15K)}}$估算
对该体系中C16H32O2、C16H31ClO、C19H38O2三种组分${\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{g, 298}}{\rm{.15 K}})$和$S_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{g, 298}}{\rm{.15 K}})$的估算分别采用Joback基团贡献法[10, 11]和Yoneda基团贡献法[12],各计算公式分别为式(1)、式(2):
|
$
{\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{g}},{\rm{298}}.{\rm{15K}}) = 68.29 + \sum {{n_i}\Delta {H_i}}
$
|
(1) |
|
$
S_{\rm{m}}^\mathtt{θ} ({\rm{g}},{\rm{298}}.{\rm{15K}}) = \sum {{n_i}\Delta S}
$
|
(2) |
式(1)中,ni为分子中i基团的数目,ΔHi为基团i的基团贡献值;式(2)中,ni为i基团需要取代的次数,ΔS为每一次取代的基团贡献值。通过计算,三组分的${\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{g, 298}}{\rm{.15 K}})$及$S_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{g, 298}}{\rm{.15 K}})$值见表 2。
表 2(Tab. 2)

表 2 三组分相关参数估算结果
Table 2 Relevant parameters of the main components
| Component |
T
b/K |
T
c/K |
T
r
|
ΔvHmθ(298.15 K)
/kJ·mol -1 |
ΔfHmθ(298.15 K)
/kJ·mol -1 |
Smθ(298.15 K)
/J·mol -1·K-1 |
| C16H32O2 |
624 |
778.78 |
0.3828 |
105.05 |
-145.92 |
868.02 |
| C16H31ClO |
472 |
595.44 |
0.5007 |
92.19 |
76.03 |
833.02 |
| C19H38O2 |
433 |
538.25 |
0.5539 |
114.75 |
-180.13 |
1010.88 |
|
表 2 三组分相关参数估算结果
Table 2 Relevant parameters of the main components |
2.1.2 标准摩尔蒸发焓${\Delta _v}H_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{298}}{\rm{.15 K}})$估算
因实际反应条件下上述三组分为液相,故需借助各组分${\Delta _{\rm{v}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{298}}{\rm{.15 K}})$将气相热力学数据换算为液相热力学数据。通过Tu等人[13]提出的基团贡献法进行$\Delta vH_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{298}}{\rm{.15 K}})$估算,计算式为式(3):
|
$
{\Delta _{\rm{v}}}H_m^{\rm{\mathtt{θ} }}\left( {298.15{\rm{K}}} \right) = \sum\limits_{i = 1}^m {{n_i}\left[ {{a_i}{{\left( {1 - {T\rm{_r}}} \right)}^{1/3}} + {b_i}{{\left( {1 - {T\rm{_r}}} \right)}^{2/3}} + {c_i}\left( {1 - {T\rm{_r}}} \right)} \right]}
$
|
(3) |
式(3)中,m为分子中的基团种类数;ni为分子中i基团的数目;ai,bi,ci为基团i的基团贡献值;Tr为对比温度,临界温度Tc可通过采用Joback法[14]借助组分的沸点Tb得到,计算式为式(4):
|
$
{T_{\rm{c}}} = {T_{\rm{b}}}{[0.584 + 0.965\sum {{n_i}\Delta {T_i} - {{(\sum {{n_i}\Delta {T_i}} )}^2}} ]^{ - 1}}
$
|
(4) |
式(4)中,ni为分子中i基团的数目;Ti为基团i的基团贡献值,各组分${\Delta _{\rm{v}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{298}}{\rm{.15 K}})$的估算结果见表 2。
2.1.3 标准摩尔生成焓${\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{298}}{\rm{.15 K}})$和熵值$S_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{298}}{\rm{.15 K}})$的估算
由估算得到的相关数据,依据式(5)、式(6)可求得相应组分${\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}(L, {\kern 1pt} {\kern 1pt} {\rm{298}}{\rm{.15 K}})$和$S_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{298}}{\rm{.15 K}})$。
|
$
{\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (L, {\kern 1pt} {{\kern 1pt} _{}}{\rm{298}}{\rm{.15 K}}) = {\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (g, {\kern 1pt} {{\kern 1pt} _{}}{\rm{298}}{\rm{.15 K}})-\Delta vH\rm{_m}^\mathtt{θ} ({\rm{298}}{\rm{.15 K}})
$
|
(5) |
|
$
S\rm{_m}^\mathtt{θ} (\rm{L}, {\kern 1pt} {{\kern 1pt} _{}}{\rm{298}}{\rm{.15 K}}) = S\rm{_m}^\mathtt{θ} ({\rm{g, 298}}{\rm{.15 K}})-\frac{{{\Delta _v}H\rm{_m}^\mathtt{θ} ({\rm{298}}{\rm{.15 K}})}}{{298.15{\rm{K}}}}
$
|
(6) |
经计算,该反应体系中各组分对应相态的${\Delta _v}H\rm{_m}^\mathtt{θ} ({\rm{298}}{\rm{.15 K}})$和$S_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{298}}{\rm{.15 K}})$见表 3。
表 3(Tab. 3)

表 3 各组分相应相态下的${\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (298.15 K)$和$S\rm{_m}^\mathtt{θ} (298.15{\rm{ }}K)$
Table 3 ${\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (298.15 K)$and $S\rm{_m}^\mathtt{θ} (298.15{\rm{ }}K)$of components in the reaction system
| Component |
C16H32O2(l) |
C16H31ClO(l) |
C19H38O2(l) |
SOCl2(L) |
SO2(g) |
HCl(g) |
CH(CH3)
2OH(L) |
|
ΔfHmθ(298.15 K)/kJ·mol -1 |
-250.97 |
-16.16 |
-294.88 |
-244.088 |
-296.813 |
-92.312 |
-317.86 |
|
Smθ(298.15 K)/J·mol -1·K -1 |
515.68 |
523.81 |
626.01 |
201.730 |
248.221 |
186.896 |
180.58 |
|
表 3 各组分相应相态下的${\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (298.15 K)$和$S\rm{_m}^\mathtt{θ} (298.15{\rm{ }}K)$
Table 3 ${\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (298.15 K)$and $S\rm{_m}^\mathtt{θ} (298.15{\rm{ }}K)$of components in the reaction system |
2.2 各组分摩尔热摩尔$C\rm{_{P, m}}^\mathtt{θ} (T)$的估算
Rùzicka-Domalski基团贡献法[11]估算$C_{{\rm{l, p, m}}}^\mathtt{θ} (T)$具有局限性,如C-(2H,C,=C)基团参考值仅在90~355 K可采用,同时,该法不适合用于估算酰氯化合物$C_{{\rm{l, p, m}}}^\mathtt{θ} (T)$因此,分两步估算上述三组分的$C_{{\rm{l, p, m}}}^\mathtt{θ} (T)$。
2.2.1 理想气体摩尔热容$C_{{\rm{l, p, m}}}^\mathtt{θ} (T)$估算
该反应在常压下进行,采用Joback法[11]来估算$C\rm{_{g, p, m}}^\mathtt{θ} (T)$的关联方程为式(7):
|
$
\begin{array}{l}
C\rm{_{g, p, m}}^\mathtt{θ} = \left\{ {} \right.\sum\limits_{^k} {{{\rm{N}}_k}\left( {{C\rm{_{pAk}}}} \right)}-37.93\left. {} \right\} + \left\{ {} \right.\sum\limits_{^k} {{{\rm{N}}_k}\left( {{C\rm{_{pBk}}}} \right)} + 0.210\left. {} \right\}T\\
{\begin{array}{*{20}{c}}
{}&{}&{}
\end{array}^{_{}}}_{} + \left\{ {} \right.\sum\limits_{^k} {{{\rm{N}}_k}\left( {{C\rm{_{pCk}}}} \right)}-3.91 \times {10^{-4}}){T^2} + \left\{ {} \right.\sum\limits_{^k} {{{\rm{N}}_k}\left( {{C\rm{_{pDk}}}} \right)} {\kern 1pt} {\rm{ + }}0.206 \times {10^{ - 7}}\left. {} \right\}{T^3}
\end{array}
$
|
(7) |
式(7)中,N为分子中k型基团的数目;CpAk、CpBk、CpCk、CpDk分别为为基团k的贡献值,将各组分$C\rm{_{g, p, m}}^\mathtt{θ} $与温度关系统一表达如式(8)所示。
|
$
C\rm{_{g, p, m}}^\mathtt{θ} (T) = {\rm{{\rm{A'}}}} + {\rm{B'}}T + C'{T^2} + D'{T^3}
$
|
(8) |
2.2.2 液相摩尔热容$C_{{\rm{l, p, m}}}^{\rm{\mathtt{θ} }}{\rm{(}}T{\rm{)}}$的估算
因反应体系为液相,在此采用通用性较好的Tyagi方程[10],估算相应组分的$C\rm{_{1,p,m}}^\mathtt{θ} \left( \mathit{T} \right)$如式(9):
|
$
\begin{array}{l}
C\rm{_{l, p, m}}^\mathtt{θ} (\mathit{T}){\rm{ = }}\mathit{C}_{{\rm{g, p, m}}}^\mathtt{θ} (\mathit{T}) + \mathit{R}[(-6.90287-11.2737{\mathit{T}\rm{_r}}^2 + 14.04816{\mathit{T}\rm{_r}}^6)\\
{\begin{array}{*{20}{c}}
{}&{}&{}
\end{array}_{}} + {{\mathop{\rm P}\nolimits} \rm{_r}}(0.2865-1.1364{\mathit{T}\rm{_r}}^2 + 0.031008{\mathit{T}\rm{_r}}^3{{\mathop{\rm P}\nolimits} \rm{_r}}) + \omega (17.403{\mathit{T}\rm{_r}} - 0.02706{\mathit{T}\rm{_r}}^3{{\mathop{\rm P}\nolimits} \rm{_r}})]
\end{array}
$
|
(9) |
式(9)中,Tc采用式(4)计算,Pc采用Joback法,采用Chen等提出的ω[10]的计算,如式(10)~(12),结果见表 4。
表 4(Tab. 4)

表 4 各组分相应状态下的热容及相关参数
Table 4 Heat capacities and relevant parameters of each component in the reaction system
| Component |
Relevant parameters |
Cp, mθ(T)/ J·mol -1·K -1 |
|
T
c/ K |
P
c/ bar |
P
r
|
T
br
|
ω |
A
|
B
|
C×10 4 |
D×10 7 |
E×10 15 |
| HCl(g) |
/ |
/ |
/ |
/ |
/ |
28.170 |
0.00181 |
0.01547 |
/ |
/ |
| SOCl2(l) |
556.57 |
68.76 |
0.01477 |
0.6273 |
0.31 |
-2.2653 |
0.11199 |
-2.671 |
4.50594 |
3.9293 |
| SO2(g) |
/ |
/ |
/ |
/ |
/ |
-4.690 |
0.244 |
-3.254 |
1.428 |
/ |
| CH(CH3)
2OH(l) |
519.76 |
54.23 |
0.01868 |
0.6845 |
0.603 |
-53.576 |
0.4969 |
-5.206 |
33.78 |
5.924 |
| C16H32O2(l) |
778.78 |
14.08 |
0.07196 |
0.8013 |
1.036 |
-64.275 |
1.7725 |
-10.748 |
2.0717 |
0.52353 |
| C16H31ClO(l) |
595.44 |
13.44 |
0.07539 |
0.7927 |
0.89 |
-48.6169 |
1.7192 |
-11.147 |
1.7914 |
2.6206 |
| C19H38O2(l) |
538.25 |
10.9 |
0.09296 |
0.8045 |
0.878 |
-47.8251 |
1.933 |
-12.449 |
1.572 |
4.8032 |
|
表 4 各组分相应状态下的热容及相关参数
Table 4 Heat capacities and relevant parameters of each component in the reaction system |
|
$
{P_{\rm{c}}} = {(0.113 + 0.0032{n_{\rm{A}}} - \sum {\Delta {P_i}} )^{ - 2}}
$
|
(10) |
|
$
\omega = \frac{{0.3(0.2803 + 0.4789{T_{{\rm{br}}}})}}{{(1 - {T_{{\rm{br}}}})(0.9803 - 0.5211{T_{{\rm{br}}}})}}\log {P_{\rm{c}}} - 1
$
|
(11) |
|
$
{{\rm{T}}_{{\rm{br}}}}{\rm{ = }}{{\rm{T}}_{\rm{b}}}{\rm{/}}{{\rm{T}}_{\rm{c}}}
$
|
(12) |
将式(10)、(11)及(12代入式(9),可得到各组分液相摩尔热容$C_{{\rm{l, p, m}}}^\mathtt{θ} (T)$与温度的对应关系。
2.2.3 相应状态下摩尔热容$C_{{\rm{p, m}}}^\mathtt{θ} (T)$的计算式
整个反应体系中各组分对应相态下$C_{{\rm{p, m}}}^\mathtt{θ} (T)$的统一表达为式(13)且各自对应参数值如表 4所示:
|
$
C\rm{_{p, m}}^\mathtt{θ} (\mathit{T}) = \mathit{A} + \mathit{BT} + \mathit{C}{\mathit{T}^2} + \mathit{D}{\mathit{T}^3} + \mathit{E}{\mathit{T}^6}
$
|
(13) |
2.3 任意温度下各组分标准摩尔生成焓${\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (\mathit{T})$及熵值$S\rm{_m}^\mathtt{θ} (\mathit{T})$的估算
任意温度下的标准摩尔生成焓${\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$及熵值$S_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$计算式分别为:
|
$
{\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (\mathit{T}) = {\Delta \rm{_f}}\mathit{H}\rm{_m}^\mathtt{θ} ({298.15_{}}K) + \int_{{\rm{298}}{\rm{.1}}{{\rm{5}}_{}}{\rm{K}}}^\mathit{T} {C\rm{_{P, m}}^\mathtt{θ} (\mathit{T})} d\mathit{T}
$
|
(14) |
|
$
S_{\rm{m}}^{\rm{ \mathtt{θ} }}(T) = S_{\rm{m}}^{\rm{ \mathtt{θ} }}({\rm{298}}{\rm{.15 K}}) + \int_{{\rm{298}}{\rm{.15 K}}}^T {\frac{{C_{{\rm{p,m}}}^{\rm{ \mathtt{θ} }}(T)}}{T}{\rm{d}}T}
$
|
(15) |
将式(13)分别代入式(14)、式(15),积分整理后得到${\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$及$S_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$表达式为:
|
$
{\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{ \mathtt{θ} }}(T) = aT + b{T^2} + c{T^3} + d{T^4} + e{T^7} + f
$
|
(16) |
|
$
S_{\rm{m}}^{\rm{ \mathtt{θ} }}(T) = a`{\rm{lnT}} + b`T + c`{T^2} + d`{T^3} + e`{T^6} + f`
$
|
(17) |
根据上述各组分${\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}({298.15_{}}{\rm{K}})$、$S_{\rm{m}}^{\rm{\mathtt{θ} }}({\rm{298}}{\rm{.15 K}})$和$C_{{\rm{p,m}}}^\mathtt{θ} $数据,通过式(16)和(17)即可得到各组分相应相态下的标准摩尔生成焓${\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$和熵值$S_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$系数值,见表 5。
表 5(Tab. 5)

表 5 各组分相应状态的${\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (\mathit{T})$和$S\rm{_m}^\mathtt{θ} (\mathit{T})$
Table 5 ${\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (\mathit{T})$and $S\rm{_m}^\mathtt{θ} (\mathit{T})$of each component in the reaction system
| Component |
ΔfHmθ(T)/ J·mol -1 |
Smθ(T)/ J·mol -1·K -1 |
|
a
|
b
|
c×10 4 |
d×10 7 |
e×10 15 |
f
|
a
,
|
b
,
|
c
,×10 4 |
d
,×10 7 |
e
,×10 15 |
f
,
|
| HCl(g) |
28.17 |
0.001 |
0.005 |
0 |
0 |
-100805 |
28.17 |
0.002 |
0.008 |
0 |
0 |
25.79 |
| SOCl2(l) |
-2.26 |
0.056 |
-0.890 |
1.126 |
0.561 |
-247038 |
-2.26 |
0.112 |
-1.334 |
1.501 |
0.655 |
188.68 |
| SO2(g) |
-4.69 |
0.122 |
-1.085 |
0.357 |
0 |
-303667 |
-4.69 |
0.244 |
-1.627 |
0.476 |
0 |
215.39 |
| CH(CH3)
2OH(l) |
-53.58 |
0.248 |
-1.735 |
8.445 |
0.846 |
-326223 |
-53.58 |
0.497 |
-2.603 |
11.26 |
0.987 |
330.28 |
| C16H32O2(l) |
-64.28 |
0.886 |
-3.583 |
0.518 |
0.075 |
-301517 |
-64.28 |
1.772 |
-5.374 |
0.691 |
0.087 |
399.30 |
| C16H31ClO(l) |
-48.62 |
0.860 |
-3.716 |
0.448 |
0.374 |
-68662 |
-48.62 |
1.719 |
-5.574 |
0.597 |
0.437 |
335.89 |
| C19H38O2(l) |
-47.83 |
0.966 |
-4.150 |
0.393 |
0.686 |
-355992 |
-47.82 |
1.933 |
-6.224 |
0.524 |
0.801 |
375.55 |
|
表 5 各组分相应状态的${\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (\mathit{T})$和$S\rm{_m}^\mathtt{θ} (\mathit{T})$
Table 5 ${\Delta \rm{_f}}H\rm{_m}^\mathtt{θ} (\mathit{T})$and $S\rm{_m}^\mathtt{θ} (\mathit{T})$of each component in the reaction system |
3 定压比热容的测定
该反应体系中,C16H32O2、C16H31ClO、C19H38O2的热力学性质无法从文献获取,为验证估算方法的可靠性,借助仪器对可测参数进行测定。在此采用差示扫描量热仪DSC-60进行比热容测定。测定过程中,选用α-Al2O3作为参比物质,验证仪器可靠[15, 16]。在此基础上,进一步测定C16H32O2、C19H38O2的热容,将测得的结果Cp, exp同估算值Cp, est进行对比,见表 6,结果表明两种方法得到数值误差均不超5%,误差在可接受范围,采用估算法进行热容计算可行。
表 6(Tab. 6)

表 6 C16H32O2、C19H38O2比热容估算值与实验值对比
Table 6 Experimental and estimate values of the specific heat for C16H32O2 and C19H38O2
| T/K |
C16H32O2 |
C19H38O2 |
|
C
p, est
/ J×g -1×K -1 |
C
p, exp/ J×g -1×K -1 |
Relative error/% |
C
p, est/ J×g -1×K -1 |
C
p, exp/ J×g -1×K -1 |
Relative error/% |
| 340 |
1.6471 |
1.5958 |
3.2148 |
1.3866 |
1.3804 |
-0.4460 |
| 350 |
1.6903 |
1.6713 |
1.1353 |
1.4202 |
1.4131 |
-0.4999 |
| 360 |
1.7327 |
1.7079 |
1.4546 |
1.4532 |
1.4677 |
0.9890 |
| 370 |
1.7746 |
1.7236 |
2.9583 |
1.4856 |
1.5194 |
2.2234 |
| 380 |
1.8158 |
1.7997 |
0.8930 |
1.5175 |
1.5574 |
2.5605 |
|
表 6 C16H32O2、C19H38O2比热容估算值与实验值对比
Table 6 Experimental and estimate values of the specific heat for C16H32O2 and C19H38O2 |
4 棕榈酸异丙酯合成反应的热力学分析
4.1 两步反应的${\Delta \rm{_r}}H\rm{_m}^\mathtt{θ} (\mathit{T})$、${\Delta \rm{_r}}S\rm{_m}^\mathtt{θ} (\mathit{T})$、${\Delta \rm{_r}}G\rm{_m}^\mathtt{θ} (\mathit{T})$、$ K_{}^\mathtt{θ} (T)$计算
根据上述各组分热力学数据的计算结果,两步反应的热力学性质${\Delta _{\rm{r}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$、${\Delta _{\rm{r}}}S_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$、${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$及$K_{}^{\rm{\mathtt{θ} }}(T)$可由式(18)~(22)分别计算:
|
$
{\Delta _{\rm{r}}}H_{\rm{m}}^{\rm{ \mathtt{θ} }}(T) = \sum\limits_{^B} {{v_B}} {\Delta _{\rm{f}}}H_{\rm{m}}^{\rm{ \mathtt{θ} }}(T)
$
|
(18) |
|
$
{\Delta _{\rm{r}}}S_{\rm{m}}^{\rm{ \mathtt{θ} }}(T) = \sum\limits_{^B} {{\nu _B}S_m^ \mathtt{θ} (T)}
$
|
(19) |
|
$
{\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{ \mathtt{θ} }}(T) = {\Delta _{\rm{r}}}H_{\rm{m}}^{\rm{ \mathtt{θ} }}(T) - T{\Delta _r}S_{\rm{m}}^{\rm{ \mathtt{θ} }}(T)
$
|
(20) |
|
$
{\Delta _r}G_{\rm{m}}^{\rm{ \mathtt{θ} }}(T) = - RT\ln K_{}^{\rm{ \mathtt{θ} }}(T)
$
|
(21) |
|
$
{K^ \mathtt{θ} }(T) = {\rm{exp}}(\frac{{ - {\Delta _r}G_{\rm{m}}^{\rm{ \mathtt{θ} }}(T)}}{{RT}})
$
|
(22) |
根据反应体系的物料性质,${\Delta _{\rm{r}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$、$ {\Delta _{\rm{r}}}S_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$、${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(T)$及$K_{}^{\rm{\mathtt{θ} }}(T)$,分别选取343.15、348.15、353.15、358.15、363.15、368.15 K为反应温度,计算出各步反应的并附基准温度298.15 K下相应数据,其结果见表 7。
表 7(Tab. 7)

表 7 棕榈酸异丙酯合成反应的热力学性质
Table 7 Thermophysical properties of the isopropyl palmitate synthesis
| Reaction temperature |
Acylation reaction |
Alcoholysis reaction |
|
T/K |
ΔrHmθ(1)
/kJ·mol -1 |
ΔrSmθ(1)
/kJ·mol -1·K -1 |
ΔrGmθ(1)
/kJ·mol -1 |
Kθ(T)(1)
|
ΔrHmθ(2)
/kJ·mol -1 |
ΔrSmθ(2)
/kJ·mol -1·K -1 |
ΔrGmθ(2)
/kJ·mol -1 |
Kθ(T)(2)
|
| 298.15 |
89.537 |
240.725 |
18.969 |
4.167×10 -4 |
-52.888 |
109.477 |
-84.981 |
1.389×10 15 |
| 343.15 |
91.757 |
247.727 |
6.749 |
9.388×10 -2 |
-56.956 |
96.782 |
-90.167 |
5.319×10 13 |
| 348.15 |
91.960 |
248.314 |
5.547 |
1.470×10 -1 |
-57.530 |
95.121 |
-90.632 |
4.020×10 13 |
| 353.15 |
92.160 |
248.883 |
4.267 |
2.338×10 -1 |
-58.137 |
93.390 |
-91.117 |
3.004×10 13 |
| 358.15 |
92.355 |
249.431 |
3.058 |
3.579×10 -1 |
-58.779 |
91.583 |
-91.565 |
2.294×10 13 |
| 363.15 |
92.545 |
249.959 |
1.810 |
5.490×10 -1 |
-57.895 |
89.703 |
-92.019 |
1.745×10 13 |
| 368.15 |
92.730 |
250.466 |
0.559 |
8.331×10 -1 |
-60.173 |
87.746 |
-92.463 |
1.333×10 13 |
|
表 7 棕榈酸异丙酯合成反应的热力学性质
Table 7 Thermophysical properties of the isopropyl palmitate synthesis |
4.2 合成反应的热力学性质分析
4.2.1 对热力学函数${\Delta _{\rm{r}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}$、${\Delta _{\rm{r}}}S_{\rm{m}}^{\rm{\mathtt{θ} }}$、${\Delta _{\rm{r}}}G$的分析
由表 7可看出,在上述温度范围内,酰氯化反应的${\Delta _{\rm{r}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}(1)$、${\Delta _{\rm{r}}}S_{\rm{m}}^{\rm{\mathtt{θ} }}(1)$、${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(1)$均为正值,但${\Delta _{\rm{r}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}(1)$${\Delta _{\rm{r}}}S_{\rm{m}}^{\rm{\mathtt{θ} }}(1)$和随温度升高而增大,而${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(1)$呈减小趋势,表明酰氯化为吸热反应,且在选取条件下不可自发进行,随着反应温度升高,反应体系吸热量及无序程度增大,可自发进行的趋势变大;醇解反应的${\Delta _{\rm{r}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}(2)$、均为负值,${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(2)$为正值,${\Delta _{\rm{r}}}S_{\rm{m}}^{\rm{\mathtt{θ} }}(2)$和${\Delta _{\rm{r}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}(2)$数值随温度升高而减小,${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(2)$数值呈增大趋势,表明醇解为放热反应,且在选取条件下可自发进行,随着反应温度升高,反应体系放热量及无序程度降低。
${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}$关系到平衡常数的大小即反应所能达到的最高限度,热力学中有一条近似规则[17]:当${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}$在0~41.84 kJ·mol-1时,化学反应并不是一定不能进行,可以通过改变外部条件使反应朝着有利于生成产物的方向进行。对于酰氯化反应,虽然${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(1)$为正值,但其数值较小,且反应体系中反应主体为液相,副产物SO2、HCl气体的连续排出有助于该步反应的进行;另外,该反应体系中酰氯化产物棕榈酸酰氯为醇解反应的反应物,两步反应是耦合的[17],且醇解反应${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(2)$的强负值可抵消${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(1)$而有余,使得整个反应的吉布斯自由能变${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}$为负值,即整体反应是可自发进行的,在此可理解为醇解的${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(2)$强负值带动了酰氯化反应的顺利发生。
4.2.2 对平衡常数Kθ(T)的分析
平衡常数Kθ(T)是化学反应可逆性的定量表征,Kθ(T)数值越大则反应越完全。一般认为K < 10-5反应很难进行,等同为不反应;K > 105反应较为完全,即可看作不可逆反应;同时,当平衡条件作出改变时,会引起化学平衡移动,化学平衡移动满足勒夏特列原理。由表 7可看出,Kθ(T)随着温度的升高而增大但数值较小,表明增加反应温度对棕榈酸酰氯的生成有利,但反应程度受限;Kθ(T)随着温度的升高而减小但数值较大,降低反应温度对醇解反应的正向进行有利,且该步反应较为完全。但在整体反应过程中,由于酰氯化反应主产物参与醇解反应被及时消耗,且两步反应副产的气体又被连续及时地移出反应系统,从而造成化学平衡移动,有助于两步反应正向进行,保证棕榈酸异丙酯合成反应的顺利进行。
5 棕榈酸异丙酯的合成
为考察反应是否可正常进行,分别选取338.15 K、343.15 K,β=n(氯化亚砜):n(棕榈酸)=1.3、β=n(异丙醇):n(棕榈酸酰氯)=1.3,得到对应温度下反应时间与棕榈酸转化率的关系,结果见表 8,各步反应的转化率较高,表明该反应可正常进行。
表 8(Tab. 8)

表 8 不同反应温度下反应的取样分析结果
Table 8 Related results under different temperatures
Reaction
temperature
/K |
Reaction time/min |
Reaction time/min |
| 20 |
40 |
60 |
80 |
100 |
20 |
40 |
60 |
80 |
100 |
| Conversion rate of palmitic acid/% |
Conversion rate of isopropl palmitate/% |
| 338.15 |
0.7798 |
0.9203 |
0.9652 |
0.9825 |
0.9924 |
0.8031 |
0.9298 |
0.9697 |
0.9866 |
0.9929 |
| 343.15 |
0.8467 |
0.9487 |
0.9798 |
0.9926 |
0.9971 |
0.8596 |
0.9542 |
0.9858 |
0.9953 |
0.9982 |
|
表 8 不同反应温度下反应的取样分析结果
Table 8 Related results under different temperatures |
6 结论
(1) 针对“两步法”合成棕榈酸异丙酯的工艺路线,采用Joback与Yoneda基团贡献法及Tyagi方程对反应体系中相关物质所缺乏的热力学数据进行估算,并结合有关文献数据,计算得到了该合成工艺各步反应的${\Delta _{\rm{r}}}H_{\rm{m}}^{\rm{\mathtt{θ} }}$、${\Delta _{\rm{r}}}S_{\rm{m}}^{\rm{\mathtt{θ} }}$、${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}$及$K_{}^{\rm{\mathtt{θ} }}$。结果表明酰氯化为吸热反应,且单独存在时较难进行;醇解为放热反应,且反应可进行完全。
(2) 酰氯化和醇解两步反应为耦合反应,尾气的排出与吸收等均有助于酰氯化反应的进行;醇解反应的${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(2)$负值绝对值远大于酰氯化${\Delta _{\rm{r}}}G_{\rm{m}}^{\rm{\mathtt{θ} }}(1)$的绝对值,可促使棕榈酸异丙酯合成反应的顺利进行。
(3) 估算得到的有关热力学数据,为棕榈酸异丙酯合成工艺的开发、工程设计以及规模生产等提供了热力学数据。




