比定压热容作为流体基本热力学性质之一,在流体能量关系式和高精度状态方程构建中具有难以替代的作用。当前,对制冷剂环保特性提出越来越苛刻的要求,例如全球变暖潜能值(global warming potential,GWP)和臭氧消耗潜能值(ozone depletion potential,ODP)。开发氢氟烷烃类(Hydrofluorocarbons, HFCs)和氢氟烯烃类(Hydrofluoroolefins, HFOs)工质为主的环保制冷剂成为研究热点之一[1-3]。精确测定这类制冷工质液相比定压热容对理论分析与工业应用均有重要意义。低沸点流体液相比定压热容测量方法目前主要有3种:流动量热法、热弛豫法和准稳态量热法。LIU和TANAKA等[4-6]用改进流动量热法测定了异丁烷(isobutane,R600a)、反式-1-氯-3, 3, 3-三氟丙烯((E)-1-chloro-3, 3, 3-trifluoropropene, R1233zd(E))和1, 1, 1, 3, 3-五氟丙烷(1, 1, 1, 3, 3-perfluoropropane, R245fa)液相比定压热容。利用流动量热法测量液相比定压热容,相对不确定度在0.5%~1.5%。但是,其对循环泵稳定性有极高要求,获得一个实验数据所需时间很长。为此,TANAKA等[7-8]应用热弛豫法测量2, 3, 3, 3-四氟丙烯(2, 3, 3, 3-tetrafluoropropene, R1234yf)和反式-1, 3, 3, 3-四氟丙烯((E)-1, 3, 3, 3-tetrafluoropropene,R1234ze(E))液相比定压热容。热弛豫法操作简单,但测量过程易受热不均,其相对不确定度高达5%。理论分析与工业应用中,希望得到较多高精度比定压热容数据。流动量热法与热弛豫法有着各自的优、缺点,难以满足目前研究开发需求,亟需发展更优异的测量方法。HYKRDA等[9]采用准稳态量热法测量1, 1, 1, 2-四氟乙烷(1, 1, 1, 2-tetrafluoroethane, R134a)和1, 1, 1, 2, 3, 3, 3-七氟丙烷(1, 1, 1, 2, 3, 3, 3-heptafluoropropane,R227ea)液相比定压热容。该方法操作比较简单,在测量过程流体处于静止状态,无需使用循环泵以及测量流体质量流量,一次实验能获得多个比定压热容数据,其精度与流动量热法基本相当。GAO和HE等[10-15]基于C80量热仪开发了准稳态液相比定压热容测量装置,测量了R1234ze(E)和1, 1, 1, 2, 3, 3-六氟丙烷(1, 1, 1, 2, 2, 3-hexafluoropropane, R236fa)等液相比定压热容。研究结果也表明准稳态量热法具有综合优势,比较适合测量制冷工质等低沸点流体液相比定压热容。通过进一步分析准稳态低沸点流体液相比定压热容测量工作机理以及主要误差影响因素,发现测量过程对流现象对测量精度有较大影响,通过修正有望进一步提升比定压热容测量精度。
本文首先建立准稳态液相比定压热容测量装置数学物理修正模型;接着,基于数学物理修正模型,应用计算流体动力学(CFD)方法开展苯和水仿真计算,并与实验测量数据进行对比,从而验证数学物理修正模型准确性;最后,把数学物理修正模型和CFD方法应用于R1234ze(E)和R236fa液相比定压热容数据修正。本文的研究为获取以新型环保制冷工质为代表的低沸点流体高精度液相比定压热容数据提供新思路。
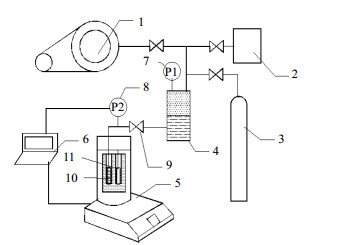
2 实验原理 2.1 实验系统本文讨论如图 1所示的基于C80量热仪准稳态液相比定压热容测量装置,量热精度为0.1%,量热分辨率为0.1 μW,温度的测量精度为0.05 K,可在环境温度至300 ℃、压力10 MPa以内用于多种低沸点流体液相比定压热容精确测量[14]。该装置主要包括压力平衡单元(真空泵、高压储液罐、气罐),测控装置和C80量热仪(包含2个池,其中一个作为测量池用于样品/参比流体测量,另一个保持空置作为参照池)以及连接管、阀等,具有操作简单、测量精度高等优点。测量时,首先用真空泵对压力平衡罐和测量池进行抽真空,关闭V1后进行制冷剂充注;等待压力稳定后,开启V1,让制冷剂通过管道流入测量池;充液完成后,将高压氦气充灌至压力平衡罐中;达到设定压力并稳定后,开始运行升温程序。
|
图 1 准稳态液相比定压热容测量装置流程图 Fig.1 Schematic diagram of the measuring device for quasi-steady state isobaric heat capacity of fluids in liquid phase 1. vacuum pump 2. refrigerant tank 3. pressurized gas cylinder 4. pressure balance container 5. C80 calorimeter 6. computer 7. P1, pressure gauge 8. P2, pressure sensor 9. valve 10. sample cell 11. contrast cell |
为了消除测量池以及参照池自身材料热容对测量精度的影响,首先需要对空白样品池/参照池进行一次相同设定的加热升温,得到空白样品池加热热流HFblank。准稳态液相比定压热容测量装置利用参比法对样本/参比流体进行测量[16],设定相同升温速率和温区,进行2次测量实验,样品池内2次实验放置对象分别是待测参比流体和样本流体,通过内置传感器得到参比流体和样本流体加热热流HFref和HFsample。根据液相比定压热容计算式得
| ${c_{{p_{{\rm{ref}}}}}} = \frac{{H{F_{{\rm{ref}}}} - H{F_{{\rm{blank}}}}}}{{{\rho _{{\rm{ref}}}}{V_{{\rm{ref}}}}{{\left( {dT/d\tau } \right)}_{{\rm{ref}}}}}}$ | (1) |
| ${c_{{p_{{\rm{sample}}}}}} = \frac{{H{F_{{\rm{sample}}}} - H{F_{{\rm{blank}}}}}}{{{\rho _{{\rm{sample}}}}{V_{{\rm{sample}}}}{{\left( {dT/d\tau } \right)}_{{\rm{sample}}}}}}$ | (2) |
式中:(dT/dτ)ref和(dT/dτ)sample分别为参比流体和样本流体测量时的温升速率,K·s-1;τ为时间,s;cpref和cpsample分别为参比流体和样本流体比定压热容,kJ·kg-1·K-1;ρref和ρsample分别为参比流体和样本流体密度,kg·m-3;Vref和Vsample分别为参比流体和样本流体测量池体积(这里取Vsample=Vref),m3。由式(1)、(2)得到样本流体液相比定压热容计算式:
| ${c_{{p_{{\rm{sample}}}}}} = {c_{{p_{{\rm{ref}}}}}} \cdot \frac{{{\rho _{{\rm{ref}}}}}}{{{\rho _{{\rm{sample}}}}}} \cdot \frac{{{V_{{\rm{ref}}}}}}{{{V_{{\rm{sample}}}}}} \cdot \frac{{H{F_{{\rm{sample}}}} - H{F_{{\rm{blank}}}}}}{{H{F_{{\rm{ref}}}} - H{F_{{\rm{blank}}}}}}$ | (3) |
若已知参比流体相关热物性,根据式(3)即可计算得到样本流体的液相比定压热容。
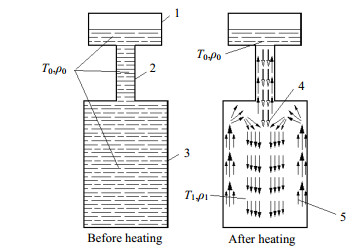
在测量开始,测量池、压力平衡罐以及连接管装有密度为ρ0,初始温度为T0的液相流体。加热后,在测量池和压力平衡罐之间形成一个非等温流场。测量池底部流体因为温度上升(T1),密度减小,从而在测量池和压力平衡罐之间发生对流现象,导致部分热流体流出测量池,并有部分冷流体(T0)流入测量池。结果测量池内被测流体的实际密度大于直接根据测量池温度得到的密度,从而可能产生比较显著的测量误差,并且随着测量池温度持续上升,对测量误差的影响会逐渐变大。测量池和压力平衡罐之间流体对流现象如图 2所示。
|
图 2 测量过程流体对流示意图 Fig.2 Schematic diagram of fluid convection during measurement 1. pressure balance container 2. connecting pipe 3. sample cell 4. cold refrigerant fluid 5. hot refrigerant fluid |
因此,需要对式(3)中,ρref和ρsample或者Vsample和Vref进行修正。通过修正体积Vsample和Vref,即通过计算测量池和连接管之间控制面的流体流速获取流体体积变化量ΔVsample和ΔVref。故而,式(3)变为
| ${c_p}_{_{{\rm{sample}}}} = {c_p}_{_{{\rm{ref}}}} \cdot \frac{{{\rho _{{\rm{ref}}}}}}{{{\rho _{{\rm{sample}}}}}} \cdot \frac{{H{F_{{\rm{sample}}}} - H{F_{{\rm{blank}}}}}}{{H{F_{{\rm{ref}}}} - H{F_{{\rm{blank}}}}}} \cdot \frac{{{V_{_{{\rm{ref}}}}} + \Delta {V_{{\rm{ref}}}}}}{{{V_{{\rm{sample}}}} + \Delta {V_{{\rm{sample}}}}}}$ | (4) |
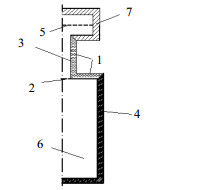
为获取测量过程流体体积变化,本文建立包括测量池、压力平衡罐及其连接管在内的CFD仿真模型,开展仿真计算、分析。几何模型示意图如图 3所示。测量池、压力平衡罐及其连接管道均为圆柱形,可在柱坐标中建立二维轴对称模型,并通过围绕对称轴旋转来得到三维结果。各边界初值及边界条件如表 1所示:对于流体区域6,采用黏性不可压缩流体的纳维-斯托克斯方程以及连续性方程描述该流动场,如式(5)、(6)所示:
|
图 3 测量池、压力平衡罐及连接管半截面模型示意图 Fig.3 Schematic diagram of the cross-section of sample cell, pressure balance container and connecting tubes 1. the outer wall surface of connecting pipe 2. the control surface of calculating ΔVsample and ΔVref 3. the inner wall surface of pressure balance tank connecting pipe surface 4. sample cell heating wall 5. pressure balance tank gas-liquid interface 6. fluid area 7. pressure balance tank wall |
|
|
表 1 初值及边界条件 Table 1 Initial values and boundary conditions |
| $\left\{ \begin{array}{l} \rho \frac{{\partial {v_r}}}{{\partial t}} + \rho ({v_r}\frac{{\partial {v_r}}}{{\partial r}} + \frac{{{v_\theta }}}{r}\frac{{\partial {v_r}}}{{\partial \theta }} + {v_z}\frac{{\partial {v_r}}}{{\partial z}} - \frac{{{v_\theta }^2}}{r}) \\ = {F_r} - \frac{{\partial p}}{{\partial r}} + \mu ({\nabla ^2}{v_r} - \frac{{{v_r}}}{{{r^2}}} - \frac{2}{{{r^2}}}\frac{{\partial {v_\theta }}}{{\partial \theta }}) - \frac{2}{3}\mu (2\frac{{\partial {u_r}}}{{\partial r}} + r\frac{{{\partial ^2}{u_r}}}{{\partial {r^2}}} + \frac{{{\partial ^2}{u_\theta }}}{{\partial \theta \partial r}} + \frac{{\partial {u_z}}}{{\partial z}} + r\frac{{{\partial ^2}{u_z}}}{{\partial z\partial r}}) \\ \rho \frac{{\partial {v_\theta }}}{{\partial t}} + \rho ({v_r}\frac{{\partial {v_\theta }}}{{\partial r}} + \frac{{{v_\theta }}}{r}\frac{{\partial {v_\theta }}}{{\partial \theta }} + {v_z}\frac{{\partial {v_\theta }}}{{\partial z}} + \frac{{{v_\theta }{v_r}}}{r}) \\ = {F_\theta } - \frac{1}{r}\frac{{\partial p}}{{\partial \theta }} + \mu ({\nabla ^2}{v_\theta } - \frac{{{v_\theta }}}{{{r^2}}} + \frac{2}{{{r^2}}}\frac{{\partial {v_r}}}{{\partial \theta }}) - \frac{2}{3}\frac{\mu }{{{r^2}}}(\frac{{\partial {u_r}}}{{\partial \theta }} + r\frac{{{\partial ^2}{u_r}}}{{\partial r\partial \theta }} + \frac{{{\partial ^2}{u_\theta }}}{{\partial {\theta ^2}}} + r\frac{{{\partial ^2}{u_z}}}{{\partial z\partial \theta }}) \\ \rho \frac{{\partial {v_\theta }}}{{\partial t}} + \rho ({v_r}\frac{{\partial {v_z}}}{{\partial r}} + \frac{{{v_\theta }}}{r}\frac{{\partial {v_z}}}{{\partial \theta }} + {v_z}\frac{{\partial {v_z}}}{{\partial z}}) \\ = {F_z} - \frac{{\partial p}}{{\partial z}} + \mu {\nabla ^2}{v_z} - \frac{2}{3}\frac{\mu }{r}(\frac{{\partial {u_r}}}{{\partial z}} + r\frac{{{\partial ^2}{u_r}}}{{\partial r\partial z}} + \frac{{{\partial ^2}{u_\theta }}}{{\partial \theta \partial z}} + r\frac{{{\partial ^2}{u_z}}}{{\partial {z^2}}}) \\ \end{array} \right.$ | (5) |
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho u} \right) = 0$ | (6) |
在旋转得到的三维柱坐标系中,u(r, θ, z)为任一点的速度,m·s-1;νr, νθ, νz为在3个坐标方向上的分速度,m·s-1;F为体积力,kg·m·s-2;μ是动力黏度,Pa·s;其中,
| ${\nabla ^2} = \frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {\theta ^2}}} + \frac{{{\partial ^2}}}{{\partial {z^2}}}$ | (7) |
在测量池加热壁面,引入表示热量在其内部传递的传热方程,如式(8):
| $\rho {c_p}\frac{{\partial T}}{{\partial \tau }} + \nabla \cdot \mathit{\boldsymbol{q}} = 0$ | (8) |
流体内部的传热方程由式(9)描述:
| $\rho {c_p}\frac{{\partial T}}{{\partial \tau }} + \rho {c_p}u \cdot \nabla T + \nabla \cdot \mathit{\boldsymbol{q}}= Q + {Q_p} + {Q_{vd}}$ | (9) |
式中:Qp和Qvd分别为压力变化做的功和黏性耗散,J;Q为流体温升吸收的热量,J;q为流体热传导的热流密度矢量,J·m-2·s-1。根据傅里叶定律q满足:
| $\mathit{\boldsymbol{q}} = - k\nabla T$ | (10) |
式中:k为导热系数,W·m-1·K-1。
如前所述,在测量过程为了消除测量池自身热容对测量误差的影响,通过扫描空白测量池和参照池的热流HFblank,并在液相比定压热容计算过程减去HFblank,具体如式(4)所示。为了在CFD仿真模型中也消除测量池自身材料对仿真结果的影响,采用多物理场仿真软件(COMSOL Multiphysics)自带材料数据库来描述指定各区域的材料参数随温度的变化关系,包括密度、比定压热容、比热率(比定压热容与比定容热容的比值)、导热系数、动力黏度[17]。在求解模型时,选取测量池与连接管的交界面作为控制面,在其上对每一个微元处的z轴方向速度进行积分并求和,得到该控制面上z方向的总体积流量。在获取了z方向的体积流量与时间的对应关系后,选取时间步长与之相乘,作为流体在某一时间步长中体积变化量
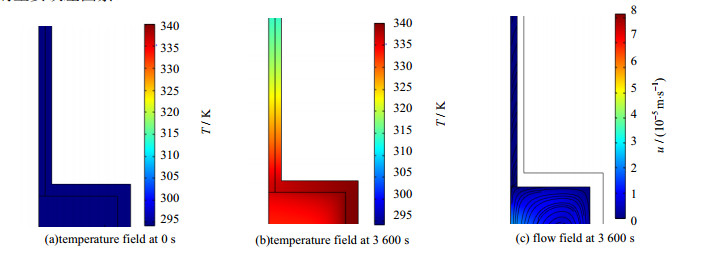
由于水和苯有高精度的液相比定压热容、密度等数据,常被选作比定压热容测量的标准参比物。为了验证通过CFD方法修正体积Vsample和Vref提高比定压热容测量精度的可行性,选择苯为样本流体,水作为参比流体开展CFD仿真模型验证。在0.1、1.1和2.0 MPa压力工况下,对苯从温度295 K加热至340.15 K进行仿真计算,设置升温速率为0.5 K·min-1。测量池和连接管在未加热以及加热3 600 s后温度场仿真结果如图 4(a)、(b)所示,流场如图 4(c)所示。对比图(a)和(b)的温度分布,可以看出在升温到335.15 K时,测量池内温差并不显著,但是测量池与压力平衡罐之间有显著的温度梯度。从图 4(c)可以进一步看出,测量池与压力平衡罐之间存在明显对流想象,初步证实了2.2小节所作猜测,对流很可能是影响测量精度的主要误差因素。
|
图 4 连接管与测量池的温度场和流场 Fig.4 Temperature and flow fields of connecting tubes and sample cells |
通过CFD修正后苯的液相比定压热容结果如表 2所示。其中,cpexp为比定压热容实验值,cpees为工程方程求解器(engineering equation solver,EES)软件计算值[17],cpmod是修正后比定压热容,RDexp(relative deviation)和RDmod分别为实验值与修正后数据以及EES计算值的偏差百分数。RDexp和RDmod的计算如式(11)、(12):
| ${{\rm{RD}}_{\exp }} = ({c_p}_{_{\exp }} - {c_p}_{_{{\rm{ees}}}})/{c_p}_{_{{\rm{ees}}}} \times 100\% $ | (11) |
| ${{\rm{RD}}_{\bmod }} = ({c_p}_{_{\bmod }} - {c_p}_{_{{\rm{ees}}}})/{c_p}_{_{{\rm{ees}}}} \times 100\% $ | (12) |
|
|
表 2 苯比定压热容修正结果 Table 2 Modified results of the isobaric heat capacity of benzene |
为了比较修正效果,分别计算修正前后的平均绝对偏差(average absolute deviation,AAD),计算方法如式(13)、(14):
| ${{\rm{AAD}}_{{\rm{exp}}}} = \left| {\sum\nolimits_{i = 1}^N {R{D_{\exp }}_{_i}} /N} \right|$ | (13) |
| ${{\rm{AAD}}_{{\rm{mod}}}} = \left| {\sum\nolimits_{i = 1}^N {R{D_{\bmod }}_{_i}} /N} \right|$ | (14) |
通过CFD修正测量池与压力平衡罐之间对流对比定压热容的影响后,各点比定压热容的RD%均有所减小,平均绝对偏差AADexp=0.49%下降至AADmod=0.44%。最大绝对偏差(maximum absolute deviation,MAD)从1.43%下降到1.38%。结果表明,所建立的准稳态流体液相比定压热容测量装置CFD仿真模型具有比较高的计算精度,能比较准确地计算出比定压热容细小变化。
计算ΔVsample和ΔVref目的是减小测量池与压力平衡罐之间对流对测量误差的影响。ΔVsample和ΔVref与样品流体及参比流体密度随温度升高而伴随的变化幅度紧密相关。测量池中苯和水的密度变化情况如表 3。从表 3中可以看出,在给0.1 MPa压力条件下,苯由293.15 K加热到340.15 K的密度变化幅度Δρ1为5.77%,水的密度变化幅度Δρ2为1.88%;在1.1和2 MPa条件下,苯密度变化幅度分别为5.69%和5.69%;水的密度变化幅度为1.88%和1.87%。在不同压力下,苯和水的密度变化幅度基本不变。故而,通过CFD修正测量池与压力平衡罐之间对流对比定压热容的影响基本相似,约为0.05%。从苯和水的仿真结果,可以初步推断随着流体密度变化增大,对流现象加剧,通过CFD方法修正会有更好效果。
|
|
表 3 苯和水密度随温度变化情况 Table 3 Density variations of benzene and water at different temperatures |
R1234ze(E)作为R134a较为理想的替代制冷剂,无毒、化学性质稳定,ODP值为0,GWP值较低[18]。R236fa被认为是离心式冷水机组有前途的替代制冷剂,不可燃,ODP值为0,传热系数较高,可替代2, 2-二氯化-1, 1, 1-三氟乙烷(2, 2-dichloro-1, 1, 1-trifluoroethane, R123)和1, 2-二氯化-1, 1, 2, 2-四氟乙烷(1, 2-dichloro-1, 1, 2, 2-tetrafluoroethane, R114)[15]。R1234ze(E)和R236fa基本热物性参数如表 4所示。与液相比定压热容测量相同,仿真过程选择R134a为参比流体。对R1234ze(E)在压力1.56~4.53 MPa、温度310.15~365.15 K范围内34个点进行仿真;对R236fa在压力1.48~5.41 MPa、温度315.15~365.15 K范围内32个点进行仿真。R1234ze(E)和R236fa通过CFD修正后的结果如表 5和6所示。
|
|
表 4 R1234ze(E), R236fa和R134a基本热物性参数 Table 4 Thermophysical properties of R1234ze(E), R236fa and R134a |
|
|
表 5 R1234ze(E)比定压热容修正结果 Table 5 Modified results of the isobaric heat capacity of R1234ze(E) |
|
|
表 6 R236fa比定压热容修正结果 Table 6 Modified results of the isobaric heat capacity of R236fa |
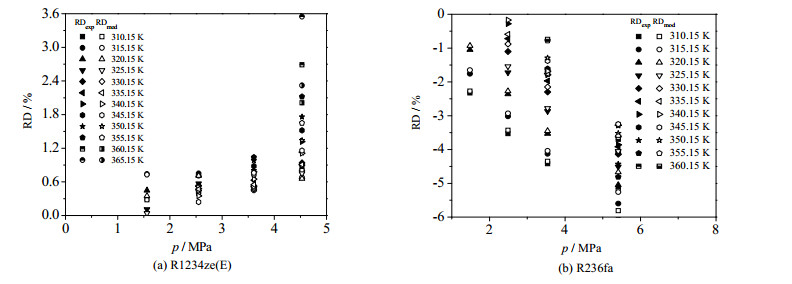
从表 5中可以发现,R1234ze(E)修正后的比定压热容值与EES计算值之间平均绝对偏差AAD从修正前0.91%下降至0.75%,最大偏差MAD从3.55%减至3.22%。从表 6中可以发现,R236fa修正后的比定压热容平均绝对偏差AAD从修正前3.04%降至2.66%,最大偏差MAD从6.08%减至5.81%。R1234ze(E)和R236fa修正前后的比定压热容与EES计算值之间偏差RD如图 5所示。
|
图 5 R1234ze(E)和R236fa实验值、修正值和EES计算值之间偏差(RD%) Fig.5 Deviations among experimental, modified and EES calculation of R1234ze(E) and R236fa (RD%) |
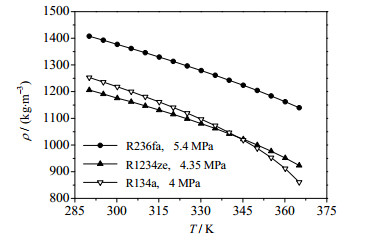
R1234ze(E)、R236fa和R134a分别在5.4、4.35、4 MPa下从293.15 K升温到365.15 K时密度变化情况如图 6所示。从图 6中可以看出,在初始温度293.15 K加热到温度365.15 K时,R1234ze(E)、R236fa和R134a,其密度变化幅度分别为23.43%、19.04%和31.33%,远大于前述苯和水的密度变化幅度。故而,在测量池与压力平衡罐之间呈现更强烈的对流现象,导致ΔVsample和ΔVref变化幅度更大。同时,由于样本流体ΔVsample与参比流体ΔVref变化并非完全同步,由式(4)容易理解这时对流对测量误差的影响会更显著。这些可能是通过CFD修正R1234ze(E)和R236fa液相比定压热容有更好效果的主要原因。
|
图 6 R1234ze(E)、R236fa和R134a密度随温度变化 Fig.6 Density profiles of R1234ze(E), R236fa and R134a as a function of temperature |
对一套基于C80量热仪并可在比较宽广的温度和压力范围内开展低沸点流体液相比定压热容快捷、高效测量的装置进行了比较深入的工作机理分析,建立了其数学物理修正模型。基于数学物理修正模型,应用COMSOL软件开展了CFD仿真分析,并用于修正2种具有良好替代潜力的新型环保制冷工质R1234ze(E)和R236fa的液相比定压热容。通过研究得出以下结论:
(1) 通过发展数学物理修正模型,开展CFD仿真可有效减少对流现象对准稳态量热法测量低沸点流体液相比定压热容精度的影响,从而显著提高测量精度;
(2) 把CFD仿真方法用于修正2种典型低沸点流体R1234ze(E)和R236fa的液相比定压热容,获得了更高精度的比定压热容数据;
更深入探索其内在工作机理,发展数学物理修正模型,通过CFD仿真研究更多因素对准稳态量热法测量低沸点流体液相比定压热容精度的影响,可望进一步提高其测量精度,可为低沸点流体高精度比定压热容数据获取提供新思路。
| 符号说明: | |||
| AAD | —平均绝对偏差,无量纲 | V | —体积,m3 |
| cp | —比定压热容,kJ·kg-1·K-1 | v | —分速度,m·s-1 |
| F | —体积力,kg·m·s-2 | ▽ | —拉普拉斯算子 |
| HF | —热流,W·m-2 | ρ | —密度,kg·m-3 |
| i, N | —试验点数,无量纲 | 下标 | |
| k | —导热系数,W·m-1·K-1 | blank | —空白组 |
| MAD | —最大绝对偏差,无量纲 | exp | —实验值 |
| n | —法向单位矢量 | hydro | —静压 |
| p | —压力,Pa | Initial | —初始条件 |
| Q | —热量,J | ees | — EES数据库值 |
| q | —热流密度矢量,J·m-2·s-1 | mod | —模型修正值 |
| RD | —相对偏差,无量纲 | ref | —参照组 |
| T | —温度,K | sample | —样本组 |
| τ | —时间,s | r, θ, z | —坐标系 |
| u | —速度,m·s-1 | vd | —黏性耗散 |
| [1] |
秦大河. IPCC第五次评估报告第一工作组报告的亮点结论[J]. 气候变化研究进展, 2014, 10(1): 1-6. QIN D H. Highlights of the first working group report of the IPCC Fifth Assessment Report[J]. Advances in Climate Change Research, 2014, 10(1): 1-6. DOI:10.3969/j.issn.1673-1719.2014.01.001 |
| [2] |
陈琪, 闫继位, 陈光明, 等. 新型制冷剂R1234yf/R134a可燃性实验研究[J]. 太阳能学报, 2016, 37(1): 152-156. CHEN Q, YAN J W, CHEN G M, et al. Experimental study on the flammability of a new type of refrigerant R1234yf/R134a[J]. Acta Energiae Solaris Sinica, 2016, 37(1): 152-156. DOI:10.3969/j.issn.0254-0096.2016.01.024 |
| [3] |
MCLINDEN M O, BROWN J S, BRIGNOLI R, et al. Limited options for low - global - warming-potential refrigerants[J]. Nature Communications, 2017, 8(2): 14476. |
| [4] |
LIU Y, ZHAO X M, Lv S H. Heat capacity of isobutane in liquid phase at temperatures from 303K to 413K and pressures up to 12MPa[J]. Journal of Chemical Thermodynamics, 2017, 111(8): 265-270. |
| [5] |
LIU Y, ZHAO X M. Measurement of the heat capacity of R1233zd(E)[J]. International Journal of Refrigeration, 2017, 86(11): 127-132. |
| [6] |
TANAKA H, FUJIWARA N, SATO H. Isobaric heat capacity of Liquid 1, 1, 1, 3, 3 - Pentafluoropropane (R245fa) by flow calorimeter from 278 K to 343 K[J]. Journal of Chemical & Engineering Data, 2015, 60(12): 3594-3599. |
| [7] |
TANAKA K, HIGASHI Y, AKASAKA R. Measurements of the isobaric heat capacity and density for HFO-1234yf in the liquid state[J]. Journal of Chemical & Engineering Data, 2010, 55(2): 901-903. |
| [8] |
TANAKA K, TAKAHASHI G, HHIGASHI Y. Measurements of the isobaric heat capacities for trans-1, 3, 3, 3-Tetrafluoropropene (HFO-1234ze(E)) in the liquid phase[J]. Journal of Chemical & Engineering Data, 2010, 55(6): 2267-2270. |
| [9] |
HYKRDA R, COXAM J Y, MAJER V. Experimental determination of isobaric heat capacities of R227ea(CF3CHFCF3) from 223 to 283 K at pressures up to 20MPa[J]. International Journal of Thermophysics, 2004, 25(6): 1677-1694. DOI:10.1007/s10765-004-7729-2 |
| [10] |
GAO N, JIANG Y Y, WU J, et al. Measurements of the isobaric heat capacity of R1234yf in liquid phase at temperatures from 305 K to 355 K and pressures up to 5 MPa[J]. Fluid Phase Equilibria, 2014, 376(12): 64-68. |
| [11] |
GAO N, CHEN G, LI R, et al. Isobaric heat capacities of R245fa and R236fa in liquid phase at temperatures from (315 to 365) K and pressures up to 5.5 MPa[J]. Journal of Chemical Thermodynamics, 2015, 90(11): 46-50. |
| [12] |
HE Y J, LI R, GAO N, et al. Isobaric heat capacity of HFC-161 in the liquid phase at temperatures up to 360.15 K and pressures up to 5.5 MPa[J]. Journal of Chemical & Engineering Data, 2015, 60(8): 2226-2231. |
| [13] |
GAO N, CHEN G, LI R, et al. Measurements of the isobaric heat capacity of pressurized liquid trans-1, 3, 3, 3-tetrafluoropropene[R1234ze(E)] by scanning calorimetry[J]. Journal of Thermal Analysis & Calorimetry, 2015, 122(3): 1469-1476. |
| [14] |
HE Y J, GAO N, etal. Liquid isobaric heat capacity measuring device and method capable of self-balancing pressure: CN, ZL201410064752.4[P], 2014-02-25.
|
| [15] |
高能, 蒋云云, 何一坚. 一种制冷剂液态比定压热容的测量装置[J]. 工程热物理学报, 2015, 36(4): 709-713. GAO N, JIANG Y Y, HE Y J. A measuring system for the isobaric heat capacity of liquid refrigerants[J]. Journal of Engineering Thermophysics, 2015, 36(4): 709-713. |
| [16] |
胡哲, 江劲勇, 路桂娥, 等. 某型改性双基推进剂比热容随温度变化规律研究[J]. 军械工程学院学报, 2015(4): 43-46. HU Z, JIANG J Y, LU G E, et al. Temperature dependence of isobaric heat capacity of one modified double-base propellant[J]. Journal of Ordnance Engineering College, 2015(4): 43-46. DOI:10.3969/j.issn.1008-2956.2015.04.009 |
| [17] |
KLEIN, S A, ALVARADO, F L, EES - Engineering Equation Solver[DB], Middleton, WI: F-Chart Software.
|
| [18] |
邱金友. 新型制冷剂R1234ze(E)及其混合工质研究进展[J]. 制冷学报, 2015, 36(3): 9-16. QIU J Y. A study on new refrigerant R1234ze(E) and its mixtures[J]. Journal of Refrigeration, 2015, 36(3): 9-16. DOI:10.3969/j.issn.0253-4339.2015.03.009 |




