2. 西安交通大学 能源与动力学院,陕西 西安 710049
2. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
在2015年,中国的煤炭消费量占所有的一次能源的66%[1],这一数据仍然处在一个较高的水平,实现煤炭的清洁高效转化越来越受到关注。国家有关能源政策倾向支持使煤炭得到清洁利用的技术[2]。煤气化是煤炭洁净利用的重要方面,也是煤化工工艺的龙头技术,其中水煤浆的加压气化技术相对成熟可靠,是国内技术引进、研究、应用和自主化攻关的主流技术[3]。为了提高水煤浆的气化效率,国内外很多学者研究了提高水煤浆气化效率的途径[4-6],其中夏德宏等[4]提出,对进入炉前的水煤浆进行一定程度的预热,适当提高入口温度,可以使水煤浆在气化炉中更容易雾化,气化过程更加稳定,气化效率更高。
高浓度的水煤浆是一种非牛顿流体,非牛顿流体的换热通常面临流体的表观黏度大、压力损失大、容易结垢等问题[7]。近年来,关于非牛顿流体在换热器中流动和换热性能的研究方兴未艾。CRESPÌ-LLORENS等[8]实验研究了具有非牛顿流体特征的1%质量分数的羧甲基纤维素(CMC)的水溶液在刮板式换热器壳侧的流动和换热性能,发现提高刮擦运动功率可以增强非牛顿流体的传热,同时减少结垢;何振斌等[9]通过CFD研究了3%质量分数的CMC水溶液在具有椭圆管的螺旋折流板换热器壳侧的流动和换热性能,计算结果表明椭圆管换热器的表面传热系数在不同的工况下比圆管换热器提高14.7%~16.4%,壳侧摩擦系数降低29.2%~36.9%;RIOS-IRIBE等[10]通过数值计算研究了通过板式换热器加热番茄酱的可行性,得到了番茄酱在板式换热器中Nu数和摩擦系数的经验关联式。但是这些研究主要集中在CMC水溶液和食品工业中的一些流体在换热器中的流动和换热表现,目前涉及到水煤浆在换热器中的流动和换热表现的研究还比较少。
相比于传统的弓形折流板换热器,螺旋折流板换热器具有壳程阻力小、壳程传热系数高以及能有效抑制壳程污垢累积沉淀、防止流体诱导振动、可实现长周期高效率运行等诸多优点[11-13],已经在石油化工等行业广泛应用。近年来国内外学者对螺旋折流板的形式,搭接度和螺旋角等结构参数进行了研究。TAHER等[14]研究了在螺旋角为40°时,不同搭接度对螺旋折流板换热器壳侧流动换热性能的影响,在螺旋角一定时,大的搭接度会让压降增大,换热系数提高;杜婷婷等[15]利用Taguchi方法定量分析了螺旋角、搭接度、换热管直径、布管方式以及管间距对壳侧流动换热性能的影响;WEN等[16]采用结合Kriging响应面的多目标遗传算法对螺旋折流板换热器的换热要求和操作费用进行了优化。但是这些研究大多集中在工作介质为小黏度的牛顿流体的情况,对于类似水煤浆的非牛顿流体在螺旋折流板换热器中的流动和换热表现,相关的研究还比较匮乏。
基于水煤浆预热中水煤浆表观黏度大、压降大和易结垢的换热困难和螺旋折流板换热器壳程阻力小、壳程传热系数高、可以减少结垢的优点,本文采用数值计算的方法,选择非牛顿流体Bingham模型,比较了当管侧通高温导热油来预热壳侧质量分数wB=62%水煤浆时,弓形折流板换热器和螺旋折流板换热器的流动换热性能。分析了螺旋折流板换热器作为水煤浆预热器的可行性以及螺旋角在18°~40°变化和搭接度在0%~50%变化时对水煤浆螺旋折流板预热器的流动换热性能的影响。
2 模型 2.1 几何模型本文采用的螺旋折流板换热器的折流板形式为应用最广泛的四板型扇形折流板,即一个螺旋周期内由4块扇形折流板组成,其几何参数如表 1所示,管束示意图如图 1所示。螺旋折流板换热器的几何模型由三维建模软件生成,管子、筒体和折流板均采用无厚度的面,且为了简化模型,模型忽略了各种间隙漏流。
|
|
表 1 螺旋折流板换热器模型参数 Table 1 Model parameters of STHXsHB |

|
图 1 螺旋折流板换热器管束示意图 Fig.1 Schematic diagram of tube bundle of STHXsHB |
为了比较弓形折流板换热器和螺旋折流板换热器作为水煤浆预热器的流动换热性能,本文还构建了相应结构下的弓形折流板换热器的几何模型,其几何参数如表 2所示,管束示意图如图 2所示,其折流板间距与27°螺旋角,50%搭接度的螺旋折流板换热器的螺距相等。
|
|
表 2 弓形折流板换热器模型参数 Table 2 Model parameters of STHXsSB |

|
图 2 弓形折流板换热器管束示意图 Fig.2 Schematic diagram of tube bundle of STHXsSB |
本次数值计算中螺旋折流板换热器和弓形折流板换热器的壳侧工质为水煤浆,根据文献调研,水煤浆在低浓度下可视为牛顿流体,当煤质量浓度达到50%及以上时表现为非牛顿流体特性[17],本文中水煤浆质量浓度为62%,视为非牛顿流体计算。
对于非牛顿流体,常用的本构关系式如下[18]:
| $ \tau ={{\tau }_{0}}+k{{\gamma }^{n}} $ | (1) |
式中:τ为剪切应力,Pa;τ0为屈服剪切应力,Pa;γ为剪切速率,s-1,k为稠度系数;n为流动性系数。
当τ0=0,n=1时为牛顿模型:
| $ \tau =k\gamma $ | (2) |
当τ0=0,n≠1时为幂律模型:
| $ \tau =k{{\gamma }^{n}} $ | (3) |
其中n < 1为假塑性流体幂律模型,n > 1为胀塑性流体幂律模型。
当τ0≠0,n=1时为宾汉(Bingham)模型:
| $ \tau ={{\tau }_{0}}+k\gamma $ | (4) |
当τ0≠0,n≠1时为屈服幂律模型:
| $ \tau ={{\tau }_{0}}+k{{\gamma }^{n}} $ | (5) |
其中n < 1为假塑性流体屈服幂律模型,n > 1为胀塑性流体屈服幂律模型。
谢东等[17]根据实验数据分别采用Bingham模型、屈服幂律模型、Casson模型进行拟合,发现相比较为简单的Bingham模型的拟合度已经达到了0.996 4,所以本文采用Bingham模型作为水煤浆的流变模型。该模型中,wB=62%的水煤浆的剪切速率与剪切应力之间的关系可以用下式表示:
| $ \tau =60.06+0.202\ 6\gamma $ | (6) |
螺旋折流板换热器和弓形折流板换热器的几何模型由三维建模软件生成,管侧网格使用扫掠方法生成,考虑到壳侧几何的复杂程度,壳侧网格采用非结构化网格。为提高网格质量,对生成的网格进行自适应处理。同时在模拟之前验证了网格独立性,如图 3所示,当27°螺旋角,50%搭接度的螺旋折流板换热器的网格量增加到9 075 140以上时,壳侧温升和壳侧单位压降温升偏差在可接受范围,考虑计算的速度和精度,最终螺旋折流板换热器网格单元数的范围为7 353 408到9 207 164,弓形折流板换热器网格单元数为10 701 441。螺旋折流板换热器一个周期的折流板网格和轴向网格和如图 4所示,弓形折流板换热器的相邻两块的折流板网格和轴向网格如图 5所示。

|
图 3 网格无关性验证 Fig.3 Results of grid independence tests |

|
图 4 螺旋折流板换热器网格示意图 Fig.4 Schematic diagram of SHHXsHB mesh |

|
图 5 弓形折流板换热器网格示意图 Fig.5 Schematic diagram of SHHXsSB mesh |
由于螺旋折流板换热器中壳侧流体在主流流动有强烈的旋转,同时流体流动过程中还存在局部二次流和剪切应力梯度剧烈变化的区域,即流动表现出对流线弯曲的敏感性及高度的各向异性,因此湍流模型采用经过重整化群处理的RNG κ-ε模型,有效提升了高应变率及强流线弯曲时的计算精度[19-20]。
RNG κ-ε模型的基本方程包括质量、动量、能量及κ-ε方程,它们的表达式如下[21]:
连续性方程:
| $ \frac{\partial }{\partial {{x}_{{\rm{i}}}}}\left( \rho {{u}_{{\rm{i}}}} \right)=0 $ | (7) |
动量方程:
| $ \frac{\partial }{\partial {{x}_{\text{i}}}}\left( \rho {{u}_{\text{i}}}{{u}_{\text{k}}} \right)=\frac{\partial }{\partial {{x}_{\text{i}}}}\left( \mu \frac{\partial {{u}_{\text{k}}}}{\partial {{x}_{\text{i}}}} \right)-\frac{\partial P}{\partial {{x}_{\text{k}}}} $ | (8) |
能量方程:
| $ \frac{\partial }{\partial {{x}_{\text{i}}}}\left( \rho {{u}_{\text{i}}}t \right)=\frac{\partial }{\partial {{x}_{\text{i}}}}\left( \frac{\kappa }{{{c}_{\text{p}}}}\frac{\partial t}{\partial {{x}_{\text{i}}}} \right) $ | (9) |
湍流动能方程:
| $ \frac{\partial }{\partial t}(\rho \kappa )+\frac{\partial }{\partial {{x}_{\text{i}}}}(\rho \kappa {{u}_{\text{i}}})=\frac{\partial }{\partial {{x}_{\text{j}}}}\left[ {{\alpha }_{k}}{{\mu }_{\text{eff}}}\frac{\partial \kappa }{\partial {{x}_{\text{i}}}} \right]+{{G}_{\text{k}}}-\rho \varepsilon $ | (10) |
湍流能量耗散方程:
| $ \frac{\partial }{\partial t}(\rho \varepsilon )+\frac{\partial }{\partial {{x}_{\text{i}}}}(\rho \varepsilon {{u}_{\text{i}}})=\frac{\partial }{\partial {{x}_{\text{j}}}}\left( {{\alpha }_{\varepsilon }}{{\mu }_{\text{eff}}}\frac{\partial \varepsilon }{\partial {{x}_{\text{j}}}} \right)+C_{1\varepsilon }^{*}\frac{\varepsilon }{\kappa }{{G}_{\text{k}}}-{{C}_{2\varepsilon }}\rho \frac{{{\varepsilon }^{2}}}{\kappa } $ | (11) |
其中κ为湍流动能,ε为湍流耗散率,湍动能产生项
当流体为不可压缩的非牛顿流体时,剪切应力τ与形变张量速率D的关系为[22]:
| $ \tau =\mu D $ | (12) |
上式中D可由下式计算:
| $ D=\left( \frac{\partial {{u}_{\text{j}}}}{\partial {{x}_{\text{i}}}}+\frac{\partial {{u}_{\text{i}}}}{\partial {{x}_{\text{j}}}} \right) $ | (13) |
对于一些非牛顿流体,剪切应力τ也可以用非牛顿黏度η表示为:
| $ \tau =\eta \left( D \right)D $ | (14) |
由式(12)(14)可知,对于非牛顿流体:
| $ \mu =\eta \left( D \right) $ | (15) |
其中η是关于D的方程,但在常用的流变模型中,η是关于剪切速率γ的方程,γ与D的关系为:
| $ \gamma =\sqrt{\frac{1}{2}D:D} $ | (16) |
由(15)(16)可知,非牛顿流体任意状态下的动力黏度μ都可以通过D表示。特别的,对于本文所研究的具有Bingham模型特征的非牛顿流体,有:
| $ \mu =\eta \left( D \right)=\frac{{{\tau }_{0}}}{\gamma }+k{{\gamma }^{n-1}}=\frac{{{\tau }_{0}}}{\sqrt{\frac{1}{2}D:D}}+k{{\left( \sqrt{\frac{1}{2}D:D} \right)}^{n-1}} $ | (17) |
在计算时,管侧流体为导热油,管侧入口为速度入口,流速为1.2 m·s-1,温度为373 K;管侧出口为压力出口。壳侧流体为wB=62%水煤浆,壳侧入口为速度入口,水煤浆的体积流量在6 ~18 m3·h-1,温度为293 K;壳侧出口为压力出口。其他的各固体壁面定义为不可渗透、无滑移绝热条件。压力速度耦合为SIMPLE算法,采用一阶迎风格式求解质动量方程、湍动能方程及湍流能量耗散方程,采用二阶迎风格式求解能量方程,定义了能量方程的收敛残差为10-6,其他方程收敛条件为残差小于10-3。
3 计算结果与分析 3.1 数值计算的有效性验证和壳侧流场分析采用本文中的流变模型,将温度为300 K,wB=62%的水煤浆通过长度为1.0 m,管径为11.4 mm的直管段,直管段的管壁温度为600 K。将数值计算出的压降值与文献[23]中介绍的理论解法计算出的压降值相比较,如图 6所示。由图可知,进出口压降的模拟值和理论值吻合较好。在水煤浆流速在0.5~3.0 m·s-1时,进出口压降相对误差的范围为0.67%~4.54%。

|
图 6 计算压降和理论压降的对比 Fig.6 Comparison of simulated and theoretical pressure drops |
将数值计算得到的距离入口0.2 m处的对流传热系数与根据文献[24]中介绍的关联式计算出的对流传热系数相比较,如图 7所示。由图可知,距离入口0.2 m处的对流传热系数的模拟值和关联式计算值吻合较好。在水煤浆流速在0.5~3.0 m·s-1时,距离入口0.2 m处的对流传热系数相对误差为6.81%~8.69%,说明了该数值方法是可靠的。

|
图 7 计算对流传热系数和实验对流传热系数的对比 Fig.7 Comparison of simulated and experimental heat transfer coefficients |
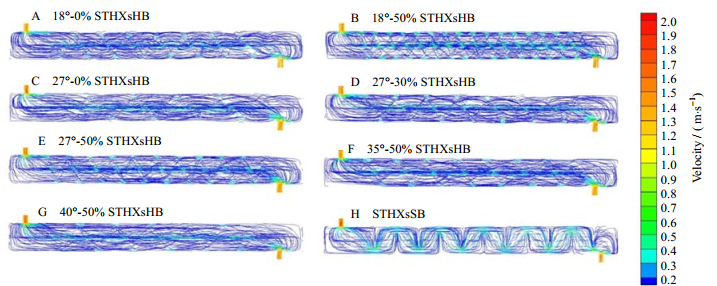
wB=62%的水煤浆流过不同螺旋角和搭接度的螺旋折流板换热器和弓形折流板换热器壳侧时的流线如图 8所示。可以看到,螺旋角在18°~40°、搭接度在0%~50%变化,螺旋折流板换热器可以使壳侧的水煤浆流体产生较好的连续螺旋流动,水煤浆在壳侧流速比较均匀,流动比较连续。而水煤浆在弓形折流板换热器的壳侧的速度分布较不均匀,在弓形板缺口处流速很高,增大了压力损失,在其余部位尤其是折流板背部流速较低,容易形成流动的死区。
|
图 8 水煤浆流过不同换热器壳侧时的流线图 Fig.8 Streamline diagrams of different preheating heat exchangers shell with CWS |
因为非牛顿流体黏度往往较大,带来了较大的压降ΔP,而且对于水煤浆气化工艺而言,要求水煤浆经过预热换热器的压降必须符合工艺要求[25],工业生产希望在尽量小的压降条件下获得尽量多的温升,因此对于水煤浆预热器,评价换热器的流动和换热性能,除了温升ΔT以外,压降ΔP也是一个十分重要的评价指标。综合考虑温升和压降的影响和水煤浆气化工艺的实际要求,以单位壳侧压降的温升ΔT/ΔP作为综合评价水煤浆预热器的指标。
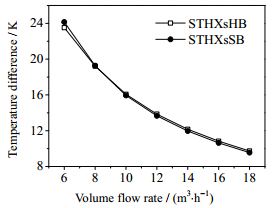
在水煤浆的体积流量在6~18 m3·h-1时,考查了水煤浆流过27°螺旋角,50%搭接度的螺旋折流板换热器和弓形折流板换热器的温升和压降,如图 9和10所示。计算采用的弓形折流板换热器的折流板间距与27°螺旋角,50%搭接度的螺旋折流板换热器的螺距相同。从图中可以看出,在相同壳侧体积流量下,水煤浆在螺旋折流板换热器和弓形折流板换热器中的温升基本相同,但水煤浆在螺旋折流板换热器中的压降相比弓形折流板换热器大大降低。在计算的体积流量范围内,27°螺旋角,50%搭接度的螺旋折流板换热器壳侧的压降相比弓形折流板换热器下降了31.13%~35.75%。
|
图 9 两种换热器温升的比较 Fig.9 Comparison of temperature difference between two heat exchangers |

|
图 10 两种换热器压降的比较 Fig.10 Comparison of pressure drops between two heat exchangers |
因为两种换热器型式的不同对水煤浆温升影响很小,而水煤浆在螺旋折流板换热器中的压降相比弓形折流板换热器大大降低。所以以单位壳侧压降的温升ΔT/ΔP作为综合评价的指标,螺旋折流板换热器在预热水煤浆时的性能优于弓形折流板换热器。在计算的体积流量范围内,27°螺旋角,50%搭接度的螺旋折流板换热器壳侧的ΔT/ΔP相比弓形折流板换热器提高了47.91%~52.31%,如表 3所示。
|
|
表 3 两种换热器ΔT/ΔP比较 Table 3 Comparison of ΔT/ΔP values of two heat exchangers |
当螺旋折流板换热器的搭接度为50%,分析了螺旋角的变化对螺旋折流板换热器内壳侧温升和壳侧压降的影响,如图 11所示。在水煤浆体积流量较大时,在相同壳侧体积流量下的温升随螺旋角的增大而下降,具有较小螺旋角的换热器产生的温升较大,这样的规律也与之前关于螺旋折流板换热器的大多数研究相一致[15, 26]。但是当水煤浆的体积流量较小时,情况却刚好相反,具有较大螺旋角的换热器反而能产生较大的温升。

|
图 11 螺旋角对温升的影响 Fig.11 Effects of helical angle on temperature difference |
为了研究在水煤浆体积流量较小时,具有较小螺旋角的换热器不能产生预想中的较大温升的原因,查看了在水煤浆的入口流速ν分别为0.85和7 m·s-1时,水煤浆流过27°螺旋角、50%搭接度的换热器壳侧中间截面(z=1.070 m)时的流速分布图,如图 12和13所示。

|
图 12 流速0.85 m·s-1时中间截面流速分布 Fig.12 Velocity distribution at the middle cross section under flow rate of 0.85 m·s-1 |
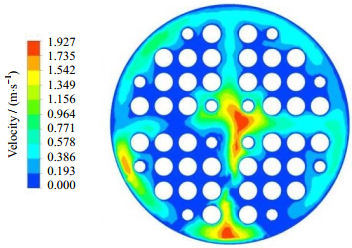
|
图 13 流速7 m·s-1时中间截面流速分布 Fig.13 Velocity distribution at the middle cross section under flow rate of 7 m·s-1 |
对比图 12和13可以看到,在水煤浆的入口流速ν= 7 m·s-1时,水煤浆在截面的流速分布较为均匀,大部分水煤浆流过了换热管;而在水煤浆的入口流速ν= 0.85 m·s-1时,水煤浆在截面中央的中心漏流区的流速远远高于在截面四周的流速,更多的水煤浆没有流过换热管而是从中心漏流区流过,这就是水煤浆的体积流量较小时,较小的螺旋角未能产生较大的温升的原因。
同时,从图 11中还可以看到,螺旋角的变化对水煤浆温升的影响并不明显。在水煤浆的体积流量为18 m3·h-1时,40°螺旋角,50%搭接度的螺旋折流板换热器壳侧的温升相比18°螺旋角,50%搭接度的螺旋折流板换热器只下降了3.30%。
图 14为具有不同螺旋角的换热器内壳侧压降随水煤浆体积流量的变化,在相同壳侧体积流量下,随着螺旋角的增大,水煤浆在壳侧的压降逐渐减小。同时,螺旋角的变化对壳侧压降的影响十分明显,尤其是在与螺旋角对壳侧温升的影响相比较时。计算的体积流量范围内,40°螺旋角,50%搭接度的螺旋折流板换热器壳侧的压降相比18°螺旋角,50%搭接度的螺旋折流板换热器下降了35.88%~39.06%。

|
图 14 螺旋角对压降的影响 Fig.14 Effects of helical angle on pressure drop |
以单位壳侧压降的温升ΔT/ΔP作为综合评价的指标,较大螺旋角的螺旋折流板换热器更有优势。计算的体积流量范围内,40°螺旋角,50%搭接度的螺旋折流板换热器壳侧的ΔT/ΔP相比18°螺旋角,50%搭接度的螺旋折流板换热器提高了53.82%~63.97%,如表 4所示。
|
|
表 4 不同螺旋角的换热器ΔT/ΔP比较 Table 4 Comparison of ΔT/ΔP values of exchangers with different helical angles |
当螺旋折流板换热器的螺旋角为27°时,分析了搭接度的变化对换热器内壳侧温升和壳侧压降的影响,如图 15所示。在水煤浆体积流量较大时,不同搭接度对于水煤浆温升的影响很小。但是当水煤浆的体积流量较小时,情况又有所不同,具有较小搭接度的换热器反而能产生较大的温升,这一情况出现的原因也是由于在水煤浆的体积流量较小时,中心漏流的情况会更加严重。

|
图 15 搭接度对温升的影响 Fig.15 Effects of overlapped degree on temperature difference |
图 16为具有不同搭接度的换热器内壳侧压降随水煤浆体积流量的变化,在相同壳侧体积流量下,随着搭接度的增大水煤浆在壳侧的压降逐渐增大。同时,搭接度的变化对水煤浆进出口压降的影响比较明显。在计算的体积流量范围内,27°螺旋角,50%搭接度的螺旋折流板换热器壳侧的压降相比27°螺旋角,0%搭接度的螺旋折流板换热器增加了17.20%~20.31%。

|
图 16 搭接度对压降的影响 Fig.16 Effects of overlapped degree on pressure drop |
因为较大的搭接度在对水煤浆温升影响很小的同时会产生较大压降提高。所以以单位壳侧压降的温升ΔT/ΔP作为综合评价的指标,较小的搭接度的螺旋折流板换热器更有优势。在计算的体积流量范围内,27°螺旋角,0%搭接度的螺旋折流板换热器壳侧的ΔT/ΔP相比27°螺旋角,50%搭接度的螺旋折流板换热器提高了16.83%~24.67%,如表 5所示。
|
|
表 5 不同搭接度的换热器ΔT/ΔP比较 Table 5 Comparison of ΔT/ΔP values of exchangers with different overlapped degrees |
对进入炉前的水煤浆进行预热,可以使水煤浆在气化炉中气化效率更高,更节能环保。本文采用数值计算的方法,应用Bingham流变模型,对比了螺旋折流板换热器和弓形折流板换热器预热水煤浆的流动换热性能,并对螺旋角、搭接度对水煤浆预热器的流动换热性能的影响进行了研究,得到了以下结论:
(1) 相比于弓形折流板换热器,螺旋折流板换热器可以让水煤浆在壳侧流速分布更加均匀,流动更加连续,产生较好的螺旋状流动,使压降大大降低,更适合预热水煤浆。以ΔT/ΔP作为综合评价水煤浆预热器的指标,螺旋折流板换热器的ΔT/ΔP相比相应结构参数的弓形折流板换热器提高了47.91%~52.31%。
(2) 随着螺旋角的增大,水煤浆温升变化不大但是压降明显降低,以ΔT/ΔP为评价指标,40°螺旋角,50%搭接度的换热器的换热性能相比18°螺旋角,50%搭接度的换热器提高了53.82%~63.97%。
(3) 随着搭接度的增大,水煤浆温升变化很小但是压降显著增加,以ΔT/ΔP为评价指标,27°螺旋角,0%搭接度的换热器的换热性能相比27°螺旋角,50%搭接度的换热器提高了16.83%~24.67%。
(4) 综合考虑螺旋角和搭接度对换热器性能的影响,大螺旋角和小搭接度的螺旋折流板换热器更适合预热水煤浆。在螺旋角18°~40°,搭接度0%~50%,40°螺旋角,0%搭接度的换热器最适合预热水煤浆。
符号说明:
|
|
| [1] |
MUSA S D, TANG Z, IBRAHIM A O, et al. China's energy status:a critical look at fossils and renewable options[J]. Renewable & Sustainable Energy Reviews, 2017, 81(2): 2281-2290. |
| [2] |
高聚忠. 煤气化技术的应用与发展[J]. 洁净煤技术, 2013, 19(1): 65-71. GAO J Z. Application and development of coal gasification technologies[J]. Clean Coal Technology, 2013, 19(1): 65-71. |
| [3] |
孙漾, 顾幸生. 水煤浆气化装置操作优化技术及其应用[J]. 化工学报, 2012, 63(9): 2799-2804. SUN Y, GU X S. Coal water slurry gasification unit operation optimization technology and its application[J]. CIESC Journal, 2012, 63(9): 2799-2804. DOI:10.3969/j.issn.0438-1157.2012.09.020 |
| [4] |
夏德宏, 唐献红, 王世均. 水煤浆预热对燃烧的影响[J]. 冶金能源, 1992, 11(5): 30-31. XIA D H, TANG X H, WANG S J. Influence of preheating on CWS combustion[J]. Energy for Metallurgical Industry, 1992, 11(5): 30-31. |
| [5] |
AIUCHI K, MORIYAMA R, TAKEDA S, et al. A pre-heating vaporization technology of coal-water-slurry for the gasification process[J]. Fuel Processing Technology, 2007, 88(4): 325-331. DOI:10.1016/j.fuproc.2004.10.010 |
| [6] |
ZHANG J, ZHOU Z, MA L, et al. Efficiency of wet feed IGCC (integrated gasification combined cycle) systems with coal-water slurry preheating vaporization technology[J]. Energy, 2013, 51(1): 137-145. |
| [7] |
CRESP -LLORENS D, VICENTE P, VIEDMA A. Flow pattern of non-Newtonian fluids in reciprocating scraped surface heat exchangers[J]. Experimental Thermal & Fluid Science, 2016, 76(9): 306-323. |
| [8] |
CRESP -LLORENS D, VICENTE P, VIEDMA A. Experimental study of heat transfer to non-Newtonian fluids inside a scraped surface heat exchanger using a generalization method[J]. International Journal of Heat and Mass Transfer, 2018, 118(3): 75-87. |
| [9] |
HE Z, FANG X, ZHANG Z, et al. Numerical investigation on performance comparison of non-Newtonian fluid flow in vertical heat exchangers combined helical baffle with elliptic and circular tubes[J]. Applied Thermal Engineering, 2016, 100(3): 84-97. |
| [10] |
RIOS-IRIBE E Y, CERVANTES-GAXIOLA M E, RUBIO-CASTRO E, et al. Heat transfer analysis of a non-Newtonian fluid flowing through a Plate Heat Exchanger using CFD[J]. Applied Thermal Engineering, 2016, 101(3): 262-272. |
| [11] |
WANG Q, ZENG M, MA T, et al. Recent development and application of several high-efficiency surface heat exchangers for energy conversion and utilization[J]. Applied Energy, 2014, 135(12): 748-777. |
| [12] |
王斯民, 肖娟, 王家瑞, 等. 基于流固耦合理论的螺旋折流板换热器结构优化研究[J]. 高校化学工程学报, 2017, 31(3): 539-546. WANG S M, XIAO J, WANG J R, et al. Structural optimization of shell-tube heat exchanger with helical baffles based on fluid-structure interaction[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(3): 539-546. DOI:10.3969/j.issn.1003-9015.2017.00.018 |
| [13] |
WEN J, YANG H Z, WANG S M, et al. Experimental investigation on performance comparison for shell-and-tube heat exchangers with different baffles[J]. International Journal of Heat & Mass Transfer, 2015, 84(5): 990-997. |
| [14] |
TAHER F N, MOVASSAG S Z, RAZMI K, et al. Baffle space impact on the performance of helical baffle shell and tube heat exchangers[J]. Applied Thermal Engineering, 2012, 44(11): 143-149. |
| [15] |
DU T T, DU W H, CHE K, et al. Parametric optimization of overlapped helical baffled heat exchangers by Taguchi method[J]. Applied Thermal Engineering, 2015, 85(6): 334-339. |
| [16] |
WEN J, YANG H Z, JIAN G P, et al. Energy and cost optimization of shell and tube heat exchanger with helical baffles using Kriging metamodel based on MOGA[J]. International Journal of Heat and Mass Transfer, 2016, 98(7): 29-39. |
| [17] |
谢东.水煤浆流变特性及其检测技术研究[D].武汉: 华中科技大学, 2010. XIE D. Research on rheological characteristics of coal water slurry and its measurement technologies[D]. Wuhan: Huazhong University of Science and Technology, 2010. |
| [18] |
代淑兰, 陈良勇, 代少辉. 水煤浆的流变特性研究进展[J]. 锅炉技术, 2010, 41(3): 76-80. DAI S L, CHEN L Y, DAI S H. Advances in research on rheological behaviour of coal-water slurries[J]. Boiler Technology, 2010, 41(3): 76-80. DOI:10.3969/j.issn.1672-4763.2010.03.018 |
| [19] |
ZHANG J F, LI B, HUANG W J, et al. Experimental performance comparison of shell-side heat transfer for shell-and-tube heat exchangers with middle-overlapped helical baffles and segmental baffles[J]. Chemical Engineering Science, 2009, 64(8): 1643-1653. DOI:10.1016/j.ces.2008.12.018 |
| [20] |
LEI Y G, HE Y L, CHU P, et al. Design and optimization of heat exchangers with helical baffles[J]. Chemical Engineering Science, 2008, 63(17): 4386-4395. DOI:10.1016/j.ces.2008.05.044 |
| [21] |
王斯民, 王萌萌, 顾昕, 等. 基于火积理论的螺旋折流板换热器结构优化[J]. 高校化学工程学报, 2016, 30(3): 532-539. WANG S M, WANG M M, GU X, et al. Structure optimization of helical baffle heat exchangers using entransy theory[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(3): 532-539. DOI:10.3969/j.issn.1003-9015.2016.03.005 |
| [22] |
RIOS-IRIBE E Y, CERVANTES-GAXIOLA M E, RUBIO-CASTRO E, et al. Heat transfer analysis of a non-Newtonian fluid flowing through a plate heat exchanger using CFD[J]. Applied Thermal Engineering, 2015, 84(6): 225-236. |
| [23] |
HUGHES W F, BRIGHTON J A. Schaum's outline of theory and problems of fluid dynamics[M]. New York: McGraw-Hill, 1967.
|
| [24] |
岑可法, 姚强, 曹欣玉, 等. 煤浆燃烧、流动、传热和气化的理论与应用技术[M]. 杭州: 浙江大学出版社, 1997. CEN K F, YAO Q, CAO X Y, et al. Theoru and application of combustion, flow, heat transfer, gasfication of coal slurry[M]. Hangzhou: Zhejiang University press, 1997. |
| [25] |
赵碧, 蔡京荣. 水煤浆加压气化技术工艺特点及应用[J]. 氮肥技术, 2017, 38(5): 8-12. ZHAO B, CAI J R. Characteristics and application of the technology of coal-water slurry pressurized gasification[J]. DANFEI JISHU, 2017, 38(5): 8-12. |
| [26] |
王斯民, 王萌萌, 顾昕, 等. 螺旋折流板换热器结构参数多目标优化的数值模拟[J]. 西安交通大学学报, 2015, 49(11): 14-19, 109. WANG S M, WANG M M, GU X, et al. Multi-objective optimization on the structural parameters of shell-and-tube heat exchanger with helical baffles[J]. Journal of Xi'an Jiaotong University, 2015, 49(11): 14-19, 109. |




