2. 西安交通大学 能源与动力工程学院,陕西 西安 710049
2. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
缠绕管式换热器属于一种管壳式换热器,其换热管束以螺旋缠绕的形式排列在壳体内部,具有结构紧凑、耐高压、热应力小、换热系数高、流体适应性强、可实现多种介质同时换热等优点,广泛应用于制药、食品、石油、化工、冶金、电力和纺织等行业[1-3]。很多学者对圆形光管缠绕管换热器进行了研究。LU等[4-5]实验研究并模拟了恒定功率电加热条件下壳侧空气流动及换热。NEERAAS等[6-7]对多种实验工质单相换热和两相混合换热进行了实验研究,拟合了努塞尔数Nu和摩擦系数f的经验关联式。ZENG等[8]模拟了多层缠绕管换热器壳侧流动和换热,使用田口算法评估了主要结构参数的影响,得出了Nu和f的多参数关联式;TANG等[9]实验并模拟了四层缠绕管换热器壳侧空气流动和换热,实验结果与Messa的压降关联式偏差12.82%。REN等[10-11]模拟了左右晃动或旋转搅动状态下,壳侧液化天然气流动和换热,模拟与实验结果的压降偏差为16.81%。FERNG等[12]研究了一根缠绕管的换热器,分析了迪恩Dean数和管间距的影响,与实验结果吻合良好。王斯民等[13]模拟分析了关键几何参数的影响,使用多目标遗传算法优化了结构。WANG等[14]模拟发现交错分布的垫条能够增加流体扰动、增强换热;垫条数量的影响不大。以上研究为异形管缠绕管换热器的研究奠定了基础。RAINIERI等[15]实验研究了螺纹管和光滑管绕管曲率和螺纹结构的影响,结果表明低Dean数下,绕管曲率的影响占优;在高Dean数下,螺纹结构占优。NAPHON[16]对绕管外带翅片和不带翅片的缠绕管换热器进行了实验研究。GUPTA等[17]实验研究了外翅片管(管内有波纹)不同于光管的压降关联式。尹接喜等[18]模拟了并管结构缠绕管换热器。马飞[19]建立了椭圆管和三叶管的缠绕管换热器模型,结果表明三叶管的综合性能最好。田杨等[20]模拟发现与圆形管缠绕管换热器相比,水滴形管能大幅度降低壳侧压降。
异形管缠绕管换热器的数值模拟研究集中在改变圆管截面大尺寸方面,例如:三叶管、椭圆管,对改变圆管截面微小尺寸进而强化换热的研究鲜有报道。本文基于流动传热强化机理,提出了基于开槽强化管的缠绕管换热器,使用Fluent 18.0数值分析了壳侧空气流动、换热和综合性能随凹槽数量和深度的变化规律,并与圆形光管缠绕管式换热器进行了对比。
2 计算模型及数值方法 2.1 几何模型的建立本文建立了缠绕管式换热器的三维模型,其主要结构参数如图 1所示,芯桶的外部直径

|
图 1 缠绕管换热器的几何结构 Fig.1 Geometric structure of spiral-wound heat exchangers |

|
图 2 开槽缠绕管截面图 Fig.2 Cross-section diagram of grooved spiral-wound tubes |
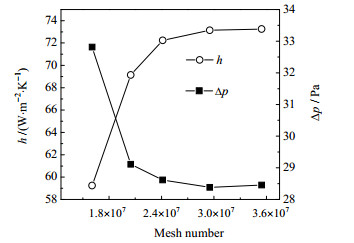
由于管外壁凹槽深度很小,将凹槽部分独立划出后进行网格划分。凹槽内的计算域采用结构化网格,其余部分采用非结构化网格划分,如图 3所示。对凹槽数量为2,凹槽深度为0.3 mm几何模型的网格进行了独立性验证,网格数量为16 056 225 ~ 35 456 358,结果如图 4所示。当网格数量大于24 133 963时,对流换热系数h的变化小于1.5 %,压降Δp的变化小于1.0 %。所以取网格数量29 512 101满足要求。不同组合下计算域的网格单元数为2 500万~3 600万。

|
图 3 凹槽内网格细节图 Fig.3 Detailed profile of mesh in grooves |
|
图 4 网格独立性验证 Fig.4 Validation of mesh independence |
本文的计算工质为空气,在换热器壳侧单相换热,物性不变。入口边界条件是速度入口,为3.0、3.5、4.0、4.5和5.0 m·s-1,空气进口温度为300 K,出口边界条件为压力出口;换热管壁温恒定,为330 K,其余壁面均为无滑移绝热壁面;壁面函数为默认的标准壁面函数,压力和速度耦合采用SIMPLE算法,动量和能量方程均为二阶迎风格式,各项残差小于为1×10-6时,认为收敛。选择RNG k-
连续性方程:
| $\nabla \mathit{\boldsymbol{u}} = 0$ | (1) |
动量守恒方程
| $\nabla (\rho u\mathit{\boldsymbol{u}}) = \frac{\partial }{{\partial x}}(\eta \frac{{\partial u}}{{\partial x}}) + \frac{\partial }{{\partial y}}(\eta \frac{{\partial u}}{{\partial y}}) + \frac{\partial }{{\partial z}}(\eta \frac{{\partial u}}{{\partial z}}) - \frac{{\partial p}}{{\partial x}}$ | (2) |
| $\nabla (\rho v\mathit{\boldsymbol{u}}) = \frac{\partial }{{\partial x}}(\eta \frac{{\partial v}}{{\partial x}}) + \frac{\partial }{{\partial y}}(\eta \frac{{\partial v}}{{\partial y}}) + \frac{\partial }{{\partial z}}(\eta \frac{{\partial v}}{{\partial z}}) - \frac{{\partial p}}{{\partial y}}$ | (3) |
| $\nabla (\rho w\mathit{\boldsymbol{u}}) = \frac{\partial }{{\partial x}}(\eta \frac{{\partial w}}{{\partial x}}) + \frac{\partial }{{\partial y}}(\eta \frac{{\partial w}}{{\partial y}}) + \frac{\partial }{{\partial z}}(\eta \frac{{\partial w}}{{\partial z}}) - \frac{{\partial p}}{{\partial {\rm{z}}}}$ | (4) |
能量守恒方程
| $\nabla (\rho \mathit{\boldsymbol{u}}T) = \frac{\partial }{{\partial x}}\left( {\frac{\lambda }{{{c_p}}}\frac{{\partial T}}{{\partial x}}} \right){\rm{ + }}\frac{\partial }{{\partial y}}\left( {\frac{\lambda }{{{c_p}}}\frac{{\partial T}}{{\partial y}}} \right){\rm{ + }}\frac{\partial }{{\partial z}}\left( {\frac{\lambda }{{{c_p}}}\frac{{\partial T}}{{\partial z}}} \right){\rm{ + }}{S_T}$ | (5) |
湍动能k方程
| $\frac{\partial }{{\partial t}}\left( {\rho k} \right) + \nabla \left( {\rho k\mathit{\boldsymbol{u}}} \right) = \frac{\partial }{{\partial x}}\left[ {\left( {{\alpha _k}{\eta _{{\rm{eff}}}}} \right)\frac{{\partial k}}{{\partial x}}} \right] + \frac{\partial }{{\partial y}}\left[ {\left( {{\alpha _k}{\eta _{{\rm{eff}}}}} \right)\frac{{\partial k}}{{\partial y}}} \right] + \frac{\partial }{{\partial z}}\left[ {\left( {{\alpha _k}{\eta _{{\rm{eff}}}}} \right)\frac{{\partial k}}{{\partial z}}} \right] + {G_k} - \rho \varepsilon $ | (6) |
湍动能耗散
| $\frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \nabla \left( {\rho \varepsilon \mathit{\boldsymbol{u}}} \right) = \frac{\partial }{{\partial x}}\left[ {\left( {{\alpha _{_\varepsilon }}{\eta _{{\rm{eff}}}}} \right)\frac{{\partial \varepsilon }}{{\partial x}}} \right] + \frac{\partial }{{\partial y}}\left[ {\left( {{\alpha _{_\varepsilon }}{\eta _{{\rm{eff}}}}} \right)\frac{{\partial \varepsilon }}{{\partial y}}} \right] + \frac{\partial }{{\partial z}}\left[ {\left( {{\alpha _{_\varepsilon }}{\eta _{{\rm{eff}}}}} \right)\frac{{\partial \varepsilon }}{{\partial z}}} \right] + C_{1\varepsilon }^*\frac{\varepsilon }{k}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}$ | (7) |
式中:u为速度的矢量形式,m·s-1;u、v、w分别为x、y、z方向的速度,m·s-1;cp为流体的定压比热容,J·kg-1·K-1;p为压力,Pa;T为温度,K;ρ为流体的密度,kg·m-3;λ为流体的导热系数,W·m-1·K-1;ST为能量方程的广义源项;Gk为平均速度梯度引起的湍动能产生项;η为流体的动力黏度,Pa·s;ηtur为流体的湍动黏度,Pa·s;ηeff为流体的有效黏度,Pa·s;
基于计算流体动力学(computational fluid dynamics,CFD)原理[21],可得到流体域范围内的速度,温度和压力。h和Δp可使用CFD-Post 18.0软件按式(8)和(9)处理:
| $h = \frac{{{c_p}\dot m({T_{{\rm{outlet}}}} - {T_{{\rm{inlet}}}})}}{A}$ | (8) |
式中:
| $\Delta p = {p_{{\rm{inlet}}}} - {p_{{\rm{outlet}}}}$ | (9) |
式中:pinlet和poutlet分别为进出口平均压力,Pa。
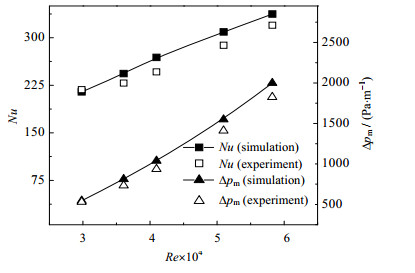
2.3 模型的验证将数值计算得到的Nu和单位长度压降Δpm与文献[7]中实验所得的数据进行对比,如图 5所示。工质为甲烷气体。努塞尔数Nu和单位长度压降的平均偏差分别为5.67 %和7.90 %。换热管壁外其余壁面绝热导致模拟的Nu偏高;气体物性不变的假设,忽略了气体被加热时密度减小,导致模拟得出的压降值偏高。
|
图 5 实验与模拟结果对比 Fig.5 Comparison of experiment and simulation results |
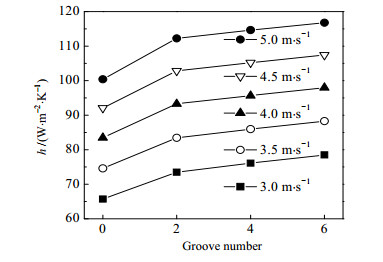
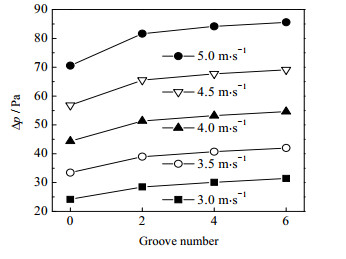
图 6~8分别显示了换热管缠绕角度为9.5°,凹槽深度为0.3 mm时,不同的壳侧入口速度下,h、Δp和换热器综合性能指标(performance evaluation criteria,PEC=Nu·f1/3)随凹槽数量的变化。如图 6和7所示,随着凹槽数量的增加,h和Δp都有所增加,且增加趋势逐渐变缓。以壳侧入口速度3 m·s-1为例,当凹槽数量为2时,h比圆形光管增大了11.86 %,Δp增大了17.75 %;当凹槽数量为6时,与圆形光管相比h增大了19.46 %,Δp增大了29.86 %。其余速度条件下,增加效果相当。这是因为凹槽开在传热管的两侧,凹槽的切线方向与流动方向接近垂直,增加了流体扰动,能够破坏沿流动方向发展的边界层,使热量通过涡流扩散的方式得到有效的传递,从而增大了对流换热系数。同时,流体扰动增强,湍动能增大,流体的内摩擦力变大,分子之间的碰撞更剧烈,造成了更大的能量损失,因此压降增大。
|
图 6 不同壳侧入口速度条件下对流换热系数h随凹槽数量的变化 Fig.6 Profiles of heat transfer coefficient h as a function of groove number under different inlet-velocities in shell side |
|
图 7 不同壳侧入口速度条件下压降Δp随凹槽数量的变化 Fig.7 Profiles of pressure drop Δp as a function of groove number under different inlet-velocities in shell side |
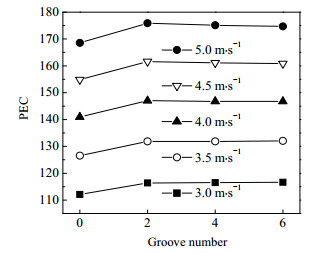
|
图 8 不同壳侧入口速度条件下综合评价指标PEC随凹槽数量的变化 Fig.8 Profiles of comprehensive evalution index PEC as a function of groove number under different inlet-velocities in shell side |
采用PEC来比较圆形管与凹槽管形的缠绕管式器壳侧的流动和换热性能,综合考虑了压降和换热,解决了换热增强和压降损失增大之间的矛盾,合理给定了两者之间的比重,能够评价换热器的综合性能。如图 8所示,随凹槽数量的增加,PEC在有2个凹槽时,比圆形光管先是有明显提高,再增加凹槽数量,PEC保持基本不变,即换热器的综合性能与凹槽数量无关,2个凹槽数量就可达到与更多凹槽数量一样的增强效果。以速度为3 m·s-1为例,凹槽数量为2的情况下,PEC相对圆形光管增加了3.82%。在不同速度工况下,2个凹槽的缠绕管换热器相对圆形光管PEC增加率平均为4.21 %。这是由于凹槽数量增多时,对流换热系数得到增强的同时,压降也增大了,综合考虑两方面因素,性能并没有得到进一步提高。
3.2 凹槽深度对流动和换热的影响如图 9所示,显示了凹槽数量为2,缠绕角度为9.5°时,h随凹槽深度在不同壳侧入口速度下的变化。从图 9可以看出,h随凹槽深度的增加先增大后减小,峰值在凹槽深度为0.3 mm时取得。在凹槽深度为0.3 mm时,在不同速度工况下,h比圆形光管的平均增长了11.79 %。这是因为,随凹槽深度增大,一方面流体扰动增强,流体的湍动能增大,流体分子剧烈碰撞,热量通过涡旋扩散的方式快速传递,对流换热系数增大,另一方面,在凹槽过深时,会引起流体在凹槽内部的滞流,热量通过一部分导热的方式来传递,形成了热阻,传热恶化。在凹槽深度较浅时,流体扰动占主导,换热增强,在进一步加深凹槽时,流体滞流引起的传热恶化占比越来越大,减小了对流换热系数。
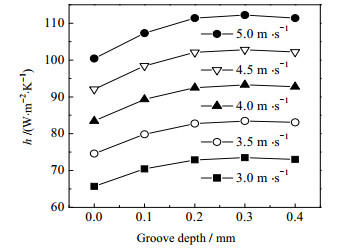
|
图 9 不同壳侧入口速度条件下对流换热系数h随槽深度的变化 Fig.9 Profiles of heat transfer coefficient h as a function of groove depth under different inlet-velocities in shell side |
如图 10显示了凹槽数量为2,缠绕角度为9.5°时,Δp随凹槽深度在不同壳侧入口速度下的变化。由图可以看出,Δp随凹槽深度先增大后维持不变,因为在凹槽深度为0.2、0.3 mm和0.4 mm情况下,Δp的偏差为0.05 %~1.41%,认为相等。不同速度工况下,凹槽深度为0.2 mm时,Δp比圆形光管平均增长了16.61%。由于当槽深度过大时,流体在凹槽内滞流后,流体在流经凹槽时,并没有得到更剧烈的扰动,湍动能的提高微弱。
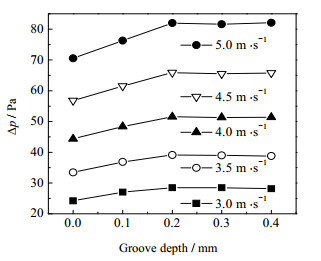
|
图 10 不同壳侧入口速度条件下压降Δp随凹槽深度的变化 Fig.10 Profiles of pressure drop Δp as a function of groove depth under different inlet-velocities in shell side |
PEC随凹槽深度的变化如图 11所示,可以看出,PEC随凹槽深度的增大先增大后减少,存在峰值,在凹槽深度为0.3 mm时取得。凹槽深度为0.3 mm时,不同速度工况下,相对圆形光管PEC增加率平均为4.21 %。值得注意的是,凹槽深度为0.4 mm时的增强效果不及0.1 mm时的增强效果,可见凹槽深度并不是越大越好。随凹槽深度增大,流体滞流在凹槽内部,使得换热恶化,压降损失维持不变,因此,缠绕管式换热器的综合性能变差。
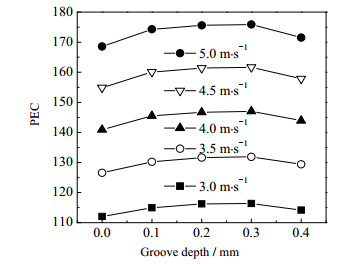
|
图 11 不同壳侧入口速度条件下综合评价指标PEC随凹槽深度的变化 Fig.11 Profiles of comprehensive evalution index PEC as a function of groove depth under different inlet-velocities in shell side |
本文建立了基于开槽强化管的的缠绕管式换热器的三维模型,在圆形光滑缠绕管两侧沿管中心线开了不同数量和不同深度的半圆形凹槽,采用数值模拟的方法研究该种换热器壳侧空气流动、换热和综合性能随凹槽数量和凹槽深度的变化规律,与圆形光管缠绕管式换热器进行了对比。得出了以下结论:
(1) 与圆形传热管相比,凹槽的存在切断了边界层,增加了扰动,增强换热,换热器的综合性能有所提升。
(2) 当流体入口速度一定时,凹槽数量的增多,一方面增强了换热,另一方面增加了阻力压降;从换热器的综合性能来看,PEC并不随凹槽数量的增大而增大,而是维持基本不变,但相比圆形光管增强了约4.21 %。
(3) 对于凹槽深度的影响,当流体的入口流速一定时,对流换热系数和压降都随凹槽深度的增大先增大后减小,PEC在凹槽深度0.3 mm时取得最优值,此值与圆形光管相比,提高了约4.21 %。
| [1] |
肖娟, 简冠平, 王家瑞. 缠管式换热器性能及应用研究进展[J]. 化工机械, 2016, 43(4): 423-428. XIAO J, JIAN G P, WANG J R, et al. Progress in performance and application study for wound-tube heat exchanger[J]. Chemical Engineering & Machinery, 2016, 43(4): 423-428. DOI:10.3969/j.issn.0254-6094.2016.04.001 |
| [2] |
PACIO J C, DORAO C A. A review on heat exchanger thermal hydraulic models for cryogenic applications[J]. Cryogenics, 2011, 51(7): 366-379. DOI:10.1016/j.cryogenics.2011.04.005 |
| [3] |
TANG Q X, CHEN G F, YANG Z Q, et al. Numerical investigation on gas flow heat transfer and pressure drop in the shell side of spiral-wound heat exchangers[J]. Science China (Technological Sciences), 2018, 61(4): 506-515. DOI:10.1007/s11431-017-9176-9 |
| [4] |
LU X, DU X, ZENG M, et al. Shell-side thermal-hydraulic performances of multilayer spiral-wound heat exchangers under different wall thermal boundary conditions[J]. Applied Thermal Engineering, 2014, 70(2): 1216-1227. DOI:10.1016/j.applthermaleng.2014.02.053 |
| [5] |
LU X, DU X P, ZHANG S. Experimental and numerical investigation on shell-side performance of multilayer spiral-wound heat exchangers[J]. Chemical Engineering Transactions, 2013, 35: 445-450. |
| [6] |
NEERAAS B O, FREDHEIM A O, AUNAN B. Experimental shell-side heat transfer and pressure drop in gas flow for spiral-wound LNG heat exchanger[J]. International Journal of Heat and Mass Transfer, 2004, 47(2): 353-361. DOI:10.1016/S0017-9310(03)00400-9 |
| [7] |
NEERAAS B O, FREDHEIM A O, AUNAN B. Experimental data and model for heat transfer, in liquid falling film flow on shell-side, for spiral-wound LNG heat exchanger[J]. International Journal of Heat and Mass Transfer, 2004, 47(14/15/16): 3565-3572. |
| [8] |
ZENG M, ZHANG G, LI Y, et al. Geometrical parametric analysis of flow and heat transfer in the shell side of a spiral-wound heat exchanger[J]. Heat Transfer Engineering, 2015, 36(9): 790-805. DOI:10.1080/01457632.2015.963386 |
| [9] |
TANG Q X, CHEN G F, GUO H, et al. Experimental and numerical investigation on gas flow in shell side of spiral-wound heat exchangers[J]. Cryogenics, 2017, 5: 1-5, 11. |
| [10] |
REN Y, CAI W H, JIANG Y Q. Numerical study on shell-side flow and heat transfer of spiral-wound heat exchanger under sloshing working conditions[J]. Applied Thermal Engineering, 2018, 134: 287-297. DOI:10.1016/j.applthermaleng.2018.01.119 |
| [11] |
REN Y, CAI W H, CHEN J, et al. Numerical study on the shell-side flow and heat transfer of superheated vapor flow in spiral wound heat exchanger under rolling working conditions[J]. International Journal of Heat and Mass Transfer, 2018, 121: 691-702. DOI:10.1016/j.ijheatmasstransfer.2018.01.025 |
| [12] |
FERNG Y M, LIN W C, CHIENG C C. Numerically investigated effects of different Dean number and pitch size on flow and heat transfer characteristics in a helically coil-tube heat exchanger[J]. Applied Thermal Engineering, 2012, 36: 378-385. DOI:10.1016/j.applthermaleng.2011.10.052 |
| [13] |
王斯民, 简冠平, 肖娟, 等. 缠绕管式换热器结构参数多目标优化数值模拟研究[J]. 西安交通大学学报, 2017, 51(5): 9-15. WANG S M, JIAN G P, XIAO J, et al. Multi-objective optimization on the structural parameters of spiral wound heat exchanger[J]. Journal of Xi'an Jiaotong University, 2017, 51(5): 9-15. |
| [14] |
WANG S M, JIAN G P, TONG X, et al. Effects of spacing bars on the performance of spiral-wound heat exchanger and the fitting of empirical correlations[J]. Applied Thermal Engineering, 2018, 128: 1351-1358. DOI:10.1016/j.applthermaleng.2017.09.094 |
| [15] |
RAINIERI S, ZOZZOLI F, CATTANI L, et al. Compound convective heat transfer enhancement in helically coiled wall corrugated tubes[J]. International Journal of Heat and Mass Transfer, 2013, 59: 353-362. DOI:10.1016/j.ijheatmasstransfer.2012.12.037 |
| [16] |
NAPHON P. Thermal performance and pressure drop of the helical-coil heat exchangers with and without helically crimped fins[J]. International Communications in Heat and Mass Transfer, 2007, 34(3): 321-330. DOI:10.1016/j.icheatmasstransfer.2006.11.009 |
| [17] |
GUPTA P K, KUSH P K, TIWARI A. Experimental studies on pressure drop characteristics of cryogenic cross-counter flow coiled finned tube heat exchangers[J]. Cryogenics, 2010, 50(4): 257-265. DOI:10.1016/j.cryogenics.2010.01.012 |
| [18] |
尹接喜, 李清海, 施德强, 等. 缠绕管换热器并管传热模型及实验[J]. 清华大学学报(自然科学版), 2000(6): 73-75, 79. YIN J X, LI Q H, SHI D Q, et al. Heat transfer model land experiment for paired-tubes wound-tube heat exchangers[J]. Journal of Tsinghua University (Science and Technology), 2000(6): 73-75, 79. DOI:10.3321/j.issn:1000-0054.2000.06.021 |
| [19] |
马飞.缠绕管换热器传热数值模拟[D].郑州: 郑州大学, 2014. MA F. Numerical simulation of heat transfer of spiral coiled heat exchanger[D]. Zhengzhou: Zhengzhou University, 2014. |
| [20] |
田杨, 陈光辉, 李建隆. 水滴型缠绕管换热器壳程流动与传热研究[J]. 化工设计通讯, 2017, 43(7): 147-149, 151. TIAN Y, CHEN G H, LI J L. Study on flow and heat transfer of shell-side coil-wound heat exchanger in water drop type[J]. Chemical Engineering Design Communications, 2017, 43(07): 147-149, 151. DOI:10.3969/j.issn.1003-6490.2017.07.137 |
| [21] |
王福军. 计算流体动力学分析——CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. WANG F J. Computational fluid dynamics analysis-theory and application of CFD software[M]. Beijing: Tsinghua University Press, 2004. |




