2. 江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122
2. Key Laboratory of Advanced Process Control for Light Industry(Ministry Of Education), Jiangnan University, Wuxi 214122, China
随着现代化工过程生产规模的不断扩大,工艺流程复杂程度也越来越高,故障监测已成为化工过程控制领域的研究热点。多元统计过程监控方法(multivariate statistical process monitoring,MSPM)已广泛应用于过程监控领域[1-3],其中主元分析法(principal component analysis,PCA)是多元统计方法中最常用的方法。
传统挑选主元个数的方法有累积方差贡献率法[4] (cumulative percent variance,CPV)、重构误差方差法[5]和故障信噪比法[6]等。其中CPV方法主要保留了方差变化最大的主元,使其达到预先设定的比例(一般为85%),这样可以认为数据的绝大部分信息都被包含在主元模型中,但该方法中比例值的确定没有较客观的方法。重构误差方差法是基于重构误差来选择主元,当重构误差最小时,选取最优主元个数。以上两种方法均是基于方差最大化对主元进行排序,并从降维角度选择最优主元个数,而故障信噪比方法考虑了故障对主元个数的影响,在故障信噪比最大时选择最优主元个数。
在故障监测领域,主元个数的选取对监测性能同样有着十分重要的影响。王海清等[7]综合考虑了主元个数对不同故障的检测要求,提出采用最优临界故障幅值来确定主元个数,提高对故障的监测能力;TAMURA等[6]利用先验故障信息,确定故障信噪比与主元个数之间的关系,选择当传感器故障具有最大灵敏度时的主元个数;XUAN等[8]在故障信噪比的基础上,提出了最小可检测故障幅度的概念,并据此定义了一种可检测故障覆盖范围的性能指标,当可检测故障覆盖率最大时的主元个数为最优主元个数;PRIETO等[9]利用判别分析(discriminant analysis, DA)选择主元,最大限度地提高了类与类之间的可分离性,以达到更优的故障诊断效果。
上述方法通过定义某种指标,建立故障监测效果与主元个数之间的关系来选取最优的主元个数,以提高故障的监测精度。但是,方差变化较大的主元并不一定包含更多的故障信息,若只是单纯地将方差大的主元放在一个子空间内监测,可能会损失重要的故障信息,因此只对主元个数作优化存在一定的局限性。陶阳等[10]通过Relief算法提取对故障更相关的主元进行监测,避免了传统PCA算法在主元挑选中的盲目性与主观性;ZHAO等[11]提出故障相关主成分分析算法(fault-relevant principal component analysis, FPCA),利用故障数据信息进一步将主元子空间和残差子空间划分为故障相关子空间与故障不相关子空间共4个子空间进行监测;仓文涛等[12]提出Informative-PCA方法,通过构造累积T2统计量的变化率,衡量过程信息在各主元上的富集程度,认为变化率更大的主元方向在故障检测中更重要,由此提取故障相关主元。JIANG等[13]提出敏感主元分析(sensitive principal component analysis, SPCA)的故障监测算法,通过实时监测T2统计量的变化率,选择在当前时刻变化率最大的若干主元进行监测。其中前两种方法建模时均需要故障数据集的支撑,而后两种方法则通过观察T2统计量在各个方向上的变化率来挑选主元。
综上所述,在PCA故障监测模型中,主元的选取至关重要,由于方差变化较大的主元并不一定包含更多的故障信息,因此本文通过对T2统计量进行分析,定义一种故障敏感程度系数ε作为主元排序准则,选择出每个变量方向上发生故障时最敏感的主元;然后基于多块监测的思想,并行计算多个PCA模型,覆盖所有的变量方向,从而无论故障发生在哪个方向上,均有相应的子块对其进行有效监测。该方法一方面可以无需借助故障数据集提取主元,另一方面避免了实时建模耗费的计算资源。最后通过一个数值例子以及田纳西伊斯曼(Tennessee Eastman, TE)过程的仿真实验与实际高炉炼铁过程应用验证了所提方法的有效性与监测性能。
2 传统PCA监控方法传统PCA以变量间方差最大化为准则提取主元,假设标准化后的正常工况数据集为
| $ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{P}}^{\rm{T}}} + \mathit{\boldsymbol{E}} $ | (1) |
其中载荷矩阵P可由协方差矩阵C作特征值分解得到
| $ \mathit{\boldsymbol{C}} = \frac{1}{{n - 1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{V \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{V}}^{\rm{T}}} $ | (2) |
主元载荷矩阵P即为特征值矩阵V的前k列,Λ为特征值从小到大排列的对角阵,特征值的大小同时反映了数据方差的大小。PCA方法通过构造T2与SPE两个统计量进行故障监测
| $ {T^2} = \mathit{\boldsymbol{x}}_{{\rm{test}}}^{\rm{T}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{x}}_{{\rm{test}}}} \le T_{{\rm{lim}}}^2 $ | (3) |
| $ {\rm{SPE}} = \mathit{\boldsymbol{x}}_{{\rm{test}}}^{\rm{T}}(\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{P}}^{\rm{T}}}){\mathit{\boldsymbol{x}}_{{\rm{test}}}} \le {\rm{SP}}{{\rm{E}}_{{\rm{lim}}}} $ | (4) |
其中
| $ \begin{array}{l} T_{\lim }^2 = \frac{{k(n - 1)}}{{n - k}}{F_{k,(n - k),{\rm{\alpha }}}}\\ SP{E_{\lim }} = {\theta _1}{\left[ {1 + \frac{{{c_{\rm{\alpha }}}\sqrt {2{\theta _2}h_0^2} }}{{{\theta _1}}} + \frac{{{\theta _2}{h_0}({h_0} - 1)}}{{\theta _1^2}}} \right]^{1/{h_0}}} \end{array} $ | (5) |
其中
传统方法将主元按照方差贡献率大小进行排序,但是方差贡献率大的主元并不一定包含了更多的故障信息,同时忽略掉那些方差贡献率小的主元可能会损失重要的故障信息,JOLLIFFE[14]指出方差贡献率小的主元同样十分重要,WANG等[15]证明了故障无关主元会降低故障监测的效果,因此如何选取对故障较为敏感的主元并将它们放在一个空间中进行监测变得尤为重要。
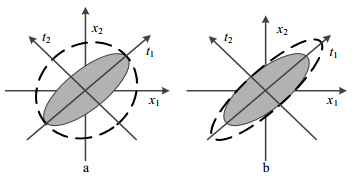
图 1展示了主元选择对不同故障类型监测的影响。其中x1、x2代表过程变量,实心椭圆代表正常工况数据分布,t1、t2代表主元,很明显t1是方差变化更大的主元方向,虚线椭圆是故障数据分布范围,a、b分别代表了两种故障类型。可以看出图 1(a)中故障发生时主元t1对故障监测基本没有任何贡献,而方差变化更小的主元t2反而对故障监测起着十分重要的作用;同时当故障呈现图 1(b)中的分布时,t1主元在监测中起到了最重要的作用。
|
图 1 故障分布对统计监测的影响 Fig.1 Effects of fault distribution on process monitoring |
假设当故障发生在xj上时,即故障样本xf = x+ f,且f除了第j维之外的项均为0,则有第i个主元在故障工况下的T2统计量为
| $ \begin{array}{l} T_{\rm{f}}^2 = \frac{1}{{{\lambda _i}}}{(\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{f}})^{\rm{T}}}{\mathit{\boldsymbol{p}}_i}\mathit{\boldsymbol{p}}_i^{\rm{T}}(\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{f}}) = \frac{1}{{{\lambda _i}}}{\rm{tr}}(\mathit{\boldsymbol{p}}_i^{\rm{T}}(\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{f}}){(\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{f}})^{\rm{T}}}{\mathit{\boldsymbol{p}}_i})\\ = \frac{1}{{{\lambda _i}}}({\rm{tr}}(\mathit{\boldsymbol{p}}_i^{\rm{T}}\mathit{\boldsymbol{x}}{\mathit{\boldsymbol{x}}^{\rm{T}}}{\mathit{\boldsymbol{p}}_i}) + 2{f_j}{p_{ij}}{t_i} + p_{ij}^2f_j^2) = \frac{{t_i^2}}{{{\lambda _i}}} + \frac{{2{f_j}{p_{ij}}{t_i}}}{{{\lambda _i}}} + \frac{{p_{ij}^2f_j^2}}{{{\lambda _i}}} \end{array} $ | (6) |
又有
| $ {t_i} = {p_{i1}}{x_1} + {p_{i2}}{x_2} + \cdots + {p_{im}}{x_m} = \mathit{\boldsymbol{p}}_i^{\rm{T}}\mathit{\boldsymbol{x}} = \mathit{\boldsymbol{p}}_i^{\rm{T}}\mathit{\boldsymbol{V \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{u}}^{\rm{T}}} = {\sigma _i}{u_i} $ | (7) |
其中
| $ (n - 1){\lambda _i} = \sigma _i^2 $ | (8) |
所以有
| $ T_{\text{f}}^{2}=(n-1)(u_{i}^{2}+\frac{2{{f}_{j}}{{p}_{ij}}{{u}_{i}}}{{{\sigma }_{i}}}+\frac{p_{ij}^{2}f_{j}^{2}}{\sigma _{i}^{2}})=(n-1){{({{u}_{i}}+\frac{{{p}_{ij}}{{f}_{j}}}{{{\sigma }_{i}}})}^{2}} $ | (9) |
由式(9)可以看出,选择|pij|/σi更大方向上的主元进行故障监测时,故障样本在这些主元方向上对T2统计量的贡献率更高,对故障也更加敏感。定义一个敏感系数εij,表示第i个主元对第j维变量上故障的敏感程度:
| $ {\varepsilon _{ij}} = \frac{{\left| {{p_{ij}}} \right|}}{{{\sigma _i}}} $ | (10) |
同时定义选择主元敏感程度的阈值为εlim,为了保证每个子块中选择的主元个数不小于1,取其值为各变量上敏感程度最大的主元中的最小值的ω倍,且ω不大于1:
| $ {\varepsilon _{{\rm{lim}}}} = \omega \mathop {{\rm{min}}}\limits_i (\mathop {{\rm{max}}}\limits_j ({\varepsilon _{ij}})) $ | (11) |
通过以上分析,基于新定义的主元敏感度可以挑选出对每一维变量上发生故障最敏感的主元,但实际情况下无法预知故障发生在哪一维或几维上,因此针对每一维变量上可能发生的故障均建立敏感模型,每个模型中包含了对各自变量最敏感的主元,然后将测试样本放入m个子块模型并行监测。假设利用敏感度εij对主元重新排序得到
| $ T_{j, \text{new}}^2 = \sum\limits_{i = 1}^{{k_j}} {\frac{{\mathit{\boldsymbol{x}}_{{\rm{test}}}^{\rm{T}}\mathit{\boldsymbol{p}}_i^j\mathit{\boldsymbol{p}}_i^{j{\rm{T}}}{\mathit{\boldsymbol{x}}_{{\rm{test}}}}}}{{\lambda _i^j}}} $ | (12) |
其中kj为第j个子块中选取的主元个数,
| $ T_{j,{\rm{lim}}}^2 = \frac{{{k_j}(n - 1)}}{{n - {k_j}}}{F_{{k_j},(n - {k_j}),{\rm{α}}}} $ | (13) |
依次计算出每个子块的统计量与控制限,然后利用贝叶斯信息准则方法(Bayesian information criterion, BIC)[16]对子块监测结果进行融合,在贝叶斯信息准则方法中,测试样本xtest在第j个子块中T2统计量的故障条件概率可表示为:
| $ {P_{{{\rm{T}}^{\rm{2}}}}}(F|{\mathit{\boldsymbol{x}}_{{\rm{test}}, j}}) = \frac{{{P_{{{\rm{T}}^{\rm{2}}}}}({\mathit{\boldsymbol{x}}_{{\rm{test}}, j}}|F){P_{{{\rm{T}}^{\rm{2}}}}}(F)}}{{{P_{{{\rm{T}}^{\rm{2}}}}}({\mathit{\boldsymbol{x}}_{{\rm{test}}, j}})}} $ | (14) |
| $ {P_{{{\rm{T}}^{\rm{2}}}}}({\mathit{\boldsymbol{x}}_{{\rm{test}}, j}}) = {P_{{{\rm{T}}^{\rm{2}}}}}({\mathit{\boldsymbol{x}}_{{\rm{test}}, j}}|N){P_{{{\rm{T}}^{\rm{2}}}}}(N) + {P_{{{\rm{T}}^{\rm{2}}}}}({\mathit{\boldsymbol{x}}_{{\rm{test}}, j}}|N){P_{{{\rm{T}}^{\rm{2}}}}}(F) $ | (15) |
其中xtest, j表示第j个子块中的测试样本,在本文中每个子块的测试样本均相同,似然函数
| $ {P_{{{\rm{T}}^{\rm{2}}}}}({\mathit{\boldsymbol{x}}_{{\rm{test}}, j}}|N) = {e^{ - T_{j, {\rm{new}}}^2/T_{j, {\rm{lim}}}^{\rm{2}}}} , {P_{{{\rm{T}}^{\rm{2}}}}}({\mathit{\boldsymbol{x}}_{{\rm{test}}, i}}|F) = {e^{ - T_{j, {\rm{lim}}}^{\rm{2}}/T_{j, {\rm{new}}}^2}} $ | (16) |
其中符号“N”和“F”分别代表正常和故障的情况,PT2(N)是正常样本的先验概率,其值为置信度β,通常取0.99,则
| $ {\rm{BI}}{{\rm{C}}_{{{\rm{T}}^{\rm{2}}}}} = \sum\limits_{j = 1}^m {\left\{ {\frac{{{P_{{{\rm{T}}^{\rm{2}}}}}({\mathit{\boldsymbol{x}}_{{\rm{test}}, i}}|F){P_{{{\rm{T}}^{\rm{2}}}}}(F|{\mathit{\boldsymbol{x}}_{{\rm{test}}, i}})}}{{\sum\limits_{i = 1}^m {{P_{{{\rm{T}}^{\rm{2}}}}}({\mathit{\boldsymbol{x}}_{{\rm{test}}, i}}|F)} }}} \right\}} $ | (17) |
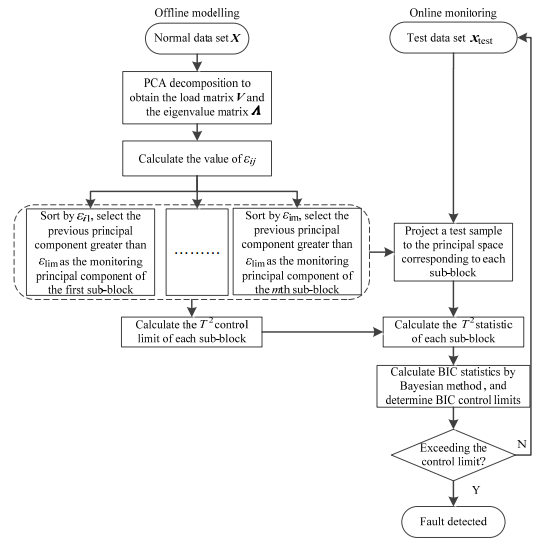
基于故障敏感主元的多块PCA (multi-block PCA process monitoring based on fault sensitive principal component,MBSPCA)的故障监测算法流程如图 2所示,算法流程详细描述如下:
|
图 2 基于MBSPCA故障监测算法流程图 Fig.2 Flow chart based on MBSPCA process monitoring algorithm |
step 1:对正常工况数据集作标准化处理,并利用式(2)进行PCA分解得到载荷矩阵V与特征值矩阵Λ;
step 2:利用式(10)计算εij的值,并以此对载荷向量进行排序得到
step 3:对于新来的测试样本xtest,依次将其放入每个子块模型中通过式(12)计算T2统计量,并与控制限作比较,得到子块监测结果。
step 4:利用贝叶斯方法对所有子块监测结果进行融合,利用式(17)得到BIC统计量监测结果。
step 5:当BIC统计量大于控制限时,则认为监测到故障的发生。
4 仿真实验 4.1 数值仿真采用文献[17]中的数值仿真,其具体结构为:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_1}}\\ {{\mathit{\boldsymbol{x}}_2}}\\ {{\mathit{\boldsymbol{x}}_3}}\\ {{\mathit{\boldsymbol{x}}_4}}\\ {{\mathit{\boldsymbol{x}}_5}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&3&1\\ 3&1&1\\ 4&1&3\\ 4&4&3\\ 1&1&2 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{z_1}}\\ {{z_2}}\\ {{z_3}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{e_1}}\\ {{e_2}}\\ {{e_3}}\\ {{e_4}}\\ {{e_5}} \end{array}} \right] $ |
其中xi (i = 1, 2, …, 5)表示变量,[z1 z2 z3]T表示源变量,ej (j = 1, 2, …, 5)表示噪声,其中:
| $ {z_i} \sim U([0,1])\;(i = 1,2,3),{e_j} \sim N(0,{0.05^2})\;(j = 1,2,3,4,5) $ |
U([0, 1])表示在区间[0, 1]上的均匀分布,N(0, 0.052)表示均值为0,方差为0.052的正态分布。该数值例子中共产生1 000组训练样本,故障设置如下(故障均从第501个样本点开始):
故障1:在x1上加上一个幅值为0.35的阶跃故障;
故障2:在x2上加上一个0.001×(i-400)的斜坡故障。
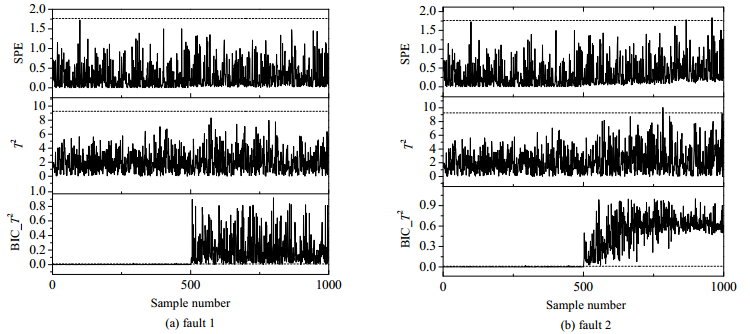
图 3(a)、(b)分别为故障1、2的监测结果,其中前500个样本是正常工况的样本,后500个样本是故障工况的样本,红色实线代表故障控制限,T2与SPE为传统PCA方法的两个统计量,BICT2是基于MBSPCA算法的统计量,可以看出传统PCA方法的监测效果均不理想。结合表 1中结果分析可知,针对故障1,第5主元对其最敏感,但传统PCA方法监测时主元空间中选择了前3个主元(前3个主元累积方差贡献率大于85%),无法监测到故障;同时残差空间中由于第4主元的存在弱化了监测效果,使得SPE统计量也无法监测到故障,故障2中情况与故障1类似。到故障,故障2中情况与故障1类似。
|
图 3 PCA方法与MBSPCA方法对故障1、2监测结果比较 Fig.3 Comparison of PCA and MBSPCA methods for faults 1 and 2 monitoring |
|
|
表 1 各主元对变量的敏感程度 Table 1 Sensitivity of each principal component against different variables |
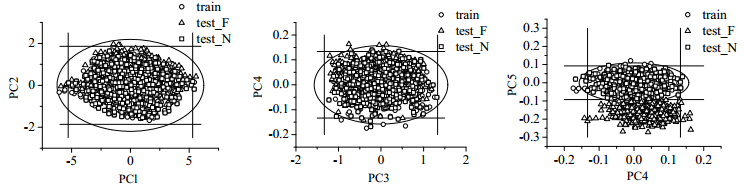
图 4为故障1在各个主元方向上的监测散点图,其中图 4(a)为第1主元(PC1)与第2主元(PC2)的监测散点图,train代表训练样本、test_N代表测试集中的正常样本、test_F代表测试集中的故障样本、黑色直线代表各主元方向上的控制限、椭圆代表两个主元方向的控制限。可以看到前4个主元并不能监测到故障的发生,由此可知故障信息并不一定包含在方差变化大的主元中,事实上由于特征值较大的原因,方差较大的主元对故障的敏感程度ε往往较小。图 4(c)中可以看到PC5方向上明显将故障样本与正常样本分开,可知PC5对故障1的监测更加敏感,与表 1中的结论相符。同时与两个主元同时监测相比,单利用PC5监测时漏报率更低。
|
图 4 故障1在各主元方向上的监测散点图 Fig.4 Monitoring scatter plots of fault 1 in different principal directions |
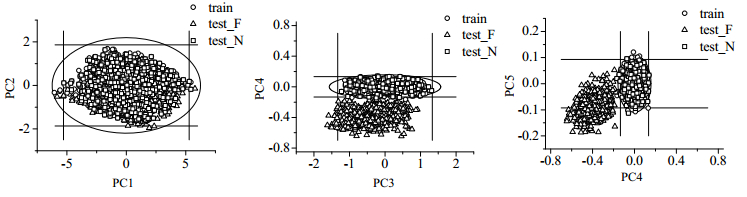
图 5为故障2的监测散点图,可以看到前3个主元对该故障监测效果很差,同时可以发现当随着故障幅值增大时,PC3能监测到小部分故障而PC5能监测到半数故障,这是由于PC5比PC3更加敏感,随着故障幅值的增大,PC5能够先于PC3监测到故障,同时PC4是对该故障最敏感的主元,它的监测效果最好。
|
图 5 故障2在各主元方向上的监测散点图 Fig.5 Monitoring scatter plots of fault 2 in different principal directions |
TE过程主要有反应器、冷凝器、压缩机、分离器和汽提塔5个主要单元组成。该过程包含22个过程测量变量、19个成分测量变量以及12个操作变量[16-17]。本文选取22个过程测量变量以及除搅拌速度外的11个操作变量用于建模与监测,具体变量描述可见文献[16]。TE过程共包含21种故障,本文采集正常工况下的960个样本作为训练数据集,各种故障工况时的960个样本用作故障测试集,其中故障均从第161个样本点引入。
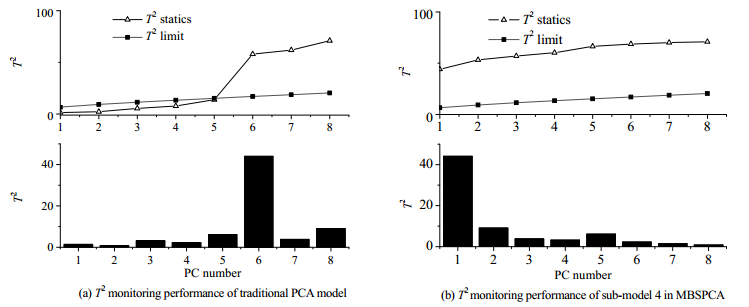
本文中PCA方法中主元个数采用CPV方法选取,累积方差贡献率取85%,MBSPCA方法中ω取0.2,即敏感主元阈值εlim为0.003 9,置信度α为0.99,β取0.99。图 6展示了故障16的监测结果,传统PCA方法没有很好地挖掘出数据中的故障信息,主元子空间中从第500个样本点开始持续报警,并在后续的监测中又下降到控制限以下,导致漏报率很高,同时残差子空间中也没有很好地挖掘出故障信息,而MBSPCA方法中将故障敏感主元放入到主元空间中进行监测,这样充分挖掘了图 6(c)是传统PCA方法中故障样本在选择不同主元个数时的T2统计量与故障控制限的比较以及各个主元上的T2统计量大小。点线图给出了T2统计量与T2控制限随着建模所用主元个数增加的变化曲线,柱状图表示每个主元方向的T2统计量贡献大小。在传统PCA方法中,只有选择主元个数大于25时,该模型才能有效地监测到故障10,这是由于前25个主元对该故障的监测不敏感,T2统计量的值均在一个很低的水平。由图 6(c)中可知对该故障最敏感的前4个主元分别是第27、31、28、26主元,但是通过CPV方法选择主元时,由于这些方差贡献度小的主元会排除,导致模型的监测性能很差。图 6(d)是MBSPCA方法中子块31每个主元方向上的T2统计量,变量31是故障16产生的主要原因,因此在子块31中以敏感系数ε排序的主元对故障的敏感程度是依次减少的,由此保证主元空间中总是包含了对故障最敏感的主元,进而提升了模型的监测性能。

|
图 6 TE过程故障16监测结果比较 Fig.6 Comparison of fault 16 monitoring results in TE processes |
表 2中给出了TE过程18种故障的监测结果。故障3、9、15在诸多方法均难以被监测到,所以在此不做比较。采用传统PCA方法、文献[13]中的SPCA方法、文献[16]中的FBPCA方法、文献[18]中的DPCA方法、文献[19]中的OP-PCA方法以及本文的MBSPCA方法做了对比,本文方法大多数故障下的漏报率最低,同时平均漏报率仅为6%均低于其他方法。除故障11、21之外,其余故障的漏报率均低于10%,且有7种故障的漏报率为0%。同时由于过程变量间具有一定的相关性,TE过程中故障发生时通常反应在多个变量上发生变化,针对这种类型故障,在监测时会有多个子块报警,最终反映到BIC统计量,因此本文方法也可以很好的监测多维变量上发生的故障。
|
|
表 2 TE过程18种故障监测结果比较(漏报率) Table 2 Comparison of 18 types of fault monitoring results in TE processes (missing alarm rates) |
表 3给出了MBSPCA、PCA对TE过程故障的误报率结果,在PCA方法中SPE的监测漏报率比T2统计量低,但同时其误报率却比T2高,因此在降低漏报率的同时也付出了一些代价。而MBSPCA方法中不仅漏报率大幅降低,同时误报率仅有0.314%,相比于PCA方法的0.696%有明显下降。该方法在降低漏报率的同时也降低了误报率,表现了良好的性能。
|
|
表 3 TE过程故障误报率比较(%) Table 3 Comparison of false alarm rates in TE processes (%) |
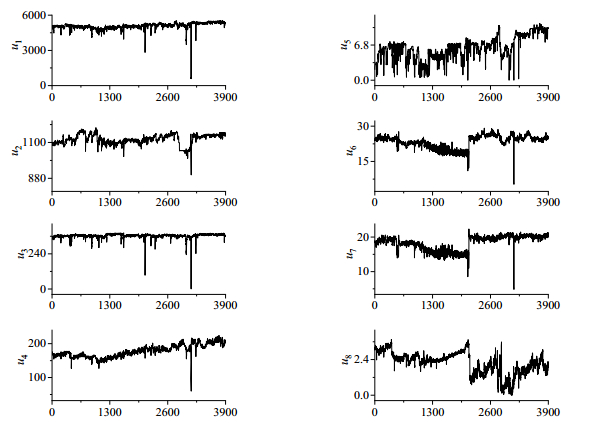
本文利用实际高炉炼铁过程数据验证本文方法的有效性。在高炉炼铁生产过程中,保持稳定的气流是保证铁水顺利生产的关键[20]。悬挂故障是由气体流动引起的一种典型故障,当上升的气流受到过量气体的限制或熔化的铁矿石导致炉腹架空时,通常会产生悬挂故障。如果悬挂故障未经修正,则炉顶压力和顶部热量会增加,最终,顶部结构可能会严重受损。本节考虑了一个真实高炉中发生悬挂故障的情况,高炉的内部容量为2 500 m3,采集了正常工况下的8个过程变量的2 000个样本。同时采集了1 900个悬挂故障条件下的测试样本,在悬挂故障条件下,炉顶压力上升,炉顶煤气的CO与CO2浓度增加,H2浓度下降。表 4给出了8个过程变量的描述, 同时图 7给出了各变量的变化曲线图,图中的后1 900个样本为故障样本。
|
|
表 4 悬挂故障监测中选择的变量 Table 4 Process variables selected for hanging fault monitoring |
|
图 7 高炉过程各变量曲线图 Fig.7 Profiles of variables in blast furnace process |
首先利用拉依达准则找出2 000个正常工况样本中的离群点,将这些点剔除后得到1 983个样本作为训练数据,然后对1 900个故障样本进行了测试。表 5给出了累积方差贡献率(CPV)取不同值时PCA方法的监测漏报率以及ω取不同值时MBSPCA方法的监测漏报率。结果显示PCA方法受主观参数CPV的影响,监测结果变化很大,结合图 8(b)可知,当CPV选取为0.9时,模型选择了前5个主元计算T2统计量的大小,由于第5主元的影响使得T2统计量漏报率下降至59.56%,当CPV为0.95时,由第6主元的影响使其漏报率降低至5.95%,但与此同时SPE的漏报率则上升至23.38%。而在MBSPCA方法中,第4子块中排序第一的主元的T2贡献度远大于其他主元,因此ω参数的变化对监测结果几乎没有影响。
|
|
表 5 不同参数下PCA与MBSPCA悬挂故障监测结果比较 Table 5 Comparison of hanging fault monitoring results under different parameters of PCA and MBSPCA |
|
图 8 高炉过程中两种方法的监测性能比较 Fig.8 Comparison of monitoring performance of the two methods in blast furnace processes |
本文提出了一种基于敏感主元选取的多块PCA化工过程故障监测方法。基于PCA故障监测模型中主元选择的重要性,通过分析T2统计量的构成定义了故障敏感系数ε,该系数反映了各主元对不同变量上发生的故障的敏感程度,并以此作为新的主元排序准则。考虑到实时监测过程中故障的未知性,针对过程的每一维变量建立一个子块模型,当故障发生在某一维或某几维变量上时,均会有相应的子块报警。最后利用贝叶斯信息构造BIC统计量,融合各个子块的监测结果。通过一个数值例子与TE过程和高炉炼铁过程的监测结果显示,该方法能够有效地提取过程中的故障敏感信息,克服了传统PCA算法的监测性能受主观参数累积方差贡献率的影响的缺点,同时有效地提升了监测精度。
| [1] |
郭金玉, 王鑫, 李元. 基于加权差分主元分析的化工过程故障检测[J]. 高校化学工程学报, 2018, 32(1): 183-192. GUO J Y, WANG X, LI Y. Fault detection in chemical processes using weighted differential principal component analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(1): 183-192. DOI:10.3969/j.issn.1003-9015.2018.01.025 |
| [2] |
QIN S J. Statistical process monitoring:Basics and beyond[J]. Journal of Chemometrics, 2003, 17(8/9): 480-502. |
| [3] |
GE Z Q, SONG Z H, GAO F R. Review of recent research on data-based process monitoring[J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562. |
| [4] |
Li W, YUE H H, Valle-Cervantes S, et al. Recursive PCA for adaptive process monitoring[J]. Journal of Process Control, 2000, 10(5): 471-486. DOI:10.1016/S0959-1524(00)00022-6 |
| [5] |
QIN S J, DUNIA R. Determining the number of principal components for best reconstruction[J]. Journal of Process Control, 2000, 10(2): 245-250. |
| [6] |
TAMURA M, TSUJITA S. A study on the number of principal components and sensitivity of fault detection using PCA[J]. Computers & Chemical Engineering, 2007, 31(9): 1035-1046. |
| [7] |
王海清, 余世明. 基于故障诊断性能优化的主元个数选取方法[J]. 化工学报, 2004, 55(2): 214-219. WANG H Q, YU S M. Selection of number of principal components based on fault diagnosing performance optimization[J]. Journal of Chemical Industry and Enginering (China), 2004, 55(2): 214-219. DOI:10.3321/j.issn:0438-1157.2004.02.015 |
| [8] |
XUAN J Y, XU Z, SUN Y. Selecting the number of principal components on the basis of performance optimization of fault detection and identification[J]. Industrial & Engineering Chemistry Research, 2015, 54(12): 3145-3153. |
| [9] |
PRIETO M A, LLANES S O, GARCIA M E. Principal components selection for dimensionality reduction using discriminant information applied to fault diagnosis[J]. Journal of Process Control, 2015, 33: 14-24. DOI:10.1016/j.jprocont.2015.06.003 |
| [10] |
陶阳, 王帆, 侍洪波. 基于Relief的主元挑选算法在过程监控中的应用[J]. 化工学报, 2017, 68(4): 1525-1532. TAO Y, WANG F, SHI H B, et al. Principal component selection algorithm based on relief and its application in process monitoring[J]. CIESC Journal, 2017, 68(4): 1525-1532. |
| [11] |
ZHAO C H, GAO F R. Fault-relevant principal component analysis (FPCA) method for multivariate statistical modeling and process monitoring[J]. Chemometrics & Intelligent Laboratory Systems, 2014, 133(1): 1-16. |
| [12] |
仓文涛, 杨慧中. 基于主元子空间富信息重构的过程监测方法[J]. 化工学报, 2018, 69(3): 1114-1120. CANG W T, YANG H Z. A process monitoring method based on informative principal component subspace reconstruction[J]. CIESC Journal, 2018, 69(3): 1114-1120. |
| [13] |
JIANG Q C, YAN X F, ZHAO W. Fault detection and diagnosis in chemical processes using sensitive principal component analysis[J]. Industrial & Engineering Chemistry Research, 2013, 52(4): 1635-1644. |
| [14] |
JOLLIFFE I T. A note on the use of principal components in regression[J]. Journal of the Royal Statistical Society, 1982, 31(3): 300-303. |
| [15] |
WANG Y, JIANG Q C, FU J. FRDPC subspace construction integrated with Bayesian inference for efficient monitoring of dynamic chemical processes[C]//Chinese Control Conference, Dalian: IEEE, 26-28 July, 2017: 7212-7217.
|
| [16] |
JIANG Q C, YAN X F, HUANG B. Performance-driven distributed PCA process monitoring based on fault-relevant variable selection and Bayesian inference[J]. IEEE Transactions on Industrial Electronics, 2015, 63(1): 377-386. |
| [17] |
ZHOU D H, LI G, QIN S J. Total projection to latent structures for process monitoring[J]. AIChE Journal, 2010, 56(1): 168-178. |
| [18] |
GE Z Q, SONG Z H. Distributed PCA model for plant-wide process monitoring[J]. Industrial & Engineering Chemistry Research, 2013, 52(5): 1947-1957. |
| [19] |
GHOSH K, RAMTEKE M, SRINIVASAN R. Optimal variable selection for effective statistical process monitoring[J]. Computers & Chemical Engineering, 2014, 60(60): 260-276. |
| [20] |
ZENG J, LUO S, CAI J, et al. Nonparametric density estimation of hierarchical probabilistic graph models for assumption-free monitoring[J]. Industrial & Engineering Chemistry Research, 2017, 56(5): 1278-1287. |




