气泡上浮运动过程广泛存在于船舶与海洋结构物以及能源与环境、化学工业以及军事技术等众多领域[1~3]。存在温差的气泡上浮过程中会与液体发生非等温传热传质过程,这直接决定了气体吸收、传播特性、气泡运动形态及结构等过程的效率。特别是其军事应用背景越来越强烈,作者率先提出的“舰船主机尾气抑制尾流技术”[4],因为能够有效降低舰船主机排放危害以及抑制尾流微气泡等作用,可有效提高舰船航行安全性并降低尾气排放危害性,已成为舰船尾流隐身技术研究的一个重要方向。而该技术的实现,正是将主机尾气在舰船底部通过装置进行排放。高温的尾气气体与低温海水液体迅速发生非等温传热、非平衡传质反应[5~7],直接影响气泡上浮速度、体积变化率等,从而影响尾流微气泡的消除抑制效果。
近些年来,国内外许多学者对气泡与液体间传热传质进行了研究,然而因气泡上浮过程往往较为复杂,多数研究未能对传热、传质、运动的影响因素综合考虑[8~9],且现有研究中,气泡传质模型的解算忽略了气泡密度、传热模型的解算近似处理为等温条件传热、气泡上浮过程忽略了附加质量力的脉动项等影响[10~12]。
为此,本文考虑气泡边界层的热传导微分方程和传质微分方程,对气泡绕流场速度进行一阶泰勒近似,并通过变量代换构建气泡非等温传热模型和瞬态非平衡传质模型;根据气泡受力情况,构建气泡瞬态加速度表达式;并结合气泡半径微分方程,构建高温气泡上浮与传热传质过程的完整耦合模型。
2 气泡上浮基本模型为综合研究传热、传质与速度、半径等不同因素对气泡上浮运动特性的影响规律,需要分别建立静水条件下气泡的非等温传热微分方程、瞬态非平衡传质微分方程、速度微分方程以及半径微分方程。
2.1 气泡传热微分方程气泡热边界层的热传导微分方程为[13]:
| $ {u_\text{r}}\frac{{\partial t}}{{\partial r}} + \frac{{{u_\rm{\theta} }}}{R}\frac{{\partial t}}{{\partial \theta }} = \alpha \frac{{{\partial ^2}t}}{{\partial {r^2}}} $ | (1) |
r和θ是以气泡中心为原点的球坐标系坐标。由于气泡上浮速度小,绕流雷诺数低,其速度场ur和uθ可表示如下式[13],并进行泰勒近似:
| $ {{u}_\text{r}}=-{{v}_\text{b}}(1-\frac{3R}{2r}+\frac{{{R}^{3}}}{2{{r}^{3}}})\cos \theta \approx -\frac{3}{2}{{v}_\text{b}}{{(\frac{r-R}{R})}^{2}}\cos \theta $ | (2) |
| $ {u_\rm{\theta} } = \frac{1}{2}{v_\text{b}}(2 - \frac{{3R}}{{2r}} - \frac{{{R^3}}}{{2{r^3}}})\sin \theta \approx \frac{3}{2}{v_\text{b}}\frac{{r - R}}{R}\sin \theta $ | (3) |
构造函数
| $ - {M^2}\frac{{\partial t}}{{\partial M}} = \frac{{{\partial ^2}t}}{{\partial {M^2}}} $ | (4) |
解式(4)得:
| $ t = {A_1}\int_0^M {\text{exp}( - {x^3}/3)\text{d}x} + {A_2} $ | (5) |
其中A1和A2为待定常数。
由于高温气泡体积小,内部分子运动剧烈,热传递充分,可以认为tg处处相同,且tl恒定。根据边界条件有:当r = R时,t = tg,M|r=R = 0,得A2 = tg;当r = +∞时,t = tl,M|r=+∞
= +∞,
由此可得到气泡传热边界层的温度分布,进而计算得气泡表面的热流密度为:
| $ q=\lambda \cdot \frac{\partial t}{\partial r}{{|}_{r=R}}=\frac{\lambda }{\Gamma (1/3)}\cdot {{(\frac{18{{v}_\text{b}}}{\alpha {{R}^{2}}})}^{{1}/{3}\;}}\cdot ({{t}_\text{l}}-{{t}_\text{g}})\cdot \frac{\sin \theta }{{{(2\theta -\sin 2\theta )}^{{1}/{3}\;}}} $ | (6) |
由上式可得平均热流密度:
| $ \overline{q}=\frac{1}{4\pi {{R}^{2}}}\int\limits_{0}^{\pi }{2\pi {{R}^{2}}q\sin \theta \text{d}\theta }={{(\frac{243{{\pi }^{2}}}{8\alpha })}^{{1}/{3}\;}}\frac{\lambda }{4\Gamma (1/3)}\cdot ({{t}_\text{l}}-{{t}_\text{g}})\cdot {{R}^{-{2}/{3}\;}}\cdot v_\text{b}^{{1}/{3}\;} $ | (7) |
由式(7)解得气泡内部的温度tg为:
| $ {{t}_\text{g}}={{t}_\text{l}}-\overline{q}\cdot {{(\frac{243{{\pi }^{2}}}{8\alpha })}^{{-1}/{3}\;}}\frac{4\Gamma (1/3)}{\lambda }\cdot {{R}^{{2}/{3}\;}}\cdot v_\text{b}^{-{1}/{3}\;} $ | (8) |
所以tg对时间的微分:
| $ \frac{1}{{{t_\text{g}} - {t_\text{l}}}}\frac{{\text{d}{t_\text{g}}}}{{\text{d}\tau }} = \frac{1}{q}\frac{{\text{d}q}}{{\text{d}\tau }} + \frac{2}{{3R}}\frac{{\text{d}R}}{{\text{d}\tau }} - \frac{1}{{3{v_\text{b}}}}\frac{{\text{d}{v_\text{b}}}}{{\text{d}\tau }} $ | (9) |
又因为有能量关系:
| $ {{\text{c}}_{\text{g}}}(m-\text{ }\!\!\delta\!\!\text{ }m)\text{ }\!\!\delta\!\!\text{ }{{t}_{\text{g}}}\text{+}{{\text{c}}_{\text{g}}}\text{ }\!\!\delta\!\!\text{ }m({{t}_{\text{g}}}\text{-}{{t}_{\text{l}}})\text{=}Sq\text{ }\!\!\delta\!\!\text{ }\tau $ | (10) |
忽略二阶小量δmδtg,取微分整理得到:
| $ \frac{\text{d}{{t}_{\text{g}}}}{\text{d}\tau }=\frac{Sq}{{{c}_{\text{g}}}m}-\frac{{{t}_{\text{g}}}-{{t}_{\text{l}}}}{m}\frac{\text{d}m}{\text{d}\tau } $ | (11) |
联立式(9)和(11)得:
| $ \frac{\text{d}q}{\text{d}\tau }=q[\frac{Sq}{{{c}_{\text{g}}}m({{t}_{\text{g}}}-{{t}_{\text{l}}})}-\frac{2}{3R}\frac{\text{d}R}{\text{d}\tau }+\frac{1}{3{{v}_{\text{b}}}}\frac{\text{d}{{v}_{\text{b}}}}{\text{d}\tau }-\frac{1}{m}\frac{\text{d}m}{\text{d}\tau }] $ | (12) |
式(11)和(12)即为高温气泡的传热微分方程。
2.2 气泡传质微分方程气泡传质边界层中浓度c的微分方程为[13]:
| $ {u_{\rm{r}}}\frac{{\partial c}}{{\partial r}} + \frac{{{u_{{\rm{\theta }}}}}}{R}\frac{{\partial c}}{{\partial \theta }} = D\frac{{{\partial ^2}c}}{{\partial {r^2}}} $ | (13) |
同1.1节中的方法,解得气泡传质边界层的浓度分布为:
| $ \begin{align} &\ \ \ \ c=\frac{{{3}^{{2}/{3}\;}}}{\Gamma (1/3)}\cdot ({{c}_{\text{a}}}-{{c}_\text{i}})\cdot \int\limits_{0}^{M}{{\text{e}^{-{{{x}^{3}}}/{3}\;}}}\text{d}x+{{c}_\text{i}} \\ &M={{(\frac{2{{v}_\text{b}}}{D{{R}^{2}}})}^{{1}/{3}\;}}\cdot (r-R)\cdot \frac{\sin \theta }{{{(2\theta -\sin 2\theta )}^{{1}/{3}\;}}} \\ \end{align} $ | (14) |
所以气泡界面上的质量流量为:
| $ J=D\cdot \frac{\partial C}{\partial r}{{|}_{r=R}}=\frac{1}{\Gamma (1/3)}\cdot {{(\frac{18{{v}_\text{b}}{{D}^{2}}}{{{R}^{2}}})}^{{1}/{3}\;}}\cdot ({{c}_{\text{a}}}-{{c}_\text{i}})\cdot \frac{\sin \theta }{{{(2\theta -\sin 2\theta )}^{{1}/{3}\;}}} $ | (15) |
由气泡瞬态传质表达式,得气泡传质微分方程:
| $ \begin{align} &\frac{\text{d}m}{\text{d}\tau }={{(\frac{243}{8})}^{{1}/{3}\;}}\cdot \frac{({{c}_{\text{a}}}-{{c}_\text{i}})}{\Gamma (1/3)}\cdot {{\pi }^{{5}/{3}\;}}{{D}^{{2}/{3}\;}}{{R}^{{4}/{3}\;}}v_\text{b}^{{1}/{3}\;} \\ &\text{ }H{{P}_{\text{g}}}{{c}_{\text{i}}}=\text{exp }\!\![\!\!\text{ 2}({{c}_{\text{a}}}-{{c}_{\text{i}}})/\left( {{c}_{\text{a}}}+{{c}_{\text{i}}} \right)\text{ }\!\!]\!\!\text{ } \\ &\begin{matrix} {}&{} \\ \end{matrix}{{P}_\text{g}}={{P}_\text{atm}}+{{\rho }_\text{l}}g(h-z)+2\sigma /R \\ \end{align} $ | (16) |
假设气泡运动过程中保持稳定的球状外形,且水平方向受力平衡,忽略卡门涡街效应及气泡间相互作用。气泡在静水中的牛顿第二定律方程为:
| $ \frac{4}{3}\pi {R^{\rm{3}}}{\rho _{\rm{g}}}\frac{{\text{d}{v_\text{b}}}}{{\text{d}\tau }} = {F_V} - {F_\text{G}} - {F_\text{B}} - {F_\text{m}} - {F_\text{D}} $ | (17) |
式中,浮力FV = 4πgR3ρl/3,重力FG = 4πgR3ρg/3,Basset力
| $ \frac{{{\rm{d}}{v_{\rm{b}}}}}{{{\rm{d}}\tau }} = \frac{{2{\rho _\rm{l}}}}{{{\rho _\rm{l}} + 2{\rho _{\rm{g}}}}}(\frac{{{\rho _{\rm{l}}} - {\rho _{\rm{g}}}}}{{{\rho _{\rm{l}}}}}{\rm{g}} - \frac{3}{8}{C_{\rm{d}}}\frac{{v_{\rm{b}}^{\rm{2}}}}{R} - \frac{{3{v_{\rm{b}}}}}{{2R}}\frac{{{\rm{d}}R}}{{{\rm{d}}\tau }} - \frac{9}{{2R}}\sqrt {\frac{{\rm{\mu }}}{{{\rm{\pi }}{\rho _{\rm{l}}}}}} \int_0^\tau {\frac{{{\rm{d}}{v_{\rm{b}}}/{\rm{d}}t}}{{\sqrt {\tau - t} }}} {\rm{d}}t) $ | (18) |
气泡内部的气体可看作理想气体,满足克拉伯龙方程:
| $ {P_{\rm{g}}} = N{\rho _{\rm{g}}}{t_{\rm{g}}} $ | (19) |
又对气泡有[18]:
| $ \frac{{{\rm{d}}m}}{{{\rm{d}}\tau }} = \frac{4}{3}{\rm{\pi }}{R^2}(R\frac{{{\rm{d}}{\rho _{\rm{g}}}}}{{{\rm{d}}\tau }} + 3{\rho _{\rm{g}}}\frac{{{\rm{d}}R}}{{{\rm{d}}\tau }}) $ | (20) |
对式(19)中的ρg求时间的微分,并联立式(20)得到气泡半径微分方程:
| $ (\frac{{3{\rho _{\rm{g}}}{t_{\rm{g}}}}}{{NR}} - \frac{{2{\rm{\sigma }}}}{{{R^2}}})\frac{{{\rm{d}}R}}{{{\rm{d}}\tau }} = (\frac{{{\rho _{\rm{g}}}{t_{\rm{g}}}}}{{Nm}}\frac{{{\rm{d}}m}}{{{\rm{d}}\tau }} + \frac{{{P_{\rm{g}}}}}{{{t_{\rm{g}}}}}\frac{{{\rm{d}}{t_{\rm{g}}}}}{{{\rm{d}}\tau }} + {\rho _{\rm{l}}}{\rm{g}}{v_{\rm{b}}}) $ | (21) |
为了更精确地表征高温气泡上浮运动中各影响因素的相互作用规律,需要综合上述各特征微分方程,构建气泡运动耦合模型,并根据初始条件进行数值解算,将所建立的耦合模型与当前仿真及实验数据进行对比,以验证模型的正确性。
3.1 模型的构建以气泡初始位置为坐标原点建立直角坐标系,运动取垂直向上为正,上浮距离z为该方向上的位移。联立气泡传热微分方程式(11)和(12),传质微分方程式(16),速度微分方程式(18)以及半径微分方程式(21),得到液体中高温气泡上浮运动的耦合模型。值得提出的是,若将传热微分方程均取零,则得到水中气泡的等温上浮运动模型。
模型中的初始条件为:海水温度t1,气泡初始温度tg0,释放深度h,初始上浮距离z0 = 0,初始半径R0,初始密度ρg0 = (Patm+ρlgh+2σ/R0)/(Ntg0),初始质量m0 = 4πρg0R03/3,初始速度vb0 = 0,初始热流密度
利用四阶龙格库塔法对模型进行数值模拟。由于Basset力的积分式中包含奇异端点,因此解算速度微分方程时,需先处理其中的广义积分项。将气泡运动时间τ分割为离散的时间点{τ0, τ1, …, τn},其中τ0 = 0,τn = τ,Δτn = τn-τn-1,并记加速度a(τ) = dvb/dτ,由复化梯形公式和微分中值定理可得到积分项的离散表达式:
| $ B = \int_0^\tau {\frac{{{\rm{d}}{v_{\rm{b}}}/{\rm{d}}t}}{{\sqrt {\tau - t} }}} {\rm{d}}t = \frac{{\Delta {\tau _1}}}{2}\frac{{a(0)}}{{\sqrt {{\tau _n}} }} + \sum\limits_{i = 1}^{n - 2} {\frac{{\Delta {\tau _i}a({\tau _i})}}{{\sqrt {{\tau _n} - {\tau _i}} }}} + (\frac{{\Delta {\tau _{n - 1}}}}{{2\sqrt {{\tau _n} - {\tau _{n - 1}}} }} + \frac{{\Delta {\tau _n}}}{{2\sqrt {\Delta {\tau _{n - 1}}} }})a({\tau _{n - 1}}) + \frac{{\sqrt {\Delta {\tau _n}} }}{2}a({\tau _n}) $ | (22) |
注意上式中a(τn) = a(τ),所以代入速度微分方程时,需要对方程重新整理:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}{v_{\rm{b}}}}}{{{\rm{d}}\tau }} = \frac{{2({k_2} - {k_1}B)}}{{2 + {k_1}\sqrt {\Delta {\tau _n}} }}}\\ {{k_1} = \frac{9}{{R({\rho _{\rm{l}}} + 2{\rho _{\rm{g}}})}}\sqrt {\frac{{{\rm{\mu }}{\rho _\text{l}}}}{{\rm{\pi }}}} }\\ {{k_2} = \frac{{2{\rho _{\rm{l}}}}}{{{\rho _{\rm{l}}} + 2{\rho _{\rm{g}}}}}(\frac{{{\rho _{\rm{l}}} - {\rho _{\rm{g}}}}}{{{\rho _{\rm{l}}}}}{\rm{g}} - \frac{3}{8}{C_{\rm{d}}}\frac{{v_{\rm{b}}^{\rm{2}}}}{R} - \frac{{3{v_{\rm{b}}}}}{{2R}}\frac{{{\rm{d}}R}}{{{\rm{d}}\tau }})} \end{array}} \right. $ | (23) |
为验证耦合模型的准确性,通过实验测定气泡上浮速度及半径,并将数值模拟结果及实验测定的研究结果进行对比。
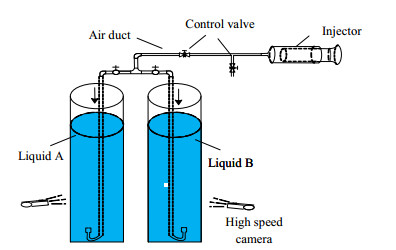
4.1 实验设计实验研究目的是得出气泡在液体中上升过程的半径及瞬时稳态上升速度。为此,专门研制了相应的实验装置,如图 1所示。实验时利用室温20℃、常压下的空气生成气泡。冰水混合调整液体温度(0,15,45和75℃),利用圆柱桶依次、反复进行盛装并进行实验。在实验室条件下,气泡上浮测定实验装置使用自然光光源、高速摄影技术、图像处理技术等方法对气泡运动实验数据进行获取。利用短曝光时间高速相机对不同气泡源进行了测量分析。
|
图 1 气泡上浮测定实验装置图 Fig.1 Experimental facility of bubble flotation measurement |
实验步骤如下:
第一步:数据采集。将室温、常压下的空气从注射器经进气管缓慢注入不同温度液体中,形成单气泡上浮运动,高速摄像机对气泡运动进行记录。
第二步:数据存储及图像筛选。所获取气泡运动影像通过电脑屏幕展现,逐帧播放并筛选气泡上浮半径及瞬时稳态速度图像。在图像的相邻两帧间隔时间,根据气泡质心上浮高程计算气泡瞬时稳态上浮速度[19]。
第三步:数据处理。将筛选的气泡运动图像保存为BMP格式,使用Matlab程序对其进行灰度及二进制转化处理。
选取初始半径为800 μm的气泡,释放深度H = 1 m,气泡从孔口上升一段距离后,受力达到平衡,速度将稳定不变。距离孔口75 mm处,气泡即可达到稳定上升状态。本实验为确保气泡有足够上升高度,在300~400 mm进行速度测量。
4.2 数据分析对4种温度液体分别进行15组重复实验,测定气泡上浮半径及瞬时稳态上浮速度,淘汰实验结果中起伏较大的数据,获得每组实验中相近的10组数据,并求取平均值以减小随机误差。需要强调的是,气泡运动模型主要针对气泡竖直方向,因此气泡速度的测定计算也仅考虑竖直方向。
每组实验中所采集的图像,通过编程,转换成灰度归一化图,气泡生长及上浮过程典型运动状态的照片经处理后,如图 2所示,其中(a)为气泡生长过程典型状态,(b)为气泡上浮过程典型状态。图像经处理过程中,未对气泡质心位置造成影响,可有效降低误差。

|
图 2 经处理后的气泡运动状态照片 Fig.2 Images of bubble movement after processing |
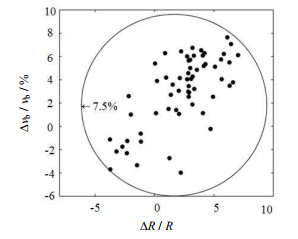
利用耦合模型对不同上浮距离处的气泡半径及运动速度进行数值模拟,常量参数设置依照普通空气及室温水,气泡变量参数设置:半径800 μm,释放深度1 m,密度1.344 kg·m-3 (式(19)计算),由静止状态下上浮。将数值计算结果与实验数据对比,为便于研究气泡半径的变化规律,对其进行了归一化处理。所得相对误差分布如图 3所示,最大偏差为7.64%,具有较高的吻合度。误差精度为7.8%,精确度高。验证表明,该耦合模型能够一定程度模拟高温气泡上浮过程的运动规律,较好地验证了模型和数值计算方法的正确性。
|
图 3 气泡半径、速度相对误差分布 Fig.3 Relative error distribution of bubble radius and velocity |
由散点图还可知,速度误差值普遍大于半径误差,主要因为在测量过程中,在特点高度中,通过高速摄像机可以较为准确的测定气泡上浮半径,而上浮速度的测定基础是短暂上升时间内的高度值,而且气泡上浮半径误差的增大将引起气泡加速度及速度误差的增大,因此在实验测量中出现如图误差分布情况。验证表明,该耦合模型能够准确模拟气泡在整个上浮过程的运动规律,有效验证了模型和数值计算方法的正确性。
4.3 对比验证气泡在液体中的上浮运动,可分为运动初期的非等温传热传质过程及其后的等温传质过程。因为初期的非等温传热过程极短,难以通过有限的实验条件进行测定验证,所以本文将该短暂的过程与文献[8]的研究结果进行对比。文献中对初始温度为900 K的气泡在323 K的液体中的传热传质过程进行仿真,研究气泡收缩过程中半径减小幅度R/R0的变化规律,结论可有效预测气体蒸发速率和持气率实验的相关结果。
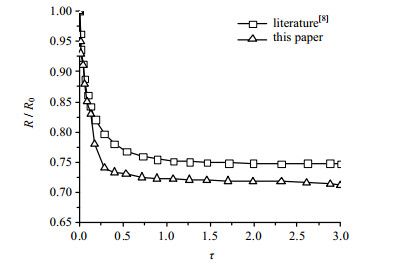
气泡运动的非等温传热传质过程,将根据上述耦合模型解算出的半径变化曲线与文献[8]的结论比较,如图 4所示,最大偏差为5%,具有较高的吻合度。验证表明,该耦合模型能够准确模拟气泡上升初期的非等温传热过程规律,能够有效验证了该模型和数值计算方法的正确性。
|
图 4 无量纲气泡半径R/R0的变化曲线 Fig.4 Profiles of dimensionless bubble radius R/R0 |
为探讨传热、传质、外界压强对液体中气泡上浮运动的影响,对三者与气泡上浮半径关系进行仿真计算。设定气泡释放深度为10 m,液体温度为290 K,气体温度为690 K。
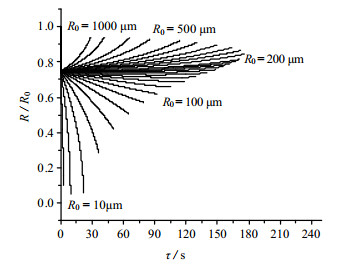
5.1 气泡半径界定标准对初始半径为5~1000 μm的气泡半径变化趋势进行仿真,如图 5所示。由图可见,随气泡初始半径的不同,气泡半径变化规律有所差异。将图 5中半径密集部分放大如图 6所示。
|
图 5 气泡半径变化曲线(整体) Fig.5 Profiles of bubble radius variation (global) |
|
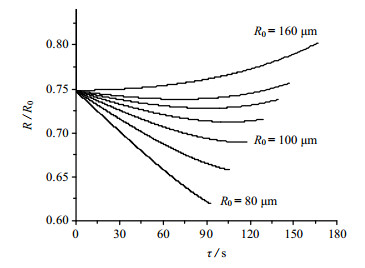
图 6 气泡半径变化曲线(局部) Fig.6 Profiles of bubble radius variation (local) |
由气体状态方程知R3~T,并根据图 5、6得,相同温度下,气泡半径比R/R0均先迅速减小至约0.745,随后气泡半径规律出现差异。当为大半径气泡(R0 > 160 μm)时,气泡在上升过程中,半径呈逐渐增大趋势,且气泡初始半径越大,其增大幅度越明显。而当为小半径气泡(R0 < 80 μm)时,规律相反,即气泡在上升过程中,半径呈逐渐减小趋势,且气泡初始半径越小,其减少幅度越明显。当为中等半径气泡(80 μm ≤ R0 ≤ 160 μm)时,气泡在上浮过程中,半径呈先减小后增大的趋势。因此分别对三种类型气泡运动影响规律进行探讨。
5.2 气泡运动影响规律 5.2.1 大半径气泡对初始半径为500 μm的大气泡上浮运动进行仿真。大气泡运动影响因素初期及整体如图 7、8所示。
|
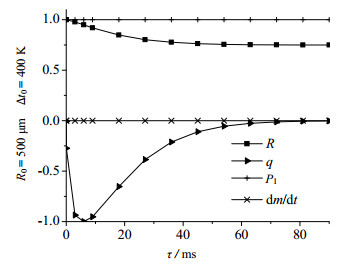
图 7 大气泡半径影响因素(初期) Fig.7 Effects of different factors on big bubble radius (initial) |
|
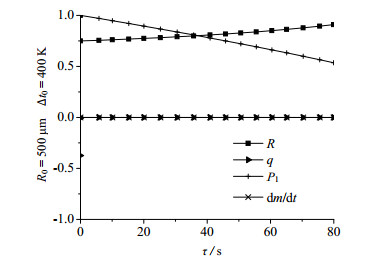
图 8 大气泡半径影响因素(全过程) Fig.8 Effects of different factors on big bubble radius (whole process) |
在大气泡上浮初期,气泡热流密度大,传递的热量多,温度变化加快,大气泡半径急剧变小。而此时气泡质量变化缓慢,质量传递不是主导因素,迅速传热起到重要作用,气泡半径主要随温度的降低而迅速减小。当气泡温度降至液体温度时,气泡上升运动主要受压强作用,此时气泡半径呈稳定缓慢的增大趋势。由图可知,在整个过程中,传质相较传热及压强的影响,均稳定在一个相对低的水平。
5.2.2 中等半径气泡定义中等气泡半径为80 μm ≤ R0 ≤ 160 μm,本文对初始半径为150 μm的中等气泡上浮运动进行仿真。中等气泡运动影响因素初期及整体如图 9、10所示。
|
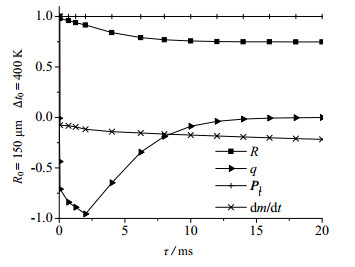
图 9 中等气泡半径影响因素(初期) Fig.9 Effects of different factors on medium bubble (initial) |
|
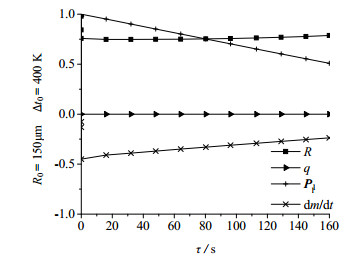
图 10 中等气泡半径影响因素(全过程) Fig.10 Effects of different factors on big bubble radius (whole process) |
中等气泡半径在上浮过程中,气泡在传热、传质及压强的共同作用下,呈先减小后缓慢增大的趋势。在气泡上浮初始阶段,压强没有较明显变化,而气液快速传热过程及传质作用使气泡半径快速减小。随着中等气泡上浮进行,气泡降至液温后,质量流失使气泡缩小,压强降低使气泡膨胀,两者共同影响气泡半径变化。但总体而言,气泡所受液压随临近液面而减小明显,使压强起主导作用,气泡半径缓慢增加。
5.2.3 小半径气泡对初始半径为20 μm的小气泡上浮运动仿真。小气泡运动影响因素初期及整体如图 11、12所示。
|
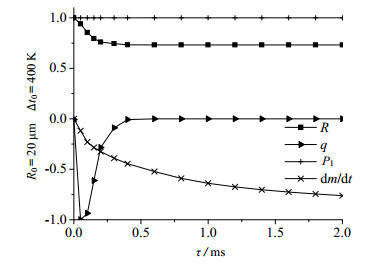
图 11 小气泡半径影响因素(初期) Fig.11 Effects of different factors on small bubble radius (initial) |
|
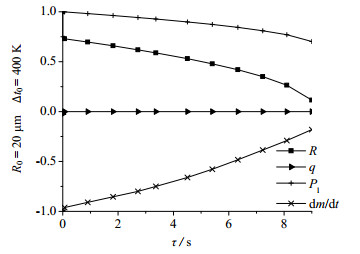
图 12 小气泡半径影响因素(整体) Fig.12 Effects of different factors on small bubble radius (whole process) |
由图可知,压强对小气泡运动的影响变化微弱。在小气泡上浮初期,气泡热量的迅速降低、质量的加速减少使气泡体积急剧收缩,半径随之减小。因气泡携带热量更低,小气泡的非等温传热时间仅约为0.5 ms远小于大气泡的65 ms。随气泡热量散失,小气泡半径则主要受传质及压强影响,半径缓慢减小直至气泡消失。
由以上分析可知,气泡在上浮过程中,运动特性受传热、传质、压强的共同影响。
① 传质:传质对不同尺度气泡影响不同,小气泡在传质主导作用下加速消失;传质影响中等气泡半径降低,但不起决定作用;对大气泡的影响微弱可忽略。因为根据传质微分方程式(16),可得到传质效率dm/(mdτ)正比于R-5/3,随着气泡半径的增大,气泡传质效率降低,对大于160 μm的气泡而言,传热、压强的变化是影响气泡半径的主导因素。
② 传热:气泡在液体中上浮运动的初期为非等温传热传质过程,热量会迅速散失。但因气泡携带热量有限,其在水中的非等温传热过程极短。气泡的主要降温过程是在与水接触的初始阶段内迅速完成,随着接触时间的延长,气泡的温度也将急剧下降至接近液温。根据平均热流密度方程式(7),可得到∂q/∂R和∂q/∂vb分别与R-5/3和vb-2/3呈正比。因此大气泡因初始半径大,携带能量多,冷却收缩过程相对更慢,所以热流密度的变化幅度也相对更加缓慢,热传导效率更低,非等温传热过程时间有所延长。
③ 压强:在气泡上升过程中,压强对气泡运动特性影响基本保持不变。但因液体中气泡压强公式为P = ρlgh,大气泡上浮速度快,一定时间内上浮距离大,所以相较于小气泡,大气泡压强下降大。
6 结论本文根据高温气泡上浮运动特点,分别建立气泡传热、传质、运动及半径微分方程,根据各过程的关联因素,建立气泡上浮与传热传质过程的完整耦合模型。利用四阶龙格库塔法对模型进行解算仿真。为对模型进行更全面的验证,将气泡非等温传热过程与当前研究进行对比;并设计实验测定不同温度液体中气泡上浮半径及瞬时稳态上浮速度,将不同上浮距离处的数值计算结果与实验数据对比。验证液体中气泡上浮与传热传质的耦合模型的准确性。
利用该耦合模型对不同半径气泡的运动影响规律进行研究,可知:气泡在上浮过程中,运动特性受传热、传质、压强的共同影响。并获得如下主要结论:
1) 传质对不同尺度气泡的影响不同,小气泡在传质作用下加速消失,并使中等气泡半径持续降低,但对大气泡的影响微弱可忽略。
2) 气泡在液体中上浮运动的初期为非等温传热过程,热量会迅速散失,半径快速下降。气泡尺度越小,热流密度的变化幅度更加明显,热传导效率更高,非等温传热过程加速结束。
3) 在气泡上升过程中,压强对气泡运动影响基本保持不变。但从整体而言,随气泡半径增大,压强下降速率略微增快。
4) 随非等温传热影响消失,大气泡半径呈稳定、缓慢的增大;中等气泡半径呈缓慢的先减小再增大趋势;而小气泡逐渐溶解在液体中。
本文是在静水条件下,利用数值模拟获得考虑传热传质耦合气泡的上浮特性变化规律,可以为“基于主机尾气的舰船尾流消除技术”的实现提供有效的参考依据,并且模型及结论对众多领域中气泡上浮运动过程具有普适性,可作为深入研究的理论基础。
符号说明:
|
|
| [1] | QIU C, ZHANG H C. Effects of system pressure and heat flux on bubble nucleation and growth[J]. Chinese Journal of Mechanical Engineering , 2015, 28(5): 964-970. DOI:10.3901/CJME.2015.0703.086. |
| [2] | Giorgio Besagni, Pietro Brazzale, Alberto Fiocca. Estimation of bubble size distributions and shapes in two-phase bubble column using image analysis and optical probes[J]. Flow Measurement and Instrumentation , 2016, 52(1): 77-85. |
| [3] | OUYANG Di-hua(欧阳的华). Dynamic model of bubble induced by the interaction between pyrotechnic composition combustion particles and water(烟火药水下燃烧高温粒子与水作用的气泡动力学模型)[J]. Chinese Journal of Energetic Materials(含能材料) , 2013, 21(4): 460-463. |
| [4] | JIN Liang-an(金良安), ZHANG Zhi-you(张志友), YUAN Zhi-jiang(苑志江), et al. Problems in ship wake stealth technology and countermeasures(舰船尾流隐身技术的问题与对策思考)[J]. Shipbuilding of China(中国造船) , 2017, 58(1): 177-185. |
| [5] | ZHANG Bin(张斌), LI Jian-bo(李见波), WU Shu-mei(吴淑梅). Investigation on diesel engine modeling based on Matlab and EU Ⅵ calibration method(基于Matlab的柴油机建模及欧-Ⅵ标定方法研究)[J]. Chinese Internal Combustion Engine Engineering(内燃机工程) , 2016, 37(2): 101-104+110. |
| [6] | Naval Command (海军司令部). Naval High-tech knowledge textbook(海军高技术知识教材)[M].Beijing(北京): Naval Command(海军司令部), 1997: 121-123. |
| [7] | HUA J S, LOU J. Numerical simulation of bubble rising in viscous liquid[J]. Journal of Computational Physics , 2007, 222(2): 769-795. DOI:10.1016/j.jcp.2006.08.008. |
| [8] | Campos F B, Lage P L C. Simultaneous heat and mass transfer during the ascension of superheated bubbles[J]. International Journal of Heat and Mass Transfer , 2000, 43(2): 179-189. DOI:10.1016/S0017-9310(99)00143-X. |
| [9] | TAO Ye-sheng(陶烨晟), WANG Li-feng(王立锋), YE Wen-hua(叶文华), et al. The bubble velocity research of Rayleigh-Taylor and Richtmyer-Meshkov instabilities at arbitrary Atwood numbers(任意Atwood数Rayleigh-Taylor和Richtmyer-Meshkov不稳定性气泡速度研究)[J]. Acta Physica Sinica(物理学报) , 2012, 61(7): 314-320. |
| [10] | WU Fang(吴芳), WU Hua-jie(吴华杰), CUI Guo-qi(崔国起). Visualization experiment for bubble generation of subcooled flow boiling(过冷流动沸腾气泡生成状态的可视化实验研究)[J]. Journal of Engineering Thermophysics(工程热物理学报) , 2016, 37(11): 2417-2423. |
| [11] | CHEN Ying-yu(陈莹玉), YAO Xiong-liang(姚熊亮). Dynamics of underwater explosion bubble near free surface(近水面水下爆炸气泡强耦合运动特性研究)[J]. Shipbuilding of China(中国造船) , 2016, 57(3): 65-71. |
| [12] | Giorgio Besagni, Pietro Brazzale, Alberto Fiocca. Estimation of bubble size distributions and shapes in two-phase bubble column using image analysis and optical probes[J]. Flow Measurement and Instrumentation , 2016, 52: 190-207. DOI:10.1016/j.flowmeasinst.2016.10.008. |
| [13] | DAI Gan-ce(戴干策), CHEN Min-heng(陈敏恒). Chemical Engineering Fluid Mechanics(化工流体力学)[M].Beijing(北京): Chemical Industry Press(化学工业出版社), 1988: 256, 276, 374. |
| [14] | TIAN Heng-dou(田恒斗), JIN Liang-an(金良安), CHI Wei(迟卫), et al. Impact of Basset force on the movement of soluble bubble in fluid(Basset力对液体中易溶性气泡运动的影响)[J]. Chinese Journal of Theoretical and Applied Mechanics(力学学报) , 2011, 43(4): 680-687. DOI:10.6052/0459-1879-2011-4-lxxb2010-069. |
| [15] | Yoshida K, Fujikawa T, Watanabe Y. Experimental investigation on reversal of secondary Bjerknes force between two bubbles in ultrasonic standing wave[J]. The Journal of the Acoustical Society of America , 2011, 130(1): 135-144. DOI:10.1121/1.3592205. |
| [16] | ZHANG A M, NI B Y. Influences of different forces on the bubble entrainment into a stationary Gaussian vortex[J]. Science China Physics, Mechanics and Astronomy , 2013, 56(11): 2162-2169. DOI:10.1007/s11433-013-5267-2. |
| [17] | Carrica P M, Bonetto F J, Drew D A, et al. The interaction of background ocean air bubbles with a surface ship[J]. International Journal for Numerical Methods in Fluids , 1998, 28(4): 571-600. DOI:10.1002/(ISSN)1097-0363. |
| [18] | TIAN Heng-dou(田恒斗), JIN Lian-an(金良安), DING Zhao-hong(丁兆红), et al. Coupling model for bubble rise and mass transfer process in liquid(液体中气泡上浮与传质过程的耦合模型)[J]. Journal of the Chemical Industry and Engineering Society of China(化工学报) , 2010, 61(1): 15-21. |
| [19] | DAI Xiao-wei(代晓巍), JIN Liang-an(金良安), CHI Wei(迟卫). Analysis technique to dissolution rate of rising bubble in water based on two-direction images(基于双向图像的水中上升气泡溶解速率分析技术)[J]. Journal of the Chemical Industry and Engineering Society of China(化工学报) , 2011, 62(2): 315-320. |




