近年来,两相流凭借其良好的传热性能广泛应用于化工、石油及核反应堆等领域[1]。与此同时,船舶及漂浮式核能海水淡化等行业也处于飞速发展阶段[2-4],受海洋等自然条件的影响,设备元件会发生倾斜、摇摆及振动等情况[5-6],进而影响气液两相流动情况及设备的安全运行[7]。
目前,国内外学者对摇摆状态下通道内两相流动规律进行大量研究[8-12]。张金红等[13]通过研究摇摆状态下的圆管内流型,发现流型随摇摆周期发生周期性变化。曹夏昕等[14]通过对单相水阻力特性的研究发现摇摆明显改变管内摩擦阻力系数。与之相比,对非线性振动工况下流体流动的研究则鲜有报道。事实上,两相流是一个复杂的非线性动力学系统,由于气液相界面存在复杂的界面效应,其内部流动结构变化与压力波动信号有着紧密的联系[15-17]。PENDYALA等[18-19]通过研究振动工况下垂直管内两相流动及压降,得出低频振动可以加大流体流速及压降波动。JING等[20]实验研究波动条件下狭长窄矩形通道内空隙率的分散情况。BARNEA等[21]通过改变倾斜通道角度实验研究流型转变规律。由此可见,国内外学者对非线性振动下倾斜通道内气液两相流型及流型转换界限等尚未得出统一的结论。
鉴此,为进一步揭示非线性振动对倾斜通道内流体流动的影响,避免振动工况下不利于设备安全运行的流型出现,本文通过实验对比不同振动参数及倾角对流型转换界限及空隙率的影响,并探讨适用于非线性振动工况下倾斜通道内空隙率的计算方法,以期为工程实际应用提供一定的安全保障。
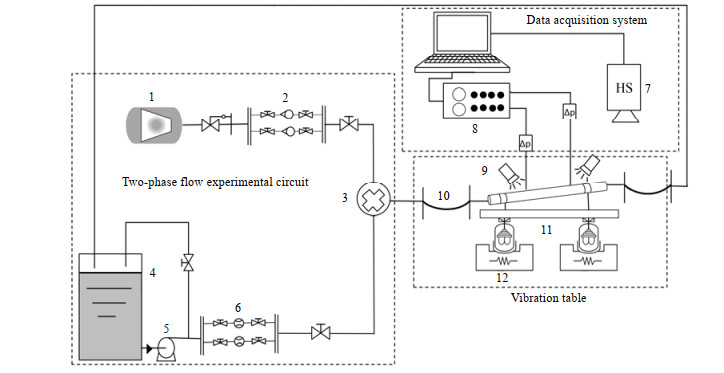
2 实验装置及原理实验装置如图 1所示。将稳态两相流实验回路与振动装置结合,对非线性振动工况下倾斜通道内气液两相流进行研究分析。将直径为35 mm、长度为2 m的透明有机玻璃管倾斜固定于如图 2所示的振动台上。实验在常温常压下进行,通道在水平方向随振动台按正弦规律
|
图 1 实验回路示意图 Fig.1 Schematic diagram of experimental apparatus 1. air compressor 2. orifice flowmeter 3. phase mixer 4. water tank 5. centrifugal pump 6. electromagnetic flow meter 7. high-speed camera 8. differential pressure transmitter 9.fluorescent lamp 10. hose 11.experimental section 12.electromagnetic vibration device |
|
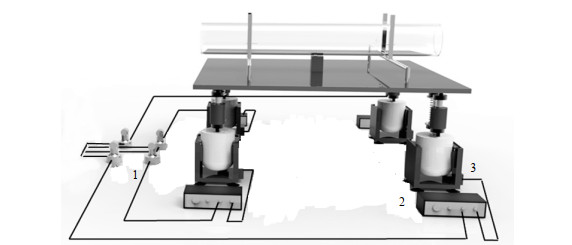
图 2 振动装置示意图 Fig.2 Schematic diagram of vibration configuration 1. capacitance transducer 2. digital switching power amplifier 3. electromagnetism oscillator |
受仪表精度影响,根据间接测量中不确定度的传递规则可得:液相电磁流量计的相对不确定度为0.2%,气相质量流量计测量的相对不确定度为0.5%,压力测量的相对不确定度为0.5%。
3 实验结果与讨论 3.1 振动参数对流型转换界限的影响非稳态振动对流型转换界限的影响与具体工况参数有关。因此,为探讨相关振动参数及倾角对气液相分布的影响,该部分以4种流型为例,针对振动参数及倾斜角度对流型转换界限的影响分别进行探讨与分析。
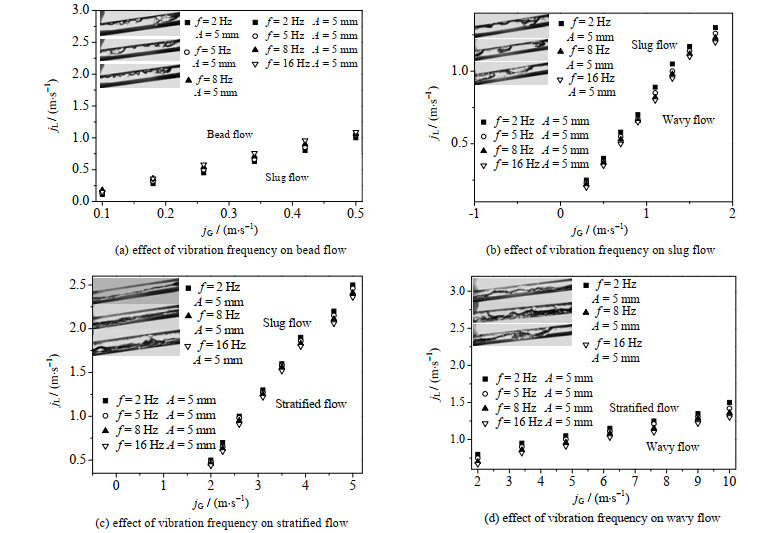
3.1.1 振动频率对流型转换界限的影响以A=5 mm,θ=10°的实验参数为例,针对f=2、5、8及16 Hz工况下倾斜通道内气液两相流动情况进行实验研究,通过高速摄影仪所记录的流型绘制如图 3所示的转换界限图。图 3(a)~(d)分别给出了振动频率对珠状流、弹状流、分层流及波状流的影响,图中jL和jG分别为液相和气相表观流速。
|
图 3 振动频率对流型转换界限的影响 Fig.3 Effect of vibration frequency on flow regime transition |
从图中可知,当振动频率由2增大至16 Hz时,弹状流与珠状流转换界限上移15%左右,与波状流转换界限下移25%左右,与分层流转换界限没有明显差异。同时,由图 3(c)和(d)可知,分层流区域几乎不变。观察不同振动参数下各流型气液相分布特性可发现,虽然振动频率对流型转换界限及气液相界面波动程度有一定影响,但各流型的整体分布趋势没有明显变化。分析如下:
由于分层流具有较高的气液相流速,削弱了振动对其流动的影响,从而只影响了气液相界面波动程度,并未发生流型转变。与之相比,对于珠状流及弹状流,振动频率的改变增大了气液相间的对流作用,使得气泡间产生更强烈的碰撞,气泡密度及尺寸等特性随之发生改变,从而使得弥散的小气泡聚集。这也与GANG等[25]所得结论一致。因此,弹状流区域增大,分层流区域没有明显变化。
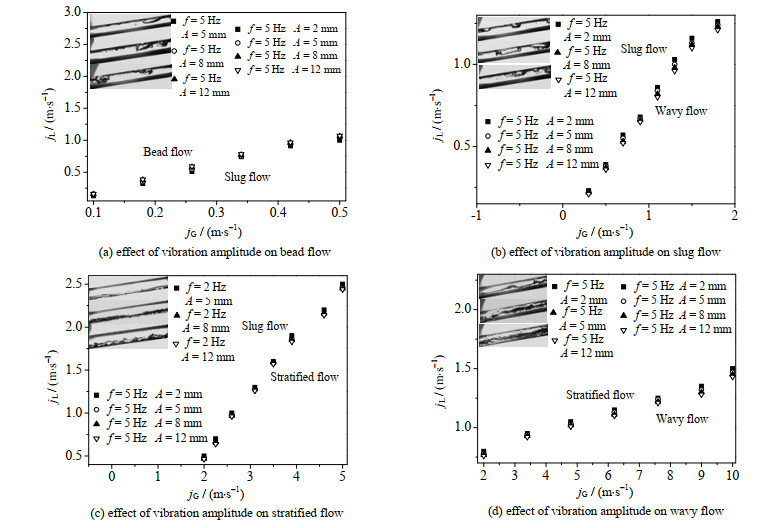
3.1.2 振动幅度对流型转换界限的影响以f=5 Hz,θ=10°的实验参数为例,针对A=2、5、8及12 mm工况下通道内气液两相流动情况进行实验,通过高速摄影仪所得流型绘制如图 4所示的流型转换界限图。图 4(a)~(d)分别给出了振动幅度对珠状流、弹状流、分层流及波状流的影响。
|
图 4 振动幅度对流型转换界限的影响 Fig.4 Effect of vibration amplitude on flow regime transition |
从图 4可知,当振动幅度由2增大至12 mm时,弹状流与珠状流转换界限上移10%左右,与波状流转换界限下移15%左右,与分层流转换界限下移5%左右,分层流与波状流转化界限没有明显变化。与振动频率相比,虽然振动幅度对流型转换界限没有显著影响,但其同样是影响非线性振动通道内气液两相流动特性的重要参数之一。原因如下:
增大振动幅度代表在相同的时间内,实验段会达到更高的幅值,同样可以起到强化对流作用的效果,从而影响气液相界面分布情况。由图 4可知,在相同流动条件下,振动幅度的改变很大程度上影响了液面波动高度,即截面含气率。这也验证了文献[26]所得结论:当振动幅度较大时,圆管内流体沿半径方向分布的速度不再符合泊松分布,而是呈现“速度环”效应,且最大速度出现在圆管壁面附近。
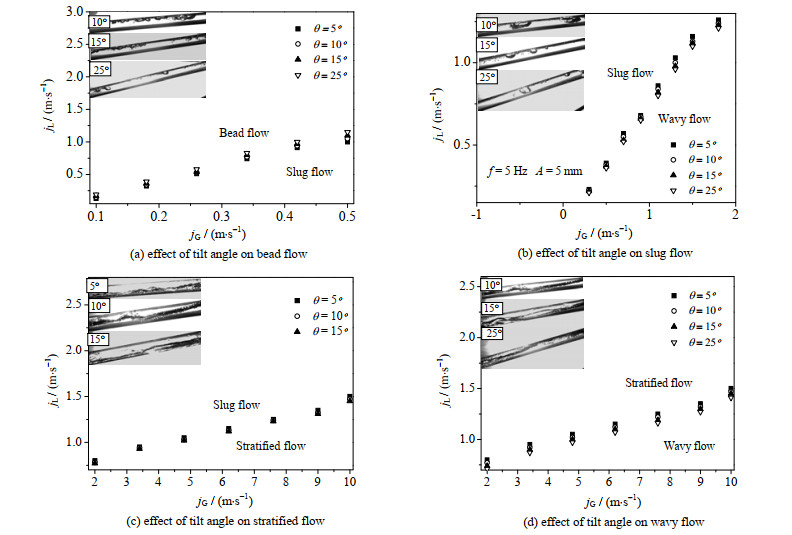
3.1.3 倾斜角度对流型转换界限的影响以f=5 Hz,A=5 mm的实验参数为例,针对θ=5°、10°、15°及25°工况下通道内气液两相流动情况进行实验,通过高速摄影仪所得流型绘制如图 5所示的流型转换界限图。图 5(a)~(d)分别给出了倾角对珠状流、弹状流、分层流及波状流的影响。
|
图 5 倾斜角度对流型转换界限的影响 Fig.5 Effect of inclination angle on flow regime transition |
从图中可知,当通道倾斜角度由5°增大至25°时,分层流与波状流转换界限下移10%左右,其他各流型间转换界限无明显差异。然而由图 5(c)可知,当倾角为25°时,原有流动条件下并未出现分层流。且通过观察珠状流及弹状流气泡形状可发现,倾角越大,气泡不规则度越高。分析如下:
倾角改变使气泡所受浮力及振动附加力在轴向上的分力发生变化,相应改变了气泡形状,然而气泡的稳定程度主要受振动参数的影响,因此引起其流型发生改变。对于分层流和气相流速较大的波状流,倾角增大会引起液相呈现倒流趋势,受增大的重力及振动附加力的影响,分层流及稳定的波状流在θ=25°的管道内很难形成。
如表 1所示为流型转换界限数值。由表可知,振动参数及倾斜角度越大,通道内气液相分布越复杂。振动幅度主要影响液面的波动高度,振动频率主要影响液面波动的激烈程度,倾斜角度则主要影响气泡形状及液面波动角度。由此可说明,倾斜通道内气液两相流动受振动参数及倾斜角度的综合影响,振动越剧烈,原有流场所受的影响越强,流线偏离原流动方向的程度越大。
|
|
表 1 流型转换界限数值 Table 1 Data of flow regime transition |
由3.1.1节及3.1.2节的气液相分布情况所得结论可知,振动参数的改变会相应影响通道内截面空隙率。因此,该部分对稳态及动态工况下的空隙率进行测量,同时利用文献中各经验公式计算其平均空隙率,并将结果与测量值进行了对比。
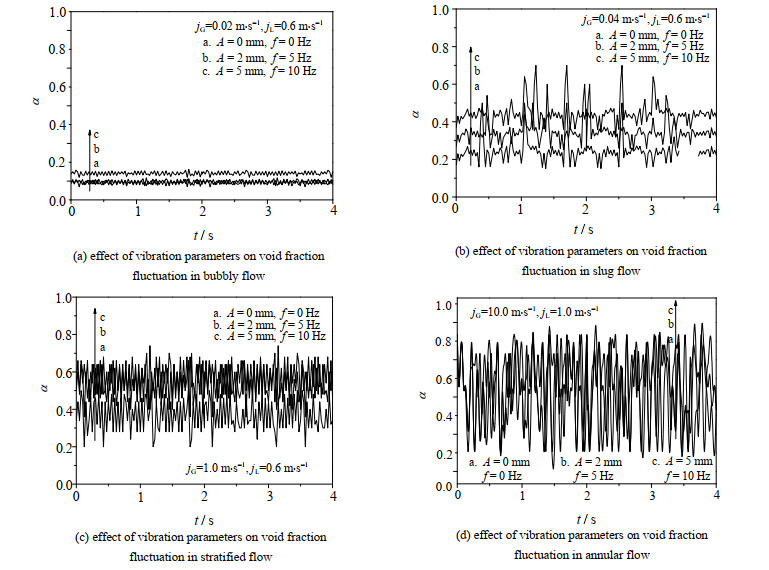
3.2.1 振动参数对瞬时空隙率的影响以θ=10°的实验参数为例,通过光纤探针技术对稳态及动态工况下通道内空隙率进行测量,图 6(a)~(d)分别给出了泡状流、弹状流、分层流及环状流的空隙率波动趋势。图中t为时间,α为空隙率。
|
图 6 振动对瞬时空隙率的影响 Fig.6 Effect of vibration on instantaneous void fraction |
从图中可知,泡状流和环状流的空隙率受振动参数影响不大。与之相比,弹状流空隙率分布出现了明显的波动趋势,其峰值出现的周期性也可反映出气泡出现的时间点。对于分层流,振动参数的改变对其波动规律没有明显影响,但显著减小了其空隙率均值。分析如下:
一般情况下,空隙率是气液两相质量分数的函数,与两相的密度、动态黏度等物理性质有关。然而,根据文献[27]所得结论可知,空隙率不仅与两相质量分数之比密切相关,而且受液相速度影响。由3.1.1节及3.1.2节所示的流型图可知,非线性振动对通道内气液相分布有显著影响,相应也会影响液体流量。因此,动态工况下通道内的空隙率均值较大。
3.2.2 平均空隙率的计算由3.1节可知,振动参数及通道倾角均会影响通道内流体气液相分布情况,因此,该部分以几种典型振动工况及倾角为例,对不同实验工况下通道内平均空隙率进行了计算与测量。
对于稳态工况下通道内两相流体的空隙率,已有大量专家学者对其进行了研究和验证,以期更好地分析其变化规律。通过大量对比计算,AHN等[28]发现以气液两相流型为基础所提出的计算模型可以更准确地预测通道内的空隙率。根据不同流型,其关联式表示如下:
对于泡状流及弹状流,
| $\alpha=0.158\left(\frac{j_{\mathrm{G}}}{j_{\mathrm{L}}}\right)\left(\frac{1}{F r_{\mathrm{L}}^{0.5}}\right) $ | (3) |
| $\alpha=0.302\left(\frac{j_{\mathrm{G}}}{j_{\mathrm{L}}}\right)^{0.2}\left(\frac{1}{F r_{\mathrm{L}}^{0.1}}\right)$ | (4) |
式中:FrL为HART等[29]通过引入通道倾斜角度θ得出的液相Froude数,其定义为
| $F_{\mathrm{L}}=\frac{\rho_{\mathrm{L}} j_{\mathrm{L}}^{2}}{g\left(\rho_{\mathrm{L}}-\rho_{\mathrm{G}}\right) D_{\mathrm{h}} \cos \theta}$ | (5) |
式中:g为重力加速度,ρL和ρG分别为液相和气相的密度,Dh为通道当量直径。
对于分层流及波状流,BIBERG[30]提出如下关联式:
| $\alpha=\left\{1+\frac{j_{\mathrm{L}}}{j_{\mathrm{G}}}\left[1+\left(108 R e_{\mathrm{L}}^{-0.726} \frac{\rho_{\mathrm{L}}}{\rho_{\mathrm{G}}}\right)\right]^{0.5}\right\}^{-1}$ | (6) |
式中:ReL为液相雷诺数。
对于环状流,AHN等[28]通过测量液膜厚度δ来预测空隙率:
| $\alpha=\left(1-2 \delta / D_{\mathrm{h}}\right)^{2}$ | (7) |
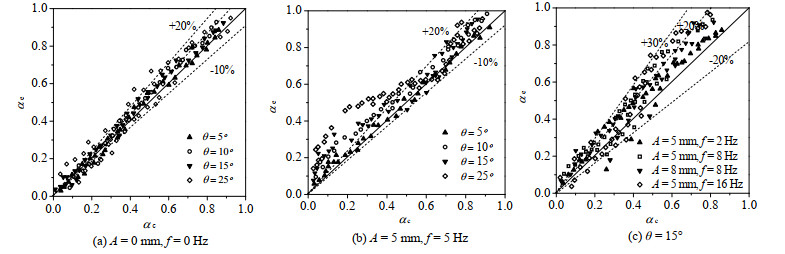
通过各经验公式获得的平均空隙率值与实验值的对比如图 7所示,其中图 7(a)与图 7(b)分别为稳态工况与振动工况下不同倾角通道内空隙率比较值,图 7(c)显示了通道内空隙率的计算值与测量值在不同振动参数下的偏差程度,其中αc为空隙率的计算值,αe为空隙率的测量值。
|
图 7 倾斜通道内空隙率计算结果比较 Fig.7 Comparison of calculated and experimental results of void fraction in inclined channel |
如图 7(a)和(b)所示,稳态工况下不同倾角通道内空隙率的理论值相对于测量值的误差基本在10%以内。与之相比,振动通道内空隙率预测值相对于测量值的误差较大,特别是泡状流及弹状流区域,且倾角对其有显著影响,倾角越大其误差越明显。但对于不同倾角通道内的波状流及环状流,其测量误差基本在20%以内。由图 7(c)可发现,当倾角为15°时,对比振动频率及幅度对其产生的影响可发现,高振动频率通道内空隙率计算误差达到30%,而高振动幅度通道内其误差在20%以内。由此可以得出,振动频率对通道内气液两相流动影响更明显。
由图 7可知,基于流型提出的稳态工况的空隙率计算模型同样适用于非线性振动工况下倾斜通道的计算,且在低频率小振幅工况下(频率小于2 Hz,振幅小于5 mm),误差可降低至10%以内。
4 结论(1) 非线性振动及倾角影响通道内气液相分布情况,但对流型定义没有明显影响,且振动频率对其影响更加明显。
(2) 振动参数及倾角影响流型转换界限。综合来看,弹状流区域扩张,珠状流转换界限上移10%左右,波状流转换界限下移20%左右,分层流区域没有明显改变。
(3) 振动幅度主要影响液面波动高度,即截面空隙率;而振动频率主要影响液面波动的激烈程度,倾斜角度则主要影响气泡形状及液面波动角度。
(4) 除泡状流和环状流外,与稳定工况下空隙率波动幅值和均值相比,各流型在非线性振动状态下其值均明显增大。
基于流型提出的稳态工况下空隙率计算模型同样适用于非线性振动工况下倾斜通道的计算,且在频率小于2 Hz,振幅小于5 mm的低频率小振幅工况下,误差可降低至10%以内。
| [1] |
HUMPHRIES J R, DAVIES D. A floating desalination/co-generation system using the KLT-40 reactor and Canadian RO desalination technology[R]. Vienna: International Atomic Energy Agency, 1998.
|
| [2] |
PANOV Y K, POLUNICHEV V I, ZVEREV K V. Nuclear floating power desalination complexes[R]. Vienna: International Atomic Energy Agency, 1998.
|
| [3] |
刘国强, 孙立成, 阎昌琪. 竖直圆管内泡状流界面参数分布特性[J]. 原子能科学技术, 2014, 48(7): 1176-1181. LIU G Q, SUN L C, YAN C Q. Interfacial parameter distribution of bubbly flow in vertical circular tube[J]. Atomic Energy Science and Technology, 2014, 48(7): 1176-1181. |
| [4] |
ISHIDA T, YORITSUNE T. Effects of ship motions on natural circulation of deep sea research reactor DRX[J]. Nuclear Engineering and Design, 2002, 215(1/2): 51-67. |
| [5] |
峦峰, 阎昌琪. 摇摆状态下水平管内气-水两相流的流型研究[J]. 核动力工程, 2007, 28(2): 19-23. LUAN F, YAN C Q. Study on the flow pattern of gas water two phase flow in a horizontal pipe in a swing state[J]. Nuclear Power Engineering, 2007, 28(2): 19-23. |
| [6] |
TAN S C, WANG Z W, Chang W, et al. Flow fluctuations and flow friction characteristics of vertical narrow rectangular channel under rolling motion conditions[J]. Experimental Thermal and Fluid Science, 2013, 50: 69-78. DOI:10.1016/j.expthermflusci.2013.05.006 |
| [7] |
CHEN S W, LIU Y, HINIKI T. Experimental study of air-water two-phase flow in an 8×8 rod bundle under pool condition for one-dimensional drift-flux analysis[J]. International Journal of Heat and Fluid Flow, 2012, 33(1): 168-181. DOI:10.1016/j.ijheatfluidflow.2011.09.012 |
| [8] |
陈冲, 高濮珍. 摇摆工况下窄矩形通道内两相沸腾摩擦压降特性[J]. 化工学报, 2015, 66(2): 3874-3880. CHEN C, GAO P Z. Frictional pressure drop characteristics of two phase boiling in narrow rectangular channel under swing condition[J]. CIESC Journal, 2015, 66(2): 3874-3880. |
| [9] |
TALLEY J D, WOROSZ T, KIM S. Characterization of horizontal air-water two-phase flow in a round pipe partⅡ:Measurement of local two-phase parameters in bubbly flow[J]. International Journal of Multiphase Flow, 2015, 76: 223-236. DOI:10.1016/j.ijmultiphaseflow.2015.06.012 |
| [10] |
CATALINA P, PAILO W. Effect of forced flow oscillations on churn and annular flow in a long vertical tube[J]. Experimental Thermal and Fluid Science, 2017, 81: 345-357. DOI:10.1016/j.expthermflusci.2016.10.015 |
| [11] |
贾辉, 谭思超, 高濮珍. 不稳定条件下水平管单相水流动阻力特性实验研究[J]. 原子能科学技术, 2011, 45(2): 168-173. JIA H, TAN S C, GAO P Z. Experimental study on horizontal single phase water flow resistance characteristics under unsteady flow condition[J]. Atomic Energy Science and Technology, 2011, 45(2): 468-173. |
| [12] |
周世忠, 朱琳, 张阳波. 大流量下倾斜管内气液两相流实验研究[J]. 当代化工, 2016, 45(3): 504-506. ZHOU S Z, ZHU L, ZHANG Y B. Experimental study of two-phase flow in inclined pipe under high gas-liquid flow[J]. Contemporary Chemical Industry, 2016, 45(3): 504-506. |
| [13] |
张金红, 阎昌琪, 方红宇. 摇摆对水平管内气液两相流型的影响[J]. 核科学与工程, 2007, 27(3): 206-212. ZHANG J H, YAN C Q, FANG H Y. Effects of rolling on gas-water two-phase flow in horizontal pipes[J]. Chinese journal of Nuclear Science and Engineering, 2007, 27(3): 206-212. |
| [14] |
曹夏昕, 阎昌琪, 孙立成. 摇摆状态下竖直管内单相水阻力特性实验研究[J]. 核动力工程, 2007, 28(3): 51-55. CAO X X, YAN C Q, SUN L C. Pressure drop characteristics of single-phase flow in vertical rolling pipes[J]. Nuclear Power Engineering, 2007, 28(3): 51-55. |
| [15] |
周云龙, 尹洪梅, 丁会晓. 多尺度熵在棒束通道气液两相流压差信号分析中的应用[J]. 化工学报, 2016, 67(9): 3625-3632. ZHOU Y L, YIN H M, DING H X. Application of multi-scale entropy in analyzing pressure difference signals of gas-liquid two-phase flow in rod bundled channel[J]. CIESC Journal, 2016, 67(9): 3625-3632. |
| [16] |
丁浩, 黄志尧, 李海青. 气液两相流压差波动的Hilbert-Huang变换特性[J]. 化工学报, 2005, 56(12): 2294-2302. DING H, HUANG Z Y, LI H Q. Property of differential pressure fluctuation signal of gas-liquid two-phase flow based on Hilbert-Huang transform[J]. CIESC Journal, 2005, 56(12): 2294-2302. |
| [17] |
CHISHOLM D. A theoretical basis for the Lockhart-Martinelli correlation for two-phase flow[J]. International Journal of Heat and Mass Transfer, 1967, 10: 1767-1778. DOI:10.1016/0017-9310(67)90047-6 |
| [18] |
PENDAYALA R, JAYATIN S, BALKRISHINAN A R. Convective heat transfer in single-phase flow in a vertical tube to axial low frequency oscillations[J]. Heat Mass Transfer, 2008, 44: 857-864. DOI:10.1007/s00231-007-0302-3 |
| [19] |
PENDAYALA R, JAYATIN S, BALKRISHINAN A R. Flow and pressure drop fluctuations in vertical tube subject to low frequency oscillations[J]. Nuclear Engineering and Design, 2008, 238(1): 178-187. |
| [20] |
JING G, YAN C, SUN L. Void fraction of dispersed bubbly flow in a narrow rectangular channel under rolling conditions[J]. Progress in Nuclear Energy, 2014, 7(1): 256-265. |
| [21] |
BARNEA D, SHOHAM O, TATEL Y. Gas-liquid flow in inclined tubes with the flow pattern transitions for upward flow[J]. Chemical Engineering Science, 1985, 45(1): 131-136. |
| [22] |
CHEN S W, HIBIKI T, ISHIMI M. Experimental study of adiabatic two-phase flow parameter in an annular channel under low-frequency vibration[J]. Journal of Engineering for Gas Turbines and Powers, 2014, 136: 032501. DOI:10.1115/1.4025726 |
| [23] |
周云龙, 赵盘, 杨宁. 振动状态下水平管内气液两相流流型转变的实验研究[J]. 热能动力工程, 2017, 32(6): 17-22. ZHOU Y L, ZHAO P, YANG N. Experimental study on flow pattern transition of gas liquid two-phase in horizontal tubes under vibration condition[J]. Journal of Engineering for Thermal Energy and Power, 2017, 32(6): 17-22. |
| [24] |
周云龙, 李珊珊. 起伏振动状态下倾斜管内两相流多尺度熵分析[J]. 化工学报, 2018, 69(5): 1884-1891. ZHOU Y L, LI S S. Multi-scale entropy analysis of two-phase flow in inclined pipe under vibration condition[J]. CIESC Journal, 2018, 69(5): 1884-1891. |
| [25] |
GANG H, XIAO Y. Experimental research of bubble characteristics in narrow rectangular channel under heaving motion[J]. International Journal of Thermal Sciences, 2012, 51: 42-50. DOI:10.1016/j.ijthermalsci.2011.08.010 |
| [26] |
刘建华, 王宏光, 韩铁鹰. 管内壁面振动对流场与传热影响的模拟研究[J]. 热能动力工程, 2017, 32: 14-20. LIU J H, WANG H G, HAN T Y. Numerical study of the influences of wall vibration on the flow and heat exchange in tube[J]. Journal of Engineering for Thermal Energy and Power, 2017, 32: 14-20. |
| [27] |
OKAWA T, GOTO T, YAMAGOE Y. Liquid film behavior in annular two-phase flow oscillation conditions[J]. International Journal of Heat and Mass Transfer, 2010, 53: 962-971. DOI:10.1016/j.ijheatmasstransfer.2009.11.024 |
| [28] |
AHN T H, YUN B J, JEONG J J. Void Fraction prediction for separated flows in the nearly horizontal tubes[J]. Nuclear Engineering Technology, 2015, 47: 669-677. DOI:10.1016/j.net.2015.06.005 |
| [29] |
HART J, HAMERSMA P J, FORTUIN J M H. Correlations predicting frictional pressure drop and liquid holdup during horizontal gas-liquid pipe flow with a small liquid holdup[J]. International Journal of Multiphase Flow, 1989, 15: 947-964. DOI:10.1016/0301-9322(89)90023-2 |
| [30] |
BIBERG D. An explicit approximation for the wetted angle in two-phase stratified pipe flow[J]. Canada Journal of Chemical Engineering, 1999, 77: 1221-1224. DOI:10.1002/cjce.5450770619 |




