多喷嘴水煤浆气化炉由燃烧室和洗涤冷却室组成,气化燃烧室出来的高温粗合成气,通过洗涤冷却管进入位于气化炉下部的洗涤冷却室,在与冷却水直接接触传递下,粗合成气的温度急剧下降,部分液相水蒸发进入气相,使离开洗涤冷却室的工艺气得以增湿,以此来满足后续工段的工艺要求[1]。冷却水通过冷却水分布环在洗涤冷却管内壁形成一定厚度的激冷水膜,高温合成气与水膜接触过程中发生剧烈的热质传递,若水膜发生断裂,不但会降低液膜的冷却作用,更会使洗涤冷却管内壁直接与高温合成气接触,使其承受高温而产生变形甚至烧损,因此对洗涤冷却管内壁的降膜流动特性的研究具有重要意义。王灵萍等[2]对经洗涤冷却环分布形成的下降管内壁垂直降膜的厚度的空间分布进行了研究。实验发现3 mm的洗涤冷却环的液膜均布性最佳。王晶[3]、颜留成等[4]对不同雷诺数下的液膜厚度进行了测定,发现液相雷诺数有一临界值,在临界值两侧液膜厚度的变化趋势相反。Yu Y Q等[5]利用电容探头及高速摄像研究了平板上的垂直降膜流动特性,Tihon J[6]则利用探头和传感器测量了液膜厚度和壁面剪切力随时间的变化规律。Alekseenko S V[7]对在气体顺流和逆流下降膜表面产生的线性波的参数作了二维研究,液体和气体雷诺数范围分别为0~8000和24~125。Nowak M[8]采用脉冲超声波测速技术研究了管内的湍流边界层。Zhou D W[9]对平板降膜的瞬时和统计特性进行测量,建立了新的平均液膜厚度关系式,Dupont J[10]对平板上湍流降膜的厚度作二维映射,而Moran-K[11]则利用可视化手段研究了倾斜平板上的层流降膜流动。余黎明等[12]采用激光多普勒测量了不同气液流动条件下的降膜流动的液相速度分布和瞬时速度波动。Gurau B等[13]利用双传感器热膜风速仪探针发出的互相关信号来测量气液在水中和在空气-水的两相流中的局部速度。Drosos等[14]对矩形竖直管中的发展自由降膜进行了研究,实验测量了三种不同液体:水、浓度1.5%的丁醇和2.5%的丁醇,通过可视化技术发现较小的表面张力会影响进口区域的波的初始段。Kostoglou M[15, 16]实验研究发现,当液膜雷诺数Rel < 3000时,液膜中大波的分布呈随机性,当Rel > 5000时观察到了波之间的相互排斥,且新的大波会在低于液膜平均厚度的波中产生。Karimi G[17]测量了在气体顺流和逆流情况下,波动液膜的瞬时速度和膜厚等。大部分对于液膜的实验研究及理论模型均为层流或者液膜雷诺数Rel较低的中低度湍流且对于气相影响下的液膜实验较少,而在洗涤冷却管中液膜的湍动程度远高于此同时液膜流动也受到合成气的影响。
本文借助超声多普勒测速仪[18, 19](ultrasound Doppler velocimetry, UDV),研究在气相剪切作用下降膜流动行为影响规律,测量了洗涤冷却管内高液膜雷诺数下垂直降膜的液膜流动厚度与速度,研究其分布特性,为降膜流动在洗涤冷却室内的应用提供理论指导。
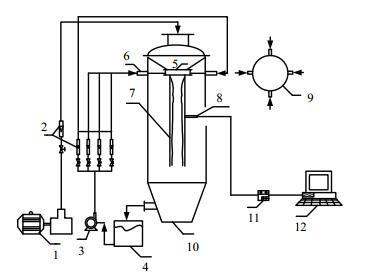
2 实验装置和方法 2.1 实验装置实验的装置流程如图 1所示,装置中激冷环材质为不锈钢,其余洗涤冷却室、洗涤冷却管等为有机玻璃。其中洗涤冷却管高度为1 m,内径为0.138 m。实验介质液相为水,气相为空气。水由水泵输送至洗涤冷却环,洗涤冷却环上共有四个对称的入水口,控制每个入水口进水流量相同。冷却水经洗涤冷却环的分配,沿洗涤冷却管的内壁呈降膜流动。实验主要测量在不同气相雷诺数下,洗涤冷却管不同周向和轴向位置的液膜的厚度和流速分布,研究影响管中降膜流动的敏感参数。
|
图 1 装置流程图 Fig.1 Schematic diagram of the experimental setup 1. blower 2. flowmeter 3. water pump 4. water tank 5. scrubbing cooling ring 6. water inlet 7. scrubbing cooling tube 8. transducer 9. top view of the ring 10. chamber 11. UDV 12. computer |
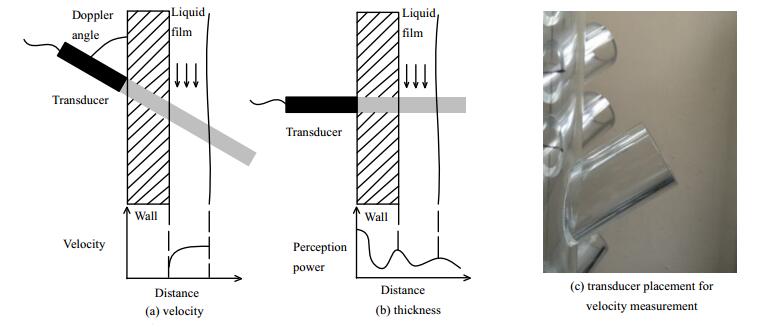
实验采用超声多普勒流速测量系统(UDV)并配合探针传感器进行液膜厚度和流速的测量,测量原理如图 2。
超声波探头向待测流体发出一定频率的超声波,当超声波传播方向与流体方向成一定夹角(即多普勒角),遇到介质中的固体颗粒、气泡等示踪粒子时,反射波的频率会发生改变,探头接收到不同深度粒子反射波的时间不同,可得到超声波发射方向上不同深度的流体速度,如图 2(a),当仪器发出的超声波在穿过两相界面时会有较强的反射,在固—液界面和气—液界面所反映的信号均会出现峰值,如图 2(b),两个较强反射信号峰之间的距离即为液膜的厚度。实验所采用的传感器直径8 mm,探测区域直径为5 mm,所发出的超声波频率为4 MHz,采样速度为每秒100组数据,超声波传播方向上空间分辨率最低为0.12 mm。
|
图 2 超声多普勒流速和膜厚测量原理 Fig.2 Velocity and thickness measurement of liquid films by ultrasonic Doppler velocimetry |
因实验装置中心对称,故测量时只在0~45°选择测量点。厚度测量选取了0,8,16,24,34.5与45°六个周向位置,每个位置在0~1 m的轴向上14个测量点。速度测量由于放置探针的装置空间尺寸问题选取0,22.5与45°三个周向位置,如图 2(c),同样每个位置轴向上共取13个测量点。洗涤冷却环出口处液膜平均速度范围为1.76 m·s-1,而液膜沿壁面向下流动的情况,通常用无量纲数来定义其流动特性:Rel(液膜雷诺数),其计算式为Rel = 4Γ/μ,Γ为单位湿周上的质量流量。
据液膜流动的实验观察表明,降膜流动一般分为三种情况[20]:当Rel ≤ 20时,流动为层流,液膜表面为平滑态;当20 ≤ Rel ≤ 2000时,流动呈波动的层流;当Rel ≥ 2000时流动为剧烈波动的湍流。本实验中Rel = 2.04×104,因此管内液膜处于高度湍流阶段。气相流量取0,200,400 m3·h-1,所对应流速为0,3.71,7.43 m·s-1,气相雷诺数Reg为0,3.81×104,6.83×104。激冷环槽缝宽度为3和5 mm。实验操作工况如表 1所示:
|
|
表 1 实验工况 Table 1 Experimental conditions |
UDV测得液膜的瞬时厚度δ,其重复测量的标准不确定度即实验标准偏差SD (δ),为:
| $ {\rm{SD}}\left( \delta \right){\rm{ = }}\sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{\delta _i} - \overline \delta } \right)}^2}} }}{{n - 1}}} $ | (1) |
UDV测量液膜厚度的仪器误差Δδ = 0.06 mm,假设测量为均匀分布,取包含因子k =
| ${U_{\Delta \delta }} = \frac{{\Delta \delta }}{{\sqrt 3 }}$ | (2) |
则液膜厚度的相对不确定度为:
| $\frac{{{U_\delta }}}{\delta }{\rm{ = }}\sqrt {{\rm{SD}}{^2}\left( \delta \right) + U_{\Delta \delta }^2} $ | (3) |
本实验条件下,液膜厚度的相对不确定度最大值约为12.6%,同理可得流速的相对不确定度最大值为12.3%。
3 实验结果讨论 3.1 液膜厚度分析实验对气相影响下液膜的厚度进行了测量,实验液膜雷诺数Rel为2.04×104,Reg气相雷诺数范围0~6.83×104,选取的洗涤冷却环的槽缝宽度为3和5 mm,所得结果如下:
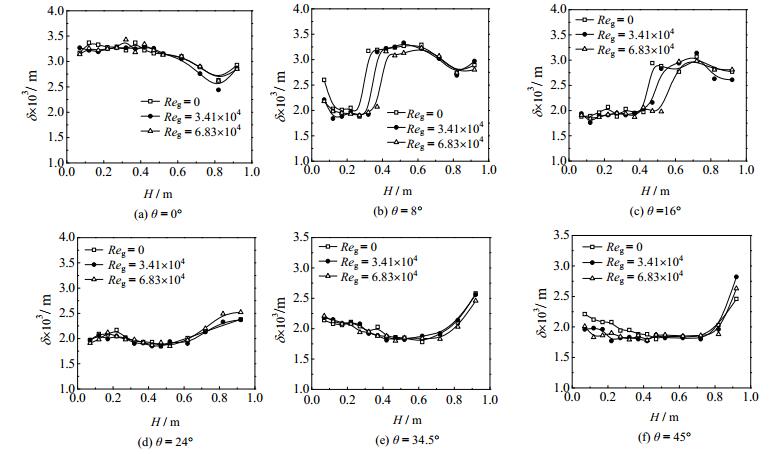
洗涤冷却环槽缝宽度为3 mm时,无气体通入和不同气相雷诺数下各周向角及轴向上液膜厚度的变化情况如图 3所示。
|
图 3 3 mm槽缝宽度下不同气相雷诺数下液膜轴向厚度分布 Fig.3 Axial distribution of liquid film thickness at different Reg (3 mm slot) |
由图 3(a)可见,在周向位置0°处,气相雷诺数对液膜厚度的变化的影响不显著,不同气相雷诺数下膜厚均沿轴线距离增大缓慢减小。此外,在相同轴向位置,液膜平均厚度最大值与最小值最大相差约7%,差距较小。在3(b)周向8°处,可以明显的看到在H = 0.2~0.4 m,8°的液膜厚度有个明显的增大趋势,且随着气相雷诺数的增大,膜厚开始增大的轴向位置随之延后。由于气液两相并流流动,随着气相雷诺数的增大,空气对液膜表面的剪切力也在增大,加快了液膜表面的流动进程,而液膜在横向均布扩散的运动较慢,因此气相使得液膜原本开始向两边扩散的位置向下移动。
在图 3(c)中的周向16°处也可以看到类似的液膜厚度延后增大的情况,在H = 0.4 ~0.55 m,膜厚增加根据气相雷诺数不同出现了相应程度的延后,气相雷诺数越大,延后程度越大。而之后(d)~(f)的周向角24、34.5、45°三个周向位置液膜平均厚度变化趋势非常接近,均无此现象的出现,在此范围中,气相雷诺数对平均膜厚基本没有影响,而由于该处周向角距入水口较远,液膜扩散所带来的膜厚增加是较为平缓的。此外,从图 3也可以看出除了0°位置的膜厚在竖直流动过程中呈现略微下降趋势,其余各角度均存在膜厚增大的情况,轴向角8°的液膜出现厚度增加最早,大致在H = 0.3 m左右,45°最晚,约为H = 0.8 m时才发生。
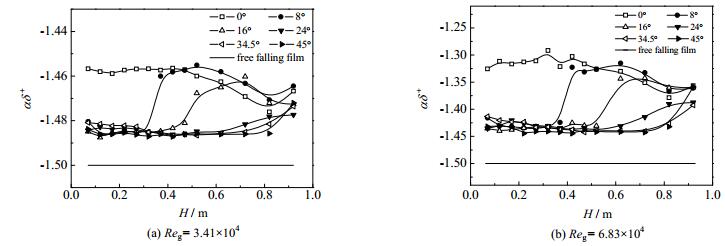
为进一步验证实验的可信度及液膜厚度的变化趋势,引入参数αδ+[21]用以衡量界面剪切的影响,其定义如下:
| $ \alpha {\delta ^{\rm{ + }}}{\rm{ = }} - \frac{{\tilde g\delta }}{{{u^{{ * ^2}}}}} $ | (4) |
| $ \tilde g{\rm{ = }}\frac{1}{{{\rho _l}}}\left| {\frac{{{\rm{d}}p}}{{{\rm{d}}z}}} \right| + g $ | (5) |
| $ {u^ * } = \sqrt {\frac{{{\tau _{\rm{c}}}}}{{{\rho _l}}}} $ | (6) |
其中u*为剪应力速度,
|
图 4 αδ+在不同气相雷诺数下下的轴向变化 Fig.4 Axial variatom of αδ+ at different Reg |
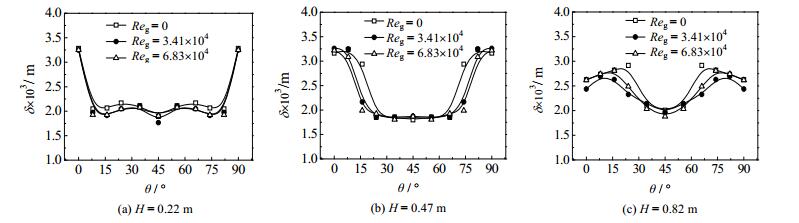
图 5给出了3 mm槽缝宽度的洗涤冷却环在各个周向角上液膜平均厚度分布,选取了H = 0.22、0.47和0.82 m三个轴向位置。由图可见,0°周向处在不同气相雷诺数下液膜平均厚度远大于其余周向,液膜厚度从初始段开始,因为中央液膜在流动过程中不断向两边周向扩散而逐渐降低。
|
图 5 3 mm槽缝宽度下不同气相雷诺数下液膜周向厚度分布 Fig.5 Circumferential distribution of liquid film mean thickness at different Reg (3 mm slot) |
周向8和16°处的平均液膜厚度总体趋势均从初始较薄的膜厚经中央液膜的两侧铺展后增大,且在洗涤冷却管中下段(H≥0.47 m)受气相雷诺数影响明显。而在24、34.5、45°周向上液膜厚度受气相雷诺数变化很小,随着流动距离的增加,受中间液膜的铺展而使厚度略微增加。
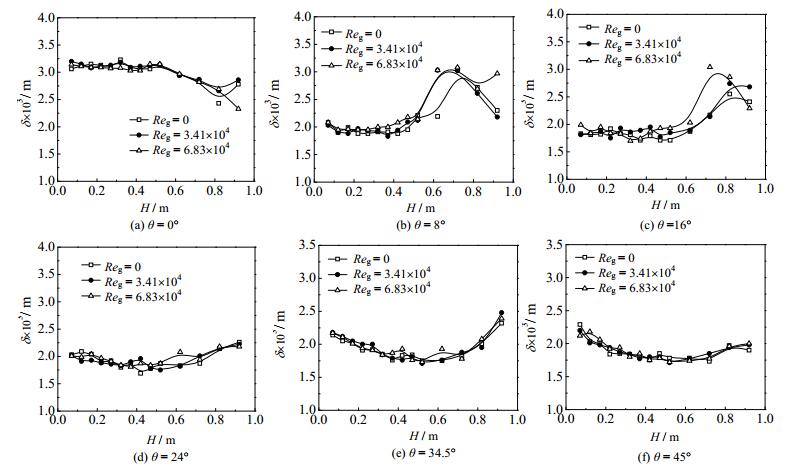
图 6为洗涤冷却环的槽缝宽度为5 mm时,不同气相雷诺数下洗涤冷却管内各周向液膜的分布情况,可以看到在0、24、34.5、45°周向角上液膜厚度变化与3 mm槽缝时相似。液膜在0°周向角的厚度由于入水口原因依旧在各周向角的膜厚中处于最大。24、34.5、45°这三个周向角的液膜厚度变化趋势类似,在H≈0.05 m的初始段由于刚从洗涤冷却环中流出,受到空间局限,液膜并未铺展开,因此该处液膜厚度较大,而随着流动距离增加,液膜受重力作用流速逐渐增大因而膜厚逐渐变薄,最后在H = 0.7~0.8 m处受中央液膜向两侧铺展的影响,厚度呈增大趋势。由图 6(b)和(c)可看出,在8和16°处也同样存在与3 mm槽缝宽度下相同的情况。
|
图 6 5 mm槽缝宽度下不同气相雷诺数下液膜轴向厚度分布 Fig.6 Axial distribution of liquid film thickness at different Reg (5 mm slot) |
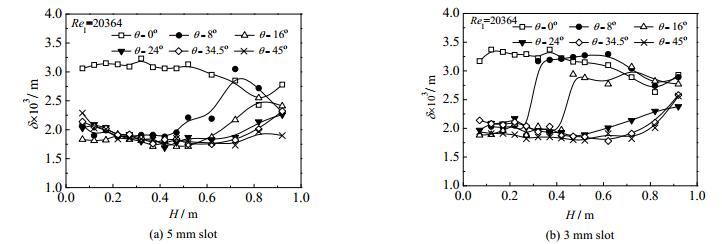
图 7给出了在液相雷诺数为2.04×104时,液相水流经不同槽缝宽度的洗涤冷却环后所形成的平均液膜厚度分布,由图可见,平均液膜厚度范围1.5~3.5 mm,与王灵萍[2]用电导探针所得结果基本一致。此外,除了0°位置的膜厚在竖直流动过程中呈现略微下降趋势,其余各角度均存在一个膜厚开始有较大增幅的轴向位置点,轴向角8°的液膜出现厚度增加最早,45°最晚,这也符合前述的液膜径向均布规律。当槽缝宽度增大为5 mm时,液膜厚度增大的位置有所推迟,其原因是5 mm条件下液膜集聚状况不明显,并没有发生液膜的脱离[3, 4],导致中央液膜向两边扩散的幅度较缓,且在其余几个周向上的液膜厚度增幅也较3 mm小。综上可表明槽缝宽度的增加使得中央液膜向两边扩散的进程大大延后,这导致在初始段除0°外其余周向角液膜厚度均较薄的问题。
|
图 7 不同槽缝液膜厚度发展比较 Fig.7 Comparison of liquid film thickness with different slot width |
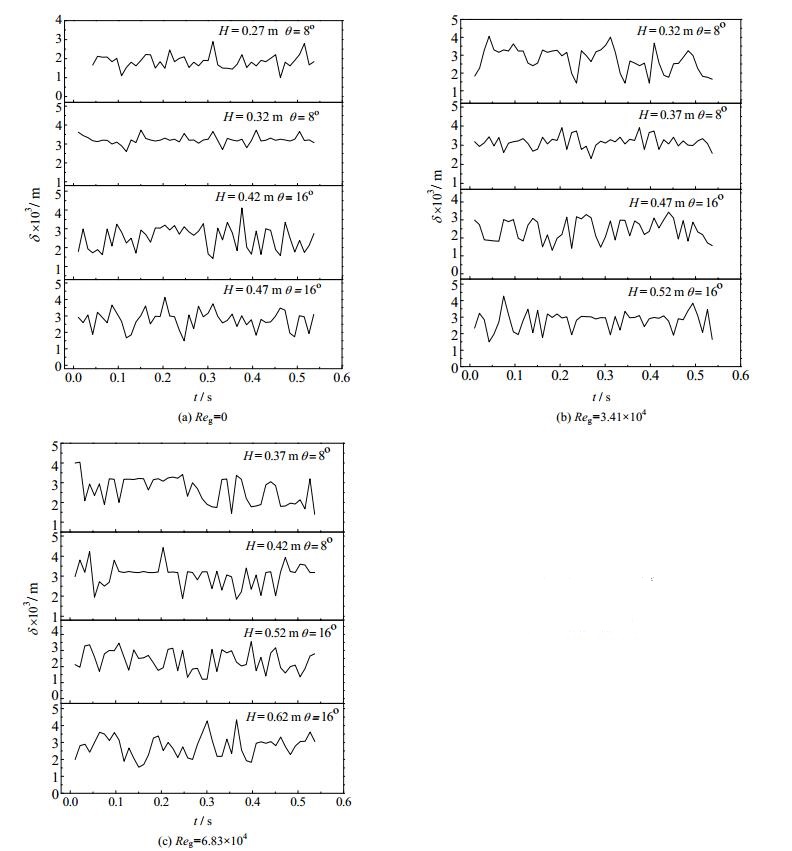
随后,实验对于8和16°这两个特殊位置的液膜厚度波动进行进一步分析,对于这两处发生的液膜增厚延迟的现象,取膜厚变化的前后2处轴向位置进行瞬时膜厚的分析,具体条件和位置如表 2,取样样本为50个,所得液膜厚度波动图如图 8:
|
图 8 膜厚瞬时波动图 Fig.8 Instantaneous fluctuation of film thickness |
|
|
表 2 瞬时膜厚测量位置及条件 Table 2 Location and conditions of instantaneous film thickness measurements |
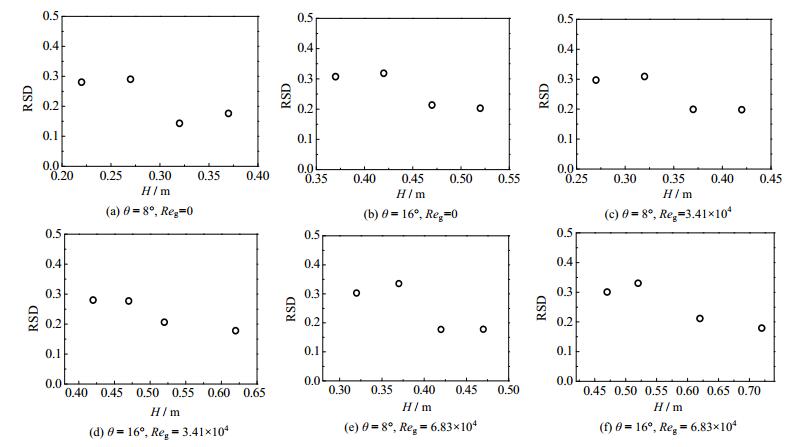
从图 8可以看出,在相同周向角和气相雷诺数条件下,液膜增厚的两处轴向位置的膜厚瞬时变化,在液膜开始增厚时液膜波动明显较结束时更加剧烈,这一变化通过瞬时膜厚的相对标准误差RSD来衡量,如式(7)。同时,在膜厚变化2处轴向位置前后各多取1个点来表明变化趋势。
| $ {\rm{RSD}}{\rm{ = }}\sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{\delta _i} - \overline \delta } \right)}^2}} }}{{(n - 1){{\overline \delta }^2}}}} $ | (7) |
从图 9可看出在两个周向角液膜增厚的轴向位置处的RSD存在明显变化,增厚前液膜的RSD大于之后的轴向位置的RSD表明,在液膜开始增厚处液膜波动剧烈,且这一过程在轴向位置的跨度约0.1~0.15 m,随后液膜波动较之前趋于平缓,该图也侧面证明了在气相流速增大时液膜增厚的轴向位置存在推迟现象。
|
图 9 膜厚波动相对标准偏差(RSD) Fig.9 Relative standard deviation (RSD) of film thickness variation |
实验测量了气相影响下洗涤冷却管内三个周向上的液膜流速分布,实验液膜雷诺数Rel为2.04×104,所得结果如下:
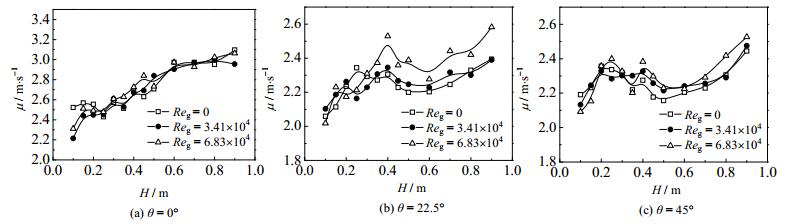
图 10为洗涤冷却环槽缝为3 mm,液膜雷诺数Rel=2.04×104时,不同气相雷诺数下液膜流速的分布图。在0°周向的液膜流速受气相影响基本没有变化,相比较22.5和45°,在洗涤冷却管下半段,气相加剧了这两个周向角处的整体速度趋势呈增加的状态且液膜波动幅度增加,此处高气相雷诺数下的液膜流速远大于单液相流动时的流速。在周向45°也可以看到高气相雷诺数使得液膜流速的最值差增大,表明气相雷诺数增大加强了气液剪切作用,αδ+增大,液膜湍流的波动程度更加剧烈,周向22.5和45°处的情况与Alekseenko S V[7]在顺流条件下的实验所得结论吻合,由于0°位置存在液膜脱离主体液膜的现象[3, 4],使得气相对液膜表面波动的影响低于其余周向。
|
图 10 不同周向下液膜速度 Fig.10 Mean velocity of liquid film at different circumferential positions |
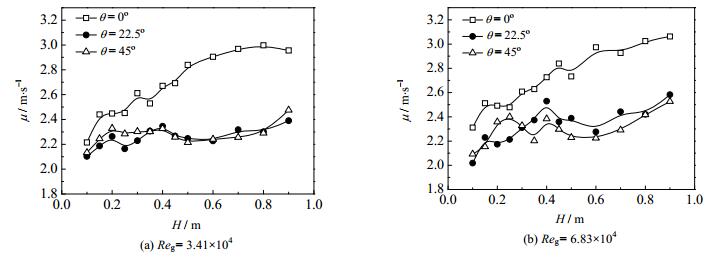
图 11比较了不同气相雷诺数下,各周向位置处液膜流速的轴向分布规律,在周向角0°处,液膜流速同厚度有相似的情况,始终在流动距离增加的过程中保持最大,由于受重力作用影响,该处液膜流速呈递增的趋势,而22.5和45°处的液膜流速则相对处在一个较低的值,并在波动中平缓上升。通过图(a)、(b)的比较,发现高气相雷诺数加剧了22.5及45°在轴向距离H=0.2~0.4 m处的波动,这也是前文提出的液膜厚度变化最明显的位置。总体而言,在本实验条件下液膜流速整体趋势受气相影响不显著。
|
图 11 不同气相雷诺数下周向液膜流速轴向分布 Fig.11 Comparison of circumferential liquid film velocities at different Reg |
(1) 通过实验发现液膜在洗涤冷却管流动过程中,存在着中央液膜向两边铺展的现象,且液膜厚度变化受气相及槽缝尺度影响在周向角8和16°上的局部位置发生了延后现象。这些变化的具体过程期望通过可视化手段来进行进一步研究。
(2) 气相雷诺数增强了气液两相间的剪切作用,整体上加剧了液膜波动幅度,并使液膜速度波动趋势更加显著,但与洗涤冷却环槽缝尺度影响贡献相比,其对液膜的影响相对较小。
(3) 洗涤冷却环槽缝尺度的增加,洗涤冷却环出口水流速由1.74降至1.06 m·s-1,使中央液膜向两边扩散的进程延后,这导致在初始段除0°外其余周向角液膜厚度分布不均严重。
符号说明:
|
|
| [1] | YU Zun-hong(于遵宏), WANG Fu-chen(王辅臣). Coal gasification technology(煤炭气化技术)[M].Beijing(北京): Chemical Industry Press(化学工业出版社), 2010. |
| [2] | WANG Ling-ping(王灵萍), WANG Yi-fei(王亦飞), GUO Qiang-qiang(郭强强), et al. Flow characteristics of vertical falling film in scrubbing cooling tube(洗涤冷却管内垂直降膜流动特性)[J]. Journal of Chemical Industry and Engineering(化工学报) , 2013, 64(6): 1959-1968. |
| [3] | WANG Jing(王晶), WANG Yi-fei(王亦飞), YAN Liu-cheng(颜留成), et al. Characteristics of velocity and thickness distribution of liquid film in vertical falling tube(管内垂直下降液膜速度与厚度分布特性)[J]. Journal of Chemical Industry and Engineering(化工学报) , 2016, 67(6): 2239-2245. |
| [4] | Yan L C, Wang Y F, Wu Z W, et al. Research of vertical falling film behavior in scrubbing-cooling tube[J]. Chemical Engineering Research and Design , 2017, 117: 627-636. DOI:10.1016/j.cherd.2016.11.010. |
| [5] | Yu Y Q, Wei S J, Yang Y H, et al. Experimental study of water film falling and spreading on a large vertical plate[J]. Progress in Nuclear Energy , 2012, 54(1): 22-28. DOI:10.1016/j.pnucene.2011.09.007. |
| [6] | Tiong J, Serifi K, Argyriadi K, et al. Solitary waves on inclined films: their characteristics and the effects on wall shear stress[J]. Experiments in Fluids , 2006, 41(1): 79-89. DOI:10.1007/s00348-006-0158-1. |
| [7] | Alekseenko S V, Markovich D M, Kharlamov S M, et al. Experimental study of the linear stability of a falling liquid film in the presence of a turbulent gas stream[J]. Fluid Dynamics , 2004, 39(4): 612-620. DOI:10.1023/B:FLUI.0000045677.40730.18. |
| [8] | Nowak M. Wall shear stress measurement in a turbulent pipe flow using ultrasound Doppler velocimetry[J]. Experiments in Fluids , 2002, 33(2): 249-255. DOI:10.1007/s00348-002-0407-x. |
| [9] | Zhou D W, Gambaryan-Roisman T, Stephan P. Measurement of water falling film thickness to flat plate using confocal chromatic sensoring technique[J]. Experimental Thermal and Fluid Science , 2009, 33(2): 273-283. DOI:10.1016/j.expthermflusci.2008.09.003. |
| [10] | Dupont J, Mignot G, Prasser H M. Two-dimensional mapping of falling water film thickness with near-infrared attenuation[J]. Experiments in Fluids , 2015, 56(5): 90-106. DOI:10.1007/s00348-015-1955-1. |
| [11] | Moran K, Inumaru J, Kawaji M. Instantaneous hydrodynamics of a laminar wavy liquid film[J]. International Journal of Multiphase Flow , 2002, 28(5): 731. DOI:10.1016/S0301-9322(02)00006-X. |
| [12] | YU Li-ming(余黎明), ZENG Ai-wu(曾爱武), YU Guo-cong(余国琮). Study on liquid velocity fluctuation and mass transfer in gas-liquid falling film flow(气液降膜流动中液相速度波动及其传质研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2006, 20(5): 696-701. |
| [13] | Gurau B, Vassallo P, Keller K. Measurement of gas and liquid velocities in an air-water two-phase flow using cross-correlation of signals from a double sensor hot-film probe[J]. Experimental Thermal and Fluid Science , 2004, 28(6): 495-504. DOI:10.1016/j.expthermflusci.2003.07.001. |
| [14] | Drosos E I P, Paras S V, Karabelas A J. Characteristics of developing free falling films at intermediate Reynolds and high Kapitza numbers[J]. International Journal of Multiphase Flow , 2004, 30(7): 853-876. |
| [15] | Kostoglou M, Samaras K, Karapantsios T D. Large wave characteristics and their downstream evolution at high Reynolds number falling films[J]. AIChE Journal , 2010, 56(1): 11-23. |
| [16] | Kostoglou M, Samaras K, Karapantsios T D. Reconstruction of film thickness time traces for wavy turbulent free falling films[J]. International Journal of Multiphase Flow , 2010, 36(3): 184-192. DOI:10.1016/j.ijmultiphaseflow.2009.11.005. |
| [17] | Karimi G, Kawaji M. Flow characteristics and circulatory motion in wavy falling films with and without counter-current gas flow[J]. International Journal of Multiphase Flow , 1999, 25(6): 1305-1319. |
| [18] | Cramer A, Zhang C, Eckert S. Local flow structures in liquid metals measured by ultrasonic doppler velocimetry[J]. Flow Measurement and Instrumentation , 2004, 15(3): 145-153. DOI:10.1016/j.flowmeasinst.2003.12.006. |
| [19] | Longo S. The effects of air bubbles on ultrasound velocity measurements[J]. Experiments in Fluids , 2006, 41(4): 593-602. DOI:10.1007/s00348-006-0183-0. |
| [20] | Chang H C. Wave evolution on a falling film[J]. Annual Review of Fluid Mechanics , 1994, 26: 103-36. DOI:10.1146/annurev.fl.26.010194.000535. |
| [21] | Henstock W H, Hanratty T J. The interfacial drag and height of the wall layer in annular flows[J]. American Institute of Chemical Engineers , 1976, 22: 990-1000. DOI:10.1002/(ISSN)1547-5905. |




