当微通道的特征尺寸与气体分子平均自由程相当或更小、且存在沿壁面切线方向的温度梯度时,气体分子会以热蠕流形式自发地由低温端流向高温端,随着流动的发展,高温端与低温端形成压差后又引起由高温端流向低温端的压力驱动流(泊肃叶流),这一现象被称为热流逸效应,由Reynolds[1]首次发现并提出。后来Knudsen[2]在此基础上设计了基于热流逸效应工作的努森压缩机(泵)的雏形,但碍于当时条件限制未得到深入研究。如今随着微/纳米技术的迅猛发展,基于热流逸效应工作的各种流体输送及升压器件,因具有无运动部件、可以低品位热能驱动等优势,再次进入人们的视野。
基于热流逸效应的升压作用,一些学者提出了针对努森泵的多种优化设计。Gutpa等[3]设计了48级串联的努森泵,其压缩比可达50左右;随后An等[4]设计了162级串联的努森泵,其压缩比能维持在844。杨林等[5]以努森压缩机替代常规压缩机,提出了一种颇具发展前景的新型努森压缩制冷方式。热流逸效应的另一重要应用则是气体输送。Pharas等[6]设计制造的双向努森泵可获得0.74 cm3·min-1的流量。An等[7]以光刻技术设计制造的努森泵在短时间内即可获得超过200 sccm的流量[8]。此外,Sugimoto等[9, 10]和Nakaye等[11]对基于热流逸效应的气体分离方法做了理论分析,后者还通过实验获得了约5%的提纯率;Bell[12]基于努森泵设计的体外药物输送系统的流量可达2.6 μL·s-1;Martini-Laithier等[13]利用热流逸效应设计了一种新型氨监测系统;Qin等[14]借助努森泵设计的气相色谱仪的理论监测范围可低至20 ppb。但上述研究均局限于某一特定场合,作为研究对象的气体涉及种类较少;且多数都着眼于过渡流领域,未综合考虑自由分子流领域的情形;最关键的是未详细探讨应用热流逸效应时所涉及的结构尺寸特征、气体特性及流态等诸要素之间的相互制约关系。从而尚不能很好地从全局上把握基于热流逸效应工作的器件的设计方法及运行特性。
热流逸效应是热驱动微型器件及装置的理论基础,由于热流逸效应涉及微尺度流动,过去针对宏观流动的研究结果基本不再适用。为此,本文以13种常见气体为研究对象,定义几何系数和净流量减少率,采用变径硬球模型(variable hard sphere, VHS)分析计算微通道内过渡流领域和自由分子流领域的热流逸效应,从而得到热流逸效应下的气体流量与压差的变化规律,为热流逸效应的实验研究和实际应用提供理论指导。
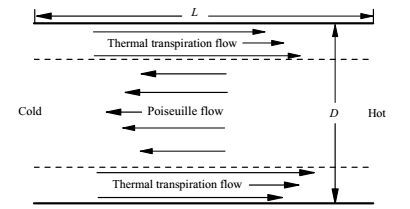
2 热流逸效应的数学描写 2.1 微通道中的热流逸模型参考图 1,假设气体在直径为D,长为L的微通道内流动,通道两端维持不同的温度,两端初始压力相同,左端为冷端,右端为热端。通常根据努森数Kn (气体分子平均自由程与微通道特征尺寸之比)或稀薄参数δ来判断气体所处的流动领域。当Kn <0.01时,流动处于连续流领域(此时不发生热流逸效应);当0.01≤ Kn <0.1时,流动处于滑移流领域(此时热流逸效应特别微弱);当0.1 ≤ Kn <10时,流动处于过渡流领域;当Kn ≥ 10时,流动处于自由分子流领域[15, 16]。努森数Kn与稀薄参数δ有如下关系:
|
图 1 微通道内的热流逸效应 Fig.1 Thermal transpiration effects in a microchannel |
| $Kn = \frac{\lambda }{D} = \frac{{\sqrt \pi }}{\delta }$ | (1) |
式中,λ为平均分子自由程,m;D为微通道直径,m;δ为稀薄参数,它与努森数Kn成反比。
发生热流逸效应时,微通道中部会出现由热端流向冷端的泊肃叶流,此时微通道内的流动为靠近微通道壁面的热流逸流与泊肃叶流的叠加,故引入热流逸流系数GT和泊肃叶流系数GP,并令
| $\gamma = \frac{{{G_{\rm{T}}}}}{{{G_{\rm{P}}}}}$ | (2) |
那么微通道两端的压力与温度有如下关系
| $\frac{{{P_{\rm{H}}}}}{{{P_{\rm{C}}}}} = {\left( {\frac{{{T_{\rm{H}}}}}{{{T_{\rm{C}}}}}} \right)^\gamma }$ | (3) |
式中,PH为热端压力,Pa;PC为冷端压力,Pa;TH为热端温度,K;TC为冷端温度,K。
定义压力系数ΨP与温度系数ΨT分别为
| ${\mathit{\Psi }_{\rm{P}}} = \frac{{\Delta P}}{{{P_{\rm{m}}}}} = \frac{{{P_{\rm{H}}} - {P_{\rm{C}}}}}{{{P_{\rm{m}}}}}$ | (4) |
| ${\mathit{\Psi }_{\rm{T}}} = \frac{{\Delta T}}{{{T_{\rm{m}}}}} = \frac{{{T_{\rm{H}}} - {T_{\rm{C}}}}}{{{T_{\rm{m}}}}}$ | (5) |
式中,ΔP为微通道两侧压差,Pa;Pm为平均压力,Pa;ΔT为微通道两端温差,K;Tm为平均温度,K。
系统运行的平均压力Pm与平均温度Tm分别为
| ${P_{\rm{m}}} = \frac{1}{2}\left( {{P_{\rm{H}}} + {P_{\rm{C}}}} \right),{T_{\rm{m}}} = \frac{1}{2}\left( {{T_{\rm{H}}} + {T_{\rm{C}}}} \right)$ | (6) |
由于气体分子平均自由程是建立在分子碰撞的基础之上的,因此需要选定分子碰撞模型来确定气体分子的平均自由程,为此采用更接近实际气体分子碰撞的变径硬球模型(VHS)来确定分子平均自由程λ,其表达式如下[15]
| $\lambda {\rm{ = }}\frac{{4\alpha \left( {7{\rm{ - }}2\omega } \right)\left( {{\rm{5 - }}2\omega } \right)}}{{5\left( {\alpha {\rm{ + }}1} \right)\left( {\alpha {\rm{ + 2}}} \right)}}{\left( {\frac{m}{{2\pi kT}}} \right)^{{\rm{1/2}}}}\frac{\mu }{\rho }$ | (7) |
式中,α为协调系数,对于VHS分子模型,α = 1[15];ρ为气体密度,kg·m-3;ω为黏性系数指数[17];T为温度,K;k为玻尔兹曼常数,k = 1.38066×10-23 J·K-1;μ为黏性系数,N·s·m-2,可由参考状态下的黏性系数μref求得,即[17]
| $\mu {\rm{ = }}{\mu _{{\rm{ref}}}}{\left( {\frac{T}{{{T_{{\rm{ref}}}}}}} \right)^\omega }$ | (8) |
随着气体沿微通道长度方向的流动距离不断增大,气体分子与壁面碰撞发生漫反射后反向运动的几率也越大,为描述微通道长度的影响,定义几何系数LND (微通道长度与直径之比)
| ${L_{{\rm{ND}}}} = \frac{L}{D}$ | (9) |
式中,L为微通道的长度,m。
在文献[18]的研究基础上,引入几何系数整理并化简可得则通过微通道的净质量流量为
| $M = \left( {\frac{m}{{{\rm{2}}k{T_{\rm{m}}}}}} \right)A{P_{\rm{m}}}\frac{1}{{{L_{{\rm{ND}}}}}}\left( {{\mathit{\Psi }_{\rm{T}}}{G_{\rm{T}}} - {\mathit{\Psi }_{\rm{P}}}{G_{\rm{P}}}} \right)$ | (10) |
式中,A为微通道横截面积,m2。由式(1)可知,微通道的特征尺寸D与努森数Kn相互约束,可见一旦努森数Kn确定,微通道的几何结构便基本确定,即
| ${L_{{\rm{ND}}}} = \frac{{LKn}}{\lambda },A = \frac{\pi }{4}{\left( {\frac{\lambda }{{Kn}}} \right)^2}$ | (11) |
最后,令净质量流量减少率为
| ${\mathit{\Psi }_{\rm{M}}}{\rm{ = }}\frac{M}{{{M_{{\rm{max}}}}}}$ | (12) |
式中,Mmax为气体的最大净质量流量,kg·s-1。
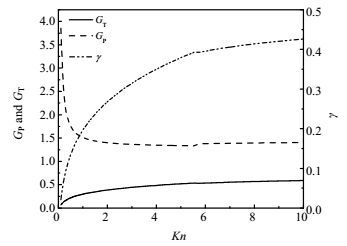
2.2 微通道中的过渡流当努森数Kn∈[0.1, 10)时,微通道内的气体处于过渡流领域[15, 16]。根据Sone[18]等的实验数据可拟合出热流逸流系数GT、泊肃叶流系数GP以及γ与努森数Kn的关系,见图 2。式(10)中虽然并未明显包含努森数Kn,但其中的面积A、几何系数LND、热流逸流系数GT及泊肃叶流系数GP均与努森数Kn相关。
|
图 2 过渡流中热流逸流系数GT、泊肃叶流系数GP和γ随努森数Kn的变化 Fig.2 Profiles of thermal transpiration coefficient GT, Poiseuille coefficient GP and γ as a function of Knudsen number Kn in transitional flow regime |
当努森数Kn ≥10时,微通道内的气体处于自由分子流领域[15, 16]。在该流域中,当努森数趋于无穷大时,气体分子的平均自由程远大于微通道的特征尺寸,此时分子间发生碰撞的概率非常小,因此在高度稀薄的自由分子流领域,仅存在分子与壁面间的完全弹性碰撞。而对于在努森数为有限大小的自由分子流初始阶段,分子间的碰撞不可忽略,为定量计算,仍需要基于分子碰撞模型确定气体分子平均自由程,研究表明VHS模型依旧适用[17]。根据Knudsen[2]的研究,在自由分子流领域,微通道两侧的压差达到最大,此时γ = 0.5;此外在该流动领域中泊肃叶流系数GP与热流逸流系数GT都是定值,分别为[19]
| ${G_{\rm{T}}} = \frac{1}{2}{G_{\rm{P}}},{G_{\rm{P}}} = \frac{8}{{3\sqrt \pi }}$ | (13) |
进而根据式(10)便可确定自由分子流初始阶段的净质量流量M,该流域下的净质量流量仍旧与努森数Kn相关。
3 热流逸效应作用下的压力与流量变化 3.1 微通道尺寸特征及气体流态的影响从式(1)和(11)可看出在发生热流逸效应的前提下,微通道尺寸与气体流态是相互关联耦合的,故应将它们放在一起讨论。选取13种常见气体为研究对象,它们在参考温度下的部分参数见表 1。
| 表 1 参考温度Tref = 273 K下的气体参数[18] Table 1 Properties of gases at reference temperature Tref = 273 K |
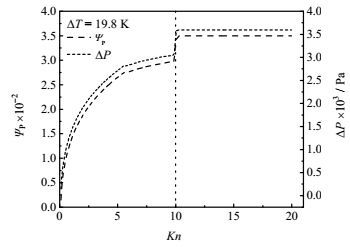
随着微通道内气体不断由冷端流向热端,微通道两端会逐渐形成压差,13种气体在微通道两端形成的压差ΔP和压力系数ΨP随努森数Kn的变化见图 3。在过渡流领域(0.1≤ Kn <10),通道两端压差ΔP和压力系数ΨP随努森数Kn的增大而增大,越接近自由分子流领域压差越大;进入自由分子流领域后压差为一常数,与努森数Kn无关,因为在该流域热流逸流系数GT和泊肃叶流系数GP均为定值。压差ΔP在Kn = 10处出现跃迁,这是由于自由分子流领域与过渡流领域有不同的机制,导致两个领域内的计算公式不同。综合来看,过渡流领域微通道两端的压差ΔP随努森数Kn的增大而增大,进入自由分子流领域达最大值,比过渡流领域的峰值大17.8%左右。可见,若将热流逸效应应用于升压为主的场合,控制微通道内气体处于自由分子流领域更为有利。
|
图 3 努森数Kn对压力差ΔP与压力系数ΨP的影响 Fig.3 Effects of Knudsen number Kn on pressure difference ΔP and pressure coefficient ΨP |
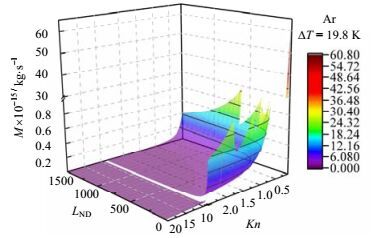
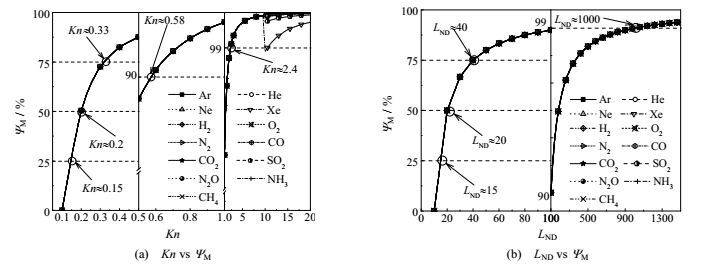
当冷热端温差为ΔT= 19.8 K (TC= 273.2 K,TH= 293 K)时,以氩气为例,探讨净质量流量M与努森数Kn和几何系数LND的关系,见图 4。气体在微通道内的净质量流量M随着努森数Kn与几何系数LND的增大而减小,其原因是为保证在微通道内流动的气体发生热流逸效应,努森数Kn增大将导致微通道直径减小,进而微通道的横截面积减小,最终流量不断减小。进一步计算表明,另外12种气体也存在与氩气类似的规律。因此对于结构一定的单个微通道,其能通过的净流量存在极限值,需要通过并联多个微通道以满足较大流量的应用场合。相比于长度,微通道的直径(特征尺寸)对流量的影响更大,所以若要获得较大的净流量,应先根据热流逸产生的条件确定微通道直径(特征尺寸),然后根据几何系数计算微通道长度。计算还发现,对于所研究的13种气体,相较于在Kn = 0.1、ΔT = 19.8 K、LND= 10的条件下的净质量流量,当努森数Kn分别达到0.15、0.2、0.33和0.58左右时,所有气体的净质量流量都相应减少了25%、50%、75%和90%,见图 5(a);而当几何系数LND分别达到15、20、40和100左右时,所有气体的净质量流量也均相应减少了25%、50%、75%和90%,见图 5(b);而当努森数Kn达到2.4左右或几何系数LND达到1000左右时,微通道内的净质量流量衰减99%。可见,应根据具体应用场合允许的净流量减少率调控微通道内的流动处于一定的努森数范围,且选择或制造微通道时应注意其长度与直径(特征尺寸)的约束关系。这是因为微通道长度越长,气体分子与壁面碰撞次数越多,导致气体分子在碰撞壁面发生漫反射后反向运动的机率增大,使净流量有所衰减。以上分析表明为了有效利用热流逸效应的输送性能,应当视具体应用需求来确定合适的流态与微通道结构。
|
图 4 努森数Kn与几何系数LND对氩气净质量流量M的影响 Fig.4 Effects of Knudsen number Kn and geometric coefficient LND on net mass flow M for Ar |
|
图 5 努森数Kn与几何系数LND对净质量流量减少率ΨM的影响 Fig.5 Effects of Knudsen number Kn and geometric coefficient LND on reduction ratio of net mass flow ΨM |
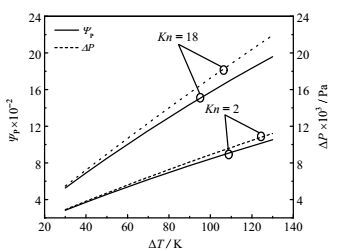
由前述理论分析可知,温差对压差的影响与气体种类无关。参考图 6,当两端温差由30 K上升至130 K (TC= 270 K,TH= 300~400 K)时,微通道两端压差近似线性地增加;温差每升高10 K,两端压差在过渡流领域平均增大约14.7%、在自由分子流领域平均增大约15.1%。压力系数随温差的变化规律与压差的类似。
|
图 6 温差ΔT对压差ΔP与压力系数ΨP的影响 Fig.6 Effects of temperature difference ΔT on pressure difference ΔP and pressure coefficient ΨP |
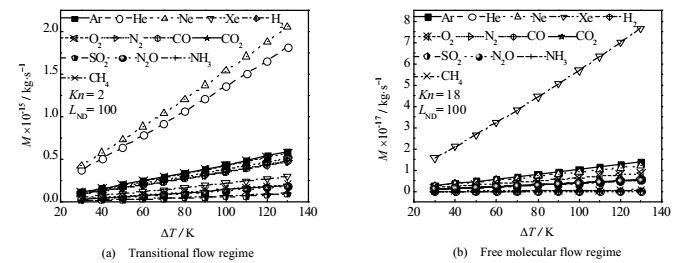
微通道两端的温差决定了其内部热流逸流的强弱。参考图 7,可发现在相同温差下,不同种类气体的质量流量不同,但它们的净质量流量均随温差的增大而近似线性地增大;当两端温差由30 K上升至130 K (TC= 270 K,TH= 300~400 K)时,温差每升高10 K,过渡流领域和自由分子流领域的净质量流量平均分别增大17.1%~19%和16.7%~18.4%,氦气的平均增长率最小,而氨气的平均增长率最大。其原因在于,微通道两端温差增大使得引发热流逸效应的动力增强,从而使流量与压差均增大;加之温差升高又导致平均温度增大,引起气体分子平均自由程增大,在微通道直径(特征尺寸)不变的前提下也会导致热流逸效应增强。此外,在过渡流领域黏性指数较大的气体(NH3、SO2、N2O等)其净质量流量的增长率较大。
|
图 7 温差ΔT对净质量流量M的影响 Fig.7 Effects of temperature difference ΔT on net mass flow M |
总之,增大温差对于增加流量和提升压力均是有利的,但在实际应用中长时间维持大温差的难度较高,故需要权衡提升温差的经济性与可行性,实现最大限度地保持微通道两端较大的温差以满足压差和流量的需求。
3.3 问题讨论就压差特性而言,其与气体的固有性质无明显关系,但与气体流态有密切关系。在过渡流领域,努森数越大则微通道两端压差越高,在自由分子流领域,压差与努森数无关且能达到特定条件下(指微通道结构、微通道两端温差等确定时)的最大值;因此对以升压为主的应用,如设计努森压缩机时,应适当减小微通道直径(特征尺寸)以使其内产生靠近自由分子流领域的热流逸效应。另一方面,从过渡流到自由分子流,流量与压差完全相反的变化趋势意味着在对流量与压差同时有一定要求的应用,如真空泵,就需要权衡二者间的关系,使设备的综合性能最优,不可仅仅只追求流量或压差单方面的性能。
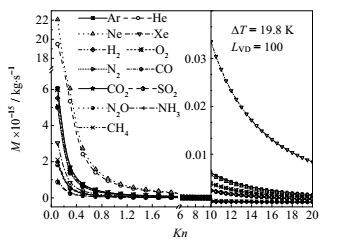
就质量流量特性而言,参考图 8,发现在过渡流领域,Ne的净质量流量始终最大,SO2的始终最小,且在该领域内大部分非极性分子气体(CO2,CH4,N2,O2,H2, ,Ar,Ne,Xe等)的净质量流量高于极性分子气体(SO2,NH3,N2O等);黏性指数较小的气体(Ne、He、H2等)其净质量流量较大。而在自由分子流领域,如图 5(a)与图 8所示,分子质量较大的气体(Xe、SO2、N2O、CO2等)其净质量流量较大,再者黏性较大的气体(Ne、Ar、Xe等)其净质量流量也较大,使得部分气体的净质量流量在该流动领域初始阶段较过渡流末段有小幅度增加。因此对于纯粹输送气体的应用,即要求流量尽可能大的场合,利用热流逸效应处理Ar,He,Ne,Xe,H2,O2,N2等非极性分子气体效果较好;而利用热流逸效应来分离气体,即要求混合气体不同组分有显著流量差异的场合,那么处理极性分子与非极性分子气体组成的混合气体,或黏性指数相差较大的气体组成的混合气体,可获得较高分离效率。此外,微通道的几何系数对流量也有显著影响,由于必须保证热流逸发生的条件(努森数在一定范围内),因此一旦给定应用要求(压差或流量),微通道的直径(特征尺寸)和长度也就基本确定;而对于结构确定的微通道,其所能获得的最大净质量流量是确定的。
|
图 8 努森数Kn对气体净质量流量的影响 Fig.8 Effects of Knudsen number Kn on net mass flow of gases |
(1) 热流逸效应的流量和升压特性与微通道的结构尺寸特征、气体特性及流态等因素密切相关。净质量流量随努森数与几何系数的增大而减小,在过渡流初始阶段即迅速衰减,当努森数达2.4左右或几何系数达1000左右时净质量流量均减少99%。在过渡流领域,多数非极性分子气体的净质量流量高于极性分子气体;黏性指数较小的气体其净质量流量较大。而在自由分子流领域,分子质量较大或黏性较大的气体其净质量流量较大。压差在过渡流领域随努森数增大而增大,在自由分子流领域达到最大值并恒定,且较过渡流领域的峰值高约17.8%。一旦给定应用要求(压差或流量),微通道的直径(特征尺寸)和长度便基本确定;而对于结构确定的微通道,其所能获得的最大净流量是确定的。
(2) 温差是热流逸效应的驱动力。相同条件下,过渡流领域与自由分子流领域的净质量流量和压差均随微通道两端温差的升高而近似线性地增大,温差每升高10 K,净质量流量与压差分别平均增大约18%和15%。黏性指数较大的气体其净质量流量在过渡流领域受温差的影响较大,而压差在自由分子流领域随温差变化的增长率略微高于在过渡流领域的。
(3) 侧重热流逸效应升压特性的应用将流态控制在自由分子流领域效果较好。侧重热流逸效应流量特性的应用,须注意几何系数的影响并尽可能将流态控制在过渡流初始段。纯粹输送气体的场合,处理非极性分子气体较为有利;而对于气体分离,处理极性分子气体与非极性分子气体组成的混合气体或气体组分黏性指数相差较大的混合气体较为有利。对流量与压力均有一定需求的场合,则需要权衡二者的关系。此外,在设计基于热流逸效应工作的装置时还应当充分考虑提升温差的可行性与经济性。
符号说明:
| A | -微通道横截面积,m2 | ΔP | -微通道两侧压差,Pa |
| D | -微通道直径,m | ΔT | -微通道两侧温差,K |
| GP | -泊肃叶流系数 | λ | -分子平均自由程,m |
| GT | -热流逸流系数 | μ | -黏性系数,N·m·s-2 |
| Kn | -努森数 | ρ | -气体密度,kg·m-3 |
| k | -玻尔兹曼常数,J·K-1 | ω | -黏性指数 |
| L | -微通道长度,m | ΨM | -净质量流量减少率 |
| LND | -几何系数 | ΨP | -压力系数 |
| m | -分子质量,kg | ΨT | -温度系数 |
| M | -净质量流量,kg·s-1 | 下标 | |
| P | -压力,Pa | C | -微通道低温侧 |
| T | -温度,K | H | -微通道高温侧 |
| α | -协调系数 | m | -平均 |
| δ | -稀薄参数 |
| [1] | Reynolds O. On certain dimensional properties of matter in the gaseous state. Part Ⅰ & Ⅱ[J]. Philosophical Transactions of the Royal Society of London , 1879, 170: 727-845. DOI:10.1098/rstl.1879.0078. |
| [2] | Knudsen M. Eine Revision der Gleichgewichtsbedingung der Gase. Thermische Molekularströmung[J]. Annalen der Physik , 1909, 336: 205-229. DOI:10.1002/(ISSN)1521-3889. |
| [3] | Gupta N K, An S, Gianchandani Y B. A monolithic 48-stage Si-micromachined Knudsen pump for high compression ratios [C]//25th International Conference on Micro Electro Mechanical Systems (MEMS). Paris: IEEE, 2012: 152-155. |
| [4] | An S, Gupta N K, Gianchandani Y B. A Si-micromachined 162-stage two-part Knudsen pump for on-chip vacuum[J]. Journal of Microelectromechanical Systems , 2014, 23(2): 406-416. DOI:10.1109/JMEMS.2013.2281316. |
| [5] | YANG Lin(杨林), LU Wei(卢苇), CAO Cong(曹聪), et al. Design and performance analyses of refrigeration systems with Knudsen compressors(努森压缩制冷系统的设计及性能分析)[J]. Cryogenics(低温工程) , 2015(1): 37-44. |
| [6] | Pharas K, McNamara S. Knudsen pump driven by a thermoelectric material[J]. Journal of Micromechanics and Microengineering , 2010, 20(12): 125032. DOI:10.1088/0960-1317/20/12/125032. |
| [7] | An S, Qin Y, Gianchandani Y B. A monolithic Knudsen pump with 20 sccm flow rate using through-wafer ONO channels [C]//27th International Conference on Micro Electro Mechanical Systems (MEMS). San Francisco: IEEE, 2014: 112-115. |
| [8] | An S, Qin Y, Gianchandani Y B. A monolithic high-flow Knudsen pump using vertical Al2O3 channels in SOI[J]. Microelectromechanical Systems , 2015, 24(5): 1606-1615. DOI:10.1109/JMEMS.2015.2426699. |
| [9] | Sugimoto H, Shinotou A. Gas separator with the thermal transpiration in a rarefied gas[C]//27th International Symposium on Rarefied Gas Dynamics. New York:AIP Publishing, 2011, 1333(1):784-789. |
| [10] | Sugimoto H, Hibino M. Numerical analysis on gas separator with thermal transpiration in micro channels[C]//28th International Symposium on Rarefied Gas Dynamics. Zaragoza:AIP Publishing, 2012, 1501:794-801. |
| [11] | Nakaye S, Sugimoto H. Demonstration of a gas separator composed of Knudsen pumps[J]. Vacuum , 2016, 125: 154-164. DOI:10.1016/j.vacuum.2015.12.015. |
| [12] | Bell A D. Human powered Knudsen pump for pneumatic pharmaceutical delivery[D]. Kentucky:University of Louisville, 2013. |
| [13] | Martini-Laithier V, Graur I, Bernardini S, et al. Ammonia detection by a novel pyrex microsystem based on thermal creep phenomenon[J]. Sensors and Actuators B:Chemical , 2014, 192: 714-719. DOI:10.1016/j.snb.2013.10.120. |
| [14] | Qin Y, Gianchandani Y B. An all electronic, fully microfabricated micro gas chromatograph[C]//18th International Conference on Solid-State Sensors, Actuators and Microsystems, 2015 Transducers. Alaska:IEEE, 2015:626-629. |
| [15] | SHEN Qing(沈青). Rarefied gas dynamics(稀薄气体动力学)[M].Beijing(北京): National Defense Industry Press(国防工业出版社), 2003. |
| [16] | Gad-el-Hak M. The MEMS handbook[M].2nd ed. Boca Raton: CRC Press, 2006. |
| [17] | Bird G A. Molecular gas dynamics and the direct simulation of gas flows[M].New York: Oxford University Press, 1994. |
| [18] | Sone Y, Itakura E. Analysis of Poiseuille and thermal transpiration flows for arbitrary Knudsen numbers by a modified Knudsen number expansion method and their database[J]. Journal of the Vacuum Society of Japan , 1990, 33(3): 92-94. DOI:10.3131/jvsj.33.92. |
| [19] | Sharipov F, Kalempa D. Gaseous mixture flow through a long tube at arbitrary Knudsen numbers[J]. Journal of Vacuum Science & Technology A:Vacuum, Surfaces, and Films , 2002, 20(3): 814-822. |




