现代流程工业过程规模日益扩大,过程监测是保证过程生产安全、产品质量的关键。集散控制系统和计算机技术的蓬勃发展,推动了基于多元统计过程监测方法的发展[1-6]。传统多元统计方法假设过程采样之间是时序独立的,多元统计算法在特征提取时只能提取过程的稳态特征。在现代工业过程中,变量之间、操作单元之间有实际意义的耦合关系,因此过程数据会表现出时间上的动态性。动态主成分分析(principal component analysis,PCA)、动态独立成分分析等算法通过扩展矩阵方法来处理过程动态性问题[7-11]。近年来,慢特征分析(slow feature analysis, SFA)算法被引入过程监测领域[12],SFA算法根据特征的变化提取动态特征,适用于动态过程监测。Guo等[13]提出概率SFA算法;Shang等[14]明确指出动态性是表征过程变化的重要指标;Zhang等[15]将核SFA算法用于非线性间歇过程;张汉元等[16]结合核慢特征判别分析和支持向量数据描述算法,改善过程的非线性特性。上述改进的SFA故障检测算法在特征选择与观测统计量构造方面,通过离线挑选部分重要特征构造统计量,没有充分利用在线监测数据的故障信息,可能造成故障信息无法有效表达。Ge等[17]提出从全局监测性能出发的基于故障样本的独立元监测方法。Jiang等[18]提出基于在线挑选敏感主成分的敏感PCA算法。Huang等[12]提出基于慢特征分析的在线特征重排和特征提取监测策略。这些算法是基于在线特征选择策略的过程监测算法,然而此类在线策略的研究仍不完善,在处理过程动态性方面以及特征选择的鲁棒性方面仍需要改进。因此,如何采用在线特征提取策略进行动态特征选择,加强故障信息在监测模型的表达,提高监测模型的监测效果值得深入研究。为解决这一问题,本文提出基于选择在线故障相关特征的SFA故障检测算法,经过SFA特征提取,在线选择超过阈值的特征为故障相关特征,并构造监测统计量进行故障检测。
2 慢特征分析(SFA)对于在时间区间
| $\mathop {\min }\limits_{{g_i}( \cdot )} {\left\langle {\dot s_i^2} \right\rangle _t}$ | (1) |
约束为
| ${\left\langle {{s_i}} \right\rangle _t} = 0\;\;\;(\rm{zero\;mean}), $ | (2) |
| ${\left\langle {s_i^2} \right\rangle _t} = 1\;\;\;\;(\rm{unit\;\operatorname{variance}} ), $ | (3) |
| $\forall i \ne j:\;\;\;\;\;{\left\langle {{s_i}{s_j}} \right\rangle _t} = 0\;\;(\rm{decorrelation}\;{\rm{and}}\;{\rm{order}})$ | (4) |
式中:
SFA可以提取正常数据中缓慢变化的特征,慢特征的线性变换可以写作原始变量的线性组合,如式(5)所示。
| $\mathit{\boldsymbol{s}} = {\mathit{\boldsymbol{Wx}}}$ | (5) |
式中:
| $\begin{gathered} \mathop {\min }\limits_{{\mathit{\boldsymbol{w}}_i}( \cdot )} {\left\langle {\dot s_i^2} \right\rangle _t}{\rm{ = }}\mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{w}}_i}} \mathit{\boldsymbol{w}}_i^{\rm{T}}\left\langle {{\bf{\mathit{\boldsymbol{\dot x}}}}(t){\bf{\mathit{\boldsymbol{\dot x}}}}{{(t)}^{\rm{T}}}} \right\rangle \mathit{\boldsymbol{w}}_i^{} = \mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{w}}_i}} \mathit{\boldsymbol{w}}_i^{\rm{T}}{\mathit{\boldsymbol{Rw}}}_i^{} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{\left\langle {s_i^2} \right\rangle _t} = \mathit{\boldsymbol{w}}_i^{\rm{T}}\left\langle {\mathit{\boldsymbol{x}}(t)\mathit{\boldsymbol{x}}{{(t)}^{\rm{T}}}} \right\rangle \mathit{\boldsymbol{w}}_i^{} = \mathit{\boldsymbol{w}}_i^{\rm{T}}{\mathit{\boldsymbol{Cw}}}_i^{} = 1\;\; \\ \end{gathered} $ | (6) |
式中:矩阵
| $\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{w}}_i} = {\lambda _i}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{w}}_i}$ | (7) |
经过广义特征值求解权重变换矩阵,可自动满足约束(4)。将特征值
SFA可以提取过程中不同动态水平的特征,根据特征变化的缓慢程度排列。在实际动态工业过程中,故障可能发生在任何的动态特征中,因此经过SFA进行动态特征提取,下一步需要选择重要特征对数据降维。由于SFA是一种线性特征提取方法,通常认为权重矩阵W中具有较大L2范数的行对应的慢特征能够捕捉到过程的变化。对于第i个慢特征,其权重向量的L2范数li表示为
| ${l_i} = \sum\limits_{j = 1}^m {{W_{ij}}^2} $ | (8) |
式中:
| $\sum\limits_{i = 1}^k {{l_i}} /\sum\limits_{i = 1}^m {{l_i}} > 90\% $ | (9) |
基于权重矩阵L2范数的特征选择策略是一种离线特征选择策略,离线方法只能预先选定若干个特征。而实际过程中,不同的故障可能表征在不同的特征中,离线方法没有利用到实时的故障信息,选中的特征可能不全是故障相关特征,造成信息冗余,监测模型的有效性低。因此,应充分利用在线监测样本信息,选择故障相关特征对数据降维,构造监测统计量。
3.1 选择故障相关特征策略对于一个
| ${\mathit{\boldsymbol{s}}_\rm{test}} = \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{x}}_\rm{test}}$ | (10) |
由慢特征的约束条件可知,根据正常数据提取的慢特征是标准化为零均值单位方差的。对于在线监测,每个慢特征统计量可以表示为
| ${s^2}_1, {s^2}_2, \cdots , {s^2}_m(i = 1, 2, \cdots , m)$ | (11) |
因此慢特征统计量越大,可能包含更多过程变化信息。离线控制限
| ${s^2}_i > S_{\lim }^2/k$ | (12) |
为了减少过程随机噪声对特征的影响,引入滑动窗口
| ${\mathit{\boldsymbol{S}}_\rm{test}} = \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{X}}_\rm{test}}$ | (13) |
每个特征窗口内均值可以表示为
| ${\bar s_i^2}\; = \frac{{\mathit{\boldsymbol{s}}{{_{\rm{test}}^i}^{\rm{T}}}\mathit{\boldsymbol{s}}_{\rm{test}}^i}}{h}$ | (14) |
以特征均值
记
| ${S^{\rm{2}}} = \mathit{\boldsymbol{s}}_d^{\rm{T}}\mathit{\boldsymbol{s}}_d^{}$ | (15) |
在正常数据提取的慢特征中挑选出当前样本的故障相关特征,由KDE估计出当前监测样本的控制限。若所有在线慢特征统计量都没有超过平均阈值,则此选择故障相关慢特征分析(fault-related SFA,FRSFA)算法退化为SFA算法,采用离线特征选择策略进行降维。
传统方法在建立监测统计量时,通常分别构造特征空间和残差空间两个统计量,特征空间和残差空间的统计量互为补充。本文提出在线选择故障相关特征的降维策略,经过特征选择,故障信息被集中在慢特征空间,残差空间几乎不包含故障信息,本文只建立慢特征空间的
基于选择故障相关特征的SFA故障检测算法的详细步骤如下。
离线建模:
第1步:收集正常工况下的数据,并对数据进行0均值和单位方差标准化;
第2步:采用SFA算法提取过程数据的动态特征,并获取权重矩阵
第3步:根据权重向量的L2范数选择部分重要的慢特征;
第4步:根据选择的慢特征构造监测统计量,并采用KDE算法估计统计量的阈值。
在线监测:
第1步:确定滑动窗口宽度
第2步:根据离线建模第2步的权重矩阵,计算监测样本的慢特征统计量
第3步:对比每个慢特征统计量和离线建模第4步得到的平均阈值,挑选出超过平均阈值的慢特征为故障相关特征;
第4步:建立故障相关特征统计量;
第5步:返回离线建模第4步,根据当前挑选的慢特征建立正常数据的统计量,并估计过程的控制限;
第6步:对比监测统计量和控制限,判断当前监测样本是否为故障。
4 Tennessee Eastman (TE)过程仿真实验TE过程对于研究过程监测方法提供了很大帮助,已经被学术界广泛认可[22-23]。TE过程有4个反应,共生成2种有效产物。这个过程有5个主要的单元操作:反应器、冷凝器、分离器、循环压缩机和气提塔。本文中的研究选取22个连续测量变量和11个操纵变量用于故障检测,TE过程仿真模型预设定21个故障。过程正常数据包含500个样本。对于每个故障,故障数据包含960个样本,其中前160个样本是正常数据,161至960个样本为故障数据。
本文对比PCA、SFA、FRSFA 3种算法的监测效果,选取滑动窗口
|
|
表 1 PCA、SFA、FRSFA故障检测率 Table 1 Fault detection rates of PCA, SFA and FRSFA |
对于故障1、2、4、6、7、8及14这类故障幅值较大的故障,3种方法几乎都能达到100%故障检测率。对于故障5、12、13、17、18及19,FRSFA的故障检测率能够与其它2种算法中最好的监测效果持平。提出的FRSFA算法在检测故障10、11、15、16、20及21时比其它2种算法有明显优势。故障3、9及15是公认的几乎无法检测的故障,3种算法都不能检测出故障3和9,本文提出的FRSFA算法对故障15的检测率达到了0.34,显著高于其他2种算法。本文提出的FRSFA算法充分提取过程的动态特征,根据在线样本选择故障相关信息,排除故障无关特征对监测结果的影响,相比于PCA和SFA算法,监测模型的有效性提高。为了进一步说明提出算法在选择故障相关特征方面的优势,以故障11为例,图 1、2分别给出了根据L2范数排序的、根据在线特征大小排序的所有特征图。
|
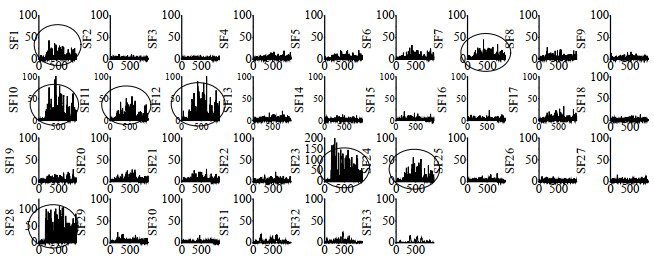
图 1 根据权重向量L2范数排序的所有慢特征 Fig.1 All SFs in the order of L2 norm of the weight vector |
|
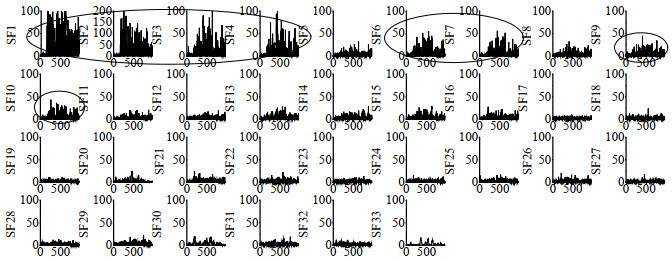
图 2 根据在线特征大小排序的所有慢特征 Fig.2 All SFs in the order of their values |
图 1是将特征按照权重向量的L2范数排序的所有慢特征图,具有显著故障信息的特征(特征10、12、23、28)和较多故障信息的特征(特征1、7、11、24)在图中用圈标出,由于TE过程离线特征个数k=21,仍然有3个表征故障信息的特征没有被挑选,导致特征空间的重要信息不足。因此,此特征选择方式有局限性,会导致监测效果不佳。图 2是根据在线特征的大小进行排序的慢特征图。可以看出,无论是显著表征故障的特征(特征1、2、3、4)还是较为显著表征故障的特征(特征6、7、9、10)都排在前位,进行特征选择时,这些特征超过了平均阈值,被挑选到特征空间,充分利用了过程的故障信息,提高了模型的有效性。
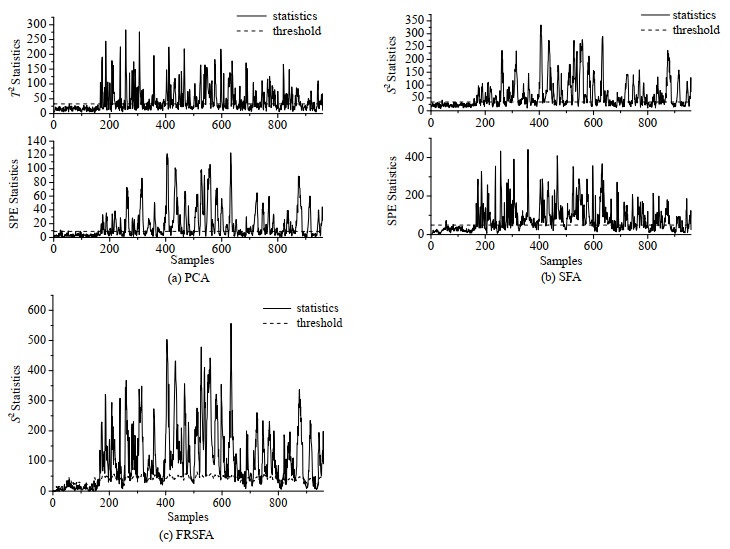
故障11是反应器冷却水进口温度的随机变化,图 3(a)~(c)分别给出了PCA、SFA和FRSFA的监测效果。PCA算法的
|
图 3 故障11监测图 Fig.3 Monitoring results of fault 11 |
SFA算法在进行降维时采用离线特征选择策略,没有充分利用在线样本的故障信息,导致特征空间信息冗余,监测模型的有效性降低。本文提出基于在线故障相关特征选择SFA过程监测策略,首先计算出每个慢特征的阈值,将其作为挑选的基准;然后通过对比在线特征与阈值的大小,确定超过平均阈值的特征作为故障相关特征;最后采用核密度估计实时估计当前样本的控制限。采用SFA算法提取过程的本质动态特征,克服了传统静态算法在动态过程监测方面的不足,提出的在线故障特征选择策略排除了故障无关特征对监测效果的影响,提高了监测模型的有效性。在TE过程进行仿真实验,相比于PCA和SFA算法,提出的FRSFA算法监测性能更优。
SFA算法能够提取出过程的动态特征,取得优异的监测效果。然而,本文研究的SFA算法是一种线性特征提取算法,没有考虑到复杂工程的非线性特点,基于SFA算法的改进算法还有很大的发展空间。同时,工业过程规模大、变量关系复杂,如何挖掘更多的工业过程信息,仍然值得研究。
| [1] |
潘怡君, 杨春节, 孙优贤, 等. 基于主成分追踪方法的过程监测[J]. 中南大学学报(自然科学版), 2017, 48(1): 127-133. PAN Y J, YANG C J, SUN Y X, et al. Process monitoring based on principal component pursuit[J]. Journal of Central South University (Science and Technology), 2017, 48(1): 127-133. |
| [2] |
郭金玉, 王鑫, 李元. 基于加权差分主元分析的化工过程故障检测[J]. 高校化学工程学报, 2018, 32(1): 183-192. GUO J Y, WANG X, LI Y. Fault detection in chemical processes using weighted differential principal component analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(1): 183-192. |
| [3] |
周东华, 胡艳艳. 动态系统的故障诊断技术[J]. 自动化学报, 2009, 35(6): 748-758. ZHOU D H, HU Y Y. Fault diagnosis techniques for dynamic systems[J]. Acta Automatica Sinica, 2009, 35(6): 748-758. |
| [4] |
QIN S J. Statistical process monitoring:Basics and beyond[J]. Journal of Chemometrics, 2003, 17(8/9): 480-502. |
| [5] |
GE Z Q, SONG Z H, GAO F R. Review of recent research on data-based process monitoring[J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562. |
| [6] |
GE Z Q, CHEN J H. Plant-wide industrial process monitoring:A distributed modeling framework[J]. IEEE Transactions on Industrial Informatics, 2016, 12(1): 310-321. DOI:10.1109/TII.2015.2509247 |
| [7] |
KU W, STORER R H, GEORGAKIS C. Disturbance detection and isolation by dynamic principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1995, 30(1): 179-196. DOI:10.1016/0169-7439(95)00076-3 |
| [8] |
LI R Y, RONG G. Fault isolation by partial dynamic principal component analysis in dynamic process[J]. Chinese Journal of Chemical Engineering, 2006, 14(4): 486-493. DOI:10.1016/S1004-9541(06)60103-1 |
| [9] |
RUSSELL E L, CHIANG L H, BRAATZ R D. Fault detection in industrial processes using canonical variate analysis and dynamic principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 2000, 51(1): 81-93. DOI:10.1016/S0169-7439(00)00058-7 |
| [10] |
CHEN J H, LIU K C. On-line batch process monitoring using dynamic PCA and dynamic PLS models[J]. Chemical Engineering Science, 2002, 57(1): 63-75. DOI:10.1016/S0009-2509(01)00366-9 |
| [11] |
LEE J M, YOO C, LEE I B. Statistical monitoring of dynamic processes based on dynamic independent component analysis[J]. Chemical Engineering Science, 2004, 59(14): 2995-3006. DOI:10.1016/j.ces.2004.04.031 |
| [12] |
HUANG J, ERSOY O K, YAN X F. Slow feature analysis based on online feature reordering and feature selection for dynamic chemical process monitoring[J]. Chemometrics and Intelligent Laboratory Systems, 2017, 169: 1-11. DOI:10.1016/j.chemolab.2017.07.013 |
| [13] |
GUO F H, SHANG C, HUANG B, et al. Monitoring of operating point and process dynamics via probabilistic slow feature analysis[J]. Chemometrics and Intelligent Laboratory Systems, 2016, 151: 115-125. DOI:10.1016/j.chemolab.2015.12.017 |
| [14] |
SHANG C, HUANG B, YANG F., et al. Slow feature analysis for monitoring and diagnosis of control performance[J]. Journal of Process Control, 2016, 39: 21-34. DOI:10.1016/j.jprocont.2015.12.004 |
| [15] |
ZHANG H Y, TIAN X M, DENG X G. Batch process monitoring based on multiway global preserving kernel slow feature analysis[J]. IEEE Access, 2017, 5: 2696-2710. |
| [16] |
张汉元, 田学民. 基于KSFDA-SVDD的非线性过程故障检测方法[J]. 化工学报, 2016, 67(3): 827-832. ZHANG H Y, TIAN X M. Nonlinear process fault detection based on KSFDA and SVDD[J]. CIESC Journal, 2016, 67(3): 827-832. |
| [17] |
GE Z Q, SONG Z H. Performance-driven ensemble learning ICA model for improved non-Gaussian process monitoring[J]. Chemometrics and Intelligent Laboratory Systems, 2013, 123: 1-8. DOI:10.1016/j.chemolab.2013.02.001 |
| [18] |
JIANG Q C, YAN X F, ZHAO W X. Fault Detection and diagnosis in chemical processes using sensitive principal component analysis[J]. Industrial & Engineering Chemistry Research, 2013, 52(4): 1635-1644. |
| [19] |
WISKOTT L. Slow feature analysis:A theoretical analysis of optimal free responses[J]. Neural Computation, 2003, 15(9): 2147-2177. DOI:10.1162/089976603322297331 |
| [20] |
WISKOTT L, SEJNOWSKI T J. Slow feature analysis:Unsupervised learning of invariances[J]. Neural Computation, 2002, 14(4): 715-770. DOI:10.1162/089976602317318938 |
| [21] |
LEE J M, YOO C K, LEE I B. Statistical process monitoring with independent component analysis[J]. Journal of Process Control, 2004, 14(5): 467-485. DOI:10.1016/j.jprocont.2003.09.004 |
| [22] |
DOWNS J J, VOGEL E F. A plant-wide industrial process control problem[J]. Computers & Chemical Engineering, 1993, 17(3): 245-255. |
| [23] |
LYMAN P R, GEORGAKIS C. Plant-wide control of the Tennessee Eastman problem[J]. Computers & Chemical Engineering, 1995, 19(3): 321-331. |




