2. 常州大学 江苏省绿色过程装备重点实验室,江苏 常州 213164
2. Jiangsu Key Laboratory of Green Process Equipment, Changzhou University, Changzhou 213164, China
小颗粒污染物是城市雾霾的罪魁祸首,从排放源上对其进行治理是解决空气问题的主要途径。静电除尘器、布袋除尘器等传统设备对粒径大于5 μm的小颗粒已有很高的除尘效率,然而随着粒径的减小,去除效率也逐渐降低,当粒径小于2.5 μm时,去除效率甚至会低于50%[1]。采用凝并法提高小颗粒的去除效率是一种较新的技术发展趋势。
湍流凝并是一种简单高效的凝并技术,已被广泛地应用于细颗粒物排放控制中。通常在流场基础上施加电场,通过库仑力进一步提高除尘效率,结果却使系统复杂化,用电量增大。陈亚伟[2]和刘含笑[3]在凝并装置内增加扰流板和扰流柱,通过改善流场增大碰撞概率,从而提高凝并效率,但改造后结构复杂,安装困难,优化效果也不明显。刘定平[4]提出一种切圆式旋流凝并装置,通过研究颗粒运动轨迹,发现旋流有利于细颗粒的混合和碰撞,但在研究旋流场对凝并过程的影响时,没有得出一个恰当的凝并核模型,因而不能直观地得出旋流对凝并效果的影响规律。TEICHMANN等[5]提出一个应用于喷射流的湍流凝并模型。PESMAZOGLOU[6]对湍流凝并模型进行改善,提出一个无需对流场进行预定义的通用湍流模型,LEE[7]通过拟合布朗凝并和湍流凝并,得出一个理论上更符合实际的凝并模型。以上研究未考虑颗粒的破碎,而HARSHE[8]在研究颗粒凝并过程时提出,剪切流引起的剪切效应会导致较大微米级颗粒的破碎,XIAO[9]进而提出了一个剪切破碎核函数。此外,徐挺等[10]采用气液交叉流系统对粒径0.2~10 μm的颗粒物进行了脱除实验,结果表明脱除效率随粒径增大而增大,所以对亚微米级及以上粒径小颗粒凝并过程进行研究具有一定的意义。
为得到旋流对颗粒凝并的直观影响,本文建立一种适用于湍流场且考虑剪切破碎影响的凝并核模型,研究旋流场对亚微米级及微米级颗粒凝并效果的影响。湍流对纳米级颗粒碰撞的影响尺度极小,所以不考虑旋流对纳米级颗粒凝并影响。
2 颗粒运动凝并模型 2.1 颗粒控制方程描述颗粒扩散、凝并及破碎动力学特性的颗粒控制方程为[11-12]:
| $\begin{gathered} \frac{{\partial n\left( {v, x, t} \right)}}{{\partial t}} + u\left( {x, t} \right)\nabla n\left( {{v_0}, x, t} \right) - \nabla \left[ {D\nabla n\left( {{v_0}, x, t} \right)} \right] = \\ \frac{1}{2}\int_\mathit{0}^{{v_0}} {\beta \left( {v, {v_0} - v} \right)} n\left( {v, x, t} \right)n\left( {{v_0} - v, x, t} \right)\text{d}v \hfill \\ - n\left( {{v_0}, x, t} \right)\int_{{v_0}}^\infty {\beta {{\left( {v, {v_0}} \right)}_{}}} n\left( {v, x, t} \right)\text{d}v + {\int_{{v_0}}^\infty {s\left( v \right)} _{}}n\left( {v, x, t} \right)\\ b\left( {{v_0}, v} \right)\text{d}v - s\left( {{v_0}} \right)n\left( {{v_0}, x, t} \right) \hfill \\ \end{gathered} $ | (1) |
等式右边第1、2项为凝并项;第3、4项为破碎项,n为颗粒浓度函数,D为扩散系数,
扩散系数D包含分子扩散系数Dm和湍流扩散系数Dt两部分,即:
| $D=D_{\text{m}}+D_{\text{t}}$ | (2) |
湍流施密特数Sct是影响湍流扩散系数的重要参数,即:
| $D_{\text{t}}=\frac{\mu_{\text{t}}}{\rho S c_{\text{t}}}$ | (3) |
YIMER等[13-14]研究发现,采用k-ε 模型时,湍流施密特数Sct取0.7~0.9时模拟结果接近实验结果,因此本文湍流施密特Sct数取0.7。
2.2 凝并核函数凝并核函数
| $\beta = \alpha K$ | (4) |
凝聚效率
| $\alpha = {\left( {\frac{{0.242{d_{\rm{p}}}}}{{0.242{d_{\rm{p}}} + 50.37\varepsilon }}} \right)^{0.233}}$ | (5) |
本文研究的是旋流对小颗粒凝并效果的影响,主要考虑布朗凝并和湍流凝并,两种凝并形式对于颗粒碰撞的影响尺度不同,因此认为两者是相互独立的[16],叠加后的碰撞核函数:
| $K = {\left( {K_{\rm{b}}^2 + K_{\rm{t}}^2} \right)^{\frac{1}{2}}}$ | (6) |
Kb为布朗碰撞核,Kt为PESMAZOGLOU[6]湍流碰撞核。采用GMACHOWSKI[17]提出的基于拟合连续区和自由分子区的碰撞核函数:
| ${K_{\rm{b}}} = \frac{{2\pi {{\left( {{a_i} + {a_j}} \right)}^3} \times \left( {\pi fKn_{\rm{D}}^2} \right)}}{{4m + 2\pi K{n_{\rm{D}}}m}}$ | (7) |
该碰撞核函数适用于全粒径范围,通过FUCHS [18]实验验证了其准确性。式(7)中的Kundsen数KnD是为简化公式而定义的无量纲数:
| $ K{n_{\rm{D}}} = \frac{{1 + {D_j}/{D_i}}}{{\left( {1 + {a_i}/{a_j}} \right)\sqrt {1 + u_j^2/u_i^2} }}\frac{{{\lambda _i}}}{{{a_j}}} $ | (8) |
本文研究的颗粒粒径范围在0.1~20 μm,当颗粒粒径大于10 μm时,剪切应力与颗粒的自保持力(即保持小颗粒原有形状的黏性力)达到同样的量级,此需考虑颗粒的破碎。为方便计算,认为影响流场中凝并和破碎的因素包括两方面[19],一是凝并颗粒的固有特征,如黏性强度和颗粒大小,二是求解域的物理特性,比如剪切应力。引入一个由XIAO[9]提出的描述破碎率的表达式
| $S = EG\exp \left( { - \frac{\sigma }{\tau }} \right)\frac{{{L_{\rm{i}}}}}{{{L_{\rm{s}}}}}$ | (9) |
定义一个和剪应力以及内部黏性力有关的无量纲破碎概率Prob[20]:
| $Prob = \exp \left( {\frac{{ - \sigma }}{\tau }} \right)$ | (10) |
式中
| $\sigma = \left( {\frac{9}{8}} \right){k_c}\mathit{\Phi} F\left( {\frac{1}{{\pi d_0^2}}} \right)$ | (11) |
式中
| ${F_{\rm{v}}} = \frac{{A{d_0}}}{{12{h^2}}}$ | (12) |
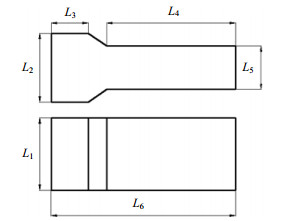
为验证算法,首先参考徐俊波[21]的实验,其凝并装置结构如图 1所示。对其划分六面体网格,总数为84 240。
|
图 1 实验对比凝并装置结构 Fig.1 Schematic diagram of the agglomeration unit used in experimental comparison |
本文采用的旋流凝并装置结构如图 2所示,含小颗粒气体沿轴向进入凝并室,不含颗粒物的气体由两处切向入口进入并产生旋流,为了延长细颗粒物在凝并室内的停留时间,凝并室的管径大于入口直径,由一个锥形扩散通道与轴向入口连接,出口为圆形,由一个锥形收缩段与凝并室连接,计算域网格数为89 401。在设置旋流的基础上,参照陈亚伟[2]的方法,在旋流器内部添加4片均匀分布的轴向扰流板,并开设半圆形槽孔,使颗粒随气流作径向运动,如图 3所示。

|
图 2 旋流凝并装置结构 Fig.2 Schematic diagram of the swirling coagulation unit |

|
图 3 扰流板结构 Fig.3 Schematic diagram of the spoiler |
|
|
表 1 凝并装置结构尺寸(mm) Table 1 Structural dimensions of the coagulation unit (mm) |
由于凝并器中的颗粒数量通常在1014以上,而DEM (Discrete Element Method)方法一般适用于颗粒数量少于1010的离散相系统。当颗粒数量大时,采用DPM (Discrete Phase Model)追踪每个颗粒的运动轨迹也非常困难,且DPM模型往往只可以得到颗粒的运动轨迹,并不能给出颗粒的碰撞频率及凝并效果等信息。因此,本文采用计算量较小且能描述碰撞频率和碰撞效果等信息的群体平衡模型(Population Balance Model)模拟凝并器中单分散小颗粒的凝并情况。群体平衡模型通过对小颗粒进行跟踪,把小颗粒的凝并、破碎等微观行为与小颗粒粒径、面积等宏观属性联系起来,是研究离散相凝并行为的有效工具,颗粒控制方程采用均相离散法进行计算,流场采用RNG k-ε湍流模型进行计算。
3.3 边界条件实验工况和计算边界条件如表 2所示。
|
|
表 2 边界条件 Table 2 Boundary conditions used in the study |
实验和数值模拟出口粒径分布如图 4所示。

|
图 4 模拟、实验结果对比 Fig.4 Comparison of experimental and simulation results |
考虑到小颗粒采样、粒径测量、外部空气环境等误差来源,以及0.5 μm的聚苯乙烯微球基本不可能出现破碎的情况,对试验中出现的粒径低于0.5 μm的情况不予考虑,经计算,在去除小于0.5 μm的颗粒后,试验结果平均粒径为0.759 μm,模拟结果平均粒径为0.823 μm。数值和实验的粒径峰值都出现在0.6~0.7 μm,颗粒分布情况基本相似,因此认为数值方法是可靠的。
4.2 旋流对小颗粒运动的影响图 5所示为轴向流速0.5 m·s-1时无旋流和带1 m·s-1切向进气两种情况下,1 μm颗粒的运动轨迹。添加旋流后,颗粒顺着管壁作螺旋运动,促进了不同原始位置处小颗粒的混合,延长了运动轨迹;旋流入口处产生入口涡流,促进颗粒碰撞。

|
图 5 颗粒运动轨迹 Fig.5 Profiles of particulate movement trajectory |
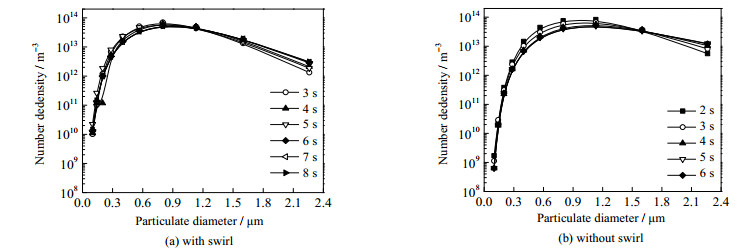
由于初始颗粒粒径为0.1 μm,内部黏性力与剪切应力不在一个数量级,颗粒粒度远小于颗粒发生破碎的粒度[22],所以暂不考虑破碎对凝并的影响,同时因为颗粒粒度为亚微米级,所以忽略颗粒相对连续相的影响。不同时刻出口粒径分布如图 6所示。
|
图 6 亚微米级颗粒不同时刻出口粒径分布 Fig.6 Profile of submicron particulate diameter distribution at exit |
对比出口粒径分布情况,无旋流情况下,颗粒系统在到达出口后的第5 s时达到较稳定状态,即该流况下的颗粒系统自保持状态,而有旋流的小颗粒系统则在到达出口后的第7 s逐渐趋于稳定,可见颗粒系统在无旋流的情况下能更快达到稳定状态,而颗粒系统达到其流况下的自保持状态时,无旋流情况下大于1 μm的颗粒数量远大于旋流处理后的颗粒数量,所以无旋流情况下的颗粒平均粒径更大。
对于亚微米级颗粒,气体介质的非连续性效应对颗粒的行为有较大影响,颗粒受到的空气阻力相对较小,颗粒拥有较大的扩散速度,其布朗凝并效率也较高,所以在无旋流情况下就能获得较高的凝并效率。旋流的加入一方面增强了粒子富集效应,延长了颗粒的运动轨迹,另一方面也影响了颗粒由高浓度向低浓度的自由扩散,同时,旋流有助于分离不同大小的颗粒,粒径越大的颗粒越靠近管壁,使颗粒随着气流作规则的螺旋运动,大大减小了粒径比较大的颗粒之间的碰撞概率,从而降低了凝并效率。
4.4 旋流场对微米级颗粒凝并的影响在研究旋流对微米级颗粒凝并的影响时,颗粒初始粒径设为1 μm,为确保凝并室内的颗粒数量密度大于1014 m-3,轴向入口处采用0.002的体积分数,考虑到微米级颗粒达到可破碎粒度,模拟中考虑剪切破碎对颗粒场的影响,其他条件不变。对有旋流和无旋流的微米级颗粒凝并过程进行模拟,设定旋流流速为0.1 m·s-1,出口粒径分布如图 7所示。

|
图 7 微米级颗粒不同时刻出口粒径分布 Fig.7 Profile of micron particulate diameter distribution at exit |
无旋流时颗粒凝并效率随时间逐渐增加,在颗粒达到出口的第6 s,颗粒分布逐渐趋于平稳,达到自保持状态。有旋流处理时,细颗粒在第7 s达到该流况下的凝并最佳效果,随后粒径大于10 μm的颗粒数量小幅度降低,并达到该流况下的自保持状态,其凝并效果略小于无旋流处理的气溶胶系统。
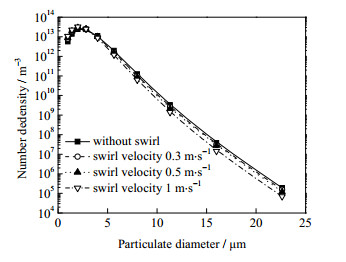
对比不同旋流速度下的颗粒系统,达到自保持状态后的出口粒径分布如图 8所示,有旋流和无旋流两种情况下的粒径峰值均在2~3 μm,但加入旋流会使粒径减小,且旋流速度越大,粒径越小。
|
图 8 不同旋流流速处理的颗粒出口粒径 Fig.8 Profiles of particulate diameter distribution at exit under different swirl rates |
对于微米级颗粒,气体介质可视为连续,颗粒扩散阻力较大,自由扩散碰撞凝并概率降低,湍流导致的颗粒凝并成为影响粒径变化的重要因素,所以相比亚微米级颗粒,有旋流与无旋流的颗粒分布情况更相近,但旋流也会导致不同粒径小颗粒的分离,且旋流流速越快分离效果越明显,从而大大减少了凝并室后半段粒径比较大的颗粒之间的碰撞(粒径比越大碰撞效率越高)。由于旋流的存在,剪切效应加剧,有可能出现作用在聚合体上的剪切力大于黏合力(范德华力或键合力)的情况,导致颗粒的剪切破碎,所以有旋流的平均粒径较无旋流的平均粒径更小。
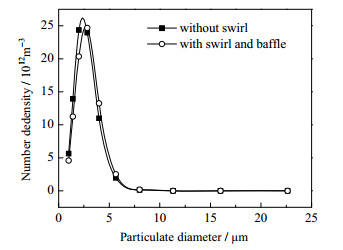
相比亚微米级颗粒,旋流处理的微米级颗粒凝并效果与单轴向进气处理颗粒凝并效果更接近,所以在添加扰流板的基础上再对微米级颗粒进行模拟,设定轴向气流流速为0.5 m·s-1,旋流流速为0.5 m·s-1,颗粒系统达到稳定状态后,其出口粒径分布情况如图 9所示。
|
图 9 颗粒出口粒径分布 Fig.9 Particulate diameter distribution at exit |
对比出口处粒径分布情况,在旋流的基础上添加轴向扰流板后,颗粒平均粒径略大于无旋流情况下颗粒粒径,但粒径大于10 μm的颗粒数量较无旋流情况下更少。
在旋流的基础上添加扰流板,能使较大颗粒向远离壁面的方向移动,促使其与较小颗粒的碰撞,达到增强凝并的目的,而旋流导致的剪切强度的增加同样导致了粒径大于10 μm的颗粒的破碎。
5 结论本文建立了一个颗粒凝并模型并与前人实验结果对比,验证了模型的可靠性,并以此研究旋流对亚微米级及微米级颗粒凝并效果的影响,主要结论如下:
(1) 对于亚微米级颗粒,布朗凝并是促成颗粒凝并的主导因素,旋流场的增加反而影响了颗粒的自由扩散,从而降低了凝并效率。
(2) 对于微米级颗粒,湍流程度是影响颗粒凝并的重要因素,所以旋流场的增加在一定程度上促进了颗粒的凝并,但同时也促进了不同粒径颗粒的分离,旋流流速越大,凝并效果越差,而由旋流导致的剪切流也会在一定程度上减小大粒径颗粒的数量,所以旋流的增加并不能直接促颗粒的凝并。
(3) 在添加旋流的基础上增加扰流板,在延长小颗粒运动轨迹的基础上,迫使外围的大颗粒向中心移动,增大不同粒径颗粒之间的碰撞,从而改善凝并效果。
符号说明:
|
|
| [1] |
张会君, 卢徐胜. 控制PM2.5的除尘技术概述[J]. 中国环保产业, 2012, 3: 29-33. ZHANG H J, LU X S. Explication on controlling PM2.5 precipitation technology[J]. China Environmental Protection Industry, 2012, 3: 29-33. |
| [2] |
陈亚伟, 熊扬恒, 周建龙, 等. 凝并元件结构优化对气固两相流流场及颗粒凝并效果的影响[J]. 热力发电, 2016, 45(1): 60-64. CHEN Y W, XIONG Y H, ZHOU J L, et al. Influence of coagulation element structure optimization on gas-solid two-phase flow field and particulate coagulation[J]. Thermal Power Generation, 2016, 45(1): 60-64. DOI:10.3969/j.issn.1002-3364.2016.01.060 |
| [3] |
刘含笑, 姚宇平, 郦建国, 等. 凝聚器二维单扰流柱流场中颗粒凝并模拟[J]. 动力工程学报, 2015, 35(4): 292-297. LIU H X, YAO Y P, LI J G, et al. Coagulating simulation of particles in flow field of coagulator 2D single turbulence column[J]. Journal of Chinese Society of Power Engineering, 2015, 35(4): 292-297. |
| [4] |
刘定平, 罗伟乐. 基于旋流与声波的颗粒复合凝并建模与运动轨迹仿真[J]. 动力工程学报, 2017, 37(5): 413-417. LIU D P, LUO W L. Moving trajectory simulation of particles and modeling of the complex coagulation based on swirl and acoustic wave[J]. Journal of Chinese Society of Power Engineering, 2017, 37(5): 413-417. |
| [5] |
TEICHMANN J, BOOGAART K G VAN DEN. Cluster models for random particle aggregates — Morphological statistics and collision distance[J]. Spatial Statistics, 2015, 12: 65-80. DOI:10.1016/j.spasta.2015.03.002 |
| [6] |
PESMAZOGLOU I, KEMPF S, NAVARRO-MARTINEZ. Large eddy simulation of particle aggregation in turbulent jets[J]. Journal of Aerosol Science, 2017, 111: 1-17. DOI:10.1016/j.jaerosci.2017.06.002 |
| [7] |
LEE S H. Numerical study of aggregation and breakage of particles in taylor reactor[J]. Transactions of the Korean Society of Mechanical Engineers B, 2016, 40(6): 365-372. DOI:10.3795/KSME-B.2016.40.6.365 |
| [8] |
HARSHE Y M, LATTUADa M. Breakage rate of colloidal aggregates in shear flow through stokesian dynamics[J]. Langmuir, 2012, 28(1): 283-292. DOI:10.1021/la2038476 |
| [9] |
FENG X, HUI X, XIAO Y L, et al. Modelling particle-size distribution dynamics in a shear-induced breakage process with an improved breakage kernel: Importance of the internal bonds[J]. Colloid s and Surfaces, 2015, 468: 87-94. DOI:10.1016/j.colsurfa.2014.11.060 |
| [10] |
徐挺, 魏文韫, 孙白宇, 等. 气液交叉流脱除亚微米级颗粒物的研究[J]. 高校化学工程学报, 2017, 31(4): 960-969. XU T, WEI W Y, SUN B Y, et al. Study on sub-micron particle removal by gas-liquid cross-flow array systems[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(4): 960-969. DOI:10.3969/j.issn.1003-9015.2017.04.029 |
| [11] |
SMOLUCHOWSKI M V. Experiments on a mathematical theory of kinetic coagulation of colloid solution[J]. Zeitschrift Fur Physikalische Chemie-Stochiometrie Und Verwandtschaftslehre, 1992, 2: 1777-1786. |
| [12] |
BANHELMES G, PRATSINIS S E, BUGGISCH H. Particle size distributions and viscosity of suspensions undergoing Shear-induced coagulation and fragmentation[J]. Chemical Engineering Science, 2003, 58(13): 2893-2902. DOI:10.1016/S0009-2509(03)00133-7 |
| [13] |
YIMER I, CAMPBELL I, JIANG L. Estimation of the turbulent Schmidt number from experimental profiles of axial velocity and concentration for high-reynolds-number jet flows[J]. Canandian Aeronautics and Space Journal, 2002, 48(3): 95-200. |
| [14] |
LAW A W K. Velocity and concentration distributions of round and plane turbulent jets[J]. Journal of Engineering Mathematics, 2006, 56(1): 69-78. |
| [15] |
HO C A, SOMMERFELD M. Modelling of micro-particle agglomeration in turbulent flows[J]. Chemical Engineering Science, 2002, 57(15): 3073-3084. DOI:10.1016/S0009-2509(02)00172-0 |
| [16] |
FLAGAN R C, SAROFIM A F. Coal generated inorganic aerosol: A review[C]. First international Aerosol Conference, 1984, 23(4): 778-782.
|
| [17] |
GMACHOWSKI L. The aerosol particle collision kernel considering the fractal model of particle motion[J]. Journal of Aerosol Science, 2013, 59: 47-56. DOI:10.1016/j.jaerosci.2013.02.002 |
| [18] |
FUCHS N A, SUTUGIN A G. Hihgly dispersed aerosols[M]. London: Ann Arbor Science Publishers, 1970.
|
| [19] |
XIAO F, LI X Y. Modelling the kinetics of aggregate breakage using improved breakage kernel[J]. Water Science and Technology, 2008, 57(1): 151-157. DOI:10.2166/wst.2008.789 |
| [20] |
ODRIOZOLA G, SCHMITT A, MONCHO-JORDA A, et al. Constant bond breakup probability model for reversible aggregation processes[J]. Physical Review E, 2002, 65(3): 151-156. |
| [21] |
徐俊波, 张丽, 岳仁亮, 等. PM2.5细颗粒物凝并的计算流体力学模拟[J]. 计算机与应用化学, 2013, 30(80): 831-834. XU J B, ZHANG L, YUE R L, et al. Computational fluid dynamics simulation of coagulation of PM2.5 fine particles[J]. Computers and Applied Chemistry, 2013, 30(80): 831-834. |
| [22] |
PATRUNO L E. Analysis of breakage kernels for population balance modelling[J]. Chemical Engineering Science, 2009, 64: 501-508. DOI:10.1016/j.ces.2008.09.029 |




