2. 西安交通大学 计算机科学与技术系, 陕西 西安 710049;
3. 热流科学与工程教育部重点实验室, 陕西 西安 710049
2. Department of Computer Science and Technology, Xi'an Jiaotong University, Xi'an 710049, China;
3. Key Laboratory of Thermo-Fluid Science and Engineering, Ministry of Education, Xi'an 710049, China
化工过程系统中的很多优化问题都可以归结为一个复杂的混合整数非线性规划模型[1](Mixed-integer Nonlinear Programming,MINLP)。而换热网络是其中研究最早,也是非凸非线性最严重的系统之一[2]。模型本身的非凸性、非线性和不连续性,使得这类优化问题的求解极为困难[3]。目前,可求解这类优化问题的算法主要分为确定性和随机性算法两大类。Grossmann[4]对求解MINLP问题的确定性算法进行了详细的总结。他指出确定性算法获得问题全局最优解往往是以执行时间为代价的。加之确定性算法的求解时间与待求问题的复杂度直接相关。因此,随着优化问题规模的不断扩大,确定性算法将难以直接应用于实际优化问题的求解中。与此相反,随机性算法作为一种黑箱算法,却因其良好的鲁棒性和易于执行的特征,使其在求解复杂优化问题中得到了广泛的应用[5]。
遗传算法(Genetic Algorithm,GA)是目前应用最广泛的随机类算法之一[6]。而如何进一步提高遗传算法的性能成为了研究者们关注的重点。Ponsich等人[7]采用GA求解间歇过程设计的MINLP优化模型时发现对于同时存在整型变量和连续变量的优化问题,应该采用混合编码方式。基于此发现,Danish等人[8]在基本遗传算法中引入了锦标赛选择、SBX交叉和多项式变异等遗传操作,并通过增加精英策略和动态罚提高了算法性能。与此类似,Young等人[9]也将信息理论、局部搜索算法以及自适应罚函数运用到遗传算法中,进一步提高了GA的求解效率。然而,上述研究均是在串行环境下实现的,改进后算法可求解问题的复杂度和规模仍然受限。
为此,很多研究者将目光投向了近年来备受关注的图形处理器(Graphics Process Unit,GPU)。因为GPU优异的数据处理性能和低成本,可以为扩大GA在实际中的应用规模提供机会[10]。Yu等人[11]分析了在GPU上实施GA的优势。Wong等人[12]成功实现了GA在GPU上的并行化,并且提出了一种基于GPU的多目标进化算法[13]。然而,这些研究只关注了并行化对算法求解效率的影响,却忽略了并行计算过程中对设备的优化和有效利用。Munawar等人[14]构建了基于GPU的自适应GA用于求解复杂的MINLP和NLP问题。他们还通过引入信息熵算法和局部搜索技术进一步提高了算法性能。数值实验的结果表明该并行GA的收敛性和加速效果显著。然而,为了简化算法的并行过程,他们仅对整个算法中最耗时的自适应求解过程和局部搜索操作2部分进行了并行化处理,并未充分利用GA本身的并行计算优势;另一方面,该并行GA是在单CPU和GPU卡的计算条件下完成,计算中仅利用了GPU的并行加速功能;此外,已有的整个并行GA中GPU端核函数的划分不够细致,致使每个GPU核上承担的计算任务过重,程序访问显存的时延长。
针对以上问题,在充分分析GA本身的并行计算特征的基础上,作者提出了基于OpenMP的并行GA。该算法不仅实现了CPU线程和GPU线程的同步并行加速,而且通过更细致的核函数划分最大限度地减少了访问时延。本文以换热网络优化问题为例,验证了方法的有效性。通过本文计算结果与文献结果的比较,验证算法的准确性;通过串并行GA求解时间的对比,阐明了本文并行算法的求解效率。
2 改进GA的并行化设计GA的基本思想是通过种群生成,杂交,变异和选择等一系列遗传操作实现种群的不断进化以获得最终解。核心是保持优秀个体的优越性,直至收敛。为了解决基本GA收敛慢,且极易陷入局部最优解的问题,实际中往往需要加入一系列的控制或调整策略来引导基因的走向,以有效地保留优秀基因。因此,本节中首先采用Munawar等人[15]提出的一系列优化和控制策略对基本GA进行改进,然后通过分析算法的特征实现算法的并行化。
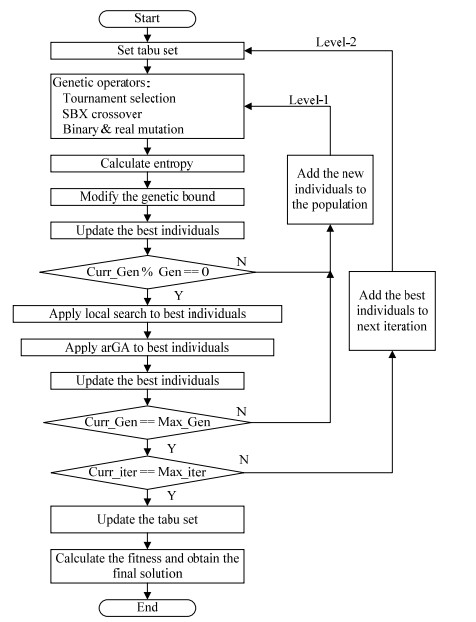
2.1 改进的GA图 1是改进后的GA流程。由图可见,本文对Munawar等人[15]所提出的遗传算法进行了分级处理。改进后的GA共有两级,第二级是由若干次第一级迭代构成。在第一级迭代过程中,通过实施遗传操作和一系列的基因控制和调整策略,保持个体基因的优越性,并将优秀个体进行保存。一级迭代结束后,程序都将返回第二级,进行下一段一级迭代。同时上一段一级迭代中保存的优秀个体将作为下一段一级迭代过程的初始种群。如此反复就使得个体的最优性随着迭代的进行而不断提升。
|
图 1 改进后的GA流程 Fig.1 The flow diagram of improved genetic algorithm |
相比Munawar等人[15]提出的GA流程,本文还加入了禁忌集和相应的禁忌准则来避免迂回搜索,并通过藐视准则来赦免一些被禁忌的优秀个体,进而保证了个体基因的多样化。因此,改进后的GA更加注重求解过程中优秀个体的选择、进化和保存,提高了获得全局最优解的概率。
2.2 改进GA的并行化设计为了便于分析,将1.1节中GA所包含的所有操作分为独立操作和共用操作。独立操作如种群的生成,个体的交叉和变异,信息熵计算,适应度函数计算,基因上下限调整,局部搜索等相互独立的操作,这些操作都是针对独立的个体进行,彼此之间互不干扰。因此,这些过程可直接移植到GPU上执行。而GA中的共用操作主要包括随机数的生成和排序操作两类。算法中种群的进化和个体的遗传操作,如种群的生成、个体的杂交、变异以及自适应求解的遗传算法都需要产生大量的随机数,耗时很长。考虑到以上所有的随机操作都是针对种群中多个独立个体同时进行,这一特征使得遗传算法中所有随机数的生成过程均可通过GPU实现并行执行。除此之外,GA中基因池和候选集的更新都需要首先对种群进行排序以获取优秀个体,该排序过程也可方便地移植到GPU上实施。综上所述,算法中涉及的各类操作,不论是基本操作还是共用操作,都可方便地在GPU上并行实现。
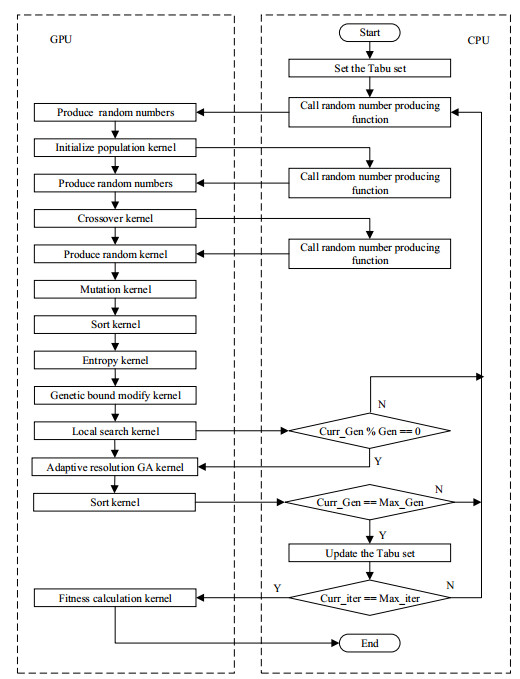
基于以上分析,得到如图 2所示的并行GA在CPU和GPU上的任务分配图。由图 2可知,本文提出的并行GA是一种在CPU-GPU异构计算系统下的并行算法。除判断和循环操作在CPU上执行外,该算法的其他基本操作均在GPU上以调用端核函数的形式实现并行化。
|
图 2 GA中CPU和GPU任务分配 Fig.2 Task assignment to CPU and GPU in parallel GA |
图 2中还显示该GA中共包含了9个端核函数。除Munawar等人[15]研究中涉及的核函数外,本文增加的核函数及其功能包括:排序核函数主要负责种群排序,并同时完成基因池和候选集的更新。基因上下限调整核函数主要负责对基因位落入概率进行查询,得出每个基因位最大的概率位置,寻找合适位置并调整基因范围;需要特别指出的是,GPU端随机数的产生函数只能在CPU端调用,而随机数的生成是在GPU实现的。
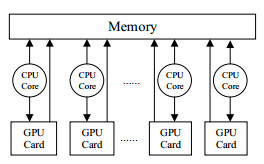
3 基于OpenMP系统的并行GA 3.1 共享内存的并行计算系统分析图 3是共享内存并行计算系统(Open Multiprocessing, OpenMP)的示意图。OpenMP是一种基于共享内存的多线程程序设计方法。该系统包含多个CPU核心和多个GPU卡,所有CPU和GPU共享一个主存,而其中的多个CPU核心可共享内存,而多个GPU卡之间不存在内存共享。OpenMP系统中每个CPU线程负责控制一个GPU卡,包括计算任务分配、显存分配、线程划分和核函数启动等。当GPU完成分配的计算任务后,将计算结果汇总至对应的CPU核心,然后合并所有CPU线程,返回问题的最终解。
|
图 3 共享内存的并行系统示意图 Fig.3 A sketch for open multiprocessing system |
本文采用OpenMP设计框架进行求解的主要原因在于该系统不但确保了GPU端和CPU主线程端计算任务的同步并行化,而且实现了CPU主线程和GPU卡的一对一控制,既能有效提高计算并行度,又能充分利用CPU和GPU的计算资源。本文在计算的过程中用到了2个CPU核心和2块GPU卡,计算环境为:CPU为Intel®Xeon5600 2.93 GHz,GPU为nVidia Tesla C2050,内存3 GB,共有448个核;操作系统是Cent-OS 6.0 x8664和CUDA SDK/Toolkit Ver. 4.0。
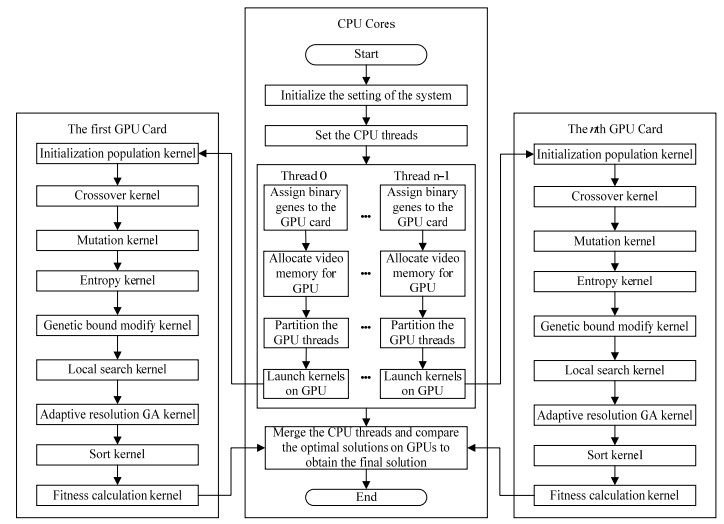
3.2 基于OpenMP的并行GA根据图 2中并行GA流程和OpenMP并行计算系统的说明,得到了基于OpenMP系统的并行GA流程,如图 4所示。该算法流程的主要步骤如下:
|
图 4 基于OpenMP的并行GA流程 Fig.4 The flowchart of the parallel genetic algorithm based on OpenMP |
(1)初始化设置。CPU通过单线程运行获取系统中的GPU数量,并完成CPU线程个数设置以及CPU和GPU线程的初始设置;
(2) CPU的多线程化设置。每个CPU负责控制一个GPU卡上的显存分配,线程划分、核函数启动等任务。同时将模型中的二进制基因分配给对应的GPU。本文中二进制基因空间的分配是按照GPU板卡的数量均匀划分的。
(3) CPU-GPU异构并行求解。按照图 2中CPU和GPU的任务分配情况完成各自的计算任务,获得每个GPU候选集中的最优解;
(4) CPU多线程合并。将每个GPU上的最优解传输到CPU上后,由CPU单线程完成最优解的筛选,输出最优解,并终止运算。
需要说明的是本文提出的并行GA只是对原有串行GA的一种改进,仍具备串行GA通用性的特征。
4 基于OpenMP的并行GA在换热网络优化中的应用为了验证基于OpenMP的并行GA的正确性和有效性,本节将该算法用于文献中2个规模不同的换热网络优化问题的求解。计算采用的换热网络优化模型为Yee和Grossmann[2]提出的分级超结构模型。换热网络的设计目标是达到最小的年总费用,即换热网络的能量费用、固定费用以及换热面积费用三者的加和最小。在计算硬件环境一致的条件下,将2个换热网络设计实例分别采用串行和并行GA求解,并对两种执行方式下所得的计算结果和执行时间进行比较和分析,以说明基于OpenMP的并行GA的加速效果。
4.1 换热网络基础数据案例A来源于Zamora and Grossmann[16]的文章,该网络包括2个冷流和2个热流。加热公用工程是177℃的蒸汽,冷却公用工程是进出口温度分别为20和40℃的冷却水。冷热公用工程的年度化费用分别为80和20 $·kW-1。加热器和其他换热单元中流股的总传热系数分别取1.2和0.8 kW·m-2·℃-1。
换热单元的年度化费用($·a-1)可以按照下式进行计算:
对于加热器:6250 + 83.26A
其余换热单元:6250 + 99.91A
案例B来自Ciric和Floudas[17]的文章。该案例中包括4个热流股和3个冷流股。该模型规模比案例A有所增大。该例中,热公用工程的温度为300℃,单价为80 $·(kW·a)-1。冷却公用工程的进出口温度分别为70℃和90℃,冷公用工程的单价按照20 $·(kW·a)-1进行计算。该案例中所有流股之间的匹配采用统一的总传热系数0.8 kW·m-2·℃-1,换热单元的年总投资费用按1300A0.6计算。
4.2 计算结果的对比与分析为便与比较,以上2个案例中选取的最小传热温差与超结构模型的分级数均与文献中保持一致。采用本文提出的并行GA计算以上2个换热网络优化设计案例,所得结果与文献中结果的对比分别列于表 1和表 2中。
| 表 1 案例A的计算结果对比 Table 1 Comparison of results obtained in this work and those in literature for Case A |
| 表 2 案例B的计算结果对比 Table 2 Comparison of results obtained in this work and those in literature for Case B |
对于案例A,表 1中Zamora和Grossmann[16]的最优解是通过求解无分流的换热网络分级超结构模型获得的。Pariyani等人[18]采用随机算法分别在无分流和有分流的情况下得到了比Zamora和Grossmann[16]更好的结果。类似地,Yerramsetty等人[19]采用微分进化算法也分别在无分流和有分流两种情况下得到最优换热网络设计方案。他们的计算结果都表明该案例中允许流股分流可获得更低的年总费用。因此,本文在考虑流股分流的情况下分别采用串行GA和并行GA对该换热网络进行优化。计算结果表明,串行GA和并行GA所得的计算结果是一致的,且所得换热网络的年总费用为$84, 840,该结果优于文献中所得结果。因此,可以认为本文提出的并行GA可以获得该换热网络的最优解。
对于案例B,由表 2中可知,虽然本文设计方案中换热网络的操作费用较高,但相比于其他结果,本文运用并行GA所得换热网络的结构更简单,投资费用更低,最终的年总费用也明显优于文献中给出的结果。因此,对于该换热网络设计问题而言,本文的并行GA可获得比文献中更优的结果。
综合以上结果分析可知,本文提出的并行GA可获得比文献中更优的换热网络设计方案。这不但验证了并行GA求解的准确性,也说明本文针对GA的改进是合理且有效的。
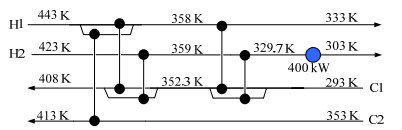
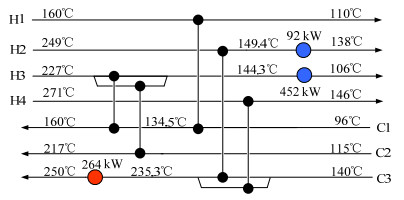
图 5和图 6分别给出了本文所得到的以上两个换热网络实例的最优换热网络结构。该结构与文献中给出的最优结构具有相同数量的换热器数目,但流股的匹配关系不同。而图 6中所得换热网络设计方案相比于文献中给出的方案包含的换热器个数更少,网络结构也更加简单。
|
图 5 并行GA得到的案例A的最优换热网络结构 Fig.5 The optimal HEN structure of Case A obtained by the proposed paralleled GA |
|
图 6 并行GA得到的案例B的最优换热网络结构 Fig.6 The optimal HEN structure of Case B obtained by the proposed parallel GA |
为了研究并行GA的加速特性,表 3中给出了2个案例规模的对比以及串行和并行GA求解时间的对比。
| 表 3 2个换热网络实例中串并行GA的求解时间对比 Table 3 Comparison of executive times in sequential and parallel GA for two examples |
由表 3可知,本文提出的并行GA相比于串行GA具有明显的加速效果。对于规模较小的案例A而言,求解时间的加速比大于10,而对于规模稍大的案例B而言,求解时间的加速比也接近30。也就是说,并行GA的加速比随着换热网络优化问题规模的增大而增大。这与作者之前研究中所得的结论是一致的,即GPU并行加速算法的优势将随着求解问题规模的增大而不断凸显[10]。这一特征将有利于大规模换热网络优化问题的快速准确求解。
5 结论为提高化工过程系统优化问题的求解效率,本文提出了基于OpenMP计算平台的并行遗传算法。该算法在基本遗传算法的基础上加入了一系列调整和控制策略,用以提高算法的全局寻优性和收敛性。除此之外,作者还对该算法的计算流程进行了分析,实现了改进后算法在OpenMP系统下的并行化设计,完成了CPU主线程和GPU多线程的同步并行化目标。以换热网络优化问题为例,验证了本文方法的有效性。计算结果表明,基于OpenMP的并行GA不但能够获得优于文献中结果的换热网络设计方案。相比于串行的GA,并行GA的加速效果显著,且加速比随着换热网络问题规模的增大而增大。这一特征对于快速准确的求解化工系统中实际的大规模优化问题具有重要意义。
然而,本文中所选取的案例规模离实际生产还有差距,作者将在此基础上,进一步研究影响并行GA加速特性的因素,以期进一步扩大并行GA可求解问题的规模。
| [1] | WANG Yu-fei(王彧斐), FENG Xiao(冯霄) . Progress on heat exchanger network synthesis and optimization(换热网络集成与优化研究进展)[J]. Chemical Reaction Engineering and Technology(化学反应工程与工艺) , 2014, 30 (3) : 271-280 |
| [2] | Yee T F, Grossmann I E . Simultaneous optimization models for heat integration-Ⅱ. Heat exchanger network synthesis[J]. Computers & Chemical Engineering , 1990, 14 (10) : 1165-1184 |
| [3] | Furman K. C, Sahinidis N V . Computational complexity of heat exchanger network synthesis[J]. Computers & Chemical Engineering , 2001, 25 (9-10) : 1371-1390 |
| [4] | Grossmann I E . Review of nonlinear mixed-integer and disjunctive programming techniques[J]. Optimization and Engineering , 2002, 3 (3) : 227-252 DOI:10.1023/A:1021039126272 |
| [5] | FANG Da-jun(方大俊), CUI Guo-min(崔国民), XU Hai-zhu(许海珠) . Optimization of heat exchanger networks with cooperation differential evolution algorithm based on the penalty factors(基于罚因子协进化微分算法优化换热网络)[J]. J Chem Eng of Chinese Univ(高校化学工程学报) , 2015, 29 (2) : 407-412 |
| [6] | Gosselin L, Tye-Gingra M, Mathieu-Potvin F . Review of utilization of genetic algorithms in heat transfer problems[J]. International Journal of Heat and Mass Transfer , 2009, 52 (9-10) : 2169-2188 DOI:10.1016/j.ijheatmasstransfer.2008.11.015 |
| [7] | Siarry P, Michalewicz Z . Advances in metaheuristics for hard optimization[M]. Berlin: Springer Heidelberg, 2008 : 293 -315. |
| [8] | Danish M, Kumar S, Qamareen A . Optimal solution of MINLP problems using modified genetic algorithm[J]. Chemical Product and Process Modeling , 2006, 1 (1) : 1934-2659 |
| [9] | Young C T, Zheng Y, Yeh C W . Information-guided genetic algorithm approach to the solution of MINLP problems[J]. Ind Eng Chem Res , 2007, 46 (5) : 1527-1537 DOI:10.1021/ie060727h |
| [10] | KANG Li-xia(康丽霞), ZHANG Yan-rong(张燕蓉), TANG Ya-zhe(唐亚哲) . Paralleled SQP algorithm for solution of MINLP problems based on GPU acceleration(基于GPU加速求解MINLP问题的SQP并行算法)[J]. CIESC J(化工学报) , 2012, 63 (11) : 3597-3601 |
| [11] | Wang L P, Chen K, Ong Y S . Advances in natural computation[M]. Berlin: Springer-Verlag, 2005 : 1051 -1059. |
| [12] | Gen M, Green D, Katai O . Intelligent and evolutionary systems[M]. Berlin: Springer Heidelberg, 2009 : 197 -216. |
| [13] | Wong M L. Parallel multi-objective evolutionary algorithms on graphics processing units[C]. Moutreal Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference, Motreal, 2009:2515-2522. |
| [14] | Munawar A, Wahib M, Munetomo M, et al. Advanced genetic algorithm to solve minlp problems over GPU[C]. New Orleans IEEE Congress on Evolutionarg Computation, New Orleans, 2011:318-325. |
| [15] | Tsutsui S, Collet P . Massively parallel evolutionary computation on GPGPUs[M]. Berlin: Springer Heidelberg, 2013 : 83 -104. |
| [16] | Zamora J M, Grossmann I E . A global MINLP optimization algorithm for the synthesis of heat exchanger networks with no stream splits[J]. Computers & Chemical Engineering , 1998, 22 (3) : 367-384 |
| [17] | Ciric A R, Floudas C A . Heat exchanger network synthesis without decomposition[J]. Computers & Chemical Engineering , 1991, 15 (6) : 385-396 |
| [18] | Pariyani A, Gupta A, Ghosh P . Design of heat exchanger networks using randomized algorithm[J]. Computers & Chemical Engineering , 2006, 30 (6-7) : 1046-1053 |
| [19] | Yerramsetty K M, Murty C V S . Synthesis of cost-optimal heat exchanger networks using differential evolution[J]. Computers & Chemical Engineering , 2008, 32 (8) : 1861-1876 |
| [20] | Vidyashankar K, Narasimhan S . Comparison of heat exchanger network synthesis using floudas and yee superstructures[J]. Indian Chemical Engineer , 2010, 52 (1) : 1-22 DOI:10.1080/00194501003759605 |




