机动输油管线是野战条件下输送油料的装配式管线系统,采用地面裸管铺设。输油任务完成之后,须排空管线中存油,撤收管线及装备,以备下次再用。采用空压机在管线一端充入压缩空气将管线中存油顶出管线的方法称为气顶油排空。进行气顶排空时管内存在气液两相流动。气液两相流存在随时间移动和变形的相界面,以及由相间相对运动引起的各种尺度的紊流涡团,伴随着复杂的质量和能量传递,其流动规律与单相流动完全不同,而且气液两相间的相互作用会导致油品中烃质成分的挥发、管内压力和流量的波动[1],使得排空过程系统参数变化表现出一定的随机性。
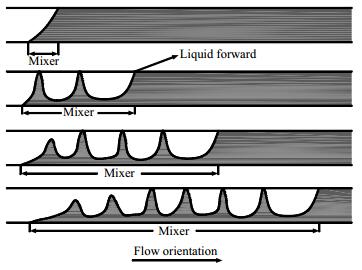
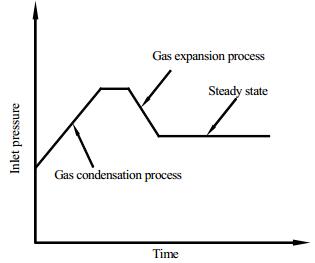
对于水平管路排空过程,管路气液混合段 (gas-oil mixer) 的发展过程如图 1所示,该段流型由单一分层流向段塞-分层流、环雾状流转变。随着排空进行,混合段长度不断增大。排空初始阶段,分层流液层厚度逐渐减小,之后分层流向段塞流转变,液体大部分被排出后,最终变为环雾状流[2]。由于气液两相流型同气液表观流速密切相关[3~5],而气顶排空过程气液流速不断变化,故该过程难以用简单的数学模型描述,计算难度很大。相应入口压力变化趋势如图 2所示,开始管内液体较多,气体速度较小,混合段之前的气体被压缩 (gas condensation),压力增大。随着液体不断被排出,气体速度高于液体速度,气体开始膨胀 (gas expansion),压力减小。最后液体大部分被排出,管内为气体单相流动,压力达到稳定 (steady state)。
|
图 1 气顶排空管路流动状态示意图 Fig.1 Schematic diagram of flow status in gas-cap emptying |
|
图 2 入口端压力示意图 Fig.2 Pressure variation at the inlet |
目前,管道气液两相流问题主要存在于海底油气混输管道、核电换热设备、地面管道试运行时空管投油等工程背景中[6~8]。对于野战管线气顶排空这一特殊工况的研究较少,但其本质依然是气液两相流动问题,可以借鉴当前主流的气液两相流数值模拟方法进行研究。S. F. ALI等[9]利用OLGA软件对大管径水平-垂直上升管两相流动进行了数值模拟,预测上升管底部的压力和流型,仿真值与实验值吻合良好。Mehdi Davoudi等[10]利用OLGA对南阿曼湾输气管道清管过程进行模拟,将甘醇含量、清管器运行时间以及液塞体积的仿真值同现场数据进行比较,得到在600和300 MMSCFD输量下仿真清管时间与真实值之间分别相差0.7和1.3 h。覃柏英等[11]采用加权三阶ENN格式离散Euler方程、LS运输方程及其重新初始化方程的空间导数,耦合三阶Runge-Kutta法离散它们的时间导数,探讨了气液两相流问题的高精度数值模拟。马晓旭等[12]利用多场耦合有限元软件ADINA,结合任意拉格朗日-欧拉 (ALE) 动网格方法,对水平弯管内气液两相流诱导振动问题进行了数值模拟研究,重点考察了管结构振动响应特性及流型、体积含气率β和分相折算速度等对激振力的影响。
目前OLGA、PROFES、TACITE等瞬态多相流模拟软件广泛应用于石油与天然气工业中,但鲜有这些软件模拟气顶排空过程的报道。OLGA 6.0全动态仿真软件可以模拟绝热、传热、瞬态条件下的气液两相流动。该软件在管路系统所有位置和不同的时间步长内计算流量、压力和温度,每个时步内计算水力和热力平衡方程。软件通过用户自定义状态方程计算气液状态参数。软件计算温度时充分考虑了管线、容器以及周边环境的热力特点。本文利用OLGA6.0多相流模拟软件对气顶排空过程中压力、流量、持液率等参数的变化规律进行研究,将结果与现场实验测试结果进行对比验证,探求利用OLGA进行气顶排空过程模拟的可能性。
2 数学模型和计算方法 2.1 扩展的双流体模型依据上述分析,对比多种两相流计算模型,选用较适合排空实际的双流体模型。双流体模型将两相流体单独处理,认为两相均为连续介质,把两相的界面看作一个移动的边界,它们的运动规律遵守各自的控制方程,但存在相间的相互作用[13]。两种流体在时空上共存,这既可理解为在一个有限空间单元中,两种流体各占据一部分体积,也可理解为在一个空间位置上两种流体各以一定的概率出现。气体、液层、液滴分别采用独立的质量守恒方程,如式 (1)~(3) 所示。
气相:
| $ \frac{\partial }{{\partial t}}\left( {{V_{\rm{g}}}{\rho _{\rm{g}}}} \right) = - \frac{1}{A}\frac{\partial }{{\partial t}}\left( {A{V_{\rm{g}}}{\rho _{\rm{g}}}} \right) + {\psi _{\rm{g}}} + {G_{\rm{g}}} $ | (1) |
壁面液层:
| $\frac{\partial }{{\partial t}}\left( {{V_{\rm{L}}}{\rho _{\rm{L}}}} \right) = - \frac{1}{A}\frac{\partial }{{\partial z}}\left( {A{V_{\rm{L}}}{\rho _{\rm{L}}}{v_{\rm{L}}}} \right) - {\psi _{\rm{g}}}\frac{{{V_{\rm{L}}}}}{{{V_{\rm{L}}} + {V_{\rm{D}}}}} - {\psi _{\rm{e}}} + {\psi _{\rm{D}}} + {G_{\rm{L}}}$ | (2) |
液滴:
| $ \frac{\partial }{{\partial t}}\left( {{V_{\rm{L}}}{\rho _{\rm{L}}}} \right) = - \frac{1}{A}\frac{\partial }{{\partial z}}\left( {A{V_{\rm{D}}}{\rho _{\rm{L}}}{v_{\rm{D}}}} \right) - {\psi _{\rm{g}}}\frac{{{V_{\rm{L}}}}}{{{V_{\rm{L}}} + {V_{\rm{D}}}}} - {\psi _{\rm{e}}} + {\psi _{\rm{D}}} + {G_{\rm{D}}} $ | (3) |
式中Vg,VL和Vd分别表示气体、液层、液滴的体积分数,v是速度。A是管子截面积,Ψg表示相间传质速率,Ψe和ΨD分别表示气体夹带和沉积速率。F相的质量源表示为Gf。下标g, L, D, I表示气相、液层、液滴、界面。
方程 (1)~(3) 可以扩展成关于压力、温度和相含率的方程,假设密度可由式 (4) 得出:
| ${\rho _{\rm{f}}} = \rho (p,T,{R_{\rm{s}}})$ | (4) |
式中Rs是气体质量分数。
动量守恒方程表示为式 (5)~(7)。
气相:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}({V_{\rm{g}}}{\rho _{\rm{g}}}{v_{\rm{g}}}) = - {V_{\rm{g}}}(\frac{{\partial p}}{{\partial z}}) - \frac{1}{A}\frac{\partial }{{\partial z}}(A{V_{\rm{g}}}\rho {}_{\rm{g}}{v_{\rm{g}}}^2) - {\lambda _{\rm{g}}}\frac{1}{2}{\rho _{\rm{g}}}\left| {{v_{\rm{g}}}} \right|{v_{\rm{g}}} \times \frac{{{S_{\rm{g}}}}}{{4A}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ + }}{\lambda _i}\frac{1}{2}{\rho _{\rm{g}}}\left| {{v_{\rm{r}}}} \right|{v_{\rm{r}}}\frac{{{S_i}}}{{4A}} + {V_{\rm{g}}}{\rho _{\rm{g}}}g\cos \alpha + {\psi _{\rm{g}}}{v_{\rm{a}}} - {F_{\rm{D}}} \end{array} $ | (5) |
液滴:
| $\begin{array}{l} \frac{\partial }{{\partial t}}({V_{\rm{D}}}{\rho _{\rm{L}}}{v_{\rm{D}}}) = - {V_{\rm{L}}}(\frac{{\partial p}}{{\partial z}}) - \frac{1}{A}\frac{\partial }{{\partial z}}(A{V_{\rm{D}}}{\rho _{\rm{L}}}v_{\rm{D}}^2) + {V_{\rm{D}}}{\rho _{\rm{L}}}g\cos \alpha \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {\psi _{\rm{g}}}\frac{{{V_{\rm{D}}}}}{{{V_{\rm{L}}} + {V_{\rm{D}}}}}{v_{\rm{a}}} + {\psi _{\rm{e}}}{v_i} - {\psi _{\rm{d}}}{v_{\rm{D}}} + {F_{\rm{D}}} \end{array}$ | (6) |
壁面液层:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}({V_{\rm{L}}}{\rho _{\rm{L}}}{v_{\rm{L}}}) = \\ - {V_{\rm{L}}}(\frac{\partial }{{\partial z}}) - \frac{1}{A}\frac{\partial }{\partial }(A{V_{\rm{L}}}{\rho _{\rm{L}}}v_{\rm{L}}^{^2}) - {\lambda _{\rm{L}}}\frac{1}{2}{\rho _{\rm{L}}}\left| {{v_{\rm{L}}}} \right|{v_{\rm{L}}}\frac{{{S_{\rm{L}}}}}{{4A}} + {\lambda _i}{\rho _{\rm{g}}}\frac{1}{2}\left| {{v_{\rm{r}}}} \right|{v_{\rm{r}}}\frac{{{S_i}}}{{4A}}\\ + {V_{\rm{L}}}{\rho _{\rm{L}}}g\cos \alpha - {\psi _{\rm{g}}}\frac{{{V_{\rm{L}}}}}{{{V_{\rm{L}}} + {V_{\rm{D}}}}}{v_{\rm{a}}} - {\psi _{\rm{e}}}{v_i} + {\psi _{\rm{d}}}{v_{\rm{d}}} - {V_{\rm{L}}}d({\rho _{\rm{L}}} - {\rho _{\rm{g}}})g\frac{{\partial {V_{\rm{L}}}}}{{\partial z}}\sin \alpha \end{array} $ | (7) |
又因为,
| ${V_{\rm{g}}} + {V_{\rm{L}}} + {V_{\rm{D}}} = 1$ | (8) |
联立质量、动量守恒方程和式 (8)
得到单一方程求解压力和相流量:
| $\begin{array}{l} [\frac{{{V_{\rm{g}}}}}{{{\rho _{\rm{g}}}}}{(\frac{{\partial {\rho _{\rm{g}}}}}{{\partial p}})_{T,{R_{\rm{s}}}}} + \frac{{1 - {V_{\rm{g}}}}}{{{\rho _{\rm{L}}}}}{(\frac{{\partial {\rho _{\rm{L}}}}}{{\partial p}})_{T,{R_{\rm{s}}}}}]\frac{{\partial p}}{{\partial t}} = \\ - \frac{1}{{A{\rho _{\rm{g}}}}}\frac{{\partial (A{V_{\rm{g}}}{\rho _{\rm{g}}}{v_{\rm{g}}})}}{{\partial z}} - \frac{1}{{A{\rho _L}}}\frac{{\partial (A{V_{\rm{L}}}{\rho _{\rm{L}}}{v_{\rm{L}}})}}{{\partial z}} - \frac{1}{{A{\rho _{\rm{L}}}}}\frac{{\partial (A{V_{\rm{D}}}{\rho _{\rm{L}}}{v_{\rm{D}}})}}{{\partial z}}\\ + {\psi _{\rm{g}}}(\frac{1}{{{\rho _{\rm{g}}}}} - \frac{1}{{{\rho _{\rm{L}}}}}) + {G_{\rm{g}}}\frac{1}{{{\rho _{\rm{g}}}}} + {G_{\rm{L}}}\frac{1}{{{\rho _{\rm{L}}}}} + {G_D}\frac{1}{{{\rho _{\rm{L}}}}} \end{array}$ | (9) |
气顶排空过程为动态、多段耦合的流动过程,随着排气过程的进行,气液混合段分别为分层流、分层-段塞流、环雾流。OLGA双流体模型中的摩阻系数与界面湿周和流型有关。模型考虑了两种最基本的流型:以泡状流、段塞流为代表的间歇流和以分层流、环雾流为代表的分离流。OLGA采用统一模型,不需要用户单独指定持液率计算公式,因此对于每一个管段,OLGA可以动态预测流型并得到基于流型的流动参数。
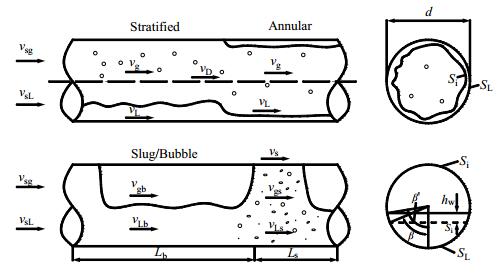
2.2.1 分离流如图 3所示,分层流 (Stratified) 和环雾流 (Annular-mist) 的特点是气液两相单独流动,稳定地被分为两个部分。所以下述滑移公式 (10) 中的气液滑移速率RD为1。
|
图 3 分层环雾状流和段塞流示意图 Fig.3 Schematic diagram of stratified annular mist and slug |
| ${{v}_{\text{g}}}={{R}_{\text{D}}}({{v}_{\text{L}}}+{{v}_{\text{r}}})$ | (10) |
分层流产生波动时转换为波状流,平均波浪高度hw可由下式求得:
| ${{h}_{w}}=\frac{1}{2}\left\{ \frac{{{\rho }_{\text{g}}}{{({{v}_{\text{g}}}-{{v}_{\text{L}}})}^{2}}}{2({{\rho }_{\text{L}}}-{{\rho }_{\text{g}}})g\sin \alpha }+\sqrt{{{\left[ \frac{{{\rho }_{\text{g}}}{{({{v}_{\text{g}}}-{{v}_{\text{L}}})}^{2}}}{2({{\rho }_{\text{L}}}-{{\rho }_{\text{g}}})g\sin \alpha } \right]}^{2}}-\frac{4\sigma }{({{\rho }_{\text{L}}}-{{\rho }_{\text{g}}})g\sin \alpha }} \right\}$ | (11) |
当波浪高度达到管道的顶端或
在气泡流和段塞流工况下,平均气相速率满足下述公式:
| ${{v}_{\text{g}}}=\frac{1-{{V}_{\text{g}}}}{(1/{{C}_{0}}-{{V}_{\text{g}}})}\left[ {{v}_{\text{L}}}+\frac{{{v}_{\text{0b}}}}{{{C}_{0}}(1-{{V}_{\text{g}}})} \right]$ | (12) |
对于充分发展的液塞较长的段塞流 (≥ 10D),任意倾角下段塞 (气泡) 速度vb可由如下关系式近似得到:
| $ {{v}_{\text{b}}}={{C}_{0}}({{v}_{\text{sL}}}+{{v}_{\text{sg}}})+{{v}_{\text{0b}}} $ | (13) |
其中
| $ {{C}_{0}}=\left\{ \begin{align} & 1.05+0.15{{\cos }^{2}}\alpha \ \ \text{for }{{N}_{\text{Fr}}}<3.5 \\ & 1.20\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\ }_{\ \ }}{{_{\ }}_{\ }}\text{for }{{N}_{\text{Fr}}}>3.5 \\ \end{align} \right. $ | (14) |
| ${{v}_{\text{0b}}}=\left\{ \begin{align} & {{v}_{\text{0V}}}\cos \alpha +{{v}_{\text{0H}}}\sin \alpha \ \ \text{for}\ \ {{N}_{\text{Fr}}}<3.5 \\ & {{v}_{\text{0V}}}\cos \alpha \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{for}\ {{N}_{\text{Fr}}}>3.5 \\ \end{align} \right.$ | (15) |
其中v0V和v0H分别为垂直和水平管内静止液层中气泡的速度。
在间歇流中,当气体全部被液塞夹带时将产生连续气泡流,此时液塞中的含气率Vgs大于管流的平均含气率Vg。
3 数值模拟条件本文采用文献[14]现场实验数据对气顶排空数值模拟进行验证。仿真管路系统流程如图 4所示
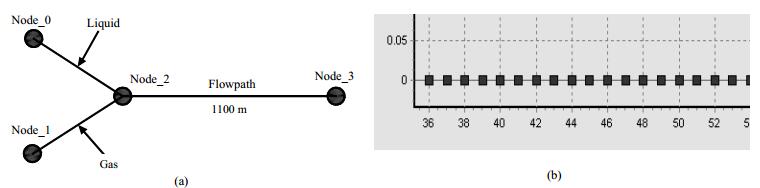
实验和仿真均采用DN100机动管线,管长1100 m,水平地面铺设,空压机位于管路始端,末端为大气。管路入口和出口分别布置气体流量计和液体流量计,沿线布置2个测试点,每个测试点包含双探针电容传感器和压力变送器,两个测试点距离入口分别为126和906 m。通过控制闸阀开度来改变排空初始入口压力,排空介质为水,管路出口压力为大气压。实验受场地限制,管路呈蛇形布置,存在弯头和连接器,仿真管路为水平直管,仿真路由图见图 4(a),节点长度为1 m,节点划分局部细节见图 4(b)。表 1为管路特性。
|
图 4 仿真流程图和节点划分 Fig.4 Simulation flowchart (a) and node definition (b) |
| 表 1 管路特性 Table 1 The main parameters of the pipeline |
仿真通过PVTsim软件生成流体物性参数,气体为理想气体,液体为水。由于实验在较低压力下进行,认为流体与环境之间不存在传热传质。由于管路入口处压力不断变化 (图 2),实验改变闸阀开度可以控制初始入口压力,闸阀开度固定后入口质量流量不变,所以实验入口边界为定初始压力,仿真入口边界为定质量流量 (massflow),出口为定压力边界 (pressure)。仿真时间为535 s。经仿真计算,入口初始压力与质量流量对应关系见表 2所示。表 2为实验和仿真边界条件对应值。
| 表 2 边界条件 Table 2 Boundary conditions |
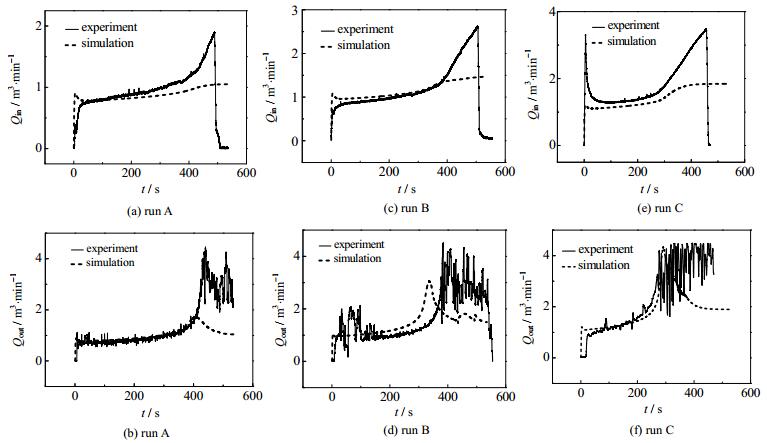
排空过程的瞬态特性决定了管道各点的流量具有瞬变性,探讨管道入口处 (Qin) 和出口处 (Qout) 流量的变化趋势,可以从总体上判断气液两相的流量变化规律。排空初期管道入口处为气体,出口处为液体,但是随着排空的进行,气液混合段在管道中运动且不断伸长,一定时间后,管道出口出现气液混合物,并持续一段时间,用涡轮流量计采集混合物流量,仿真检测参数选择液体流量。
图 5为三种工况下 (A、B、C) 管道入口和出口流量随时间变化的结果示意图。由图 5(a)、(c)、(e) 可以看出,仿真计算的入口流量变化趋势与测量值基本一致。即增长过程分为三个阶段,排空初始阶段入口液体由静止变为流动,流量迅速增长;排空中间阶段流量缓慢增长;排空结尾阶段液体大部分被排出,流量再次迅速增长。仿真值与实验值在350 s之前 (初始段和稳定段) 曲线形状吻合较好,350 s之后 (结尾段) 差别较大。仿真值小于实验值,原因是实验过程气体压缩性体现较明显,排空结尾段液体大部分被排出,气体由排空过程的压缩状态到自由流动存在流量的跃变,而仿真未考虑液体排空瞬间气体由压缩状态向无压流的跃变过程,所以仿真值和实验测量值存在一定差异。
|
图 5 流量变化 Fig.5 Results of flowrate variation |
由图 5(b)、(d)、和 (f) 可得,不同于入口流量,出口流量经历四个阶段。前三阶段与入口相同,即迅速上升,缓慢上升,迅速上升。但排空末尾出口流量会出现下降的现象,且下降过程波动剧烈。仿真与实验得到的流量变化趋势在前三阶段基本一致,但是排空结尾段仿真值明显小于实验值,且波动幅度较小。原因是排空结尾出口为气液混合物,呈塞状流流出管道,实验所采用的涡轮流量计测量的是气液混合物的流量,而OLGA软件中测量的是液体流量,且仿真得到出口流型为层状流,所以流量波动较小。
工况A和B流量下降时间的计算值略小于实验值,工况C基本吻合。原因是前两种工况仿真过程液体前锋到达出口时间更短,即排空速度更快。此差别可归因于仿真过程将管路设置为直管,而实验中管路存在弯头和连接器,局部摩阻较大,排空速度较小。
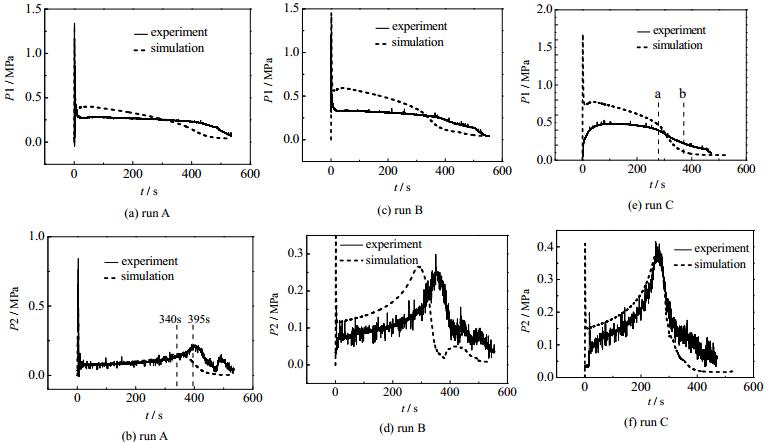
4.2 压力变化特性将两个测试点的压力进行对比分析,P1为第一测压点处的压力,P2为第二测压点的压力。图 6为压力随时间变化趋势。
|
图 6 压力变化 Fig.6 Results of pressure variation |
由图 6(a~f)可以看出,仿真和实验值具有相同的变化趋势,1号测压点压力呈现缓慢下降的趋势,6号点压力变化规律为先增加后下降。初始入口压力越大,变化幅度越明显。
分析图 6(a)、(c)和 (e) 可得管路初始端的压力变化,液体前锋到达1号测压点时间较短,此点在整个排空过程中以气体为主。气体的压力主要由气体的压缩性决定,排空初始阶段管内液体较多,空压机提供压力较小,入口处处于“憋压”状态。随着排空进行,液体逐渐减少,气体由压缩状态变为膨胀状态,所以压力逐渐减小。当液体前锋到达出口时,压力出现剧烈下降阶段,此过程在工况C中尤为明显,如图 6(e)中a-b段所示,压力突降是伴随着入口流量的徒增而发生的,这两个过程均发生在300~400 s。液体前锋到达出口之前仿真值大于实验值,之后小于实验值,且入口压力越大,误差越大。由此可见排空过程中,入口处到1号测压点压降的仿真值小于实验值,排空结尾大于实验值。这是因为排空进行过程中,气液混合物之间相互作用消耗了一部分压能,但仿真计算中未体现这一过程,所以P1小于仿真值;排空结尾,仿真计算结果为液体全部排空,见图 6(c)和(e),所以P1降为大气压,而实验结果为管内存在气液混合物,所以此时P1大于仿真值。
由图 6(b)、(d)和 (f) 可得,2号测压点压力的实验值和仿真值变化趋势相同,呈单峰形式,即先增大后减小。
由图 6(b)可得,仿真所得压力峰值比实验小,波峰到达时间不同,仿真为t = 340 s,而实验为t = 395 s。340 s之前仿真与实验值吻合较好,但是340 s之后仿真值低于实验值。波峰时间不同的原因是仿真排空时间较短,液体前锋到达测压点的时间相应较短;吻合度不同的原因是,340 s之前,出口流体流速的仿真值大于实验值,之后小于实验值,所以造成压降在340s之前仿真值较大而后仿真值较小。实验压力到达峰值后又出现了小幅波动,这同样可归因于实验排空末尾管路存在气液混合物。
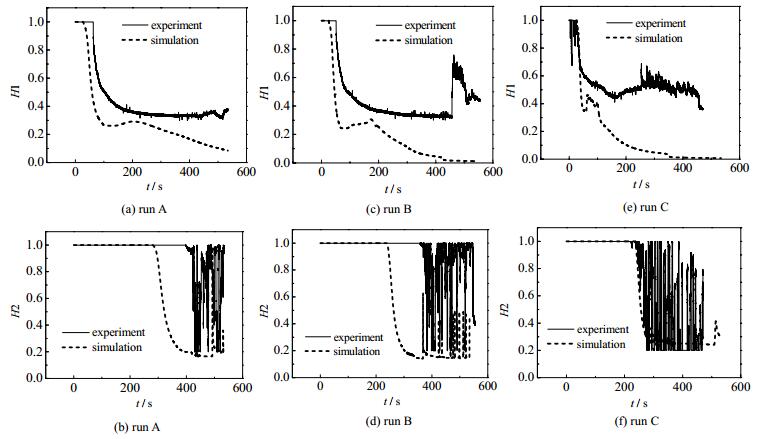
4.3 持液率变化图 7为三种工况下测试点1(H1) 和2(H2) 的持液率变化。
|
图 7 持液率变化 Fig.7 Results of liquid holdup variation |
由图 7(a)、(c)和 (e) 可以看出,三种工况下实验排空情况不理想,测试点1的最终持液率均在0.4以上,说明管内有将近一半的液体未排出,且初始压力越大,分层流更易向段塞流转变。而仿真值更接近真实情况,持液率在经历了短暂的波动后最终都会降为0。这种情况可能由多种因素导致。首先,实验管路为蛇形布置的机动管线,弯头和连接器的存在会使管路局部摩阻升高,从而降低排空效率;其次双探针式持液率传感器在静态测量时精度较高,动态测量精度有待考量。由图 7(a~f)可以看出,工况C液体前锋到达时间的仿真和实验值吻合度最高,而工况A、B仿真值小于实验值。说明初始压力越高,排空时间的仿真值和实验值越接近。
对比图 7(b)、(d)和 (e) 还可以得到,工况C液体前锋到达2号测试点的时间最短,即初始排气压力越高,排空速度越快。实验所得气液混合段以段塞流 (slug flow) 为主,仿真以塞状流 (plug flow) 为主,且初始排气压力越大,越不容易形成液塞,因为排气压力越大气液两相流速越大,形成段塞的几率越小[15]。由图 7(b)和(d)可得,仿真所得段塞频率远低于实验值。原因可以解释为仿真气液流速小于实验值,而OLGA流型判断机理是根据经验流型图所得,与实验工况略有差别。
5 结论利用OLGA6.0对机动管线气顶排空过程进行数值模拟,并利用文献[14]实验数据进行验证。结论如下:
(1) 数值模拟结果与实验测试结果吻合较好,入口压力越大,仿真与实验的排空时间越接近。实验中机动管线具有连接器、弯头等特殊的管路结构;探针式持液率传感器、涡轮流量计的测量精度有待提高;数值模拟对摩阻项的处理不够精确;OLGA持液率判据与本文所列工况有差别。以上这些原因都可导致数值模拟与实验之间的误差。
(2) 通过与实验的对比,OLGA仿真模型及计算方法具有一定的合理性、适用性和科学性,在动辄数百公里的机动管线排空问题的研究中,由于实验受到地形限制难以开展,可采用仿真的方法进行研究。
符号说明:
A —截面积,m2
d —直径,m
G —质量源
H —持液率
h —高度,m
P —压力,Pa
Q —流量,m3·min-1
Rs —气体质量分数
S —湿周,m
t —时间,s
VD —液滴体积分数
Vg —气体体积分数
VL —液层体积分数
v —速度,m·s-1
α —管路倾角,radian
λ —摩阻系数
ρ —密度,kg·m-3
Ψg —相间传质速率
Ψe —气体夹带速率
ΨD —气体沉积速率
| [1] | HUANG Na(黄娜), ZHOU Yun-long(周云龙), GAO Ju(高聚). Numerical study of high pressure vapor-liquid flow in large-diameter vertical pipes(大管径垂直管道内高压汽液混合流动的数值研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2015, 29(6): 1348-1355. |
| [2] | JIANG Jun-ze(姜俊泽), ZHANG Wei-ming(张伟明), LI Zheng-yang(李正阳). Mathematic simulation on gas-liquid two-phase flow of pipe pigging by gas condition(管道充气排液工况下气液两相流数值模拟研究)[J]. Journal of System Simulation(系统仿真学报) , 2013, 25(2): 383-388. |
| [3] | Bhagwat S M, Ghajar A J. A flow pattern independent drift flux model based void fraction correlation for a wide range of gas-liquid two phase flow[J]. International Journal of Multiphase Flow , 2014, 59(2): 186-205. |
| [4] | Ruspini L C, Marcel C P, Clausse A. Two-phase flow instabilities:a review[J]. International Journal of Heat & Mass Transfer , 2014, 71(3): 521-548. |
| [5] | Talley J D, Worosz T, Kim S, et al. Characterization of horizontal air-water two-phase flow in a round pipe part Ⅰ:flow visualization[J]. International Journal of Multiphase Flow , 2015, 76: 212-222. DOI:10.1016/j.ijmultiphaseflow.2015.06.011. |
| [6] | WANG Li-man(王立满), HE Li-min(何利民), WANG Yu-zhu(王玉柱), et al. Simulation of by-pass pigging in the NGL pipeline(天然气凝析液管道射流清管模拟)[J]. Pipeline Technique & Equipment(管道技术与设备) , 2015(2): 60-63. |
| [7] | Ansari M R, Azadi R. Effect of diameter and axial location on upward gas-liquid two-phase flow patterns in intermediate-scale vertical tubes[J]. Annals of Nuclear Energy , 2016, 94: 530-540. DOI:10.1016/j.anucene.2016.04.020. |
| [8] | DENG Tao(邓涛), GONG Jing(宫敬), YU Da(于达), et al. Influence of complex terrain on the pressure test and drainage of long-distance gas pipeline(复杂地形对长距离输气管道试压排水的影响)[J]. Oil & Gas Storage and Transportation(油气储运) , 2014(12): 1326-1330. |
| [9] | AliS F, Yeung H. Experimental investigation and numerical simulation of two-phase flow in a large-diameter horizontal flow line vertical riser[J]. Petroleum Science & Technology , 2010, 28(11): 1079-1095. |
| [10] | Davoudi M, Heidari Y, Mansoori S A A. Field experience and evaluation of the South Pars sea line pigging, based on dynamic simulations[J]. Journal of Natural Gas Science & Engineering , 2014, 18: 210-218. |
| [11] | QIN Bo-ying(覃柏英), LIN Xian-kun(林贤坤), RONG Ji-li(荣吉利), et al. High precision numerical simulation for gas liquid two phase flow(气液两相流问题的高精度数值模拟)[J]. Journal of Vibration & Shock(振动与冲击) , 2016, 35(9): 79-85. |
| [12] | MA Xiao-xu(马晓旭), TIAN Mao-cheng(田茂诚), ZHANG Guan-min(张冠敏), et al. Numerical investigation on gas liquid two phase flow induced vibration in a horizontal tube(水平管内气液两相流诱导振动的数值研究)[J]. Journal of Vibration & Shock(振动与冲击) , 2016, 35(16): 204-210. |
| [13] | Ishii M, Hibiki T. Thermo-fluid dynamic theory of two-phase flow[M].New York: Springer, 2016. |
| [14] | JIANG Jun-ze (姜俊泽). Experiment study on mobile pipeline emptying characteristics and mechanism of gas-liquid mixture formation (机动管线排空特性与气液混合物形成机理实验研究) [D]. Chongqing (重庆): Logistical Engineering University (后勤工程学院), 2012. |
| [15] | Al-Safran E, Sarica C, Zhang H Q, et al. Investigation of slug flow characteristics in the valley of a hilly-terrain pipeline[J]. International Journal of Multiphase Flow , 2005, 31(3): 337-357. DOI:10.1016/j.ijmultiphaseflow.2004.11.002. |




