2. 西安交通大学 能源与动力学院, 陕西 西安 710049
2. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
原油脱水(盐)是石油工业必不可少的预处理工序,主要包括化学法、过滤法、重力沉降法、离心分离法、超声波法、热处理法和电聚结法等[1~4]。其中,电聚结是重要的原油脱水技术,主要依靠水滴间偶极吸引力促进聚并,加速水滴沉降[5]。液滴聚并和电场条件、液滴物性及空间位置等有关。王贞涛等[6]用VOF方法和漏电介质模型模拟了静电场中液滴变形和内部流动。Mohammadi [7]研究了油中液滴在电场作用下的聚并,发现液滴连线与电场线夹角越小,聚结越快。然而,液滴在电场中行为复杂,除了液滴聚并外,还需考虑破碎、迁移和聚并产生的二次液滴等。任瑞娟等[8]研究了不同波形电场下液滴极化变形规律,发现存在使变形度最大的最佳频率。与均匀电场相比,通常认为非均匀电场更为高效。Mhatre等[9]对针-板电极中的液滴群行为展开了研究。陈庆国等[10]研究了非均匀电场中液滴变形和聚并,发现增大非均匀系数能提高液滴聚结速率。陈庆国等[11]采用流场和电场耦合的方法研究了交流电场下的液滴变形,并分析了液滴直径对液滴聚并速率的影响。陈庆国等[12]又通过相场方法研究均匀电场和非均匀电场下液滴的运动特性,发现非均匀电场下的液滴接触机率更大。从以上研究发现,以往对均匀电场的研究较充分,但是对于非均匀电场的研究较匮乏。与均匀电场相比,非均匀电场中,W/O乳状液中的水滴受介电泳力向高场强区域迁移、聚集,从而提高了水滴的聚结效果[13]。基于此,课题组提出一种应用于电脱水(盐)罐中、能产生非均匀电场的蜂窝-悬针电极[14],并以此为基础,简化得到同轴六边形-圆电极的数值模型,在施加正弦交流电场的条件下,对电极中液滴受介电泳力的迁移运动规律展开探究,分析电场参数和物性参数的影响,为高效紧凑电聚结设备的研发及应用提供理论依据。
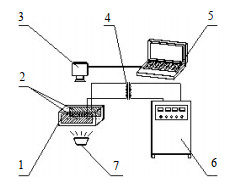
2 实验装置与材料实验装置及流程如图 1所示,包括高频脉冲电源、数码显微镜、观测单元等。
|
图 1 实验装置及流程 Fig.1 Schematic diagram of the experimental set-up 1. electrocoalescence cell 2. electrodes 3. microscope 4. transformer 5. computer 6. power supply 7. light source |
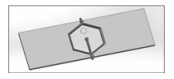
高频脉冲电源由中国石油大学(华东)自行研制,电压调节范围:0~9.8 kV,频率调节范围:0.41~6.3 kHz,脉宽比调节范围:0.1~0.875。采用江西凤凰光学仪器集团生产的PH50数码显微镜,拍摄得到的图像经ImageJ软件处理。如图 2所示,实验观测单元和数值模型一致,且液滴的运动和观测区域已在图中用圆圈标出。
|
图 2 观测单元 Fig.2 Schematic diagram of the experimental cell for observation |
实验中,用微量计量器向蓖麻油中注射一定体积的去离子水,形成一定尺寸的水滴。其中,蓖麻油和去离子水物性如表 1所示。
|
|
表 1 实验材料物性 Table 1 Properties of experimental materials |
此外,蓖麻油和去离子水的界面张力为32.20 mN·m-1。
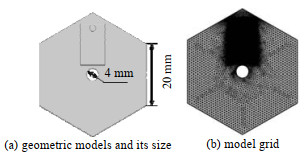
3 模拟方法 3.1 几何模型及边界条件本研究在COMSOL Multiphysics中建立如图 3(a)所示的二维模型,其模型网格划分如图 3(b)所示。为了计算的高效和准确,对液滴运动区域进行了网格细化。
|
图 3 几何模型和网格划分 Fig.3 Geometric models and grid partitioning |
由表 2可知,油水两相的Clausius-Mossotti系数为0.92,表明液滴向高场强区域运动[15]。此外,为了验证模拟结果的准确性,开展显微实验,并将模拟结果与实验结果进行对比。
|
|
表 2 数值模拟中物性参数 Table 2 Properties of materials used in simulation |
相场模型通过相场变量ϕ来得到两相界面的信息,实现对界面的追踪,把表面张力等效为场变量梯度与化学势的乘积,并将其作为体积力的一项加入控制流体压力和速度的Navier-Stokes方程中:
| $ \rho \frac{\partial u}{\partial t} \nabla \cdot \mu\left[\nabla u+(\nabla \boldsymbol{u})^{\mathrm{T}}\right]+\rho(u \cdot \nabla) u+\nabla p=F $ | (1) |
式中:ρ为流体密度,kg·m-3;u为流体速度,m·s-1;t为时间,s;
相场模型通过4阶偏微分Cahn-Hilliard方程来控制相场变量的演化:
| $ \frac{\partial \phi}{\partial t}+u \cdot \nabla \phi=\nabla \cdot \gamma \nabla G $ | (2) |
式中:ϕ为相场变量;γ为迁移率,m3·s·kg-1;G为化学势,Pa。
3.3 电场和流场耦合计算区域内电场由Maxwell方程控制:
| $ -\nabla \cdot\left(\varepsilon_{0} \varepsilon_{\mathrm{r}} E\right)=0 $ | (3) |
式中:ε0为真空介电常数,F·m-1;εr为流体相对介电常数;E为电场强度,V·m-1。
电场产生电应力FE可由Maxwell应力张量T推导得到,由式(4)给出:
| $ F_{\mathrm{E}}=\nabla \cdot \boldsymbol{T}=\nabla \cdot\left[E \boldsymbol{D}^{\mathrm{T}}-\frac{1}{2}(E \cdot D) I\right] $ | (4) |
式中:D为电位移,C·m-2;DT为电位移的转移矩阵,C·m-2;I为电流,A。
3.4 液滴位置和速度的确定如图 4和5所示,本研究以液滴在运动方向上的最长截线的中点为液滴中心,并以液滴中心和电极中心的距离s表征液滴位置。
|
图 4 液滴中心确定图 Fig.4 Determination of droplet center |
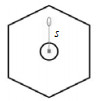
|
图 5 液滴位置确定图 Fig.5 Determination of droplet position |
模拟过程中,每隔0.005 s对解进行一次存储和导出,经后处理后可得到自模拟开始起0、0.005、0.01 s、······等时刻液滴位置的数据,进而得到液滴运动速度。
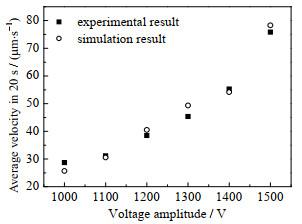
3.5 液滴位置和速度的确定由图 6可知,模拟和单液滴介电泳迁移实验(图 7)吻合良好。此外,进行了网格无关性验证,综合计算效率和结果准确性,确定网格密度为430.576 923 1个·mm-2。
|
图 6 实验和模拟结果对比 Fig.6 Comparison of experimental and simulation results about effects of electric field strength on dielectrophoresis velocity (AC electric field: frequency 50 Hz) |

|
图 7 单液滴介电泳迁移 Fig.7 Dieletrophoresis results of single droplet (AC electric field 1 000 V, 50 Hz; droplet diameter 1.041 mm) |
模拟得到的液滴在非均匀电场中受介电泳力迁移过程如图 8所示。
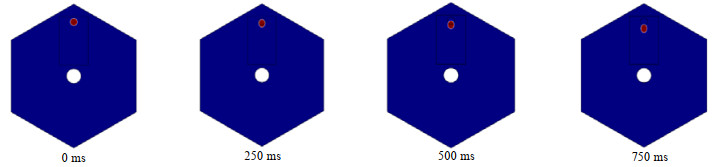
|
图 8 液滴在非均匀电场中的介电泳迁移 Fig.8 Profiles of droplet movement in non-uniform electric fields (potential difference amplitude 30 000 V; frequency 50 Hz; diameter 2.0 mm; viscosity 0.35 Pa·s) |
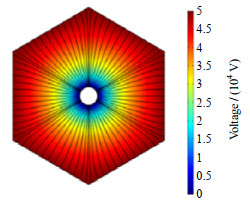
由图 8可知,非均匀电场中,液滴向着电极中心区域运动,受电场力作用拉伸变形。图 9给出了电场模拟图,由电场线稀疏可知,越靠近电极中心区域,场强越高。如图 10所示,液滴的迁移使原本分散的液滴聚集,缩短了彼此间距离[9]。
|
图 9 同轴六边形-圆电极电场模拟图 Fig.9 Simulative electric fields of coaxial hexagon-circle electrodes (different colors present different electric potentials) |
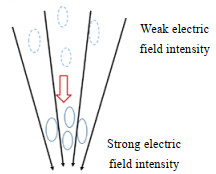
|
图 10 液滴在介电泳力作用的聚集 Fig.10 Gathering processes of droplets under dielectrophoresis forces |
在非均匀电场中,液滴受到的介电泳力FDEP表达式如下[16]:
| $ F_{\mathrm{DEP}}=2 {\rm{ \mathsf{ π}}} d^{3} \varepsilon_{\mathrm{m}} \operatorname{Re}\left[K\left(\varepsilon_{\mathrm{p}}^{*}, \varepsilon_{\mathrm{m}}^{*}\right)\right] \nabla|E|^{2} $ | (5) |
式中:d为液滴直径,m;εm为连续相介电常数,F·m-1;
| $ K\left(\varepsilon_{\mathrm{p}}^{*}, \varepsilon_{\mathrm{m}}^{*}\right)=\frac{\varepsilon_{\mathrm{p}}^{*}-\varepsilon_{\mathrm{m}}^{*}}{\varepsilon_{\mathrm{p}}^{*}+2 \varepsilon_{\mathrm{m}}^{*}} $ | (6) |
式中:
| $ \varepsilon^{*}=\varepsilon-\mathrm{i}(\sigma / \omega) $ | (7) |
式中:
| $ \operatorname{Re}\left[K\left(\varepsilon_{\mathrm{p}}^{*}, \varepsilon_{\mathrm{m}}^{*}\right)\right]=\frac{\varepsilon_{\mathrm{p}}-\varepsilon_{\mathrm{m}}}{\varepsilon_{\mathrm{p}}+2 \varepsilon_{\mathrm{m}}} $ | (8) |
式中:εp为分散相的介电常数,F·m-1。当
| $ u_{\mathrm{DEP}}=\frac{2 d^{2} \varepsilon_{\mathrm{m}}\left(\varepsilon_{\mathrm{p}}-\varepsilon_{\mathrm{m}}\right) \nabla|E|^{2}}{3 \mu\left(\varepsilon_{\mathrm{p}}+2 \varepsilon_{\mathrm{m}}\right)} $ | (9) |
式(9)给出了理想情况下液滴的介电泳力迁移速度,但实际情况更加复杂。模拟得到的液滴电场力分布如图 11所示。
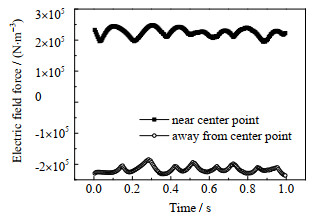
|
图 11 液滴两极电场力随时间变化趋势 Fig.11 Evolution of electric forces between two droplet poles |
液滴内部电荷受电场作用在液滴表面积累,电场作用于电荷而产生电场力。在垂直于电场方向上,电场力彼此对称、抵消;在平行于电场方向上,靠近电极中心端的电场力大于靠近边缘电极端的电场力,导致了液滴的介电泳迁移运动。由图 11可知,电场力随时间的变化呈近似正弦波形,这是液滴迁移致使所处位置变化导致,
4.2 电压幅值的影响正弦交流电场的电压幅值决定了电场强度。模拟计算中,液滴初始位置s=15 mm。
由图 12(a)可知,液滴瞬时速度随时间波动,速度波动幅度和频率随电压幅值的增大而增大。随着电场强度的增大,电场力增大,导致液滴的速度和加速度增大,速度波动幅度越大[17]。同时,液滴极化状态改变越快,液滴瞬时速度波动频率越大。由图 12(b)可知,液滴平均速度随电压幅值增大而增大,这是由于介电泳力随电压幅值增大而增大。此外,由图 12(a)可知,液滴瞬时速度随着液滴靠近电极中心而增大,这是因为液滴越靠近电极中心,所受介电泳力越大。
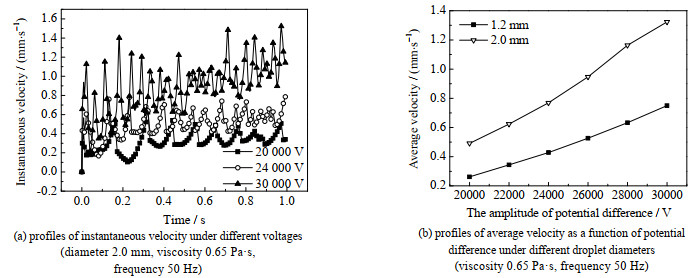
|
图 12 电压幅值对液滴迁移的影响 Fig.12 Effects of potential amplitude on droplet movement |
正弦交流电场中,液滴极化需要一定的弛豫时间,因此随着电场频率的变化,液滴极化状态随之变化。
由图 13(a)与图 12(a)对比可知,频率没有像场强那样明显地影响液滴瞬时速度波动的幅度和频率,但仍可发现液滴速度随着其靠近电极中心区域而不断增大。由图 13(b)可知,随着频率的增大,液滴平均速度先增大后减小,并在200 Hz附近取得最大值,说明存在最优频率值。在频率较低时,液滴极化充分;随着频率增大,液滴恢复时间缩短,因此能保持较强的极化状态而不减弱;但是随着频率进一步增大,液滴极化时间缩短,液滴极化程度减弱[17]。对脉冲电场中液滴变形的研究也表明存在最优频率值,随着电场频率接近该值,液滴极化程度达到最大,所受电场力达到最大,液滴变形达到最大[18]。电场中拉伸液滴变形的电场力和促使液滴迁移的介电泳力本质相同。
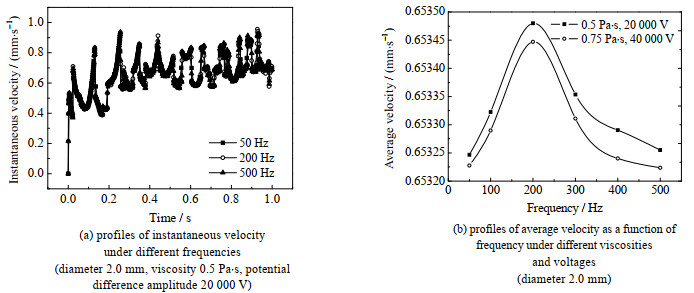
|
图 13 频率对液滴迁移的影响 Fig.13 Effects of frequency on droplet movement |
黏度是流体重要性质之一,决定了液滴受介电泳力迁移过程中的阻力[17]。
由图 14(a)可知,在不同黏度条件下,液滴速度波动的振幅和频率基本一致,这是由于黏度变化对液滴的极化状态和电场力影响微弱,并不会对液滴速度波动的振幅和频率产生显著影响。但由图 14(b)可知,随着黏度的增加,液滴整体迁移速度不断下降,这是由于液滴运动过程中所受的阻力增大,抵消了更多的介电泳力,液滴在电场中受到的合力减小,液滴的平均速度降低。在高黏度下,液滴速度小,此时由黏度增大导致的阻力增大不再明显,因此液滴速度的减小趋势也趋于平缓。
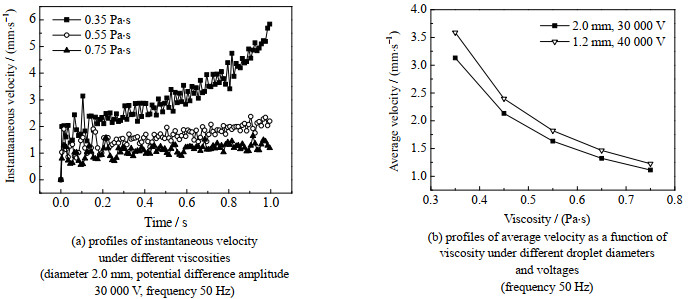
|
图 14 油相黏度对液滴迁移的影响 Fig.14 Effects of oil phase viscosity on droplet movement |
水滴粒径对介电泳的影响如图 15所示。
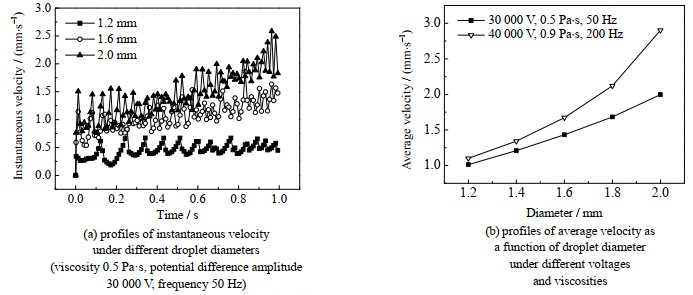
|
图 15 粒径对液滴迁移的影响 Fig.15 Effects of the droplet diameter on droplet movement |
由图 15可知,随着液滴粒径的增加,液滴迁移速度增大,这是由于积累在液滴两端的荷电量增加,液滴所受介电泳力增大导致的。因此。由图 15(a)可知,液滴瞬时速度波动幅度和频率也随粒径增大,这是由于液滴粒径增大,液滴荷电量增加,电荷对液滴表面膜的冲击性增强,液滴的变形程度增加,导致液滴瞬时速度和频率呈现更明显的周期性振荡特征,其频率接近于电场频率。由图 15(b)可知,随着粒径的增加,液滴速度呈现指数增长,这是由于介电泳力增加的速率高于阻力增加的速率,使得液滴加速度不断升高,液滴迁移速度的增速越大。
5 结论本研究基于COMSOL Multiphysics软件,通过相场方法,模拟了液滴在非均匀正弦交流电场中受介电泳力的迁移运动规律,探究了电压幅值、频率、油相黏度和液滴粒径对液滴迁移速度的影响,主要结论如下:
(1) 非均匀电场中,液滴受介电泳力向电极中心的高场强区域运动,随着液滴靠近中心,迁移速度不断增大,且由于电场强度不断变化,液滴速度呈波动变化。
(2) 在不同电压幅值和液滴粒径条件下,介电泳力占据主导地位,液滴迁移速度随电压幅值和液滴粒径的增大而增加,电压为30 000 V、粒径为2.0 mm时,液滴速度达到最大。在不同连续相黏度条件下,液滴受到的阻力占据主导,随黏度的增加,液滴迁移速度不断减小,在连续相黏度为0.75 Pa·s时,迁移速度最低接近于1 mm·s-1。
(3) 随电场频率的增大,迁移速度先增大后减小,频率为200 Hz时迁移速度最大。随着电压幅值和液滴粒径增大,液滴速度波动幅度和频率增大,而电场频率和油相黏度不会对液滴速度波动产生显著的影响。
| [1] |
MOHAMMED R A, BAILE A I, LUCHHAM P F, et al. Dewatering of crude oil emulsions[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 1994, 83(3): 261-271. |
| [2] |
SUN D, JONG S C, DUAN X D, et al. Demulsification of water-in-oil emulsion by wetting coalescence materials in stirred and packed columns[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 1999, 150(1/2/3): 69-75. |
| [3] |
TAYLOR S E. Theory and practice of electrically-enhanced phase separation of water-in-oil emulsion[J]. Transactions of the Institution of Chemical Engineers, 1996, 74(5): 526-540. |
| [4] |
HIRATO T, KOYAMA K, TANAKE T, et al. Demulsification of water-in-oil emulsion by an electrostatic coalescence method[J]. Materials Transactions, JIM, 1991, 32(3): 257-263. DOI:10.2320/matertrans1989.32.257 |
| [5] |
MHATRE S, VIVACQUA V, GHADIRI M, et al. Electrostatic phase separation: A review[J]. Chemical Engineering Research and Design, 2015, 96: 177-195. DOI:10.1016/j.cherd.2015.02.012 |
| [6] |
王贞涛, 董庆铭, 张永辉, 等. 静电场中液滴变形及内部流动的研究[J]. 高校化学工程学报, 2015, 29(5): 1098-1105. WANG Z T, DONG Q M, ZHANG Y H, et al. Droplet deformation and its internal flow in electrostatic field[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(5): 1098-1105. DOI:10.3969/j.issn.1003-9015.2015.05.011 |
| [7] |
MOHAMMADI M. Numerical and experimental study on electric field driven coalescence of binary falling droplets in oil[J]. Separation and Purification Technology, 2017, 176: 262-276. DOI:10.1016/j.seppur.2016.12.015 |
| [8] |
任瑞娟, 李彬, 孙治谦, 等. 不同电场波形下液滴极化变形规律研究[J]. 化学工程, 2018, 46(7): 51-62. REN R J, LI B, SUN Z Q, et al. Investigation on the law of droplet polarization and deformation under different electrical waveforms[J]. Chemical Engineering (China), 2018, 46(7): 51-62. DOI:10.3969/j.issn.1005-9954.2018.07.011 |
| [9] |
MHATRE S, THAOKAR R. Pin-plate electrode system for emulsion of a higher conductivity leaky dielectric liquid into a low conductivity medium[J]. Industrial and Engineering Chemical Research, 2014, 53(34): 13488-13496. DOI:10.1021/ie5017893 |
| [10] |
陈庆国, 宋春辉, 梁雯, 等. 非均匀电场下乳化油中液滴变形动力学行为[J]. 化工学报, 2014, 66(3): 955-964. CHEN Q G, SONG C H, LIANG W, et al. Kinetics behavior of water droplet deformation in emulsified oil subjected to non-uniform electric field[J]. CIESC Journal, 2014, 66(3): 955-964. |
| [11] |
陈庆国, 郑天宇, 梁雯, 等. 交流电场下液滴形变及聚结影响因素分析[J]. 电机与控制学报, 2015, 19(11): 51-58. CHEN Q G, ZHENG T Y, LIANG W, et al. Analysis of influencing factors for droplets deformation and coalescence in AC electric field[J]. Electric Machines and Control, 2015, 19(11): 51-58. |
| [12] |
陈庆国, 宋春辉, 梁雯, 等. 非均匀和均匀电场下液滴的形变及运动行为[J]. 高电压技术, 2016, 42(3): 949-958. CHEN Q, SONG C, LIANG W, et al. Deformation and motion behavior of water droplet under uniform and non-uniform electric field[J]. High Voltage Engineering, 2016, 42(3): 949-958. |
| [13] |
EOW J S, GHADIRI M, SHARIF A O, et al. Electrostatic enhancement of coalescence of water droplets in oil: A review of the current understanding[J]. Chemical Engineering Journal, 2001, 84(3): 173-192. DOI:10.1016/S1385-8947(00)00386-7 |
| [14] |
孙治谦, 周衍涛, 王振波, 等. 一种高效电脱水器: CN108949223A[P]. 2018-12-07. SUN Z Q, ZHOU Y T, WANG Z B, et al. One kind of high-efficiency electric dehydrator: CN108949223A[P]. 2018-12-07. |
| [15] |
JONES T B. Basic theory of dielectrophoresis and electrorotation[J]. IEEE Engineering in Medicine & Biology Magazine the Quarterly Magazine, 2003, 22(6): 33-42. |
| [16] |
MOLLA S H, MASLIYAH J H, BHATTACHARJEE S. Simulations of a dielectrophoretic membrane filtration process for removal of water droplets from water-in-oil emulsions[J]. Journal of Colloid and Interface Science, 2005, 287(1): 338-350. DOI:10.1016/j.jcis.2004.06.096 |
| [17] |
KAVEHPOUR H P. Coalescence of drops[J]. Annual Review of Fluid Mechanics, 2015, 47(1): 245-268. DOI:10.1146/annurev-fluid-010814-014720 |
| [18] |
LI B, VIVACQUA V, GHADIRI M, et al. Droplet deformation under pulsatile electric fields[J]. Chemical Engineering Research and Design, 2017, 127: 180-188. DOI:10.1016/j.cherd.2017.09.024 |




