2. 中国石油大学(华东)控制科学与工程学院,山东 青岛 266580
2. College of Control Science and Engineering, China University of Petroleum, Qingdao 266580, China
间歇生产方式在现代工业界所占比重越来越高,其过程监控和故障诊断也引起广泛关注[1]。长期以来,过程监控的主流统计方法[2-5]如主元分析(principal component analysis, PCA)、偏最小二乘(partial least squares, PLS)、独立元分析(independent component analysis, ICA)、典型相关分析(canonical correlation analysis, CCA)等在应用于间歇过程故障诊断时,都是采用将三维多批次历史数据展开成二维的多向(multi-way)处理方法,即使针对间歇过程的不同特点涌现出一系列改进算法[6-14],也大都对数据进行展开处理,如按批次展开、按变量展开成二维矩阵的方式等。此类多向展开的处理方法将三维多批次数据中每一批次的二维矩阵展开变成向量看待,势必会破坏原有数据的相关性,导致部分信息的丢失和特征不完全提取。
近年来,一些基于张量的数据降维方法,如张量PCA (tensor PCA, TPCA)[15-16]、张量邻域保持嵌入算法(tensor neighborhood preserving embedding, TNPE)[17]等,使用张量模式的特征提取方法对张量形式的数据进行特征提取,保证了张量形式的特征空间不被破坏,张量分析逐渐在计算机视觉、图像处理、模式识别等领域成为研究热点[18]。本文借鉴以上方法中张量分析的思想,对间歇过程在线监控时,将三维数据的每一批次看作一个二阶张量,应用TPCA算法对三维数据直接提取特征信息,不破坏三维样本中每一批次的原始矩阵空间结构,并定义R2统计量和SPE统计量建立故障检测模型;另外,为能更及时检测出间歇过程中常出现的渐变故障(如间歇精馏过程中催化剂活性的缓慢变化、间歇反应釜换热器由于长时间使用结垢现象越来越严重而导致换热性能的逐渐下降),本文利用累积和控制图(cumulative sum,CUSUM)分析思想,将其应用于TPCA算法中,提出累加和的张量主元分析(summed tensor principal component analysis, STPCA),将三维历史数据按一定的滑动窗口累加求和,累积历史信息,再做TPCA算法处理,建立故障检测模型,从而提高对渐变故障在初始出现阶段检测的灵敏度。
2 TPCA方法假设收集到的间歇过程历史数据矩阵为
| $\arg \mathop {\min }\limits_{\mathit{\boldsymbol{U}}, \mathit{\boldsymbol{V}}} \sum\limits_{m = 1}^M {\left\| {\mathit{\boldsymbol{U}}{\mathit{\boldsymbol{Y}}_m}{\mathit{\boldsymbol{V}}^{\rm{T}}} - {\mathit{\boldsymbol{X}}_m}} \right\|_{\rm{F}}^2} \\ {\rm{s.t.}}\quad {\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{U}} = I\quad {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V}} = I$ | (1) |
可通过以下迭代方法实现式(1)中U、V的求解:
Step1:初始化
Step2:设置循环变量
Step3:令
Step4:对
Step5:令
Step6:特征值分解
Step7:若
Step8:输出最终的
注意,TPCA变换处理的数据X是经过标准化处理的,其处理过程如图 1所示,第1步将初始数据
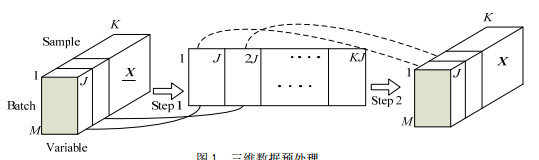
|
图 1 三维数据预处理 Fig.1 Schematic diagram of three-way dataset preprocessing |
各类间歇过程中的渐变故障很常见,渐变故障是某变量操作值缓慢偏离正常变化区间、不断累积的过程,故障初期变化量较小,很多故障检测方法对该类故障存在预报大大延迟的问题。为提高检测故障灵敏度,本文利用PAGE等[19]提出的累积和(CUSUM)控制图思想,提出一种基于累加和的张量主元分析算法(STPCA),将经过预处理后的正常批次数据
| ${\rm{summed}}\_{\mathit{\boldsymbol{x}}_m}(k) = \left\{ \begin{gathered} \sum\limits_{{k_1} = 1}^k {{\mathit{\boldsymbol{x}}_m}({k_1})} \quad \quad k \leqslant h \\ \sum\limits_{{k_1} = k - h + 1}^k {{\mathit{\boldsymbol{x}}_m}({k_1})} \quad \quad k > h \\ \end{gathered} \right.$ | (2) |
在线监控过程主要包含2个阶段。
第1阶段:离线模型的建立
① 将三维训练样本
② 对
③ 运用TPCA算法,确定投影矩阵
④ 建立故障检测模型。
对基于TPCA和STPCA 2种算法的间歇过程故障检测,本文都采用R2和SPE统计量。
R2是基于支持向量数据域描述(support vector domain description,SVDD)[20]方法建立的统计量,表示每批次
| ${{\rm{R}}^2}(m) = {\rm{tr}}({\mathit{\boldsymbol{Y}}_m}{\mathit{\boldsymbol{Y}}_m}^{\rm{T}}) - 2\sum\limits_{i = 1}^M {{\alpha _i}{\rm{tr}}({\mathit{\boldsymbol{Y}}_m}{\mathit{\boldsymbol{Y}}_i}^{\rm{T}})} + \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^M {{\alpha _i}{\alpha _j}{\rm{tr}}({\mathit{\boldsymbol{Y}}_i}{\mathit{\boldsymbol{Y}}_j}^{\rm{T}})} } $ | (3) |
拉格朗日乘子
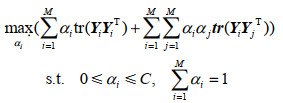
|
(4) |
SPE统计量用来测量残差空间的变化。先通过U、V重构
| ${\rm{SPE}}{_m}(k) = {\mathit{\boldsymbol{e}}_m}(k){\mathit{\boldsymbol{e}}_m}{(k)^{\rm{T}}}$ | (5) |
R2和SPE统计量皆可通过核密度估计法[22]确定各自95%或99%的置信限(也称控制限、阈值),在每个采样时刻
第2阶段:在线故障检测
① 采集新批次第
② 对预处理后的数据
③ 计算新的投影矩阵和残差:
| ${\mathit{\boldsymbol{Y}}_{{\rm{new}}, k}} = {\mathit{\boldsymbol{u}}_k}^{\rm{T}}*{\rm{summed}}\_{\mathit{\boldsymbol{x}}_{{\rm{new}}, k}}*\mathit{\boldsymbol{V}}$ | (6) |
| ${\mathit{\boldsymbol{e}}_{{\rm{new}}, k}} = {\rm{summed}}\_{\mathit{\boldsymbol{x}}_{{\rm{new}}, k}} - {\mathit{\boldsymbol{u}}_k} * {\mathit{\boldsymbol{Y}}_{{\rm{new}}, k}} * {\mathit{\boldsymbol{V}}^T}$ | (7) |
其中
④ 参考式(3)和(5)分别计算新的在线R2和SPE统计量,得到
| ${{\rm{R}}_{{\rm{new}}}}^2(k) = {\rm{tr}}({Y_{{\rm{new}}, k}}{\mathit{\boldsymbol{Y}}_{{\rm{new}}, k}}^{\rm{T}}) - 2\sum\limits_{i = 1}^M {{\alpha _i}{\rm{tr}}({Y_{{\rm{new}}, k}}{\mathit{\boldsymbol{Y}}_i}^{\rm{T}})} + \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^M {{\alpha _i}{\alpha _j}{\rm{tr}}({\mathit{\boldsymbol{Y}}_i}{\mathit{\boldsymbol{Y}}_j}^{\rm{T}})} } $ | (8) |
| ${\rm{SPE}}{_{{\rm{new}}}}(k) = {\mathit{\boldsymbol{e}}_{{\rm{new}}, k}}{\mathit{\boldsymbol{e}}_{{\rm{new}}, k}}^{\rm{T}}$ | (9) |
并判断统计量是否偏离各自阈值,以确定间歇过程运行状况。
4 仿真结果分析分批补料的盘尼西林发酵过程是典型的间歇式生产过程,本文基于BIROL等[23]开发的标准仿真软件Pensim 2.0产生的盘尼西林发酵数据进行在线监控算法仿真研究。本仿真由该软件在正常操作范围内对初始条件加入一定的微小偏移和适当噪声生成30批次数据作为训练样本,每批次含11个观测变量,反应时间相等,均为400 h,采样间隔为0.5 h,从而得到
|
|
表 1 跳变故障 Table 1 Step faults used for detection |
|
|
表 2 渐变故障 Table 2 Gradual faults used for detection |
建模时,3种方法都需要对数据进行标准化,不同的是,MPCA方法如图 1中Step 1按批次展开成二维,按列作归一化处理,得到二维矩阵
当新批次中出现故障1、2、3跳变故障时,基于MPCA的在线故障检测结果如图 2、4、6所示,MPCA的SPE统计量能准确预报故障的发生(140~300采样点),但在非故障时段有较高误报,从图中可明显看到有多点超出控制限,特别是对故障3达到了5.12%的误报率(见表 3)。相对而言,图 3、5、7所示TPCA故障检测结果中,SPE统计图既能准确检出故障,又具有较低误报率,由表 3可见,对前两个故障的误报率为0,仅对故障3有约1.63%的误报,但仍低于MPCA方法的结果。与SPE统计量相比,MPCA方法的

|
图 2 基于MPCA方法的故障1检测结果 Fig.2 Fault 1 detection results based on MPCA |

|
图 4 基于MPCA方法的故障2检测结果 Fig.4 Fault 2 detection results based on MPCA |
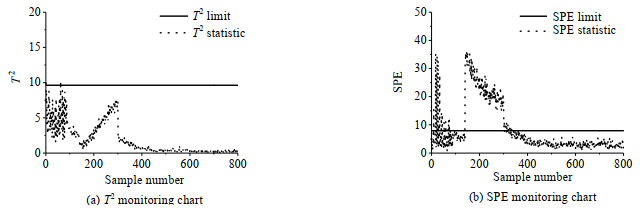
|
图 6 基于MPCA方法的故障3检测结果 Fig.6 Fault 3 detection results based on MPCA |
|
|
表 3 MPCA和TPCA方法的故障检测误报率对比 Table 3 Comparison of false positive rates (FPR) by MPCA and TPCA |
|
图 3 基于TPCA方法的故障1检测结果 Fig.3 Fault 1 detection results based on TPCA |
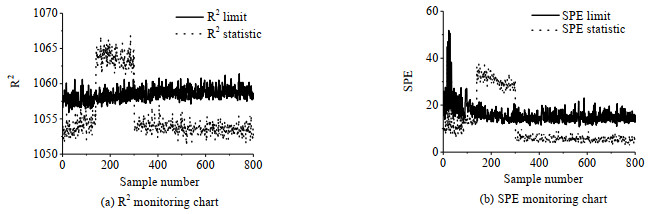
|
图 5 基于TPCA方法的故障2检测结果 Fig.5 Fault 2 detection results based on TPCA |
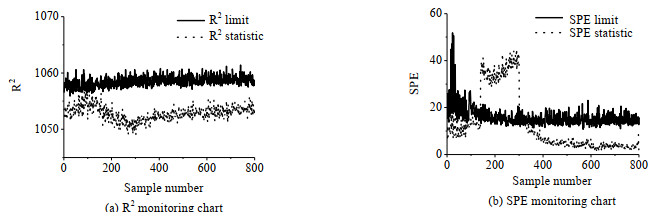
|
图 7 基于TPCA方法的故障3检测结果 Fig.7 Fault 3 detection results based on TPCA |
为提高检测渐变故障的灵敏度,本文在TPCA基础上提出基于STPCA的间歇过程故障诊断方法,同样使用R2和SPE统计图进行故障分析。仿真实验设置了表 2所述3种故障,分别是通风速率、搅拌功率、底物流加速率从第200采样点以一定速度呈现斜坡变化,模拟间歇过程中可能出现的渐变类故障。图 8到图 13反映了MPCA、STPCA方法对3个故障批次的检测效果。

|
图 8 基于MPCA方法的故障4检测结果 Fig.8 Fault 4 detection results based on MPCA |
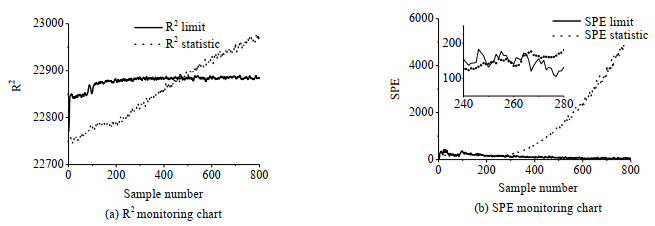
|
图 9 基于STPCA方法的故障4检测结果 Fig.9 Fault 4 detection results based on STPCA |
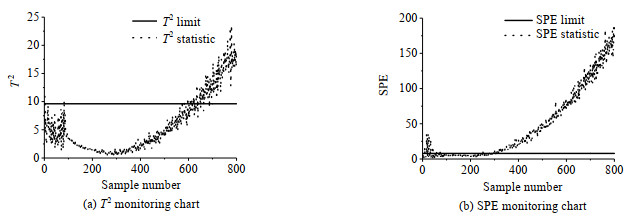
|
图 10 基于MPCA方法的故障5检测结果 Fig.10 Fault 5 detection results based on MPCA |
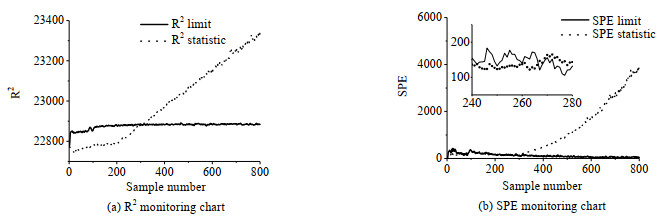
|
图 11 基于STPCA方法的故障5检测结果 Fig.11 Fault 5 detection results based on STPCA |
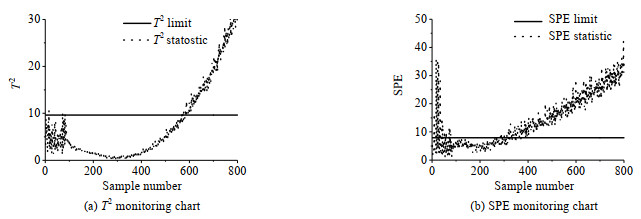
|
图 12 基于MPCA方法的故障6检测结果 Fig.12 Fault 6 detection results based on MPCA |
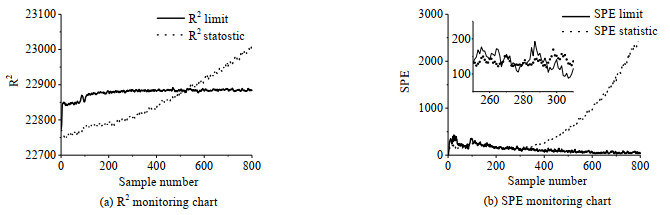
|
图 13 基于STPCA方法的故障6检测结果 Fig.13 Fault 6 detection results based on STPCA |
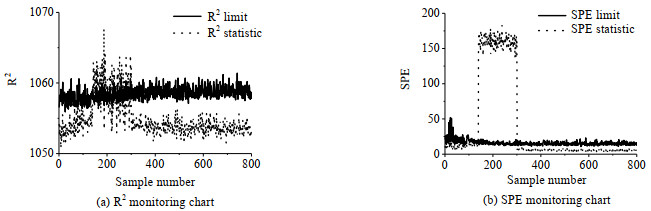
从图 8、10和12所示结果观察,MPCA的
|
|
表 4 MPCA和STPCA检出的故障发生采样点 Table 4 Fault sampling points based on MPCA and STPCA |
需要说明的是,STPCA方法更适用于渐变故障存在的场合,尤其是故障出现早期,通过CUSUM累积过程中的微小变化,提高对渐进、缓慢变化类故障初期较小故障偏移的检测。同时,该方法中累加求和宽度
传统将三维数据变成二维的间歇过程故障诊断方法,破坏数据原有的空间结构和相关特性,必然会对过程监控效果产生不利影响。本文将基于张量分解的TPCA算法引入到间歇过程监控中,直接将三维数据作为张量目标进行运算,保留了数据完整性,定义R2和SPE统计量建立故障检测模型。经仿真验证,基于TPCA的间歇过程故障诊断方法适合检测突变故障,检测效果较好。针对间歇过程中常发生的渐变故障,本文提出STPCA方法,通过对三维数据多个连续时刻的采样值求和,不断放大历史信息,同时又保证不破坏三维原始数据结构,因此在检测渐变类型故障的仿真实验中,STPCA方法有更好效果,提高故障检测灵敏度,相应降低了漏检率。
符号说明:
C —惩罚因子 summed_xm(k) —样本训练集中,累加求和处理后的第m批次第k次观测向量
em(k) —第m批次的第k个残差向量
enew, k —新的残差向量 summed_xnew, k —新批次数据中,累加求和后的第k次观测向量
h —累加求和宽度 U —Xm的左酉投影矩阵
J' —求右酉矩阵V对应保留的最大特征值个数 V —Xm的右酉投影矩阵
K' —求左酉矩阵U对应保留的最大特征值个数 Xm —第m批次二阶张量历史数据
R2(m) — R2统计量:Ym到特征空间中心的距离 Ym —Xm的低秩投影特征空间
SPEm}(k) —第m批次的第k个SPE统计量 Ymew, k —summed_xnew, k到特征空间的投影
ai —拉格朗日乘子
| [1] |
WANG R, EDGAR T F, BALDEA M, et al. A geometric method for batch data visualization, process monitoring and fault detection[J]. Journal of Process Control, 2018, 67: 197-205. DOI:10.1016/j.jprocont.2017.05.011 |
| [2] |
谢磊, 何宁, 王树青. 步进MPCA及其在间歇过程监控中的应用[J]. 高校化学工程学报, 2004, 16(5): 643-647. XIE L, HE N, WANG S Q. Step-by-step adaptive MPCA applied to an industrial batch process[J]. Journal of Chemical Engineering of Chinese Universities, 2004, 16(5): 643-647. DOI:10.3321/j.issn:1003-9015.2004.05.020 |
| [3] |
高学金, 崔久莉, 齐咏生, 等. 基于改进MPLS的间歇过程监测与故障诊断[J]. 计算机与应用化学, 2013, 30(8): 953-958. GAO X J, CUI J L, QI Y S, et al. Batch process monitoring and fault diagnosis based on improved MPLS[J]. Computers and Applied Chemistry, 2013, 30(8): 953-958. |
| [4] |
LEE J M, YOO C K, LEE I B. Statistical process monitoring with independent component analysis[J]. Journal of Process Control, 2004, 14(5): 467-485. DOI:10.1016/j.jprocont.2003.09.004 |
| [5] |
JIANG Q C, GAO F R, Hui Y, et al. Multivariate statistical monitoring of key operation units of batch process based on time-slice CCA[J]. IEEE Transactions on Control Systems Technology, 2019, 27(3): 1368-1375. DOI:10.1109/TCST.2018.2803071 |
| [6] |
WANG H G, YAO M. Fault detection of batch processes based on multivariate function kernel principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 149(1): 78-89. |
| [7] |
赵小强, 周文伟, 惠永永. 基于核熵投影的CPLS间歇过程监测及质量预测[J]. 高校化学工程学报, 2018, 32(5): 1186-1193. ZHAO X Q, ZHOU W W, HUI Y Y. Monitoring and quality prediction of CPLS batch process based on kernel entropy projection[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(5): 1186-1193. DOI:10.3969/j.issn.1003-9015.2018.05.026 |
| [8] |
DONG W W, YAO Y, GAO F R. Phase analysis and identification method for multiphase batch processes with partitioning multi-way principal component analysis (MPCA) model[J]. Chinese Journal of Chemical Engineering, 2012, 20(6): 1121-1127. DOI:10.1016/S1004-9541(12)60596-5 |
| [9] |
JIANG Q C, GAO F R, Yan X F, et al. Multi-objective two-dimensional canonical correlation analysis for successive batch process monitoring with industrial injection mold application[J]. IEEE Transactions on Control Systems Technology, 2019, 66(5): 3825-3834. |
| [10] |
常鹏, 王普, 高学金. 基于多向核熵成分分析的微生物发酵间歇过程监测研究[J]. 高校化学工程学报, 2015, 29(2): 395-399. CHANG P, WANG P, GAO X J. Batch process monitoring for microbial fermentation based on multi-way kernel entropy component analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(2): 395-399. |
| [11] |
STUBBS S, ZHANG J, MORRIS J. Bioprocess performance monitoring using multiway interval partial least squares[J]. Computer Aided Chemical Engineering, 2018, 41: 243-259. DOI:10.1016/B978-0-444-63963-9.00010-5 |
| [12] |
WANG L, SHI H B. Online batch process monitoring based on just-in-time learning and independent component analysis[J]. Journal of Donghua University (English Edition), 2016, 33(6): 944-948. |
| [13] |
TIAN X M, ZHANG X L, DENG X G, et al. Multi-way kernel independent component analysis based on feature samples for batch process monitoring[J]. Neurocomputing, 2009, 72(7): 1584-1596. |
| [14] |
张晓玲, 邓晓刚. 基于CUS-MICA的间歇过程故障诊断[J]. 控制工程, 2015, 22(6): 1207-1211. ZHANG X L, DENG X G. Fault diagnosis based on CUS-MICA for batch processes[J]. Control Engineering of China, 2015, 22(6): 1207-1211. |
| [15] |
杜博, 张乐飞, 章梦飞, 等. 基于张量主成分分析的人脸图像压缩与重构[J]. 华中科技大学学报(自然科学版), 2013, 41(12): 201-204. DU B, ZHANG L F, ZHANG M F, et al. Tensor-based principal component analysis for face image compression and reconstruction[J]. Journal Huazhong University of Science & Technology (Natural Science Edition), 2013, 41(12): 201-204. |
| [16] |
WANG X Y, YUE Y Y. 3D model classification and recognition method based on tensor principal component analysis[C]//Lisa O'Conner. 8th International Symposium on Computational Intelligence and Design. Los Alamitos: IEEE Computer Society, 2015, 1: 345-348.
|
| [17] |
LIU S, RUAN Q Q. Orthogonal tensor neighborhood preserving embedding for facial expression recognition[J]. Pattern Recognition, 2011, 44(7): 1497-1513. DOI:10.1016/j.patcog.2010.12.024 |
| [18] |
亢婉君.张量主成分分析及在图像序列识别中的应用[D].吉林: 东北电力大学, 2017. HANG W J. Tensor principal component analysis and its application in recognition of image sequences[D]. Jilin: Northeast Electric Power University, 2017. |
| [19] |
BARRATT B, ATKINSON R, ANDERSON H R, et al. Investigation into the use of the CUSUM technique in identifying changes in mean air pollution levels following introduction of a traffic management scheme[J]. Atmospheric Environment, 2007, 41(8): 1784-1791. DOI:10.1016/j.atmosenv.2006.09.052 |
| [20] |
DAVIE M J, ROBERT P W. Support vector data description[J]. Machine Learning, 2004, 54(1): 45-66. |
| [21] |
LUO L J, BAO S Y, GAO Z L, et al. Batch process monitoring with tensor global-local structure analysis[J]. Industrial & Engineering Chemistry Research, 2013, 28(5): 18031-18042. |
| [22] |
MARTIN E B, MORRIS A J. Non-parametric confidence bounds for process performance monitoring charts[J]. Process Control, 1996, 6(6): 349-358. DOI:10.1016/0959-1524(96)00010-8 |
| [23] |
BIROL G, UNDEY C, CINAR A. A modular simulation package for fed-batch fermentation:Penicillin production[J]. Computers & Chemical Engineering, 2002, 26(11): 1553-1565. |




