随着经济的快速发展,各行各业的污水排放量大增,水资源的短缺问题将更加突出[1]。空化技术是一种新兴的水处理技术,根据空化产生的方法一般可以分为超声空化、水力空化、光空化和粒子空化等4种类型。其中,水力空化是水处理研究学者关注的热点领域之一。
水力空化是指液体流经某一节流元件产生较大的压降,使得液体的压力低于其饱和蒸气压,从而发生空化的现象[2]。水力空化技术因为具有能量利用率高、装置简单、操作方便等优点[3-5],得到了广泛的应用。目前,空化发生器的主要形式有文丘里管和多孔孔板。孔板式空化器与文丘里管空化器都具有结构简单、能耗小及操作方便等优点,但空化效率还有待提高。
基于以上背景,开发新的水力空化装置具有积极的经济价值和社会效应。特斯拉阀由TESLA等[6]在1920年提出,独特的双静脉弧形设计使特斯拉阀具有与方向相关的压降特性。近些年,本课题组针对特斯拉阀进行了氢气逆向减压等多项研究。在此基础上,考虑到特斯拉阀拥有与方向相关的压降特性,形成“流体二极管”的效果,从而在逆流时可以产生较好的水力空化效果,因此在污水处理方向具有积极的应用前景。本文基于标准k-ε湍流模型,验证了特斯拉阀确实会发生空化,对不同结构参数的特斯拉阀进行数值模拟,并优化其空化效果。希望特斯拉阀可代替传统的多孔孔板和文丘里管空化器,或者与多孔孔板及文丘里管空化器配合使用,进一步提高空化效率;利用特斯拉阀多级工作的特点,在空化发生能力相差不大乃至于更佳的基础上,简化空化发生器。
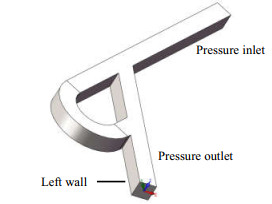
2 数值模型 2.1 物理模型利用SolidWorks进行几何建模,几何模型如图 1所示。为了保证计算域内流场充分发展,弯管处与出入口都保持一段距离。
|
图 1 几何模型 Fig.1 Geometric model |
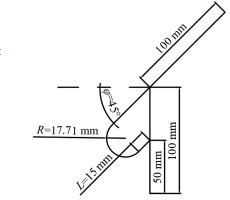
特斯拉阀的结构简图如图 2所示,其中圆弧是180°的半圆,流道截面是10 mm ×10 mm的正方形,设置如下变量:角度φ、圆的半径R、出半圆后的直流道长度L。
|
图 2 特斯拉阀结构简图 Fig.2 Structural sketch of Tesla valve |
水力空化时的流体流动可以看作液气混合流,且考虑液态水与空化泡之间相互作用的影响。所以选用流体计算软件Fluent对流场进行计算,为了研究空化,采用多相流mixture模型,两相分别为水和水蒸气,饱和蒸气压设置为30 ℃下水的饱和蒸气压4 133 Pa;采用标准κ-ε模型,模拟流体在特斯拉阀流道中的流动;采用基于压力的隐式求解器进行稳态求解;采用二阶迎风格式分别对k和ε进行差分。
2.3 边界条件和网格划分流道入口的边界条件设置为压力入口,大小为0.5 MPa;流道出口的边界条件设置为压力出口,压力为0 Pa,数值均为表压,实际压力值为表压加上101 325 Pa。如图 3所示,通过网格划分软件ICEM进行空间六面体网格划分,总网格数为40万。

|
图 3 网格 Fig.3 Mesh generation |
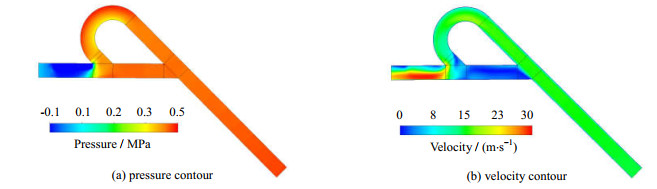
在角度为45°的情况下进行空化验证。压力云图和速度云图如图 4所示。流体从压力入口进入后在第一个分叉处分流,大部分通过弯管,小部分通过直管。在弯管出口处水流和直管水流发生冲击,产生一个很大的速度梯度,引起压力骤降。当压力梯度足够大的时候,这部分区域就会发生空化。
|
图 4 压力云图和速度云图 Fig.4 Pressure contour and velocity contour |
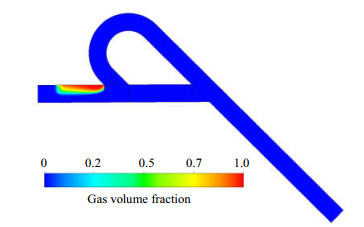
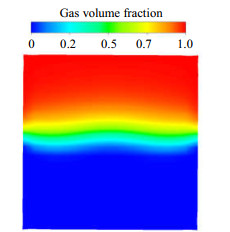
汽相体积分数云图和y=30 mm截面处汽相体积分数云图如图 5、6所示,由图可知靠近出口左壁面区域气体体积分数很高,且正方形管口截面上超过一半区域发生了空化。
|
图 5 汽相体积分数云图 Fig.5 Gas volume fraction contour |
|
图 6 y=30 mm截面处汽相体积分数云图 Fig.6 Gas volume fraction contour at y=30 mm cross-section |
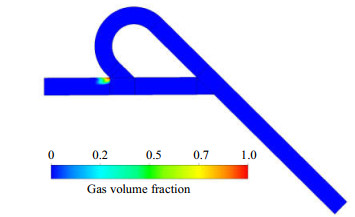
如图 7所示,当压差低于0.25 MPa时,汽含率很小,基本不发生空化;当压差高于0.25 MPa时,发生空化的区域会随着压差增大而增大。因此,进出口两端压差为0.25 MPa是发生空化的临界值。
|
图 7 0.25 MPa时汽相体积分数云图 Fig.7 Gas volume fraction contour at p=0.25 MPa |
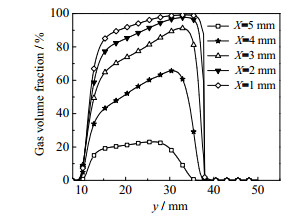
与左壁面不同距离情况下汽含率沿y轴变化曲线如图 8所示,其中X为与左壁面的距离。空化主要发生在y=10~40 mm区域内,汽含率最大值位于弯管和直管交界处区域,说明这个区域空化效果最好。越接近左壁面汽含率越高,汽含率最大值接近100%,说明有部分区域接近完全汽化,而常用的圆形孔板空化器发生空化的区域汽含率大部分在10% ~ 50%[11],由此可见特斯拉阀的空化效果优于圆形孔板。
|
图 8 与左壁面不同距离情况下汽含率沿y轴变化曲线 Fig.8 Gas volume fraction along y-axis with different distances from left wall |
湍动能强度的变化体现了特斯拉阀内部空化强度的强弱。当流场内发生空化时,空泡的产生和溃灭引起了流场的扰动,脉动压力增加,湍动能强度也相应增加。当流场远离空化区域后,湍动能逐渐降低,恢复到初始状态。
空化数是一个无量纲的常数,同样能够表示空化强度,其表达式为
汽含率也能表示空化强度。一个区域汽含率越大,说明空化强度越大。为了更好地量化空化强度,通过空化面积来比较不同情况下空化区域的大小,其中有效空化面积定义为空化长度×空化宽度。空化区域沿平行z轴方向均发生空化,空化区域体积=空化面积×10 mm。
3.3 特斯拉阀结构优化分析 3.3.1 角度对空化效果的影响如表 1所示为不同角度下截面的平均空化数。从表 1中可以看出,角度越小,平均空化数越小,而且平均空化数有随y的减小而减小的趋势,这主要是因为靠近出口处平均压力较小。此外,常用的圆形孔板空化器平均空化数为0.26[11],由表 1可知特斯拉阀在靠近出口区域空化数明显比圆形孔板的小,空化效果比圆形孔板好。
|
|
表 1 不同角度下各截面平均空化数 Table 1 Average cavitation number of sections with different angles |
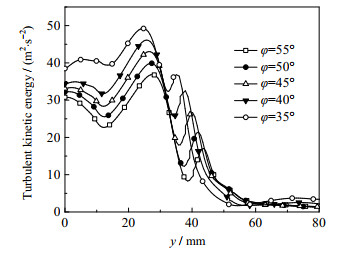
不同角度下流道中心线的湍动能强度沿y轴变化曲线如图 9所示,由图可知角度越小湍动能强度的峰值越高,空化强度越高。但事实上湍动能强度并不能完全表征空化效果,在压力出口附近流体的湍动能也处于一个较高的水平,但事实上这里并不发生空化。于是选择用有效空化面积来直观地量化空化效果,之后不再考虑湍动能强度。
|
图 9 不同角度下湍动能强度沿y轴变化曲线 Fig.9 Turbulent kinetic energy along y-axis with different angles |
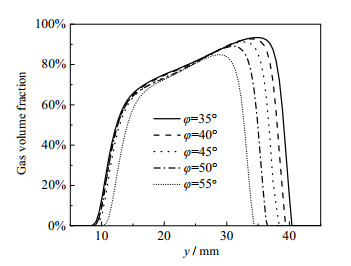
在研究角度对空化效果的影响过程中,将x=-2 mm,z=0这条空间直线上汽含率大于1%区域的长度定义为空化长度,将y=25 mm,z=0这条空间直线上汽含率大于1%区域的长度定义为空化宽度。由图 10可以看到角度越小,汽含率越高,空化强度越高,随着角度增加空化长度分别为32.32、30.81、29.80、27.78、24.24 mm。但是仿真结果显示不同角度空化宽度基本保持不变,都为6.26 mm。因此,随角度增加有效空化面积分别为202.32、192.87、186.55、173.90、151.74 mm2。总体来说角度越小,空化面积越大,空化强度越高。在本文的研究范围内,当φ=35°时,特斯拉阀内液体的空化效果最好。
|
图 10 不同角度下汽含率沿直线x= 2 mm,z=0变化曲线 Fig.10 Gas volume fraction along line x=2 mm, z=0 with different angles |
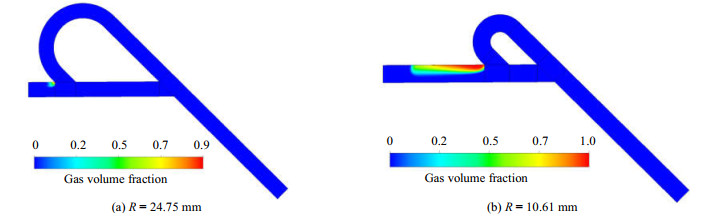
2种半径下汽相体积分数云图如图 11所示,由图可知,半径越小,空化面积越大,空化强度越高。为了量化空化效果,这里同样计算有效空化面积。空化长度还是为x=-2 mm,z=0这条空间直线上汽含率大于1%区域的长度。
|
图 11 R = 24.75 mm与R = 10.61 mm汽相体积分数云图 Fig.11 Gas volume fraction contour with R = 24.75 mm and R = 10.61 mm |
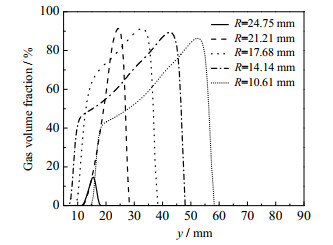
不同半径汽含率沿直线x=-2 mm,z=0变化曲线如图 12所示,按照距离从小到大排列,空化长度分别为7.07、16.67、29.80、41.41、43.69 mm。由于出口到弯管直管交界处的距离是变化的,定义空化宽度分别为y=15、25、35、45、55 mm且z=0这5条空间直线上汽含率大于1%区域的长度。距离为30 mm的情况下空化宽度为4.24 mm,其他情况空化宽度都为5.25 mm。从图 12可以看出R=24.75 mm的情况下空化强度很低,处于发生空化的临界状态。而空化宽度在空化强度达到一定值之后,基本保持不变。这里的空化宽度和改变角度得到的空化宽度数值并不相同,说明这个空化区域并不是一个矩形,不同线上宽度不同,更像是一个梯形,但方便起见还是用矩形来近似表示有效空化面积。在圆半径缩小过程中,前面一段空化长度接近线性增长,但当半径小到一定程度的时候空化长度增长趋势就开始明显减缓,立体结构的约束也让圆的半径不能过小,因此选择圆的半径为10.61 mm,此时有效空化面积最大,为229.37 mm2。
|
图 12 不同半径汽含率沿直线x = -2 mm,z = 0变化曲线 Fig.12 Gas volume fraction along line x = -2 mm, z = 0 with different radii |
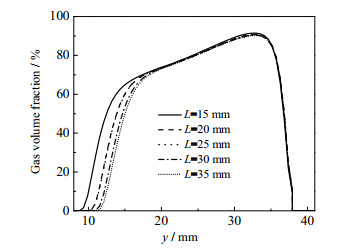
同样用有效空化面积量化空化效果。空化长度为x=-2 mm,z=0这条空间直线上汽含率大于1%区域的长度,空化宽度为y = 25 mm,z = 0这条空间直线上汽含率大于1%区域的长度。不同长度汽含率沿直线x = -2 mm,z = 0变化曲线如图 13所示,随着长度L的增加空化长度分别为29.13、27.48、27.48、26.94、26.39 mm。空化宽度基本保持不变,都为6.26 mm。由此可见出半圆后直流道长度越短,有效空化面积越大,空化效果越好。但由于空间结构的限制,长度不能太短,所以取长度L=15 mm,此时有效空化面积最大,为182.35 mm2。
|
图 13 不同长度汽含率沿直线x= -2 mm,z = 0变化曲线 Fig.13 Gas volume fraction along line x = -2 mm, z = 0 with different lengths |
本文中半径参数的修改是通过改变弯管出口与直管的交点位置实现的,上述的3个结构参数相互影响,综合优化后参数为φ=35°,R=12.28 mm,L=14.87 mm。
4 结论通过对特斯拉阀的数值模拟,发现特斯拉阀有很好的空化效果,明显优于常用的圆形孔板空化器,具有在污水处理方面应用的潜力。通过优化模型的结构参数会对空化效果产生显著影响。本文利用空化数和汽含率表征空化效果,提出运用有效空化面积量化空化效果。研究发现空化达到一定强度后空化宽度不变,故可以通过比较空化长度比较空化效果。在本文的模型里,角度φ越小、圆半径R越小、出半圆后直流道长度越小,有效空化面积越大、空化强度越高。最终优化的结构是φ =35°,R =12.28 mm,L=14.87 mm。
| [1] |
郭日生. 水资源安全保障技术发展战略研究[M]. 北京: 海洋出版社, 2007. GUO R S. Research on development strategy of water resources safety and security technology[M]. Beijing: Ocean Press, 2007. |
| [2] |
魏群, 肖波. 水力空化技术在废水处理中的研究与应用进展[J]. 中国给水排水, 2007(2): 13-16. WEI Q, XIAO B. Research and application progress of hydraulic cavitation technology in wastewater treatment[J]. China Water and Wastewater, 2007(2): 13-16. |
| [3] |
GOGATE P R. Cavitation:An auxiliary technique in wastewater treatment schemes[J]. Advances in Environmental Research, 2002, 6(3): 335-358. DOI:10.1016/S1093-0191(01)00067-3 |
| [4] |
SIVAKUMAR M, PANDIT A B. Wastewater treatment:A novel energy efficient hydrodynamic cavitational technique[J]. Ultrasonics Sonochemistry, 2002, 9(3): 123-131. |
| [5] |
KALUMUCK K M, CHAHINE G L. The use of cavitating jets to oxidize organic compounds in water[J]. ASME Journal of Fluids Engineering, 2000, 122(9): 465-470. |
| [6] |
TESLA, N. Valvular conduit: US, 1329559[P]. 1920-02-03.
|
| [7] |
QIAN J Y, WU J Y, GAO Z X, et al. Hydrogen decompression analysis by multi-stage Tesla valves for hydrogen fuel cell[J]. International Journal of Hydrogen Energy, 2019, 44(26): 13666-13674. DOI:10.1016/j.ijhydene.2019.03.235 |
| [8] |
QIAN J Y, CHEN M R, Liu X L, et al. A numerical investigation of the flow of nanofluids through a micro Tesla valve[J]. Journal of Zhejiang University-SCIENCE A, 2019, 20(1): 50-60. DOI:10.1631/jzus.A1800431 |
| [9] |
QIAN J Y, CHEN M R, GAO Z X, et al. Mach number and energy loss analysis inside multi-stage Tesla valves for hydrogen decompression[J]. Energy, 2019, 179: 647-654. DOI:10.1016/j.energy.2019.05.064 |
| [10] |
JIN Z J, GAO Z X, CHEN M R, et al. Parametric study on Tesla valve with reverse flow for hydrogen decompression[J]. International Journal of Hydrogen Energy, 2018, 43(18): 8888-8896. DOI:10.1016/j.ijhydene.2018.03.014 |
| [11] |
朱孟府, 苗秀娟, 邓橙, 等. 不同孔分布孔板的水力空化效果的数值模拟[J]. 轻工机械, 2012, 30(4): 8-11. ZHU M F, MIAO X J, DENG C, et al. Numerical simulation of hydrodynamic cavitation effect of orifice plate with different layout[J]. Light Industry Machinery, 2012, 30(4): 8-11. |
| [12] |
邓洁, 许仕荣, 张伟. 水力空化强化效应的实验研究[J]. 兰州理工大学学报, 2008(5): 78-82. DENG J, XU S R, ZHANG W. Experimental research on the enhancement effect of hydraulic cavitation[J]. Journal of Lanzhou University of Technology, 2008(5): 78-82. |




